强夯加固饱和软土地基的数值模拟方法及算例
2022-08-15左大伟
左大伟
(天津津港建设有限公司,天津 300456)
引言
强夯的设计[1-2]、试验[3-8]及实际施工过程[9-12]比较复杂,夯锤质量、夯锤直径、夯击能、夯击次数、夯坑深度、隆起高度、夯击遍数、夯锤间距、每遍时间间隔等均会影响强夯的效果,甚至很多饱和软黏土地块内需要回填杂填土,回填土厚度亦是影响因素。难以进行全程的模拟计算。但通过对理想状态下建立的物理模型进行模拟,对强夯的机理和对强夯效果的影响因素分析是有益的,本文在前人工作的基础上,结合天津沿海地区的一些具体工程地质条件进行了一些探索分析。
1 强夯的数值模拟方法
钱家欢[13]最早借助Cruse和Rizzo所获得的经过拉氏变换后的弹性体运动微分方程的基本解,用加权余量法导出弹性振动问题的边界积分方程,并将其应用于边界元解强夯问题。该方法比较老旧,目前较少采用。有研究者[14]采用FLAC3D有限差分法来评估强夯的效果。另一个流派以Biot固结理论[15-16],对强夯的过程进行模拟计算,与一般固结理论的区别是荷载非为静荷载,而是与时间有关系的冲击荷载。该理论的优点是能够考虑地基中孔隙水压力的产生和消散过程,缺点是不能考虑强夯过程中土体的动力特征。动力有限元也是比较常用的方法。该方法首先对空间域进行离散化,然后再对时间域进行离散,然后采用多场耦合进行分析。本文重新探讨这种分析方法,首先描述固体单元的动态平衡特性。
1.1 微分体的运动特征量
有限元是将研究的整体分割成有限个微分体(以下简称单元),假设微分体以速度[v]移动。则在dt时间内,第i个微分体的应变的改变量是[v]dt,相应的应变率张量表示如下

式中张量ξij表示变形速率。忽略单元所发生的转动。
1.2 运动方程和平衡方程
由动量原理的连续形式可得柯西运动方程:

1.3 本构方程
本构方程描述了土体屈服面的变化过程,其形式如下:

其中是共同转动应力率张量,[H]是给定的硬化函数,κ是考虑了加载历史的参数。
1.4 数值解法
根据初始条件和边界条件,计算过程采用以下方法来实现:
1)几何离散方法(将连续体划分为离散的单元体;所有的力(外力和重力、孔隙水压力等)都集中在三维网格的结点上。
2)时间离散方法采用有限差分方法(一个变量的空间和时间的微分由有限差分去逼近,假定变量在有限空间和时间间隔内的变化是线性的);
3)动态求解方法(动态方程中的惯性量作为系统达到平衡状态时的数值量度)。
这样一般的微分方程就可以及时运用显式有限差分方法求解。
1.5 应变率计算
根据上一步计算得到的速度场,有限差分方程得出单元中每一个微分体的应变率张量的分量。
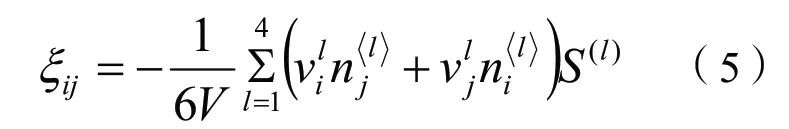
式中V为单元体的体积;上标l表示该单元体作用的总和;n为法线向量;S为微分体的总面积。运用混合离散技术,可知
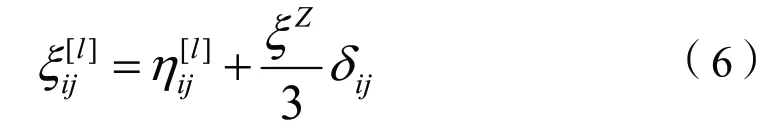
假定ξZ是单元的第一应变率不变量的平均值

nt是参与计算的单元的总数,V[k]是编号为k的单元体的体积。
1.6 应力计算
本构方程的增量形式H*ij用来计算单元中每个微分体的应力增量:

其中
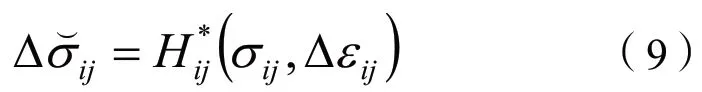
应变用下式计算

即可求得新的应力。
运用混合离散技术,调整应力张量分量的对角线分量:

且

1.7 节点不平衡力计算
在节点l处,与该节点相连的四面体对该节点的不平衡力的贡献是应力和体力两方面得到的

该点总的不平衡力就是将所有与该点相连的四面体对该点的不平衡离相加。如果必要的话用两种离散所得平均值。所加外荷载在该点的贡献[P]<l>和集中荷载相加,得到节点处的不平衡力:

2 流固耦合
2.1 基本概念
根据式(14)计算的各单元节点的不平衡力,根据土力学的原理计算由强夯引起的节点孔隙水压力,然后根据固结理论计算孔压的消散过程。在软土的强夯过程中,应该考虑土体渗透系数和其他土性指标的变化。
2.2 数学描述
假定土体饱和。根据平衡方程及达西定律,形成差分方程,该差分方程在给定几何形状,属性,边界条件以及初始条件以后即可求解。
1)规定及定义
xi、ui、vi和(dvi/dt)i=1,3分别代表介质中一点的位置、位移、速度和加速度。爱因斯坦求和约定只实用于下标i、j、k,取值范围是1,2,3。假定Lc=流域的体积/流域的面积,定义流体扩散率c:
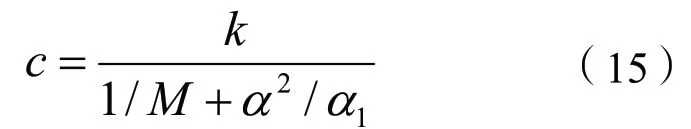
其中k是表观渗透系数,比奥模数M=kf/n,a是比奥系数,a=K+4/3G,K是排水体积模量,G是剪切模量。
2)流动方程
a)渗流的运动规律:
流体的运动用达西定律来描述。对均匀的各向同性的固体和密度为常数的流体,达西定律的形式如下:

b)体积平衡假定:
对小变形问题,流体质量守恒可以表述如下
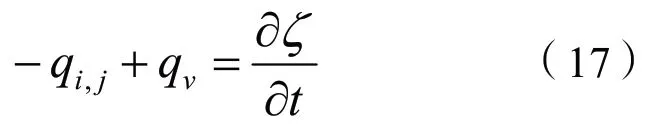
其中qv是体积流体源强度[1/s],ζ是单位体积的多孔介质中流体体积的改变量。
3)初始条件和边界条件
初始条件对应已知的孔压和饱和度与上一次的计算结果有关。渗透性边界的表达符合达西定律:

其中qn=边界外发线方向上的比流量;
h=表观渗透系数,每一级强夯应根据固结情况取不同值;
p=边界处的孔压;
pe=引起渗流的孔压。
3 数值解法过程
3.1 基本假定
耦合流体力学静态模拟涉及一系列步骤,每一步都包含一个或多个流动步,由足够多的力学平衡步跟随从而保持准静态平衡。
由于流动引起的孔压的改变是在流动步中计算,而体应变引起的孔压的改变则在力学计算步中计算。(该值是一个针对单元的值,然后分配到各个节点)。对有效应力计算,由体应变引起的孔压改变而导致的总应力增量在力学平衡步中计算,由流体流动引起的则在流动步中计算。
对于一个演员来讲,塑造良好的身体形态是非常重要的。演员可以通过运动,如慢跑、游泳来增强身体的协调性,这有助于演员在表演的时候表现得轻盈、灵活。良好的身体形态还能够使人变得自信,有助于唱歌发声,塑造一个完美的舞台形象。通过不同的身体姿态能够表现出不同的美,有的声乐演唱要表现得端庄、典雅,有的则需要表现出轻盈、灵活。通过身体姿态的变换,向观众传达出不同的情感、不同的美感,或潇洒豪放,或秀丽甜美。值得注意的是,无论作品本身要表现的情感是悲伤还是愉快,演员本身都要表现出一种庄重的气质,不能够使身体松懈,从而影响表演。
3.2 时间步长的确定
显式有限差分必须保证时间步小于某个限定值才能保证数值上的稳定。这个限定值就是特征时间步
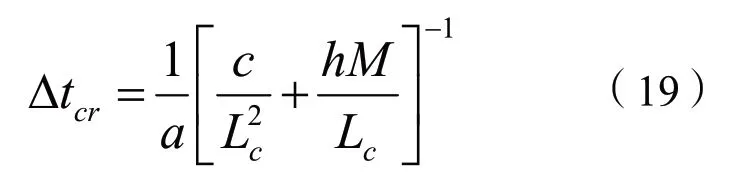
其中c是流体扩散度,a是大于1的常数,取决于几何离散方法。例如,当单元为立方体时a=6。
4 强夯数值模拟分析
4.1 建模过程
1)计算参数的选取
计算中土体采用摩尔库仑模型,夯锤用线弹性模型。土体物理力学参数及夯锤物理力学参数如图1所示。
2)有限差分网格的刨分见图1。土体尺寸为10 m×10 m×12 m,为满足波的传播需要,单元最大尺寸应该有上限,据此各个方向单元个数分别取为19、19、12。

图1 有限差分网格的刨分
3)计算分三步进行
包括自应力平衡;加入地下水(与地表齐平);及施加桩体冲击荷载。(选取局部阻尼作为动力计算中的力学阻尼,阻尼系数取0.125。)
在前两个步骤计算中,除上表面是自由面外其余各面都采用固定约束。在第三步动力计算时模型采用了粘滞性边界和自由场边界来降低人工边界对计算结果的影响。
4)计算结果及结果分析
图2、图3展示的是计算到5秒时孔压和土体竖向位移云图。由图可见,对计算采用的这种土,负孔压出现在夯锤附近一定范围内。从位移云图上可以清晰看见夯击作用力对土体的影响深达3.8 m左右。

图2 孔压分布云图

图3 竖向变形图
图4记录了从中心对称轴到边界区域的跟踪点的孔压随时间变化曲线,如图所示,最大正孔压随距夯锤中心的横向距离增大而减小。可以观测到,由于夯锤作用,地表产生较大正孔压,在短时间内快速消散,并在靠近夯锤中心位置产生了较大负孔压,经历较长时间消散。


图4 落锤附近区域孔压消散曲线
在横向,离夯锤中心点1.84 m之内,正孔压的最大值变化比较快,1.84 m以外趋于平缓;而负孔压绝对值的最大值则是在0.79 m处达到最大值。在纵向,由于受静水压力初始值的影响,曲线基本呈一平缓直线,只是在地表以下1.5 m的地方有个突起;负孔压绝对值的最大值则是在1.5 m以上随着深度加深呈直线下降,但在1.5 m以下就没有出现负孔压。
4.2 参数分析
本节主要考虑渗透系数、落距和土体弹性模量对土体孔压响应的影响。分析中为确定单因素的影响,因此研究中固定其他项,只改变单一变量分析其对结果的影响。
图5为不同渗透性(渗透速度为0.0001 cm/s、0.001 cm/s、0.01 cm/s、0.1 cm/s、1 cm/s)对落锤区域孔压消散曲线的影响。可以看到,渗透系数对最大正孔压和最大负孔压的数值没有影响。渗透系数对消散过程起决定性影响。当渗透速度在0.01~1 cm/s范围内,孔压消散速度受渗透性影响明显;而当渗透速度在0.0001~0.001 cm/s,曲线受渗透性影响较小。
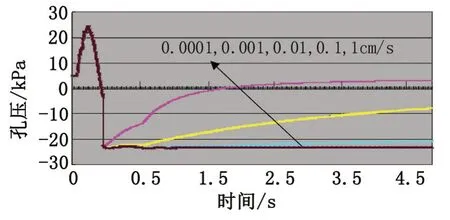
图5 渗透性对孔压消散曲线的影响
图6主要考虑落距的大小对孔压数值大小的影响。落距大小对最大正孔压影响不明显,对最大负孔压影响较为明显。当落距在一定范围内变化时,落距对孔压消散速度没有影响。

图6 落距对孔压消散曲线的影响
图7主要考量不同土体弹模对孔压变化的影响弹模越小,在落距相同的夯锤作用下土体产生的最大正孔压和最大负孔压数值越大。同时,弹模越小,在此基础上改变弹模量值对结果影响较大。
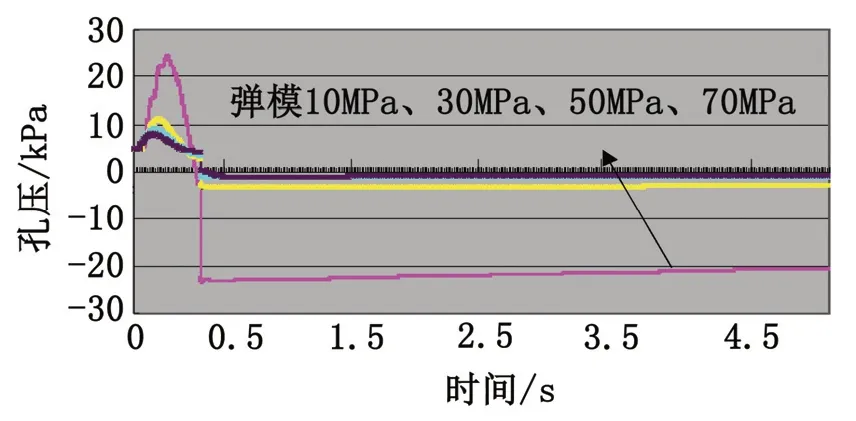
图7 土体弹模对孔压消散曲线的影响
5 工程实例
本文考虑天津港某工程的情况,地表有2 m左右的碎石层,下面为淤泥层、细砂层和边界土层,如图8所示。夯锤模型与前述相同
5.1 建模过程
计算参数选择如图8所示。边界条件设置如前节所述,地下水位先设置在地表。

图8 有限差分网格的刨分
5.2 结果分析
天津港某工程中分层土在夯锤作用下的孔压曲线,在成层土夯锤作用下随着土体分布呈差异性响应:
1)细砂层中没有负孔压出现,孔压震荡幅度的最大和最小值都是在夯锤中心的土体单元中,随着横向距离不断增大,孔压幅值逐渐减小;
2)淤泥层中离夯锤较近处有负孔压出现,较远处(1.2m)没有负孔压产生,孔压的震荡幅值随距离夯锤的间距增大而减小;
3)夯锤底部纵向不同位置处,淤泥层中的孔压震荡幅值最大,且有负孔压,而在细砂层中没有负孔压。在表层碎石层中离夯锤较近处有负孔压出现,较深处没有。
6 结语
本文通过理论分析、数值模型并与工程实例计算相结合的方法,对天津地区强夯加固饱和土体进行了动力条件下的耦合固结数值模拟。着重分析了强夯条件下孔压的影响区域范围及消散曲线,并考量了强夯实施过程中,表层土体渗透性、落距及土体弹性模量对土体中孔压消散曲线的影响。本文最后结合天津港某工程地质条件论述了强夯工程中土层分布对孔压及消散规律的影响。
