基于精密单点定位获取CGCS2000坐标方法研究
2022-08-15王志文雷力军
王志文,雷力军
(中交第一航务工程勘察设计院有限公司,天津 300220)
关键字:CGCS2000坐标;精密单点定位;ITRF
引言
2000国家大地坐标系(CGCS2000)自2008年开始推广实行,目前港口工程测量有时会要求提供2000国家大地坐标系的测量成果,但有一些地区暂无2000国家大地坐标控制点成果,这种情况下一般会采用千寻或CORS进行2000国家大地坐标系的测量工作。由于没有2000国家大地坐标系的控制点,在使用千寻或CORS进行测量时没办法进行定位校核,导致测量校核资料不完备,存在一定质量安全隐患。
精密单点定位(PPP)是一种新型的GPS定位方法,具有其他技术无法比拟的优势,只使用一个GNSS接收机即可获取厘米级的定位结果[1]。PPP技术为解决上述难题提供了契机,在无2000国家大地坐标成果区域进行测量时可采用PPP解算出某点位的2000国家大地坐标,再与千寻或CORS的测量结果进行对比,保证了测量过程的资料完备性以及保障了测量的精度和质量。本文通过具体的工程实例来梳理PPP技术在获取2000国家大地坐标的流程以及研究能达到的定位精度。
1 PPP基本原理和方法
PPP基于事后高精度的精密轨道、钟差、ERP等数据产品结合外业采集的非差伪距和载波观测数据进行定位解算。解算过程中对定位精度有影响的参数进行模型改正,把无法模型化的参数带入解算矩阵中进行参数估计。因此定位模型的优劣直接影响着定位精度。
PPP的定位模型可分为函数模型与随机模型,分别表征预估参数与观测量的关系以及观测值统计信息[1]。
1.1 PPP函数模型
载波相位和测码伪距是PPP中主要的两种原始观测量。PPP基本观测方程的搭建将依据于待估参数与GNSS观测量间的关系,并考虑各种模型化误差。由于电离层延迟误差是与频率相关的误差,其不同的处理策略将对应不同的PPP定位函数模型[2]。
GNSS非差载波相位和伪距基本观测方程为:
λj为波长(m);
Br,Pj,为接收机端伪距硬件延迟偏差,卫星端的伪距硬件延迟偏差(m);
Br,Lj,为接收机端相位硬件延迟偏差,卫星端的相位硬件延迟偏差(m);
εPj,εPLj为伪距和载波未模型化误差(多路径,噪声)。
相关模型误差可通过模型来改正,如可通过IERS conventions 2010进行海洋潮汐、地球固体潮与极潮改正,可通过IGS08模型进行天线相位中心改正。
1.2 PPP随机模型
在进行PPP构建模型时不仅仅需要考虑函数模型,还需考虑随机模型,随机模型是根据数据自身精度、系统的变化特征等条件来进行改变。在PPP中采用较多的随机模型为信噪比模型和高度角模型[3,4]。
1)高度角模型
高度角模型是将卫星高度角E和测量噪声σ构建函数关系式,通用公式如下:

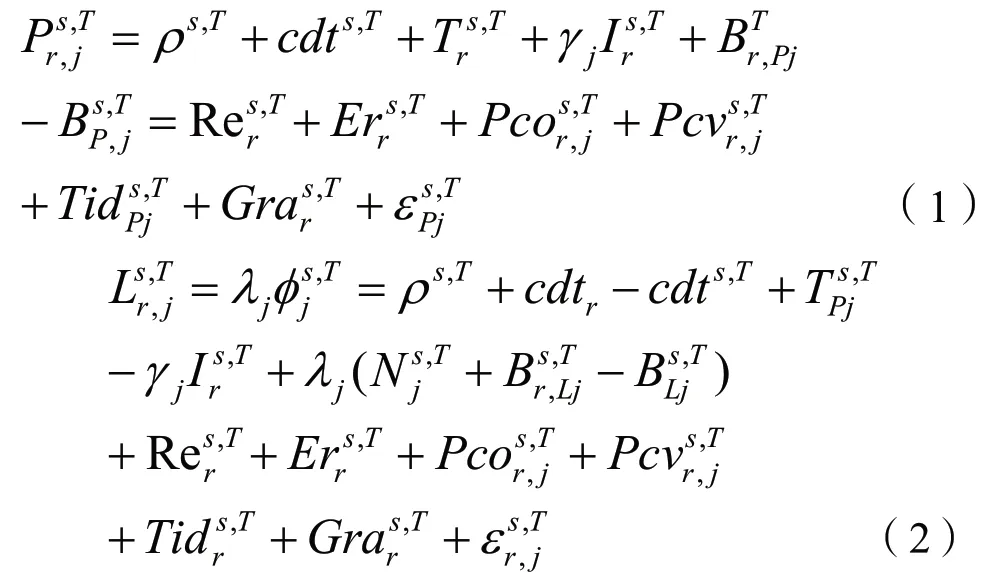
式中:
下标r和上标S分别指代接收机和卫星;
下标j表示频率;
T表示卫星系统;
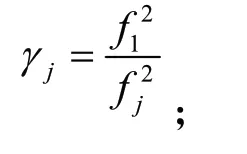
ρs为卫星至接收机的几何距离(m);
C为真空光速(m/s);
dtr,dts为接收机钟差和卫星钟差(m/s);
Is为第一频率的电离层延迟(m);
其中为正余弦函数,应用较为广泛,为许多知名的测量数据处理软件使用。比如GAMIT软件高度角模型采用的是正弦函数,即:
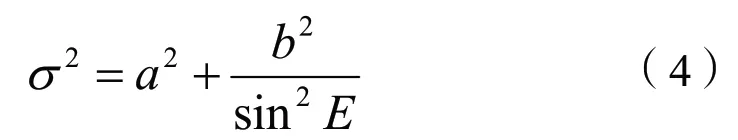
Bernese软件是余弦函数,即:
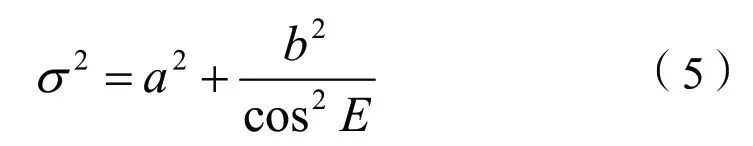
式中,和b是常数。
2)信噪比模型
信噪比模型是根据观测噪声建立随机模型,通常信噪比可反映观测数据质量好坏。载波相位观测值的SIGMA-δ随机模型为:
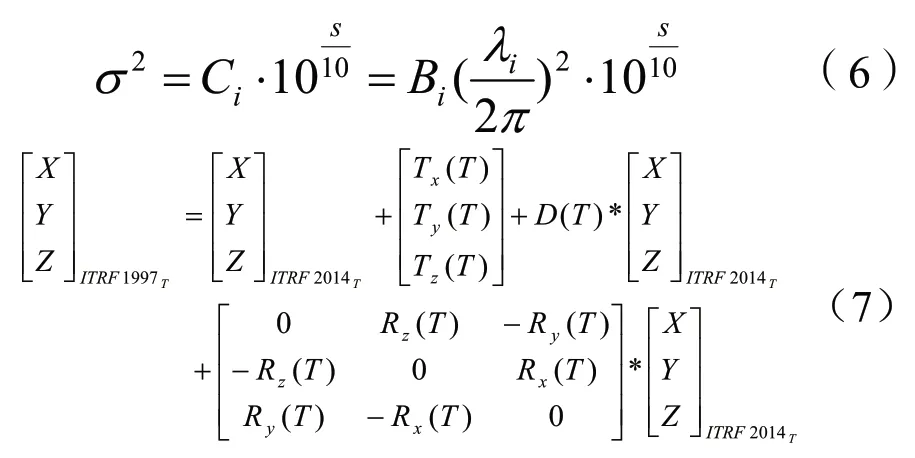
式中:
Bi表示相位跟踪环带宽(Hz);
S是信噪比;
λi是对应的波长;
C1=0.00224m2Hz;
C2=0.00077m2Hz。
2 PPP获取2000国家大地坐标的原理
2.1 数据准备
1)数据采集
将GNSS接收机放置在待求坐标的点位上,以静态作业模式进行野外数据采集。
2)事后高精度GNSS产品下载
通过IGS(International GNSS Service)等相关网站下载事后精密卫星轨道、钟差等相关数据产品[5]。
2.2 精密单点定位解算
相关数据准备完后,将外业采集的数据和下载的相关数据导入PPP解算软件中,使用PPP解算软件进行定位解算。因下载的精密轨道的坐标为ITRF2014框架下的坐标,在PPP解算时会把卫星坐标进行强约束来解算站点坐标,故PPP解算的坐标成果与精密轨道坐标系统一致,为ITRF2014框架下的坐标。2000国家大地坐标系是ITRF1997框架在2000.0历元的坐标。因此PPP软件解算后的坐标还需进行框架、历元转换才能最终得到2000国家大地坐标[6]。
2.3 框架、历元转换
1)不同框架间的转换
不同ITRF框架可采用7参数及其变化速率进行转换。具体转换参数可从ITRF官网下载获取,ITRF1997与2014的具体转换参数可见表1、表2所示[7]。

表1 转换七参数

表2 转换七参数速率
在获取框架之间的转换参数后可根据式(7)实现两框架在T历元下的转换。T历元下的七参数值可根据表1中的数据计算获取。
2)同一框架下不同历元间转换
由于受到地壳、板块运动的影响,测站位置并非固定不变,而是随着地壳的运动发生变化,这是进行同一框架内不同历元间坐标转换的原因[7]。同一框架内不同历元间坐标转换就是根据站点坐标的移动速度来实现的,具体转换见式(8)所示:

框架点的站坐标的移动速度可以从ITRF发布的SINEX文件中获取,但现实工作中测量的站点并非框架点,故只能采用欧拉公式获取站点坐标速度[8],具体公式可表达如下:
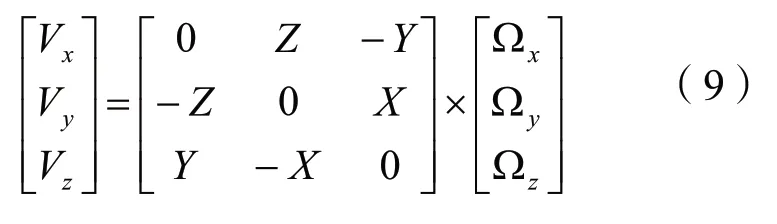
式(9)中:Vx、Vy、Vz表示站点的站速度;X、Y、Z表示站点的坐标;Ωx、Ωy、Ωz表示欧拉矢量。
根据公式(9)最少采用3个ITRF框架点利用最小二乘平差法可以解算出3个欧拉矢量。然后再将计算站点的坐标和解算的欧拉参数带入式(9)即可获取计算站点在ITRF框架下的坐标变化速度。
3 实例计算
我司接受了阳江港吉树作业区控制测量任务,要求提供2000国家大地坐标成果,由于我司掌握了当地2000国家大地坐标控制点A、B、C(假定站名)。故在上述3个2000国家大地控制点上架设GNSS接收机,分别采集了时长达6小时的观测数据,使用PPP技术进行2000国家大地坐标解算并与已知坐标成果进行对比,来探究PPP解算2000国家大地坐标的精度以及可行性。
3.1 数据准备和解算
从IGS上下载了与观测时间一致的精密轨道、精密钟差、ERP等相关数据产品,然后将所有数据导入PPP解算软件当中进行坐标解算,具体结果见图1所示。
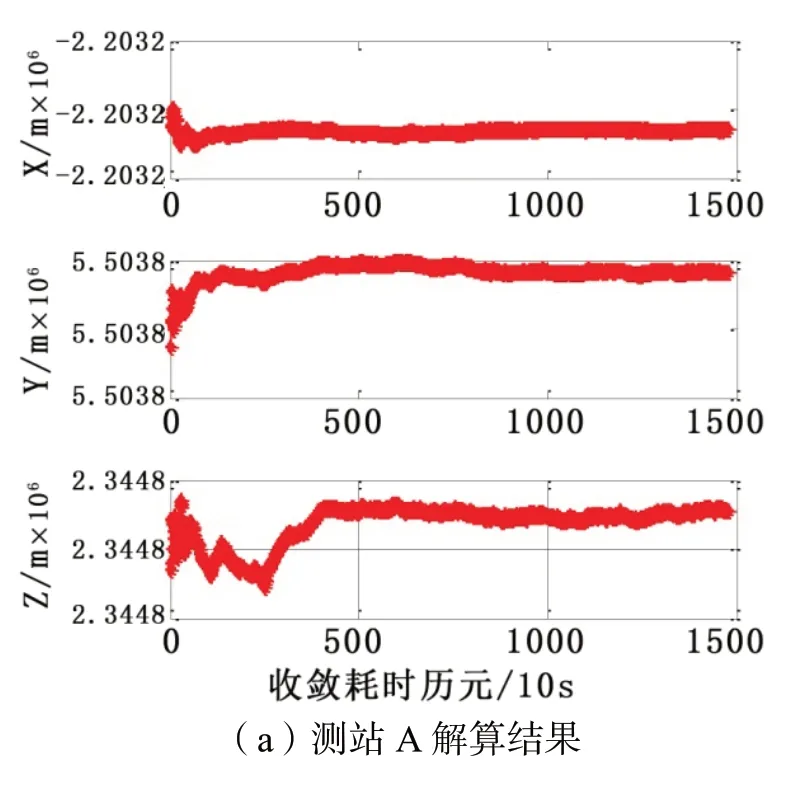
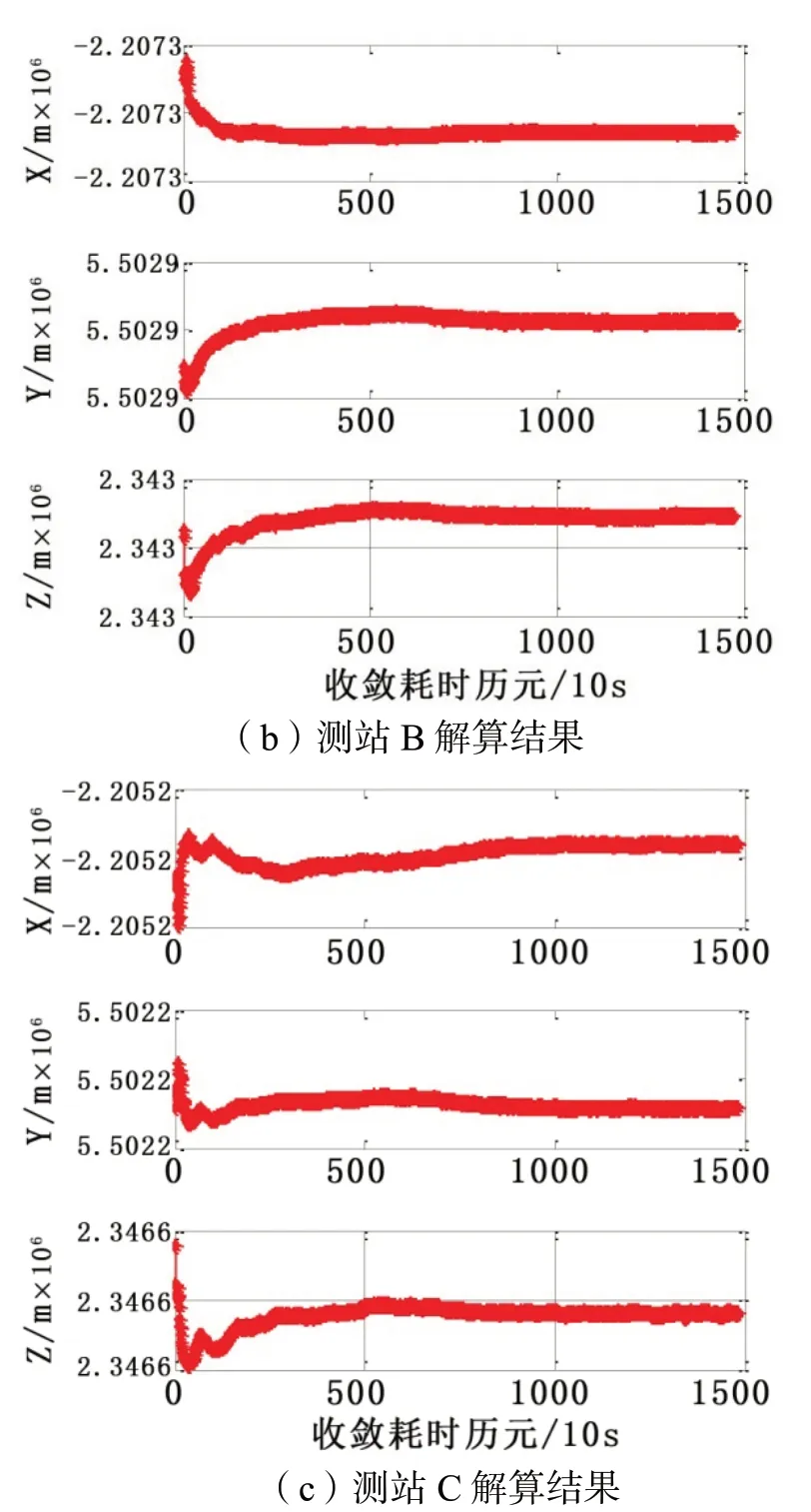
图1 PPP解算结果
注意的是PPP直接解算后的坐标为采集数据段中间时刻下的ITRF2014坐标(空间直角坐标)。
3.2 历元转换
该三个站点并非框架站点,只能采用公式(2)求解站点坐标的变化速度。从ITRF发布的SINEX文件中选出了3个位于中国的框架点WUHN、CHAN、XIAN,该三个站点的全球分布情况见图2所示。将测站数据带入到式(3)中,经最小二乘准则解算出三个欧拉角,再将解算的欧拉角以及PPP软件解算出的测站坐标一起带入到式(3)即可获取测站的站速度,由于测站A、B、C相距相对较近(三个测站间距在3~5km范围内),导致解算的站速度相同。
图2 站点全球分布情况
解算出站速度后,可根据公式(2)实现坐标在同一框架下的历元转换,将观测时刻的2014框架坐标转换到2000.0历元下。历元转换前后坐标差见图3所示。通过图3可以看出历元转换对2000国家大地坐标解算尤为重要,其影响程度可达分米级。
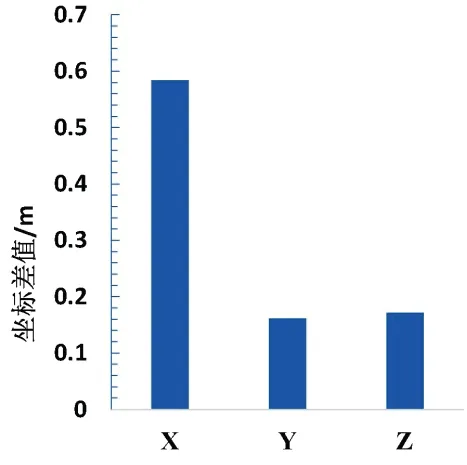
图3 历元转换前后坐标差
3.3 不同框架之间的转换
2000国家大地坐标为2000.0历元的ITRF1997坐标。因此想要最终获取2000国家大地坐标,需要将经过历元转换后的ITRF2014框架坐标转换到ITR1997框架。根据表1可以计算出2000.0历元时的转换参数并带入式(1)实现框架的转换。
框架转换前后坐标差见表2所示,通过表2可以看出框架转换对2000国家大地坐标的影响程度为厘米级。
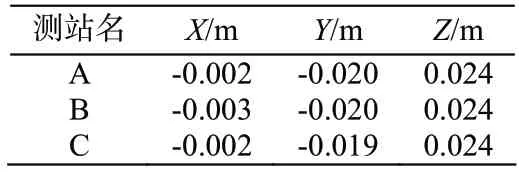
表2 框架转换前后坐标差
3.4 结果检验
将PPP解算的坐标经过同一框架不同历元之间的转换、同一历元不同框架之间的转换之后可以获取2000国家大地坐标(空间直角坐标),将解算的空间直角坐标经过地图投影获取平面直角坐标,将平面直角坐标与广东省国土资源测绘院提供的已知坐标做差来检验基于PPP方法解算的2000国家大地坐标精度如何,具体结果可见表3所示。

表3 解算的2000国家大地坐标与已知坐标做差
由表3可知,基于PPP方法解算的2000国家大地坐标精度可达厘米级,证明基于该方法可以获取高精度的2000国家大地坐标,能够满足日常测量精度的需要。
4 结语
本项目依托具体实例对基于PPP技术获取2000国家大地坐标的方法进行研究,将PPP解算流程和所需数据以及PPP解算的ITRF2014框架下的坐标到ITRF1997框架2000.0历元下的坐标的转换过程进行系统梳理,通过实际数据解算验证了基于该方法解算的2000国家大地坐标可达厘米级,能够满足日常测量的需求。
