变形温度与应变速率耦合作用对TWIP效应Ti-15Mo合金力学性能的影响
2022-08-15闵小华
姚 凯,闵小华
(大连理工大学 材料科学与工程学院,辽宁 大连 116024)
体心立方(BCC)结构的亚稳β型钛合金具有塑性变形多样性,比如应力诱发α′/α″马氏体和ω相变、应力诱发{332}〈113〉和{112}〈111〉孪生以及位错滑移,为较大范围内调控合金的强塑性提供可能[1-3]。变形方式依赖于β相稳定性,具有低β相稳定性的合金主要通过应力诱发α″马氏体和{332}〈113〉孪生变形,具有显著的应变硬化效应,称为相变诱发塑性(transformation induced plasticity,TRIP)和孪生诱发塑性(twinning-induced plasticity,TWIP)效应[4-5]。近年来,国内外学者通过d-电子合金设计理论和Mo当量等经验参数开发出诸多具有TRIP/TWIP效应的亚稳β型钛合金[6-10]。此外,时效过程中析出的ω和α相会导致合金元素的重新分布,引起变形方式的改变[11-12]。上述研究主要集中在室温及低应变速率(10-4s-1或10-3s-1)下,然而该类合金在服役过程中可能遭受高温及高应变速率,其在复杂变形条件下的变形行为依然缺乏系统的认识。近年来,人们在变形温度对亚稳β型合金变形方式和力学性能影响方面开展了一些研究工作。Zhan等[13]发现,随变形温度由293 K升高至873 K,Ti-25Nb-3Zr-2Sn合金的屈服强度呈现出先升高后降低的趋势,而其抗拉强度和加工硬化率单调降低。Yao等[14]发现,Ti-15Mo合金的屈服强度在298~673 K拉伸时基本保持不变,这不同于一般金属材料的屈服强度随变形温度的升高而逐渐降低的规律;而其均匀伸长率和加工硬化率均随变形温度的升高而降低。变形温度的升高导致ω相析出,使得β相稳定性升高,引起变形方式由{332}〈113〉孪生转变为位错滑移。这一方面补偿了由于温度升高导致的屈服强度的降低,另一方面,{332}〈113〉孪生的抑制减弱了动态Hall-Petch效应,导致加工硬化率的降低。因此,不同于变形温度对金属材料力学性能的影响只取决于位错热激活行为,变形温度对具有多变形方式的β型钛合金力学性能的影响还依赖于变形方式的转变。同样地,国内外的一些研究者调查了应变速率对变形方式和力学性能的影响。陈威等[15]发现,Ti-10V-2Fe-3Al合金中诱发α″马氏体相变的门槛应力随应变速率的增加逐渐增大。Ji等[16]发现,Ti-10Mo-1Fe合金的屈服强度随应变速率的增加逐渐升高,而其抗拉强度、均匀伸长率及加工硬化率均逐渐降低,呈现出负的应变速率敏感性。高应变速率下绝热效应引起的温度升高使得β相稳定性升高,抑制{332}〈113〉孪晶的产生。然而,Zhan等[17]发现,Ti-25Nb-3Zr-3Mo-Sn合金在10-3~103s-1应变速率范围内均通过{332}〈113〉孪生变形,其力学性能未发生明显变化。在Ti-10V-3Fe-3Al-0.27O合金中,Ahmed等[18]发现,随应变速率增加,其由应力诱发α″马氏体相变转变为{332}〈113〉孪生,使得合金的屈服强度和抗拉强度均逐渐升高,而均匀伸长率降低。Zhao等[19]提出多尺度位错模型,从理论上预测TWIP效应钛合金流变应力的应变速率依赖性,并指出相稳定性对孪生动力学的影响规律。由此可见,应变速率对具有TWIP效应的β型钛合金力学性能的影响也主要取决于变形方式的转变。
可见,变形温度和应变速率均影响β型钛合金的力学性能,并且其影响不同于一般金属材料只取决于位错热激活行为,其影响均关联塑性变形过程中变形方式的变化。此外,变形温度和应变速率耦合作用对其力学性能的影响规律尚不明确,在一定程度上限制了β型钛合金在复杂服役环境下的应用。本工作采用TEM,EBSD,SEM,XRD,OM等方法研究变形温度和应变速率耦合作用对{332}〈113〉孪生诱发塑性效应Ti-15Mo合金力学性能的影响。探讨变形温度和应变速率耦合作用对该合金力学性能的影响规律,并通过构建流变应力模型进一步探讨上述因素耦合作用对变形组织以及应变硬化行为的影响机理。
1 实验材料与方法
1.1 实验材料制备
利用冷坩埚悬浮熔炼制备Ti-15Mo合金铸锭1.0 kg。将其在1273 K下均匀化处理60 min,并在此温度下热锻成尺寸为90 mm(l)×40 mm(w)×40 mm(t)的块体。在1173 K下,将上述块体进行多道次孔型轧制成横截面为200 mm2的棒材后空冷[14]。从棒材上切取长度为60 mm的长棒,在1173 K下固溶处理(solution treatment,ST)60 min,水冷。棒材的轧制方向定义为RD(rolling direction),轧制最后一道的主应力方向定义为ND(normal direction),同时垂直于RD和ND方向定义为TD(transverse direction)。此外,将上述ST后的Ti-15Mo合金于573 K下保温10 min后水冷,定义为STA试样。
1.2 力学性能测试
将ST试样加工成总长度为60 mm的狗骨头状拉伸试样,平行段长度和直径分别为16 mm和3.5 mm。利用Instron5581型拉伸试验机,在298 K和573 K下进行拉伸速度分别为0.5,5,50,500 mm/min的单轴拉伸实验(对应的应变速率分别为5.21×10-4,5.21×10-3,5.21×10-2,5.21×10-1s-1)。573K下的拉伸实验具体操作如下:将炉温设定为573 K,待其达到实验温度后迅速将拉伸试样置于炉中;待炉温重新升至573 K(时间约为8 min)后开始拉伸实验。
1.3 变形组织表征
使用线切割从拉断试样中距断口12 mm处切取试样,并镶嵌在胶木粉中。利用金刚石抛光液以及SiO2和H2O2混合液抛光成镜面。随后在由H2O,HNO3和HF组成的腐蚀液中腐蚀1 min。采用VHX-600型光学显微镜(OM)对变形组织进行观察,利用Image-J图像分析软件对采集得到的金相照片进行处理,计算得到孪晶面积分数;利用配备有取向分析系统(HKL)的场发射扫描电镜(FESEM)进行背散射电子衍射(EBSD)分析,扫描步长为1.5 μm;利用FESEM对各变形温度和应变速率下的拉伸断口进行观察,并基于线截法统计韧窝直径;利用Rigaku TTR Ⅲ型X射线衍射仪对试样进行XRD分析,所用靶材为Cu靶,管电压和管电流分别为40 kV和150 mA,扫描角度为30°~130°,扫描速度和步长分别为1 (°)/min和0.01°;依据修正的瓦伦-艾弗巴赫法[16]计算得到位错密度。将ST和STA试样打磨至厚度为50 μm后,利用冲压器制备直径为φ3 mm的圆片。随后在CH3OH,CH3(CH2)3OH和HClO4组成的混合溶液中进行电解双喷,制备透射电镜(TEM)试样,利用Tecnai G2 20S型透射电镜观察各试样的衍射斑点以及明/暗场像。
2 实验结果
2.1 拉伸力学性能
图1为Ti-15Mo合金在298 K和573 K下经不同应变速率拉伸后的拉伸曲线。基于此得到了屈服强度(YS)、抗拉强度(TS)、均匀伸长率(uEL)、总伸长率(tEL)和断面收缩率(RA),如表1所示。同一应变速率下,合金的屈服强度在上述变形温度下变化不大,抗拉强度在573 K下相较于298 K下均明显减小,均匀伸长率、总伸长率以及断面收缩率均随变形温度的升高而减小(图1(a-1),(a-2))。在298 K下,随应变速率由5.21×10-4s-1增加到5.21×10-1s-1,屈服强度由438 MPa增加到458 MPa;而抗拉强度由703 MPa减小到660 MPa;均匀伸长率、总伸长率、断面收缩率和加工硬化率(work hardening rate, WHR)均逐渐减小(图1(a-1),(b-1))。而573 K下,随应变速率的增加,屈服强度由430 MPa增加到464 MPa;抗拉强度由587 MPa减小到570 MPa;均匀伸长率、总伸长率、断面收缩率和加工硬化率较室温减小幅度更小(图1(a-2),(b-2))。由此可见相较于298 K,应变速率在573 K下对Ti-15Mo合金的屈服强度具有更大的作用,然而对其应变硬化行为影响较小。
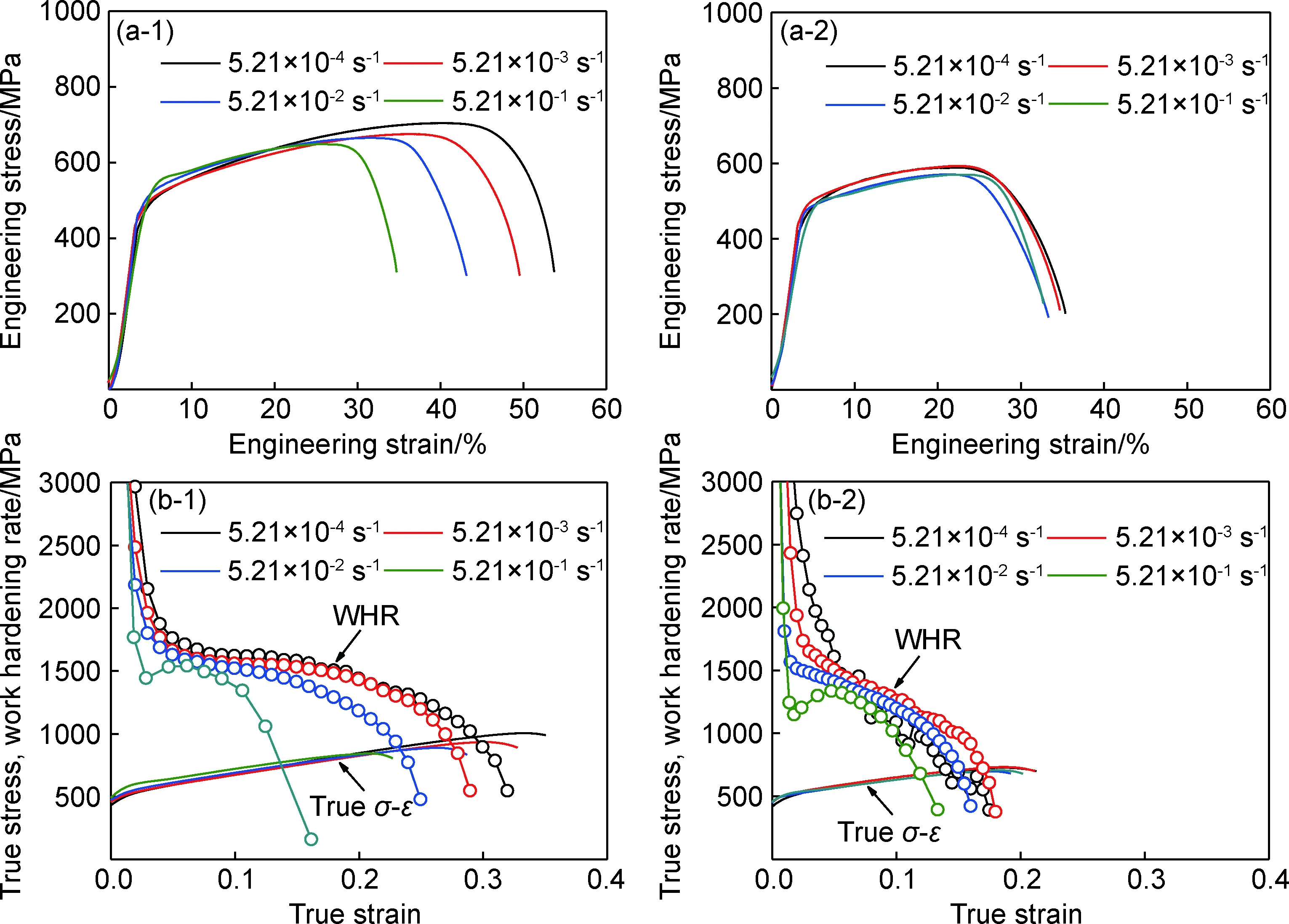
图1 Ti-15Mo合金在298 K(1)和573 K(2)不同应变速率下的拉伸曲线

表1 298 K和573 K下Ti-15Mo合金在不同应变速率下的YS,TS,uEL,tEL和RA
2.2 变形组织观察
图2为Ti-15Mo合金在573 K下于5.21×10-4s-1和5.21×10-1s-1应变速率拉伸后纵截面变形组织的OM图。不同应变速率下均有大量板条状组织产生,并且近断口区域晶粒被明显拉长。此外,板条状组织数量随远离断口逐渐减少。相较于低应变速率,高应变速率下有更多的板条状组织产生。对该合金在298 K和573 K下经不同应变速率拉伸后,距离断口8 mm处的变形组织做进一步观察,如图3所示。298 K下,不同应变速率变形后均观察到大量的板条状组织,交割成网状(图3(a-1)~(d-1))。低应变速率下,其交割明显,表明产生严重的塑性变形(图3(a-1),(b-1));随应变速率的增加,交割程度逐渐减弱(图3(c-1),(d-1))。相较于298 K,573 K下变形后板条状组织数量明显减少(图3(a-2)~(d-2));随应变速率的增加,板条状组织的数量却有一定程度增加。

图2 Ti-15Mo合金在573 K下于5.21×10-4 s-1(a)和5.21×10-1 s-1(b)应变速率拉伸后纵截面变形组织OM图

图3 Ti-15Mo合金在298 K(1)和573 K(2)下于不同应变速率拉伸变形后变形组织OM图


图4 Ti-15Mo合金在573 K下于5.21×10-4 s-1应变速率拉伸后变形组织EBSD图
图5为Ti-15Mo合金在298 K和573 K下于不同应变速率拉伸后的变形组织。基于修正的瓦伦-艾弗巴赫法得到的位错密度如图5(a)所示。在298 K和573 K下,位错密度随应变速率的增加分别由13×1014m-2和4.8×1014m-2减小到8.8×1014m-2和3.5×1014m-2。统计得到的{332}〈113〉孪晶的面积分数如图5(b)所示。在298 K下,孪晶面积分数随应变速率的增加由71%减小到55%;而在573 K下,其由30%增加到33%。由此可见,298 K下应变速率的增加会显著抑制Ti-15Mo合金中变形组织,即{332}〈113〉孪晶和位错的产生,然而变形温度(573 K)和应变速率耦合作用对变形组织的影响较小。

图5 Ti-15Mo合金在298 K和573 K下于不同应变速率拉伸后的变形组织 (a)位错密度;(b){332}〈113〉孪晶面积分数
3 分析讨论
3.1 变形温度和应变速率耦合作用对屈服强度的影响
传统金属材料的屈服强度随变形温度的降低与应变速率的增加而逐渐增大,并且BCC结构金属的屈服强度对变形温度和应变速率更为敏感[20-21]。然而,具有TWIP效应的Ti-15Mo合金的屈服强度在298 K下和573 K下表现出相似的屈服强度。图6为Ti-15Mo合金的TEM图。如图6(b-1),(b-2)所示,合金在573 K时效10 min后相较于ST试样,ω相明显增多,表明产生了等温ω相。这些贫Mo等温ω相的析出使其变形方式由{332}〈113〉孪生和位错滑移共同组成[14],位错滑移更高的临界分切应力(critical resolution shear stress, CRSS)补偿了温度升高导致的屈服强度的下降,从而使其表现出不同于一般BCC结构金属屈服强度的温度依赖性。此外,前期研究表明[14],在573 K下时效10 min内,Ti-15Mo合金的硬度快速增加,而随着时间的进一步延长,其基本不变,表明时效ω相的数量在10 min内显著增加。将拉伸试样置于炉子中到重新升高至测试温度的8 min导致ω相快速析出。此外,计算得到的绝热效应引起的温度升高值在5.21×10-1s-1下也仅为50 K,对ω相的析出行为影响微弱。因此,认为高/低应变速率下拉伸ω相的数量和尺寸基本相同。图7(a)为相较于5.21×10-4s-1下,Ti-15Mo合金在更高应变速率下变形屈服强度的增加值。随应变速率的增加(5.21×10-3,5.21×10-2,5.21×10-1s-1),298 K下屈服强度的增加值分别为4,12,20 MPa;而在573 K下,其增加值分别为14,19,26 MPa。由此可见,相较于298 K,应变速率在573 K下对屈服强度的影响更高,这与屈服过程中位错热激活行为密切相关。

图6 Ti-15Mo合金的TEM图
依据位错热激活理论,金属材料的屈服强度由σ0和σs两部分组成,其中σ0代表由固溶强化、细晶强化和弥散强化等组成的非热激活部分的贡献,而σs则代表依赖于变形温度和应变速率的热激活部分的贡献,本工作可用应变速率强化值表示。静态拉伸时,由于位错可以完全在热激活作用下克服局部障碍,可认为与变形温度和应变速率无关,所以σs忽略不计。本工作假设将298 K下、应变速率为5.21×10-4s-1拉伸得到的屈服强度作为σ0,σs则显著依赖于变形温度和应变速率,如式(1)所示[21]。
(1)
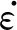
(2)
ΔV=MkBT/m
(3)
其中屈服点处的m可由式(4)求得:
(4)
式中σys为各应变速率下的屈服强度。
依据298 K于不同应变速率下的屈服强度,计算得到m为2.9 MPa,ΔV为260b3(b=2.54×10-10m,为位错柏氏矢量),其小于一般BCC结构金属的ΔV(10b3~100b3)。依据式(1),计算得到298 K和573 K下合金在各应变速率拉伸时的σs,从而计算得到理论屈服强度,如图7(b)所示。在298 K下,5.21×10-4,5.21×10-3,5.21×10-2,5.21×10-1s-1应变速率下的理论屈服强度分别为438,444,451 MPa和458 MPa;而在573K下,理论屈服强度分别为430,443,455 MPa和470 MPa,上述理论值与实验值基本一致。由式(1)可知,位错热振动频率随变形温度的升高而增大,即依靠位错热激活运动越过局部障碍物的能力增强,则573 K下位错热激活作用对屈服强度的影响更为显著。因此,随应变速率的增大,573 K下屈服强度的增加值高于298 K。综上所述,Ti-15Mo合金的屈服强度在298 K和573 K下依赖于位错的热激活过程,而573 K下更加显著的位错热激活作用使得屈服强度表现出更大的应变速率依赖性。

图7 相对于5.21×10-4 s-1, Ti-15Mo合金在298 K和573 K下更高应变速率变形屈服强度的增加值(a),实验和理论屈服强度(b)
3.2 变形温度和应变速率耦合作用对应变硬化行为的影响
随应变的增加,Ti-15Mo合金在变形温度(573 K)和应变速率耦合作用下呈现出较低的应变速率敏感性。在573 K下高应变速率拉伸后有更多的{332}〈113〉孪晶形成,这与298 K下明显不同(图3)。因此变形组织演变决定了不同的力学行为响应。
位错一般产生于具有较大应力集中的位错缠结以及晶界/孪晶界处,同时其演变过程依赖于位错回复过程。塑性变形过程中位错密度(ρd)见式(5)[19,22]。
(5)
式中:ε为塑性应变;ft为孪晶面积分数;k为位错存储系数;d为原始晶粒尺寸(102 μm);n和n0分别为塞积在晶界/孪晶界处的实际和最大位错数;fDRC为位错回复因子。n的演变可用式(6)表示[19,23]。
(6)
式中:εd为位错滑移产生的塑性应变;λ为滑移线间的平均间距(150 nm)[19]。由于{332}〈113〉孪晶的形成机制尚不清楚,无确切的模型来描述塑性变形过程中孪晶面积分数的演变,本研究借助马氏体形核模型[23],并依据{332}〈113〉孪晶具有的较小的CRSS来对其进行修正[24],如式(7)所示。
ft=fm{1-cexp[-β(ε-ε0)]}m
(7)
式中:fm为最大孪晶面积分数;c为优化因子;β为孪生动力学参数;ε0为产生孪晶的临界应变;m为常数(1.1)。进而可以得到位错平均自由行程(Λ),如式(8)所示。
(8)
式中t为孪晶厚度。
此外,对式(7)进行微分可以得到孪生速率,如式(9)所示。
{1-exp[-β(ε-ε0)]}(m-1)
(9)
图8为Ti-15Mo合金在573 K下,于5.21×10-4s-1和5.21×10-1s-1拉伸时理论变形组织的演变。塑性变形早期,高应变速率下需要产生更多位错来协调塑性变形(图8(a)),因此相较于低应变速率(k=0.030)表现出更高的k值(0.032)。高应变速率下产生的更多位错诱发更大的局部应力集中,从而促进{332}〈113〉孪晶的形成。此外,在573 K下应变速率增加导致的屈服强度增加值高于298 K(图7(a)),这更容易达到{332}〈113〉孪生的CRSS,从而进一步促进孪晶的形成。相较于低应变速率(β=8,c=0.80),高应变速率下具有更大的β值(12)和更小的c值(0.70),从而使其具有更高的{332}〈113〉孪生速率(图8(b))和更大的孪晶面积分数(图8(c))。塑性变形早期产生的更多孪晶会抑制后续孪生的形成,从而导致更小的孪生速率。此外,相较于低应变速率下fDRC=5.10,高应变速率下绝热效应引起的温度升高会引起fDRC增大到6.70,使得位错密度显著降低、应力集中减小,从而进一步降低孪生速率。低应变速率下更大的孪生速率使得高/低应变速率下的ft不断接近,但是塑性变形早期,高应变速率产生的更多孪晶依然使得该条件下具有更大的孪晶面积分数(图8(c))。低应变速率下更多位错的产生以及孪晶面积分数差值的减小使得位错平均自由行程的差值也逐渐缩小(图8(d))。
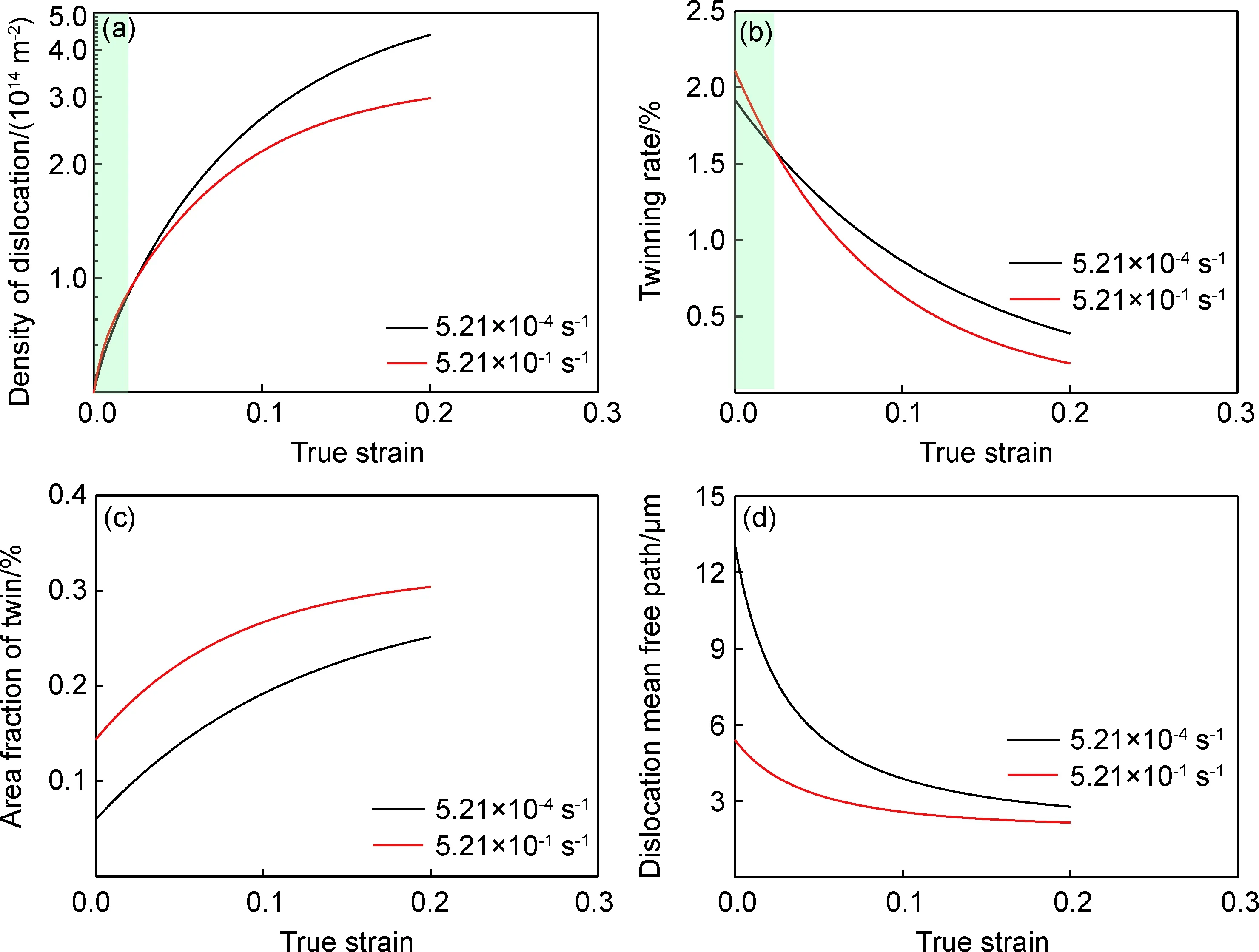
图8 Ti-15Mo合金在573 K下不同应变速率的拉伸变形组织
基于变形组织演变,可以进一步得到流变应力的演变情况。对于具有TWIP效应的β型钛合金来说,其流变应力由σ0、应变速率强化(σs)、位错强化(σd)和孪晶界引起的背应力强化(σt)四部分组成,如式(10)所示。
σ=σ0+σs+σd+σt
(10)
σ0由晶格阻力、固溶原子引起的固溶强化,晶粒细化以及ω相引起的弥散强化组成,如式(11)所示[25]。
(11)
式中:τCRSS为纯Ti的晶格阻力;Xi为原子分数;Bi为固溶原子硬化指数;ky为Hall-Petch系数(1112 MPa·μm1/2);γ为反相畴界能(0.15 J/m2);G为剪切模量(27 GPa);r和f分别为椭球状ω相的短轴长度(10 mm)和体积分数(0.7%)。基于理论变形组织演变,σd和σt分别可以由式(12),(13)计算得到。
(12)
(13)
式中α′为泰勒常数(0.36)。
图9为Ti-15Mo合金在573 K、5.21×10-4s-1和5.21×10-1s-1下σ的实验值和理论值,以及σd和σt对σ的贡献。高/低应变速率下,理论屈服强度分别为440 MPa和460 MPa,与实验值相似。其中,低应变速率下,σd和σt对其贡献分别为90 MPa和4 MPa (图9(a));而高应变速率下,σd和σt的贡献分别为96 MPa和18 MPa (图9(b))。随应变的增加,σd和σt对流变应力的贡献均单调增加,但是前者的贡献均高于后者。573 K下,{332}〈113〉孪晶的产生量明显低于298 K,导致孪晶界对位错阻碍作用较小,从而诱发较小的σt。高应变速率下,绝热效应引起的位错密度降低使得σd的增加率小于低应变速率。此外,高应变速率下塑性变形早期产生的更多孪晶对后续孪生的抑制作用使得σt的增速减慢。然而,上述更多孪晶的形成会进一步降低位错滑移不均匀分布引起的局部应力集中,使其依然具有更高的σt,并延缓颈缩的出现。综上所述,Ti-15Mo合金在573 K下,位错强化成为其主要强化方式,高应变速率下产生的较多{332}〈113〉孪晶有效降低位错不均匀分布导致的局部应力集中,从而延缓颈缩的出现,表现出更小的应变速率敏感性。
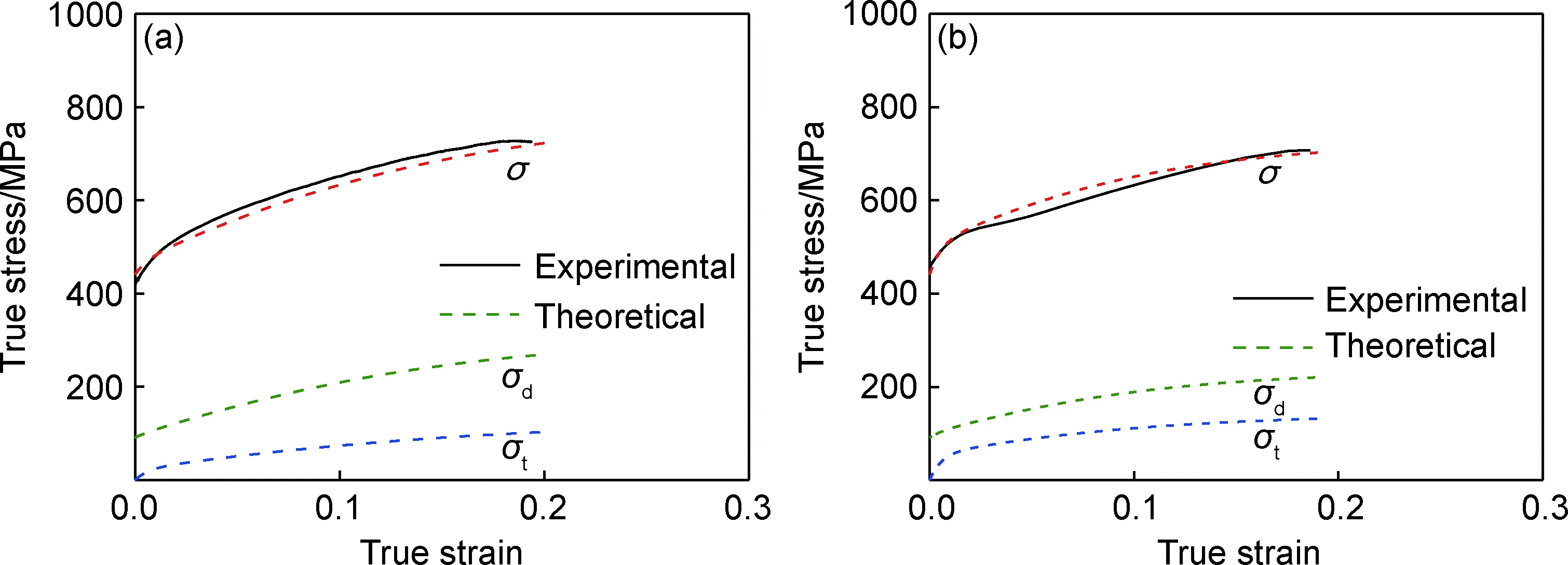
图9 Ti-15Mo合金在573 K下不同应变速率拉伸的流变应力模拟 (a)5.21×10-4 s-1;(b)5.21×10-1 s-1
4 结论
(1)Ti-15Mo合金的屈服强度在298 K和573 K下均随应变速率的增加逐渐升高;而相较于298 K下,应变速率在573 K下对其抗拉强度、均匀伸长率及加工硬化率影响较小。
(2)在298 K和573 K下,Ti-15Mo合金的屈服强度均依赖于位错热激活过程。573 K下,更加显著的位错热激活作用使得屈服强度表现出更大的应变速率依赖性。
(3)与298 K下不同,Ti-15Mo合金在573 K下通过{332}〈113〉孪生和位错滑移耦合变形,且位错强化为其主要强化方式。高应变速率下,塑性变形早期产生的更多孪晶虽然会抑制孪晶的进一步产生、降低加工硬化率,但同时其可以有效地降低位错不均匀分布导致的局部应力集中,延缓颈缩的发生,从而使得在573 K下随应变的增加呈现出更小的应变速率敏感性。
