基于Logistic 映射与矩阵像素置乱加密算法研究

杨永波，李 栋

（内蒙古工业大学 信息工程学院，内蒙古 呼和浩特 010051）

0 引 言

目前，通信技术处于快速的更新变换阶段，信息的传递变得更加便捷，但信息的运输和储存等安全性引起了人们越来越多的关注，保护信息的安全和防止非法盗取变得尤为重要，而使用加密算法是保障信息进行安全传输的有效方法之一。由于信息的数据量加大，其相关性也在增强，传统的信息加密模式已经不能满足当前信息加密的需要，而对混沌映射的研究为信息加密提供了新的方法。混沌映射的各态历经性、行为不可预测性、对初值和参数的极度敏感性等特性与信息加密的基本要求相符合。因此，研究混沌映射对于信息加密将有重要的意义。

混沌系统的特性非常符合图像加密的特点，使得混沌系统在图像加密方面的研究在现代密码学的研究领域中成为了热点。目前，数字图像加密的混沌模型有很多，本文提出一种新的对于图像信息的加密方案，利用传统的加密方法和混沌系统相结合，产生更复杂的加密方案。先对图像的像素进行置乱，让其形成随机序列；再对Logistic 迭代产生的随机序列用合适的方法生成密匙信息与明文信息做异或运算，形成密文信息序列。该方法大幅度降低了破译率，提高了信息的安全性。

1 混沌理论的概念

混沌具有复杂的运动规律，是一种不可预测的无序性行为，它内部结构丰富，而且也没有明晰的对称和周期，属于非线性系统。混沌理论是一种采用定量分析和定性思维的方法，被用来研究关于动态系统的行为。动态系统的行为只能用一个连续和完整的数据关系来解释和预测，而不能采用仅仅是单一的、片段的数据关系来解释。混沌系统的重要特征如下：对初始值及系统中各种参数的强烈敏感性，它自身所拥有的伪随机性、周期点稠密性、行为不可预测和拓扑传递的特征。其中的特征与密码学所要求的混合、扩散和随机性等特性相符。混沌系统的信号自身所具有的连续宽带频谱的特点、非周期的特征和它拥有的类似于噪声的特征，使其具有了自然而又隐蔽的特征。由于这些特性，混沌系统就会发展成为一个拥有优异的密码性能的系统。

2 基于矩阵像素置乱的加密

基于矩阵的像素置乱变换的基本原理是打乱像素原先的排列顺序，比如将一个像素的位置变换移动到另一个像素的位置，以此类推，使所有的像素位置发生变化，并使其从视觉上变成与原始图像毫无关系的图像。而本文对像素的值不进行任何操作。

置乱就是打乱像素的排列顺序，打乱排列的方法有很多种，比如幻方变换和Arnold 变换。单纯地打乱行排序或列排序，如图1 所示，很容易从密文推算出加密算法是打乱行排序，无法保障加密的安全性。

图1 行加密后图像

为了加大保密的安全性，通常在进行行列排序的同时，在加密算法中加入一个随机序列作为密匙结果，如图2 所示。

通过图2 可以看出：像素置乱的加密方法不会改变密文数据量，计算复杂度很小；但是安全性较低，即使通过较高复杂程度的随机变换矩阵，其加密的安全性依然较低，攻击者通过已知明文的攻击方法就能够轻易地获得加密时所使用的变换矩阵。以上这类加密算法的方式已经被时代所淘汰，目前的方式是使其和其他高级加密算法相结合，从而达到现代信息加密的要求。

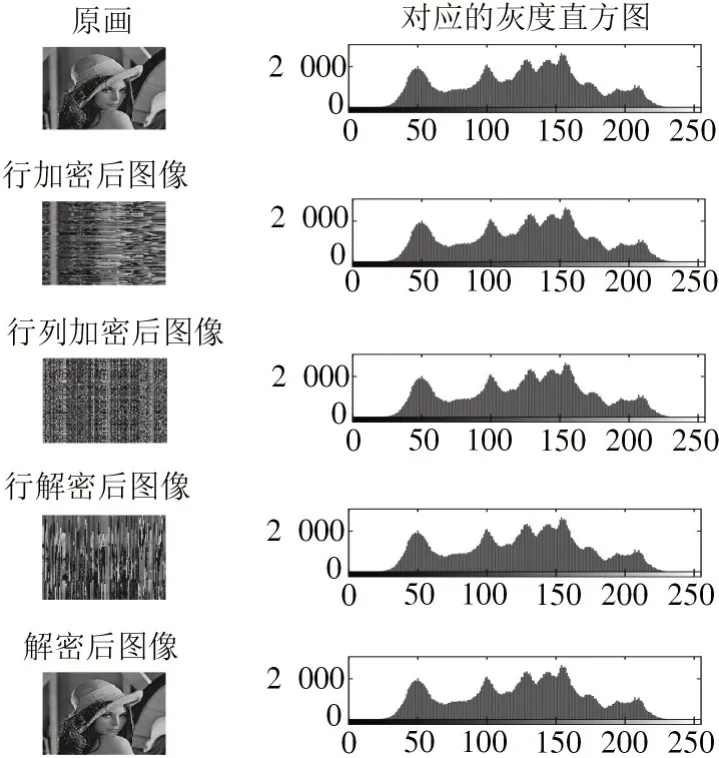
图2 基于矩阵像素置乱的加密结果

3 Logistic 混沌映射

Logistic 映射是一种简单的混沌系统映射，但其对初始值等初始条件具有敏感特性，还有着它本身的遍历性的特征，以及复杂的不可预测行为，使它在信息加密领域具有很广泛的应用。同时，Logistic 混沌映射也是被用于对动力系统和混沌等复杂系统方面的研究，其数学的表达式如下：

式中，当和满足相关的约束时，Logistic 映射函数就会转换成混沌状态。在模型的基础上，给定初值和，利用公式迭代次之后，就可以得到，，…，X这个值，这些值就构成了一个混沌序列。研究结果表明：当的数据值的范围为3.569 945 6<≤4 时，尤其当的值与4 无限相邻时，迭代后的值就可能会一直表现出伪随机性，即Logistic 映射出现混沌的情况。混沌现象对于初始值等条件是相当敏感的，行为也是完全不可预测的，现在被广泛应用在关于图像加密的算法中。当=4 时，具有下列典型的混沌特征：

1）不可预测性。当=4 时，Logistic 混沌映射在进行有限的迭代后，混沌值会在混沌空间中呈现出随机的无序运动。

2）规律性。X具有不可预测性的特征，但它是通过具有确定性的式（1）推断出的，初值确定后就能够获取X，即其不可预测特征是内在的，这就是混沌进行运动时所表现出的规律性。

3）对初始值的敏感性。混沌运动对初始值的敏感性是指初始值的微小变化都会使序列{X}有着巨大的改变。

4）遍历性。遍历性指的是变量在混沌空间中按其自身规律，使对所有的状态都能够来遍历。

Logistic 映射在进行算法迭代的运算后，混沌点将无规律地落在线段（0，1）上，下面是其概率密度的表达式，式（2）也被称为Chebyshev 分布。

图3 为Logistic 映射的分岔图，横纵轴分别命名为参数、迭代的状态值，分岔图反映的是动力系统的最终状态和控制参数的关系，以及概括系统的总体特性。

图3 Logistic 映射的分岔图

4 基于Logistic 映射的混沌加密

Logistic 映射有着其确定的形式，其中不包含任何随机成分，但迭代后的结果却像是处于完全随机的，即行为是不可预测的，而且对于参数和初值的变化极为敏感。由于以上特点，基于Logistic 映射的混沌加密算法对信息是安全的和无损的。对其采用对称加密算法，也就是说加解密的密匙是相同的。其加密和解密的表达式分别为：

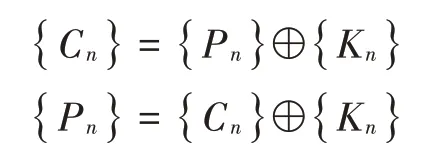
式中：{C}为密文信息序列；{K}为密匙信息序列；{P}为明文信息序列。

Logistic 映射的混沌加密是从迭代后的混沌序列中以一定的方法构成密匙信息，取一块待加密的明文，让该明文信息序列和迭代后的密匙信息一起做异或运算后获取密文序列。混沌序列加密、解密设计流程如图4所示，下面是对流程的简单描述：

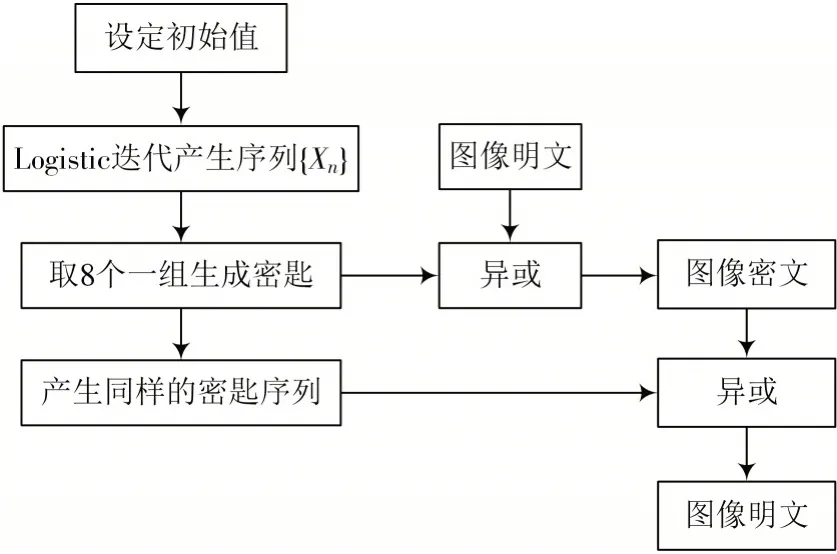
图4 混沌序列加密、解密设计流程

1）选取恰当的初始条件，将其代入Logistic 映射方程，迭代后形成随机序列；

2）将该随机序列以一定的方法形成密匙信息序列，与要加密的明文信息序列进行异或运算，得到密文信息序列，并由发送端传到接收端；

3）选择相同的密匙信息序列，让其与接收到的密文信息序列一起来做异或运算，将得到原始信息序列。

5 基于Logistic 映射新的加密解密算法的具体实现

在基于混沌映射的加密方法的实现中，着重点是混沌信号的序列流程的实现，本文方法如下所示：先设定一个迭代的初始值和控制参数；然后通过Logistic映射公式迭代生成序列{X}，取8 个一组生成密匙；再与图像明文信息做异或运算得到图像的密文信息；最后产生同样的密匙序列，与图像密文信息做异或运算得到图像的原始信息。当初始值相近时，为了使它们的混沌序列是无关的，在仿真过程中迭代1 000 多次才进行取值，能够有效地放大误差，使对初始值等条件的攻击无效，则信息加密的效果更好。由于本文加密的信息是数字量的，要使这些实数组成的混沌序列{X}进行映射，使它们都转换成由整数组成的伪随机序列，进而来作为加解密的密匙。在进行迭代1 000 多次后，开始对序列进行处理，8 个为一组，由它们作为密匙，若它们大于0.4，则数字化为1；若小于0.4，则数字化为0。取=0.720，=3.998 作为密匙，用Matlab 仿真，其仿真结果如图5 所示。

由图5 可以看出，加密后图像的像素发生了变化。由于混沌加密算法的随机性较强，其密匙的保存与传输相比较于其他加密算法，特别是传统的矩阵像素变换加密算法方便了很多。下面是使用混沌加密算法的典型优点：

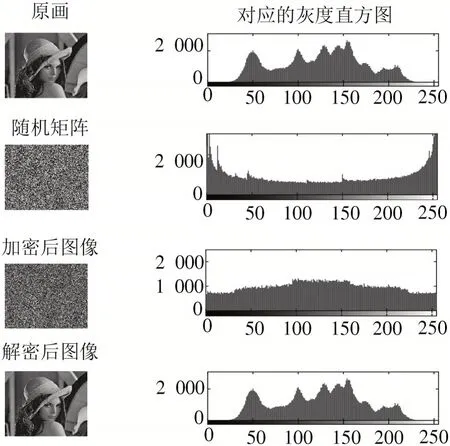
图5 Logistic 映射新的加解密

1）提高了安全性。混沌加密算法对控制参数和初始值等条件的选择有着非常高的敏感性，此外，通过混沌系统的运行产生了庞大的密匙集。由于混沌具有遍历的特征，所以可以将密匙均匀地分布在整个密匙集中。因此，混沌加密算法大大地提高了安全性。

2）代价小。代价指的是运行算法时所需的时间代价和算法储存时必需的空间代价，时间代价指预先准备和进行加密过程所需的时间。预先准备时间是在加密之前用一定的方法来获取密匙序列，加密过程所需的时间指的是密匙序列对明文序列信息进行运算处理。混沌加密是流密码所在领域里的知识的运用，其所花费的预先准备时间很少；加密时只是对明文序列信息进行异或运算，其所需的时间大部分是消耗在密匙流的产生过程中，相比其他的加密算法，比如说现在更受欢迎的分组加密算法，其消耗的时间是很少的。空间代价包括使用该算法所需的静态空间以及对于使用该算法时所必需的运行态空间。静态空间为执行所必须的运行编写代码的长度消耗的空间，运行态空间为在进行加密操作的算法中所占据的临时性空间。该算法通常所用的临时变量非常少，此外，它在进行循环后获取密匙流时只寄存少许的变量，所以在系统运行时只使用少量的空间。

3）易于实现。运用混沌加密算法能够进行信息的加密、信息的解密和充当随机数发生器，其加密和解密的算法工作过程是能够进行重用的，相比其他加解密算法而言，可以更容易实现。

6 实验结果与鲁棒性分析

6.1 直方图分析

图6 和图7 分别是新算法的原始图像和产生加密后的图像的灰度直方图。通过对比，从加密图像的灰度直方图中可看出其灰度值呈均匀的分布，这有效地遮盖了原始图像中像素的分布特征，未见任何原始图像的信息，使攻击者不能通过灰度直方图分析时获取到原来图像的信息。由此可以得出，此种方式的加密技术能够有效地防御统计学分析的攻击和已知密文的攻击。

图6 原始图像及其直方图

图7 加密图像及其直方图

6.2 信息熵的分析

从信息概念和理论识别角度来看，信息熵主要可以广泛地应用在对于混沌程度的整体性度量和对于混沌程度的识别。如果一个混沌体系的各种动态和行为都表现得越有序，那么它们的信息熵就会变得越低；相反，如果混沌体系的各种动态和行为是杂乱的，灰度的分布也就越是均衡，其中信息熵就是要找的理想值。其表达如下：

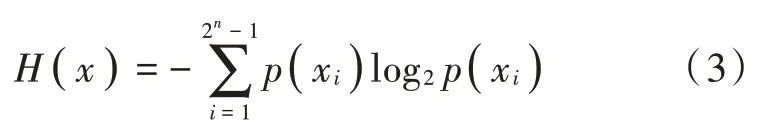
当信息熵非常接近8 时，说明算法对图像的置乱充分，不确定性高，加密算法能有效地防御对于信息熵的攻击。

6.3 初始值敏感性验证

混沌的初始值敏感性指的是当初始条件出现细微的变化时，迭代一定次数后系统的状态会发生很大的变化，甚至会变得完全不相同。如图8 所示，2 次实验初始值为：=0.400 0（黑色）和=0.400 1（灰色）。

由图8 可以看出，当初始值改变很细微，进行很少的迭代次数时，结果是基本相吻合的；但是当迭代达到一定次数时，结果会出现明显的差异。这就是混沌对初始值的敏感性。

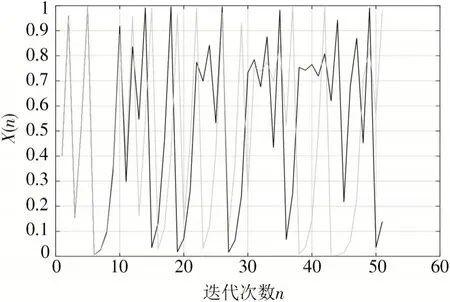
图8 初始值敏感性验证

6.4 密匙敏感性分析

图9 所示在其他密匙均不发生变化的情况下，各自选取初值误差10，参数误差10时的解密图像。在密匙误差变化极其细微的情况下，密文图像也无法还原成原始图像。图10 为输入精准的密匙时输出的结果。由图10 可得，算法对密匙比其他加密的方法有着更高的敏感性。Matlab 数据为双精度浮点的实数，该算法对初始值和参数的密匙空间的数量级能达到：10×10×10×10=10≈2，相 当 于 一 个 长 度 为192 位的二进制数，可见密匙空间是足够大的，能够防御各种攻击。

图9 错误解密图像

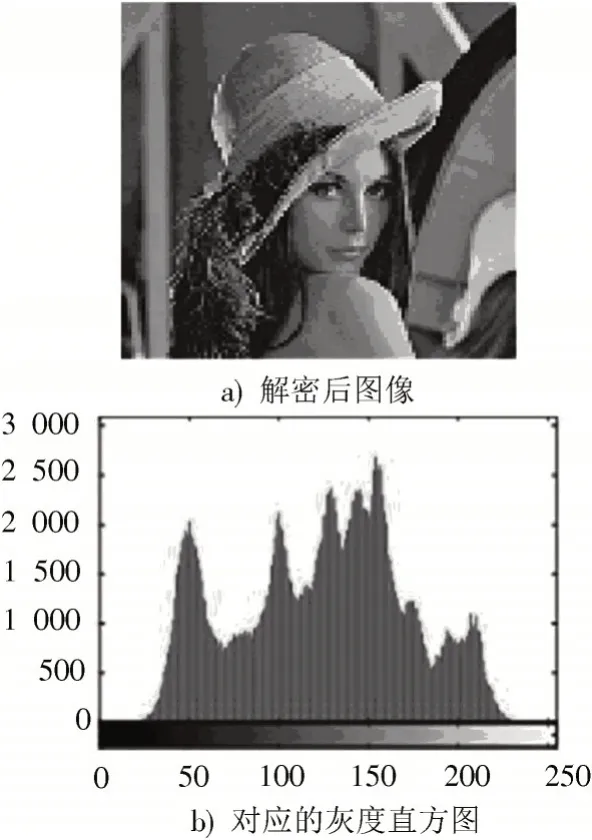
图10 正确解密图像及其直方图

6.5 抗干扰能力分析

图像在传输过程中经常会遭受到各种不同的干扰，加密图像应对这些情况具备较强的防御性。图11a）是对于剪切部分的密文信息后的图像，图11b）是在完成图11a）的操作后再次进行密文解密后的图像，图11c）是对密文信号进行高斯噪声干扰后再次解密输出的图像。从实验结果中可以清楚地得出，该算法具有较强的抗干扰特性。

图11 密文图像受干扰解密

7 结 语

从Logistic 映射的混沌加解密算法的分析中可以得出，混沌加密算法有很多优点，最主要的优点是提高了安全性，能够轻松地对算法进行实现，并且实现的代价是非常小。传统方法基于矩阵的像素置乱变换加密，不会改变密文序列的数据量，只对图像的像素排列顺序进行打乱，因此计算的复杂度很小，但也导致安全性较低；并且像素置乱不会改变像素值，灰度图像不会改变，但提出的新的加密算法正好克服了这一问题。

由于进行Logistic 混沌加密时先对像素做了置乱处理，故Logistic 混沌映射像素值位置不变的缺点也被像素置乱弥补。选用先对图像进行像素置乱再进行Logistic 混沌映射的加密，系统的安全性会更高。此外，通过鲁棒性分析，加密图像灰度分布均衡，能够有效地防御统计学分析的攻击和已知密文的攻击，对密匙有着极高的敏感性，还能抵抗多种攻击，具有极好的安全性，能满足安全传递信息的要求。

为了提高系统加密的安全性，如果进行多混沌系统加密将能够大幅度提高信息传递的安全性，因此，下一步需要研究的是尽量将多个混沌系统相混合，以免造成混沌系统的信息直接暴露出来，或者是研究更高级的混沌系统去寻找出抗攻击性更强、保密性更强的混沌加密方案。