面向环境监测的传感器网络边缘检测研究

刘世泽，范书瑞，郭书纬，贾颖淼

（1.北京航空航天大学 软件学院，北京 100191；2.河北工业大学 电子信息工程学院，天津 300401）

0 引 言

近年来，我国经济由高速增长阶段转向高质量发展阶段，改善环境日渐成为人们的迫切需求，空气质量检测已经成为全体人民关切的头等大事。本文结合传感网络的边缘检测技术，通过边缘检测算法以及一系列未知点的预估策略，直观得到区域空气污染物浓度分布状况；再根据污染的分布情况对症下药，以更加高效地治理环境污染等问题。

由于监测站点是离散随机分布的，现如今常用基于图论知识的Relative Neighborhood Graph（RNG）和Gabriel Graph（GG）拓扑连接规则组成一个传感网络结构。Shu Lei 等提出了一种基于RNG 和GG 的平面化边缘检测方法，该方法是一种高效的连续目标边界监测方法。传感器存储单元内含有与它相邻节点的检测状态，如果节点读取到的状态出现某种边界节点特征，就可以锁定边界节点，从而极大地节约无线传感网络能量。但是通过监测节点浓度和坐标进行边界节点检测只考虑有限的边界节点，对于实际复杂的环境是远不够的。因此，文献[2]进行了关于无线传感网络空洞检测方面的研究，考虑工厂环境下可能存在的污染气体泄漏问题，并针对最有可能和最有价值的传感网络空洞进行修补。为了能获得完整的传感器网络事件边缘，师泽源等人提出了一种基于扩展场强模型的稀疏AQI 空间插值新算法，这种方法利用最小均方根误差得出参数值，与同样基于空间分布的反距离插值法和权重质心法相比，在空间插值方面更加精准。

然而以上插值方法仅利用单一距离权重，没有考虑风速对空气中颗粒物的扩散作用。为了更加贴合实际，本文采用一种顾及风向和风速的空气污染物浓度插值方法。该方法强调结合风速和风向以及距离三种因素，继承了气体扩散模型中“扩散”的思想，针对区域进行插值预测，具有更加良好的效果。

1 经典传感网络拓扑结构

大部分的无线传感网络节点无法更换电池，所以无线传感网络是一个对功耗有极为严格要求的网络，需要使用能够有效延长传感器节点寿命的拓扑控制方法。常见的拓扑图有最小生成树（Minimum Spanning Tree，MST）、相 关 邻 近 图（Relative Neighborhood Graph，RNG）、泰森多边形（Voronoi Graph）等。

1.1 基于RNG 规则的边缘检测方法

邻近图是一种并不复杂的几何图形，由于其顶点满足某些特殊要求，可通过连接他们的顶点形成图形的边，使其具备一定的几何特性。在无线传感网络中，邻近图可以用来连接无线传感网络节点的拓扑结构。相关邻近图是为了使所有节点选出距离自己最近的节点作为自己的邻居进行连接。

相关邻近图连接方法如图1 所示。顶点，与其他顶点满足以下条件：，距离小于等于到的距离和到的距离的最大值，即在∀≠的条件下满足：

图1 RNG 平面示意图

1.2 基于泰森多边形的孔洞填充

唐山市开平区空气监测站点过少，需要采取类似的空洞填充策略，将未覆盖的区域进行插值填充。为了解决在无线传感网络中的边缘检测和传感网络空洞填充的问题，除了平面邻近图这样的通过传感器节点和通信链路组成的几何图形，还有德劳内（Delaunay）三角图、泰森多边形等基于点线几何平面关系建立的几何图形，它们都具有良好的空间分布特性。

泰森多边形解决的实际问题是利用离散的随机点将区域分割成不同区块，每个区块的中心点是某一个离散点，任何一个点到达所在区域的离散点的距离相较于其他离散点是最近的，一般可将该离散点的特征作为所在区域泰森多边形的特征。Delaunay 三角图和泰森多边形是在城市规划中依据城市相互作用理论对城市进行空间分割常用的方法。在环境监测领域，泰森多边形是对城市进行区域划分使用较多的方法，它可以突出多种因素影响下的城市分布特征。

2 基于距离的空间插值方法

利用RNG 的图论知识可以判断出边界节点，继而通过边界节点的连线判断出大致边界，但是存在节点分布稀疏、精确度不足的问题，因此本文利用泰森多边形对区域的潜在空洞位置进行填充。从泰森多边形上看，节点分布密集的中心城区有良好的填充作用，但对边界的作用并不明显。现在有很多种不同的插值方法可以选择，本节拟采用反距离权重算法和基于场强模型的空间插值算法两种不同的基于距离的空间插值方法，呈现更加精确的边界信息。

2.1 反距离权重算法

反距离权重算法是一种十分简单的插值方法，它主要依赖于反距离的幂值，幂参数可基于距输出点的距离来控制已知点对内插值的影响。该方法中，每个输入点对最后结果都有着局部影响，影响随着距离的增加而减弱，所有影响的叠加求和即为此点的待估值，其算法步骤如下：

1）计算出待测点到已知点的距离：

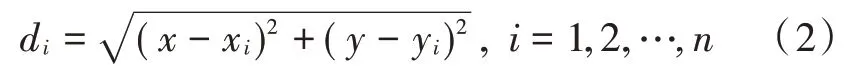
2）根据需要，取个距离待测点最近的已知点，权值为距离的倒数，表示为：

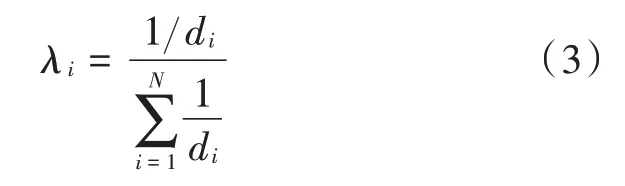
3）将各部分叠加起来作为估计值，即：

2.2 基于场强模型的空间插值算法

空间插值理论适用的前提是待插值的对象有着明显的空间分布特征，不同对象具有一定程度的空间分布相似性。因此，场强模型就是从物理学上的电荷电场分布进行类比后得出的一种计算空间插值的方法，相对于其他的依据地理位置信息的计算方法，在均方根误差方面更具有优势。本节采用了场强模型插值对空间区域进行插值预估，场强模型如下：

式中：q是一共个已知节点中的每一个节点的数值；r是，点的经纬距离，是受已知点的影响叠加出来的插值结果。

结合气体浓度符合空间特性的结论，利用扩展场强模型算法找到合适的值，并计算RMSE，计算流程为：

1）随机选取个已知节点的任意节点，与其余-1个节点计算距离，此时设置=1，代入式（5）计算插值E；

2）将得到的插值E与已知节点γ做差，得到ζ；

3）计算均方根误差RMSE，计算公式如下：

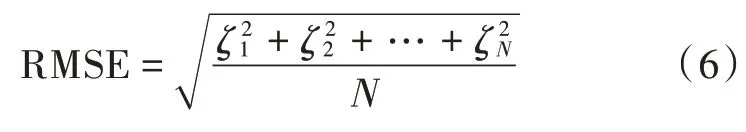
3 估计风向和风速的插值方法研究

传统的以距离为单位的插值方法在大气稳定的情况下，具有简单、效果良好的特点。但是在日常环境中，风对于气体扩散有着重要的影响，单纯的运用单一距离为权重的插值在精确度方面低于利用风速风向的扩散模型的插值方法。利用风速风向的扩散模型的插值方法流程如图2 所示，首先利用空间插值方法获得整个区域的风场数值；其次计算一种基于风场数据的相邻单元扩散距离；再结合经典的Dijkstra 最短路径算法，把相邻单元扩散距离结果转化成一种有向权邻接矩阵，矩阵内的参数为相邻两点之间的路程，利用最短路径算法，找出风场的最短路径；最后利用反距离权重法求解出待测点的污染气体浓度。

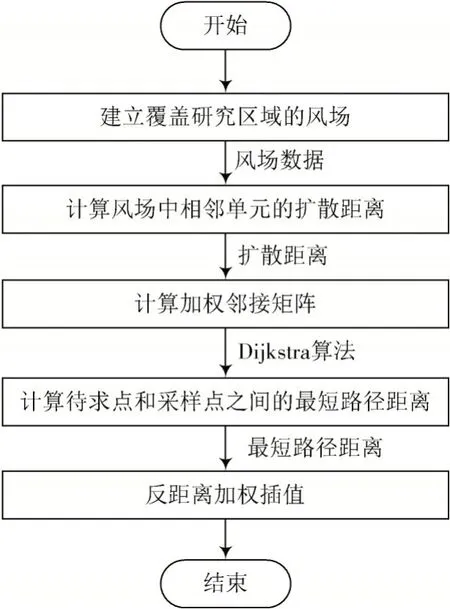
图2 风向和风速的空气污染物浓度插值方法

3.1 相邻单元扩散距离算法

计算基于风场数据的相邻单元扩散距离的目的是生成有向权邻接矩阵，矩阵内的数值就是相邻单元扩散距离，计算公式为：

式中：Cost 是相邻单元扩散距离，它是由函数、参数、参数共同构成；函数由风向作为影响因子；和分别代表a 和b 网格单元处风向所表示的方位角；D代表ab 方向的方位角。函数考虑风向因素对于相邻网格单元间扩散的影响，下风向的扩散距离小，上风向的扩散距离大。

式中：权重和充分顾及风速因素对于扩散的影响，对于下风向，风速越大扩散距离越小，对于上风向，风速越大扩散距离越大，指数上面的符号函数通过判断风向得到，如果是同一方向，则对权重的指数是正数，对结果影响较大，如果不是同一方向，则权重中的指数为负，整体权重就会偏小。用上述方法计算出有向加权邻接矩阵的元素，得到有向权邻接矩阵。

3.2 Dijkstra 最短路径算法

最短路径是指在每条边都有权重的连接图中，两个点之间的所有权重相加后最小的那一条路径。计算机在对路径进行遍历计算时，当出现更短路径时，会替换掉先前路径，保证路径的权值是最短的，缩短距离的过程称为松弛。经典的最短路径算法有Dijkstra 算法、Bellman⁃Ford算法等。Dijkstra 算法不需要对边进行迭代松弛，而是选择与初始点最近的起点开始，不断选择距离起点最近的顶点。Dijkstra 算法也有松弛行为，但并不是盲目地对任何一条边进行重复性松弛计算，它是根据已确认的最短路径点到下一个待确认点的路径进行松弛。因此选用该方法是为了在进行不同浓度贡献度叠加时，选择的是最有效果的扩散路径。

4 实验结果与分析

4.1 实验数据

本文使用的数据是唐山微型站2018 年2 月小时数据，里 面 涵 盖 的 是 从2018 年2 月1 日00：00 开 始 到2018 年2 月28 日23：00 为 止 详 细 的 污 染 物 浓 度 数 据。这些数据来自唐山市的路北区、开平区、丰润区、古冶区等9 块区域，400 个监测站。采集到的数据包含有PM，PM，SO，O，NO，CO 多种污染物数据的统计，考虑到数据库数据庞大，本次实验选择开平区2 月数据进行相关研究。

4.2 经典拓扑结构结果

4.2.1 RNG 方法实现

对目标区域节点依据地理位置信息，利用geopy 库中的geodesic 函数，将经纬距离转化为以千米为单位的实际距离。对整个传感网络分块划分，将区域内的全部节点分别作为当前计算的中心点，称之为点，而判断是否可以连通的计算点称为点。点的范围是除了点以外的点都要成为一次节点，点是作为判断，能否连通的关键条件，每一个点都要参与检查自身点是否存在于，的RNG 规则区域内。最终得到拓扑图如图3 所示。

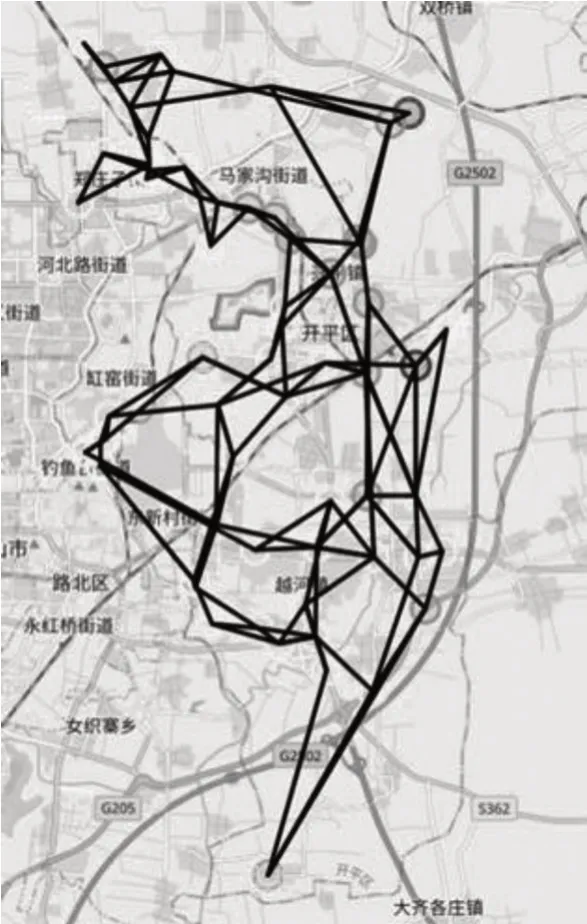
图3 开平区PNG 拓扑图

由图3 可以看出，两节点之间的连线较长，图中存在明显的空洞。在得到了整张区域图的节点信息后，将节点浓度指数（如PM）按照国际标准的颜色对应检测站点数值，在地图上呈现出来。图中绿色节点PM浓度小于35 μg/m；黄色节点PM浓度在35~75 μg/m之间；橙色已经是轻度污染，PM浓度在115~150 μg/m之间；红色是重度污染，浓度为150~250 μg/m；紫色为严重污染，浓度在250 μg/m及以上。

4.2.2 泰森多边形孔洞实现

本文利用泰森多边形数学上的特性进行空洞填充。由于预测空气检测站点分布稀疏，相应多边形区域面积较大，无法准确预估空洞地区的浓度情况，故利用泰森多边形的相关性质，其在无线传感网络的空洞填充方面上具有良好的特性。

泰森多边形最重要的性质为每一个泰森多边形内任意一个点到所在多边形的内部已知点距离是最短的，即如果出现了传感网络空洞，空洞最容易存在的位置是泰森多边形的顶点位置，该位置若未被传感器节点检测区域覆盖，且由于该点距离多边形中心点的距离是最大的，因此该位置出现空洞的可能性和空洞面积相比其他位置是较大的。图4 所示为开平区监测站构建的泰森多边形。图4 中，轴为纬度，轴为经度，蓝点是监测站点，红线交叉点是需要进行节点填充的位置。

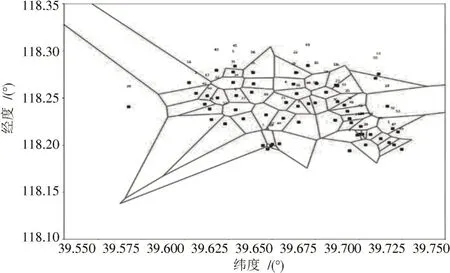
图4 开平区监测站泰森多边形

从图4 可看出，相较孔洞填充前，区域中心位置节点密度明显增强，但是对于处在地图区县边缘的节点，依然稀疏，无法精确地检测该区域的边界。传感网络空洞最容易存在的位置是泰森多边形的顶点位置，该位置若未被传感器节点检测区域覆盖且由于该点距离多边形中心点的距离是最大的，因此该位置出现空洞的可能性和空洞面积与其他位置相比是较大的。

4.3 基于距离空间插值结果

4.3.1 反距离权重法结果

应用反距离权重法对区域坐标进行插值，其结果如图5 所示。

以距离的倒数为权重的预测方式，从图5 上看，呈现的是一个向外的类似圆形区域，根据反距离权重法的原理，距离越远，浓度越小，但在精确度方面并不是很好。

图5 基于反距离权重法的插值结果

4.3.2 基于场强模型的空间插值结果

根据式（5）、式（6），计算不同条件下的值以及RMSE 数值大小。当值很小的时候，整个权重对于距离的依赖程度会很高，分母很小会造成场强叠加的数值变大，不同点的插值结果差异较大；而当值很大时，会造成整个分母所占比重较大，距离对最终叠加值的影响较小，并且分母数值过大，造成叠加值大小变得平滑且数值偏小。因此，将参数的数值以0.1 为间隔均匀增加，根据式（5）、式（6），计算不同条件下的值和RMSE 数值大小；RMSE 小，代表着当前值是在若干中误差最小、最具有代表性的，则选择此值完成场强的叠加并计算最终的插值。空间场强的插值方法最终结果如图6 所示。

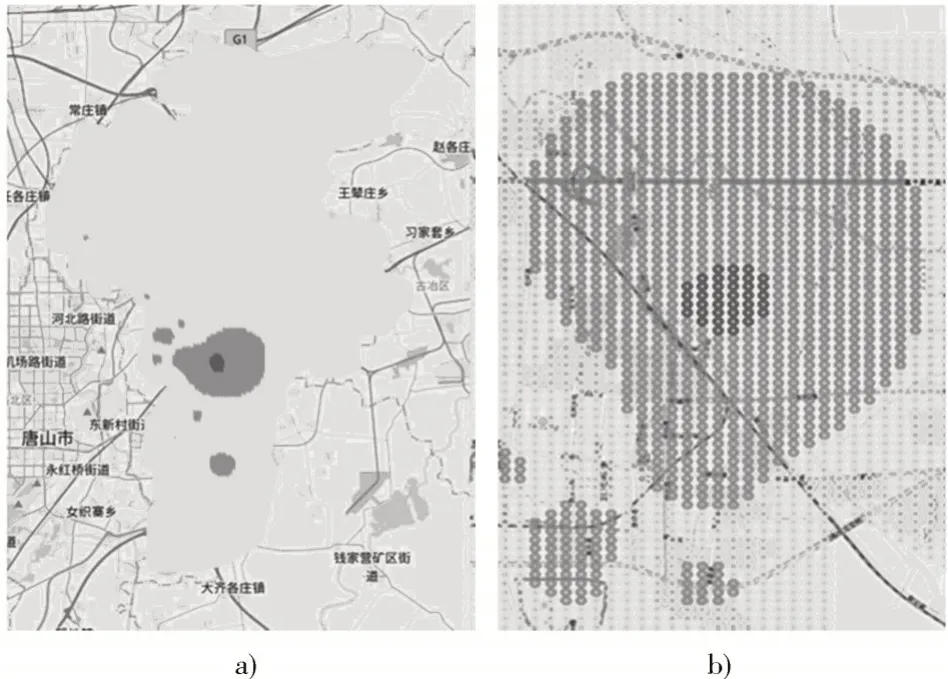
图6 基于扩展场强模型的插值结果

4.4 顾及风向和风速的插值结果

图7 为顾及风向和风速的空气污染物浓度插值结果，结合地理和气候环境情况分析如下：浓度最高的区域为开平站附近周围3 家大型耐火材料工厂和1 家冶金行业工厂。到了冬季，锅炉等需求量大，因此耐火材料需求量也相对旺盛。生产耐火材料所需的大部分原材料（以矿渣、玄武岩及白云石为主）都是经过焦炭为燃料煅烧或电熔后才能使用的，并且在生产过程中还伴有主要成分为粉尘和SO的冲天炉废气的产生。另外在上料过程中，由于传送皮带之间、皮带和送料口之间存在高度差，造成部分物料形成扬尘。开平区南部存在另一个严重污染区域，该区域地处开平工业区，工业污染较为严重。

图7 顾及风向和风速的空气污染物浓度插值结果

4.5 结果分析

2 月份正值中国新年之际，烟花爆竹的燃放会造成PM、PM、CO 升高，严重地影响空气质量，并且当气温较低，大气层对流运动较弱时，污染物易堆积在近地面，不利于污染物消散，会加剧污染造成空气质量变差。同时冬季的相对湿度小，降水净化能力弱，不利于空气质量的改善。将三种插值方法得到的PM浓度与真实浓度对比，得到的折线图如图8 所示。本实验选择的监控站是冀东水泥二分公司东南808727 站点。由图8 可知，三种方法与真实值的折线趋势大致相同；当PM数值较小时反距离权重法更接近真实值；当PM数值较大时，风向风速插值法更接近真实值。2 月前12 天，三种方法差距不大；后16 天PM浓度增加，三种方法结果出现较明显差距。

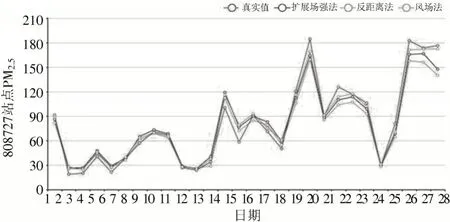
图8 三种方法对比折线图

为了直观地体现各种空间插值方法的实验结果误差，将三种插值方法的根均方误差（RMSE）计算出来，如表1 所示。由表1 可知，风向和风速插值法方法与扩展场强插值法的插值结果精度相近，反距离插值方法的插值结果精度明显低于扩展场强插值法和风向风速插值法，而本文重点研究的风向风速插值方法的插值精度相比扩展场强插值方法又有所提高。

表1 三种方法的根均方误差

5 结 论

使用传感网络对污染区域进行边界检测，相比人工手持设备检测浓度，不但可以提高检测效率与精度，监测范围也显著的扩大。但是固定的监测站点少、流动性差，分布不均使得无法直接对相关区域浓度进行全方位监测。本文基于唐山市各区县空气污染数据，对丰润区的几十个传感器节点进行边界划分，可以清楚地得到污染区域的传感器边界节点，通过对边界节点的连线可以初步确定边界的大致形状。由于传统的气体扩散模型过于复杂，并且参数很难确定，文中采取一种风向风速气体扩散模型，将空间点转换为一种元素为距离的有向权邻接矩阵，利用反距离权重法得出预测点浓度大小。最终结果比以上其他方法更为精确，均方根误差最小。