基于关联度分析组合法的电网负荷预测
2022-08-13国家电网西藏电力有限公司巴河发电公司
◇国家电网西藏电力有限公司巴河发电公司 何 川
针对电网内部发电机组的启停,电网运行的安全稳定,安排机组检修计划等问题,对电网负荷进行预测。本文基于灰色预测模型,BP神经网络模型,提出了一种关联度分析组合法的预测模型,并应用了实例。结果表明,本文所提出的新型预测模型比任一单项模型预测值更加精确,实用性较强,值得推广应用。
电网负荷的预测有利于决定未来新的发电机组的安装,决定装机容量的大小、地点和时间,决定电网的增容和改建,对电网的发展具有重要意义[1-2]。电力负荷预测方法可分为基于统计方法和基于机器学习方法两大类。在基于统计方法中,常用方法有自回归模型、卡尔曼滤波法等;在基于机器学习方法中,可分为传统机器学习方法和神经网络方法。其中,传统机器学习方法有支持向量回归(support vector regression,SVR)[3-4]、决策树及其集成算法,如随机森林[5]、梯度提升回归等。基于此,本文应用灰色预测法GM(1,n)与BP神经网络法的预测结果建立最优预测模型,并对电网负荷进行预测,希望为电网优化运行,电力系统规划提供参考,并以某地区实际电网负荷数据,对预测模型进行验证,结果证明了本文所提的基于关联度分析组合法的准确性。
1 最大负荷预测模型
1.1 灰色预测
根据灰色系统理论,将电网最大负荷这一灰色量作为系统特征数据序列,而该地区人口、地区生产总值作为相关因素序列,建立GM(1,n)模型[6-7]:

1.2 BP神经网络预测
根据神经网络理论,在数据输入模块中,将已知数据以矩阵形式输入MATLAB中,A、B代表影响某地区最大负荷的两个影响因素,分别为该地区人口数量、地区生产总值。C表示最大负荷的情况。
其次是数据归一化模块,使用premnmx函数,对数据进行归一化处理,premnmx函数是把数据处理成[-1 1]之间的数据[8],算法为:

即整组数据的最大值为1,最小值为-1,其余数据分布在此区间内。网络训练部分使用MATLAB自带BP神经网络工具箱进行训练,之后利用训练好的BP网络对原始数据进行仿真,并利用postmnmx函数把仿真得到的数据还原为原始数量级。
1.3 基于关联度分析的组合预测
影响最大负荷预测结果的因素有很多,比如该地区人口数量、经济发展情况。而灰色预测与BP神经网络预测都存在自身的局限性,其任一单项模型的预测结果精确度较低,如果按照等权平均的方法对两个模型进行组合,其预测会出现较大偏差,故对这两个模型进行定量关联度分析,确定其各自模型在组合预测中的权重。

关联度r1+r2=1,f1为 灰色GM(1,n)的预测值,f2为BP神经网络预测值,则基于关联度分析的组合预测模型为:

2 算例
利用最大负荷建模的方法,选取某地区2015~2019年最大负荷的实际值作为原始数据,分别建立GM(1,n)模型、BP神经网络模型、基于关联度分析的组合预测模型,其预测结果见表1,拟合精度情况如图1。通过表、图可知,GM(1,n)预测模型、BP神经网络预测模型,拟合误差较大,基于关联度分析的组合预测效果最好,其预测曲线与实际数据曲线基本重合。
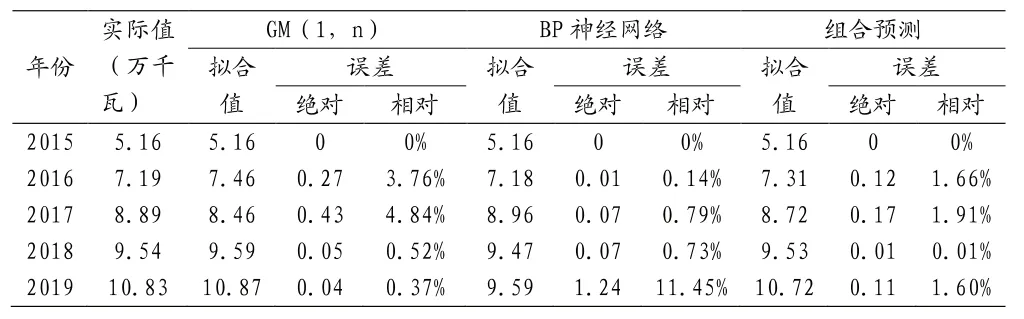
表1 各模型的拟合结果
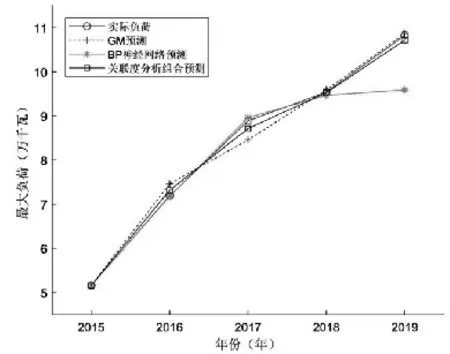
图1 模型的拟合精度情况
2.1 GM(1,n)模型
建立GM(1,n)模型得a=0.5173,b2=0.4952,b3=-0.0408;根据(2)式得灰色GM(1,n)模型:

2.2 BP神经网络
将原始数据仿真的结果与已知样本进行对比,网络训练误差结果可以达到0.01的精度要求,绘制曲线对比仿真结果与实际输出值的情况如图2所示,显然二者非常接近误差极小,故可以对数据进行仿真预测。
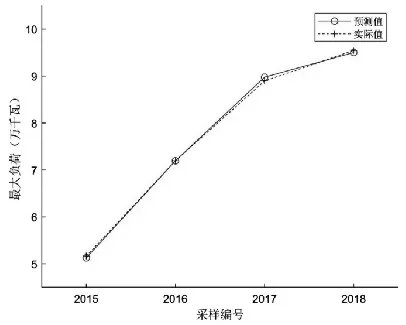
图2 BP神经网络预测值与实际值比较图
2.3 基于关联度分析的组合预测模型
把最大负荷实际值作为参考数列,GM(1,n)预测值和BP神经网络预测值作为比较数列,通过关联度分析后,分别得到GM(1,n)与实际值的关联度r1=0.4585;BP神经网络预测值与地区最大负荷的关联度r2=0.5415,根据式(5)可得预测模型为:

3 结束语
采用关联度分析组合法、GM(1,n)预测模型、BP神经网络模型对某地区电网负荷进行预测。结果表明,本文所提出的预测方法,相比于任一单项预测方法更加精确,其预测曲线与实际数据曲线基本重合,应用于长期负荷预测具有更好的实用性。可以为该地区电网安排运行方式、计划用电管理和电网调度提供科学依据。
