基于物理原始问题的模型建构中实现“减负增效”的策略与实践——以安徽省近年来的中考压轴题为例

安徽省庐江县龙桥镇初级中学(231551) 黄 琴 刘信生

安徽省合肥市教育科学研究院(230071) 陶士金

1 问题的提出

2021年7月24日，中共中央办公厅、国务院办公厅出台了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(以下简称“双减”政策)。这是继2018年末，教育部等九部委颁发《中小学生减负措施》之后，又刮起的针对减少中小学学生学业负担的旋风。单靠“刷题”过关的时代会成为过去吗？当前那些只注重计算和推演的物理习题是经过命题者精心简化抽象后再进行赋值处理得到的，持有“要想学得好，习题必多做”的观点的人只注重“双基”的低档次能力的重复训练，这是缘木求鱼、舍本逐末的做法，这种选拔人才的方式危害极大，与当下落实物理学科核心素养的培养目标严重不符。要想打通“双基”到“核心素养”的任督二脉，我们的教学必须做到知识结构化、任务情境化和学习实践化，大力提倡基于原始问题的教学是解决问题的出路所在。这也是多年来，安徽省物理中考试题命制中一直追求的重要导向——注重考核学生解决原始问题的能力。

2 原始问题的模型建构法解决策略

原始物理问题是自然界及社会生活、生产中客观存在且未被加工的典型物理现象和事实，是未被分解、简化、抽象的，能够直接反映最真实的物理生活情境的现象或问题[1]。物理原始问题是物理习题的上位概念，是文字描述性的物理现象中的问题，其作用主要体现在依靠学生发现问题的本质，对问题进行抽象分析和处理，建构科学的物理模型，有步骤地培养学生解决实际问题的科学思维能力，其两者关系如图1所示。以下就安徽省近年来物理中考压轴题展开基于物理原始问题的模型建构教学分析，以便大家交流讨论。

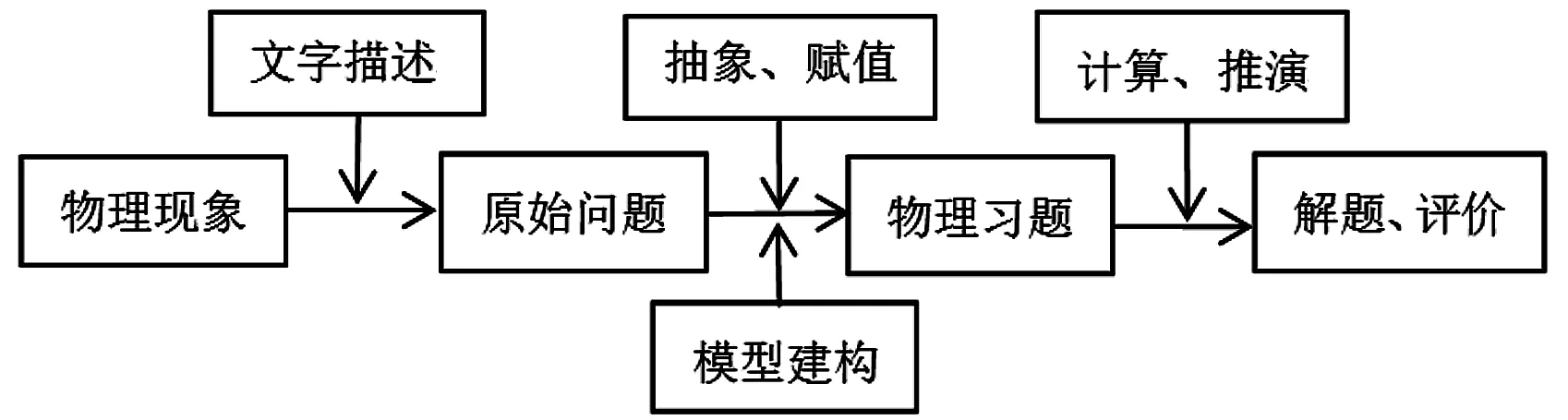
图1 原始问题和物理习题之间的关系

3 模型建构在解决原始物理问题中的应用实例

3.1 从“铅球是用铅制成的吗？”引发学生模型建构能力的形成

中考题1(2008年)：上体育课时，同学们在投掷铅球时，为铅球到底是用什么材料制成的争论起来。小东说：“铅球就是用铅做的，要不然为什么叫它铅球呢？”小兵说：“不对。我仔细看过体育用的铅球，它的表面很硬，像是铁做的。若是用铅做的会比较软，容易被划伤。”两个人谁也不服谁，请你设计实验，如何进行鉴别？

学生遇到这样的题目，第一反应就是想办法测量铅球的密度，然后将测得的密度值与密度表中铅的密度值进行比较即可。那么问题来了，所需的测量工具是什么？如何进行测量？

学生甲：用实验室里的托盘天平和量筒。

学生乙(略加思索)：不行呀，铅球体积和质量都较大，质量已超过托盘天平量程，也无法将铅球放入量筒中去测量体积。

师：乙同学说的对，那么在测量工具的选择上有没有其他更好的办法呢？学生陷入深思之中。

3.1.1 测量铅球的体积

请同学们从图2中选出合适的测量工具和器材来进行实验，引导学生思考用细线和刻度尺进行测量，有什么不妥吗？是否可以用量筒直接测出铅球的体积，如果不能，又有什么好的办法？

图2 生活中的一些测量工具和器材

可以选取塑料桶、量筒(量程为1 000mL)和水等器材，间接测出铅球的体积吗？可以直接把铅球放入装满水的塑料桶里测出溢出水的体积吗？怎样才能减小实验误差？说说具体的实验步骤。学生在上述问题的引领下，通过任务驱动法有步骤地展开探究。

教师发挥指导性作用，师生在交流讨论中一致认为必须增加生活中的一些器具。学生发现测量质量的仪器比较好解决，例如可以用超市用电子秤(磅秤)，但是针对铅球的体积测量学生提出较多的想法，最后一致认为采用间接测量法。教师将学生的设计方法进行分类，总结为以下两类模型：①将塑料桶和量筒配合起来测量铅球体积；②将细线和刻度尺配合起来测量铅球体积。师生再对这两种方案进行评估，对这两种方案的误差进行预判，最后发现模型①是一个合适的方法。物理实验的设计过程，实质上也是模型建构的过程，在科学思维能力的发展过程中解决物理问题是建模的本质特征。师生共同参与，通过密度的测量来对铅球进行鉴别。

3.1.2 测量铅球的质量

选取量程较大的电子秤，先阅读使用说明书，再用电子秤称出铅球的质量。

3.1.3 算出铅球的密度

根据密度的定义式ρ=m/V算出学生铅球的密度，与教材中密度表上的数值进行比对，密度明显小于铅的密度，说明学生铅球根本不是用铅制作的。

正如杨振宁教授所说的，物理学最重要的部分一定是与现象有关的，绝大部分物理学是从现象中来的，现象是物理学的根源．而原始物理问题恰是一种与物理现象对应的具备可操作性的物理教育方式。由原始问题开始，逐步找出其中的本质，建构模型后对相应的物理量进行赋值，计算和推理得出结论，这一过程使学生首次尝试原始问题的解决路径，培养了学生的学科素养。

3.2 从“家用电器实际功率问题”强化学生物理建模思想的巩固提高

中考题2(2010年)：“在家庭电路里，为什么在用电高峰的傍晚开灯时，灯显得较暗，而深夜时开同一盏灯，为何又显得很亮呢？”

这是一道典型的只有文字描述的物理原始问题，要想引导学生求解出结论，只有通过阅读试题，找到教材中的关联知识，抽丝剥茧出已知量和未知量之间的联系，从问题的本质中创设问题情境，在情境中建构家庭电路物理模型，通过实验探究，得出实验结论和反思评价。

教师发现这一类型的题目本质上是考察与电器的“实际功率”相关的问题，这里面没有家庭电路模型，更没有一个用电器的包括铭牌在内的相关赋值，想要靠简单的语言描述把题目的原委讲清楚是做不到的。所以首先想到带领学生在拆解问题中抽象出物理量后建立物理模型：

(1)同学们能建立家庭电路模型吗？(不可以，家庭电路电压220 V，对学生有人身危险，而且不宜在实验室里分组实验，只有用小灯泡的电路模型代替。)

(2)在输送电压不变的情况下，用电高峰期和用电低峰期灯泡亮度不一样的原因是什么？(主要是因为输电线有电阻存在，用电高峰和用电低谷时输电线上流过的电流不同，输电线上分压大小也不同，导致灯泡实际电压发生变化。)

(3)同一盏灯泡的亮暗，其实际电压与实际功率有何关系？(用电器实际电压越低，实际功率越小，灯泡越暗，反之亦然。家庭电路中傍晚时的实际电压应该低于深夜的实际电压，是导致出现这种现象的原因。)

(4)如何去赋值、演算和推导？(用学生电源、灯泡、电流表、电压表等来模拟家庭电路，建构表格模型，计算实际功率后推演，得出结论并反思评价。)

基于以上思路，师生共同选择实验器材，连接实物电路，展开探究活动。

师：为了能够方便进行分组实验，同学们，在器材选择上有何建议？

生：根据题目要求，为了能够测量用电器“实际功率”，必须要用电流表测实际电流、电压表测实际电压，用电器就用“2.5V 0.3A”普通小灯泡若干个充当，当然少不了学生电源、滑动变阻器和导线若干。

师：很好，下面就如何构建“家庭电路模型”动手操作吧！

我们选一个具有代表性的实物电路图模型，如图3所示，用学生电源(用6 V供电)来模拟发电厂或者变压器；用串联在干路上的定值电阻R线(用滑动变阻器代替，接入电路部分阻值约5 Ω)来模拟长途输电线的电阻；用6只小灯泡且由开关各自控制的并联电路模拟家庭电路。整个“家庭电路”的架构装备完成。

图3 “家庭电路”实物模型

教师引导学生画出“家庭电路”实物模型的电路图，并运用等效法进行点拨：将6个同型号的小灯泡并联电路看成一个整体，等效成一个电阻R总，那么，整个模拟电路可以看成长途输电线电阻R线和家庭总负载R总相串联的简单电路，如图4所示。

在一切准备就绪的情况下，师生共同展开实验探究，依次改变电路中连接的用电器数目的多少，记录数据，计算出每一盏灯泡的实际功率，得出正确的实验结论。

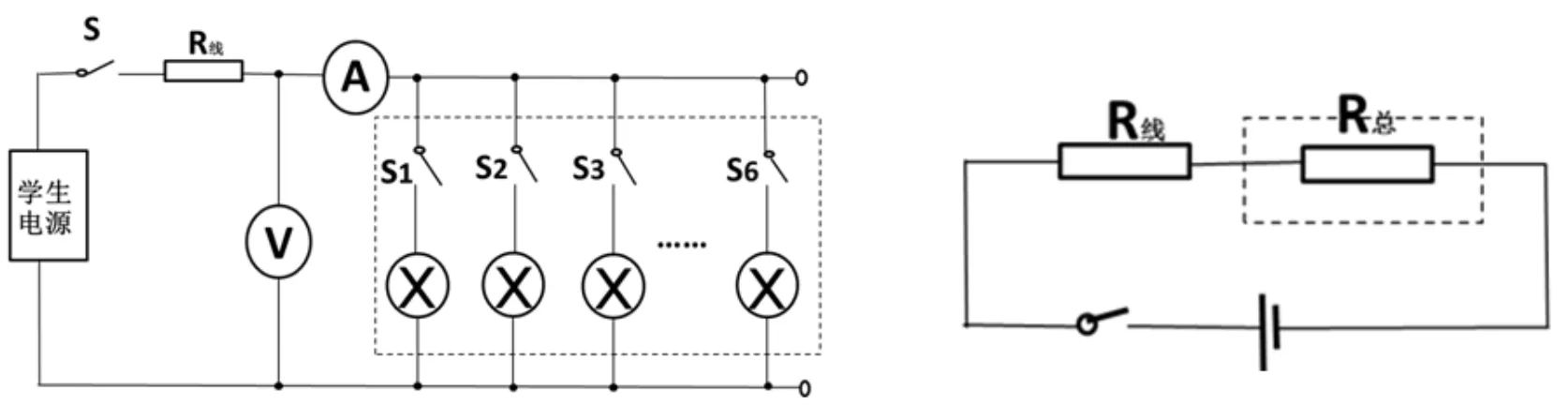
图4 “家庭电路”实物模型的电路图

①只闭合开关S，电流表示数为0，电压表示数为6 V，再依次闭合S1、S2……S6，分别读出各自对应的电流表和对应的电压表示数，记录在表1中；②根据公式R=U/I计算出“家庭电路”中所有用电器的总电阻R总，再运用P=UI算出不同情况下对应电路中每一盏灯泡的实际功率P。

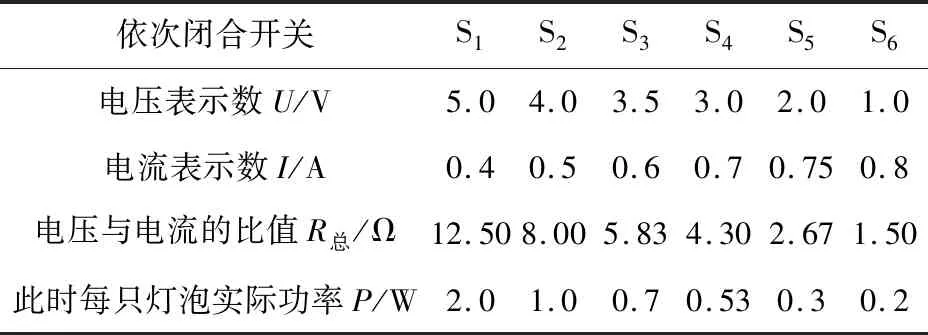
表1 依次闭合开关时电流表和电压表的示数以及电阻和实际功率数据

至此，我们可以得出结论并分析评估，由于并联导体(小灯泡)的电阻随着并联导体的增加会变小的道理，发现家庭电路内部的总电阻随着工作的用电器数目的增加而减小，家庭电路内部的实际电压是减小的，每一盏灯泡上的电流也是减小的(忽略灯泡电阻随温度的变化而变化的因素)，家庭电路总电流在增大。当6只灯泡同时接通时，长途输电线的电压由U=IR得出，输电线上分得电压是最大的，家庭电路内部分得电压最小。由迁移理论可知，在真实生活中，傍晚时分，所有家庭电路中用电器都处于工作状态，每家每户的进户线电流达到最大值，长途输电线上的电流也是迅速增大，而变压器输出总电压不变，输电线分得电压会剧增，导致家庭电路内部的电压明显低于额定电压220 V，家用电器实际功率低于额定功率也就不足为奇；反之，深夜时刻，家用电器使用量锐减，家用电器上分得的实际电压偏高，家用电器实际功率高于额定功率。

我们在具体的情境设置中巧妙构建适当模型进行深入分析，终于弄懂“傍晚灯暗，深夜灯亮”的原委。这里有人说用定值电阻来模拟家庭电路，笔者感觉不妥，用小灯泡来实验就是方便学生在探究过程中能“高见度”地看到整个实验现象，有视觉冲击力，何乐而不为。通过实例进一步说明了物理模型建构的过程就是在研究物理问题，要突出研究对象的主要因素，忽略次要因素。

3.3 从“杠杆的平衡条件问题”促进学生物理建模能力的升华

中考题3(2021年)：

(1)如图5(a)，一质量分布均匀的杠杆，忽略其厚度和宽度，不忽略长度，用细线将其从中点悬起，能在水平位置平衡。将它绕悬点在竖直面内缓慢转过一定角度后放手，如图5(b)，请将两边的力和力臂作出，用杠杆平衡条件证明在该位置仍能平衡。

(2)如图5(c)，一质量分布均匀的长方形木板，忽略其厚度，长度和宽度不忽略，仍然从木板的中点悬挂起来，按照问(1)中要求缓慢转过一定角度，如图5(d)，还能在该位置平衡吗？写出判断依据。

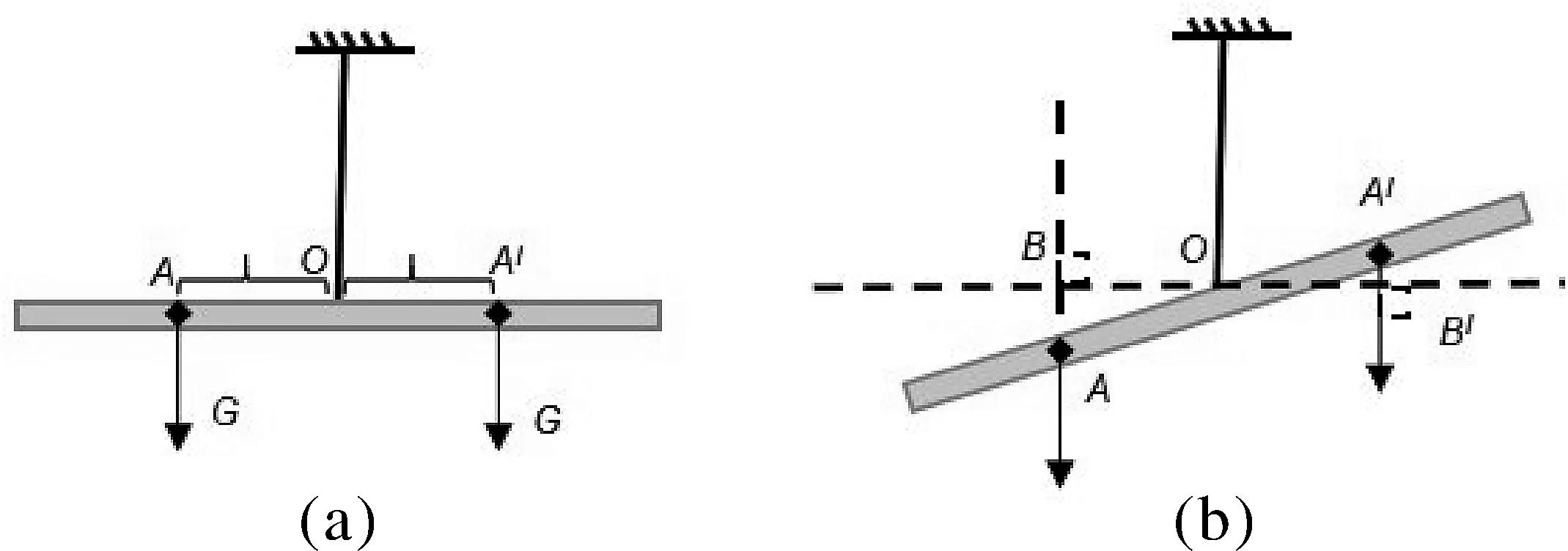
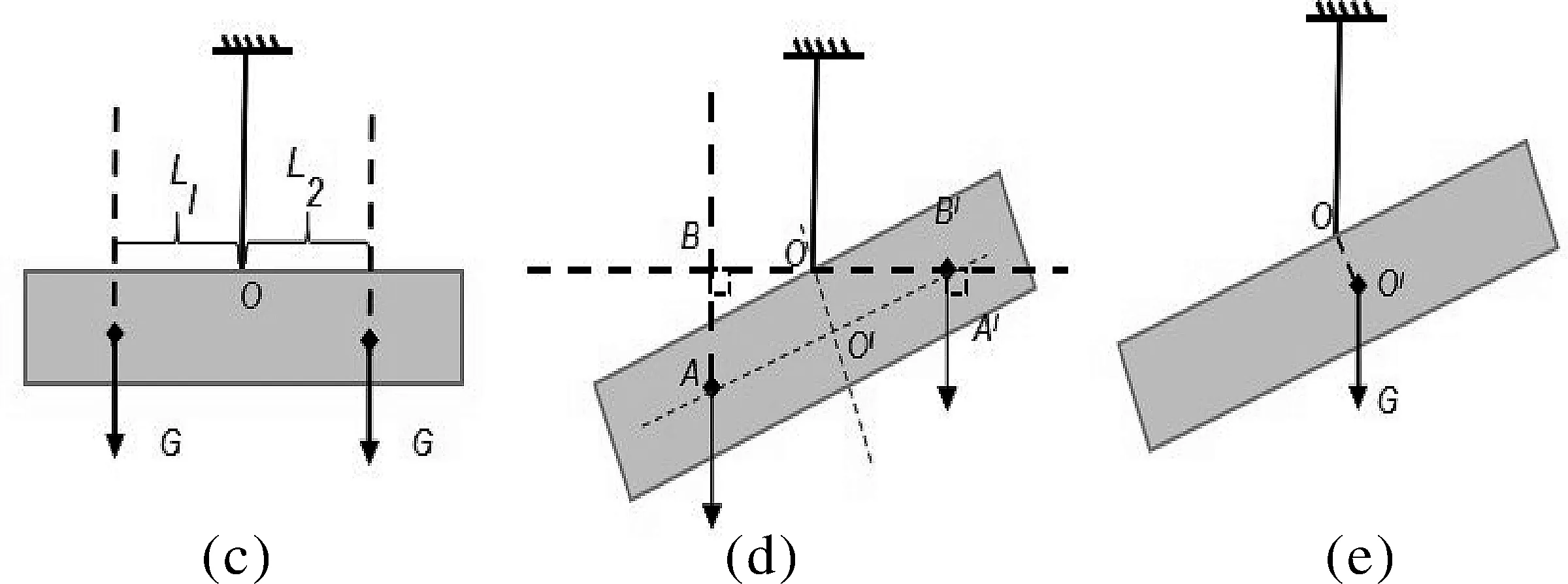
图5 “杠杆的平衡条件问题”图示

这道试题是很地道的原始问题，整道试题只有描述物理现象的语言，与物理原理和物理量相关的内容只字未提，该题是在抽象出杠杆平衡原理的基础上重点考查学生的杠杆模型建构能力，要求学生能够整合关联知识，应用物理原理进行赋值推演，得出结论，解决实际问题。学生分析可得：问(1)中忽略杠杆的厚度和宽度等次要因素，只考虑杠杆的长度因素，由于其质量均匀，我们从支点处将杠杆分为等长的两部分，两部分重心到支点的长度相等，重力方向竖直向下，与水平杠杆垂直，两边的力臂就等于重心到支点的长度，即图5(a)中有OA=OA′，G·OA=G·OA′，杠杆满足平衡条件；再将杠杆缓慢转过一定角度后，在图5(b)中分别画出杠杆左右部分受到的重力和力臂的大小的示意图，由图5(b)知在△AOB和△A′OB′中，因为OA=OA′，∠AOB=∠A′OB′，AB⊥OB，A′B′⊥OB′，由三角形全等条件可以得出△AOB≌△A′OB′，则有OB=OB′，这时候也有G·OB=G·OB′，此时杠杆仍然可以平衡。

在问(2)中，忽略长方形木板的厚度，长方形板的长度和宽度不忽略，我们可以建立平面杠杆模型。由于长方形木板是对称图形，图5(c)中有L1=L2，G·L1=G·L2，杠杆满足平衡条件；将杠杆缓慢转过一定角度后，此时杠杆两边重力的力臂发生了变化，如图5(d)所示，杠杆左边的力臂为OB一定小于木板中心O′到左边部分重力作用点A的距离O′A，即OB

问(2)也可以运用二力平衡模型进行简单的判断，由于质量均匀的木板的重心在其几何重心O′(长方形对角线的交点)，如图5(e)所示，显然在水平位置时木板受到的重力和绳子向上的拉力满足二力平衡原理，木板能保持水平平衡，当木板缓慢用力转过一定角度后，木板的重力作用线发生水平偏移，其受到的两个力不再满足二力平衡条件而成为一对非平衡力，故木板一定会发生转动而不再平衡了。同理，问(1)因忽略了杠杆的厚度和宽度而只考虑其长度，所以无论杠杠是否绕支点发生偏转，其重心始终位于支点的正下方，杠杆仍然受平衡力作用而静止，杠杆不发生转动。

4 结语

国家实施“双减”政策，实际上是对教育教学的一种纠偏，是对过去“知识核心时代”以纸笔式的低档次、重复式、机械性传统习题训练的一种纠偏。“核心素养时代”的原始问题教学，加强物理模型建构教学过程中的科学思维培养显得尤其重要。运用原始问题对学生进行核心素养水平的评价更能体现科学思维素养，但必须注重原始物理问题与习题的转化[2]。因此，适当地凸显物理原始问题的教学，将原始物理问题情境融入到学生已有的知识体系中，实现在发现问题中学习有用的知识，在解决问题中发展真正的能力，在实践创新中培养学科核心素养，也是回应国家在“双减”政策下学生作业模式改革的热点。