基于变形数据的古塔数学建模

秦春影

（南昌师范学院 数学与信息科学学院，江西 南昌 330032）

古代建筑具有很强的历史和科研价值，今天很多的研究都需要借助古代建筑作为辅助，如一些史实的验证，古文明的发展过程和历史等.古塔因其特殊的结构和作用而更加宝贵，流传至今的古塔的保护十分重要，而充分了解古塔当前的状态是有效保护的前提条件.流传至今的古塔受限于当时的科学技术和建筑手段，或多或少存在一些问题[1-4]，如塔基所在地质的不稳定，这种情况下的古塔想保存下来非常不容易.对古塔的损害最常见的是地基的不均匀沉降，从而导致塔体倾斜甚至扭曲[5-6]；还有就是人为破坏（如战争等）和自然灾害[7]所导致的损坏，这些不同类型的破坏对古塔本身都会造成不同程度的损害，有些损害是不可修复的，还有些损害是可以修复的，或者说可以减缓对塔的损害.近年来，古塔的修复和保护工作受到社会的广泛关注和重视，但是古塔的修复工作是一项系统性的工作，本身的复杂性远远超出外界的想象，修复和保护的方法不科学甚至会加剧古塔的破坏，加快古塔的消亡.本文通过对已有数据的分析，对古塔各层的缺失数据进行合理的填补和恢复，在此基础上对各层的中心进行定位，从而判断古塔本身随着时间按何种趋势发生变化，为古塔的保护和修复提供科学依据.

1 古塔缺失数据的插补

古塔的层中心对于古塔的修复和积护非常重要，但是由于年代久远，导致造成数据缺失较为严重.如何在包含缺失数据的情况下确定古塔的层中心是本研究关注的核心问题，而这里面最关键的问题之一就是对缺失数据的填补或恢复[8-10].以某古塔为例，收集到1986 年7 月，1996 年8 月，2009 年3 月和2011 年3 月对该塔的4 次测量数据，部分测量数据见表1.该古塔一共有13 层，表1 中只是提供了1986 年和1996年的第1 层的数据，共测量了8 个点的数据，其中x，y，z分别为每个测量点的坐标，每一年的测量数据中还包括塔尖的4 个测量点的数据，限于篇幅，其余各层的数据以及2009 年和2011 年的数据不再列出.

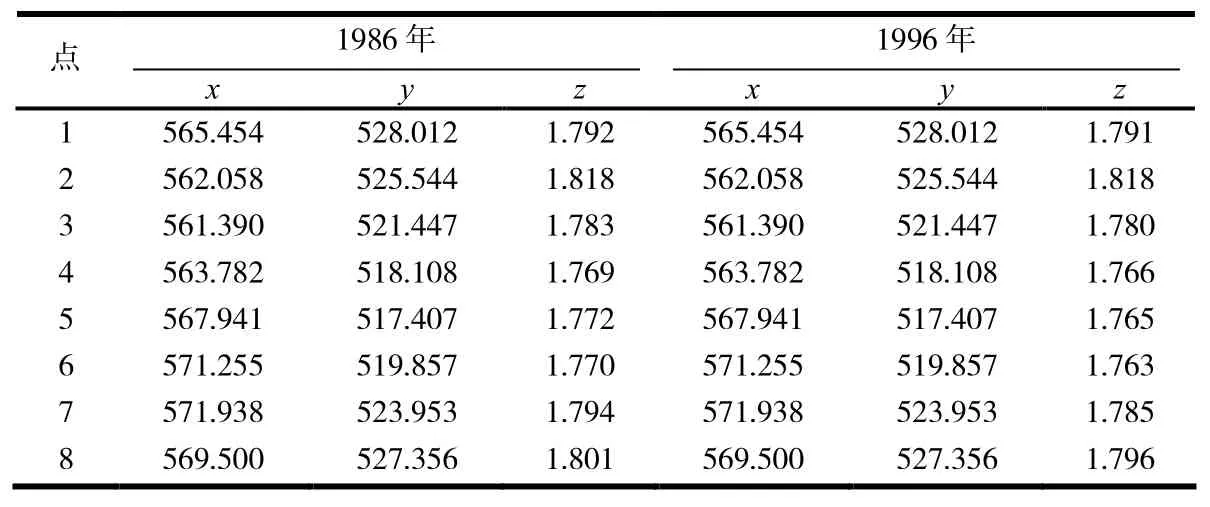
表1 1986 年和1996 年第1 层的观测数据

由于所给出的数据中缺少1986 年和1996 年第13 层的第5 个测量点的数据，缺少2009 年和2011 年塔尖的第2，3，4 个测量点的数据，因此，需要对缺失的数据进行处理.

对于1986 年和1996 年第13 层第5 个测量点的缺失数据，数据处理的出发点是：每一层的第5 个测量点之间应该具有某种关系，分别绘出前12 层的第5 个测量点各个坐标的散点图，发现y坐标、z坐标分别近似在一条直线上，因此，可以做出假设，即第13 层的第5 个测量点的y坐标、z坐标也应该分别在各自的直线上.x坐标虽然不是在一条直线上，但是也可以通过类似的方法得到.这样就可以得到1986 年和1996 年的第13 层的缺失数据（见表2）.

表2 1986 和1996 年第13 层补充缺失后的数据

对于2009 年和2011 年塔尖的第2，3，4 测量点的缺失数据，数据处理的出发点是：因为塔尖相对来说是面积比较小的一块区域，所以可以假设这块区域的各个测量点之间的相对位置不会随着时间的变化而变化，即各测量点之间的相对位置是固定的.通过这种思路可以得到2009 年和2011 年塔尖的缺失数据，补充的缺失数据见表3.

表3 1986 和1996 年塔尖的数据

在对缺失数据补充完整后，可以绘出该古塔的三维立体图，1986 年该古塔的三维立体图见图1.

图1 1986 年该古塔的三维立体图

由图1 可以看出，每一层的8 个测量数据正好可以看作是古塔的8 个顶点，该古塔的每一层都是一个八边形.对于每层层中心的计算问题，首先，假设该古塔是由均质的物质建成的，这样才可能计算出该塔各层的中心；其次，通过对数据的分析可以发现，每一层8 个点的z坐标很接近，因此假设这8个点是处在同一平面上，这样各层中心的计算问题就转化为计算由8个点构成的八边形的中心问题.由于这8个点构成的平面可能不是正八边形，因此，不能直接运用正八边形的中心计算方法，这里考虑采用不规则平面图形的中心计算方法.

2 古塔层中心的计算

根据平面解析几何相关的知识可知，如果三角形是由均匀材料做成的，那么几何中心也就是质量中心.它的中心坐标是3个顶点的坐标算术平均值.也就是说，如果顶点a，b，c的坐标分别为（x a,ya），（x b,yb），（x c,yc），那么该三角形的几何中心的坐标为

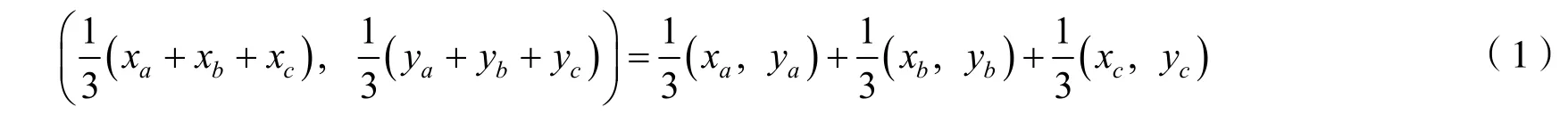
根据假设，古塔是由均匀材料构成的，因此可以使用式（1）来计算中心.

这里每一层测量了8 个点，由这8 个点构成的八边形可以看成是由几个简单基本图形组合而成的，在计算它们的中心时，可先将其分割为几块基本图形，计算机出每块图形的形心位置（x i,yi）与面积Ai，然后利用形心计算公式求出整体的中心位置.

不规则平面图形的中心坐标公式为

通过对数据的分析可以发现，每一层上的8 个点的坐标按顺序连接可以连成一个八边形.以1986 年第1 层数据为例进行说明（其它各年、各层的数据可以按类似的方法来处理）.1986 年第1 层8 个点的投影图见图2.

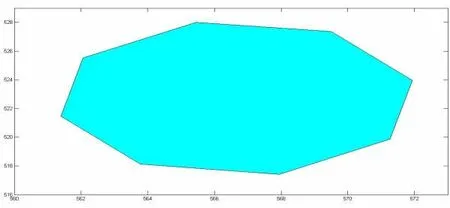
图2 1986 年第1层8个点的投影

将这个八边形进行分割，分割的图形是由6个三角形构成，这样，就可以按照前面介绍的方法来计算各层的中心.

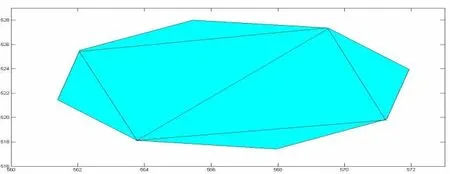
图3 分割后的1986 年第1 层8 个点的投影

分别计算出这6个三角形的中心，然后利用式（1）将这个中心进行合成，合成得到的坐标即为整个图形中心的坐标.

设8个点的坐标分别为（xi,yi）,i=1,2,…,8.先计算出6个三角形的面积，若已知3个顶点的坐标（xa,ya）,（xb,yb）,（xc,yc），则三角形的面积计算公式为

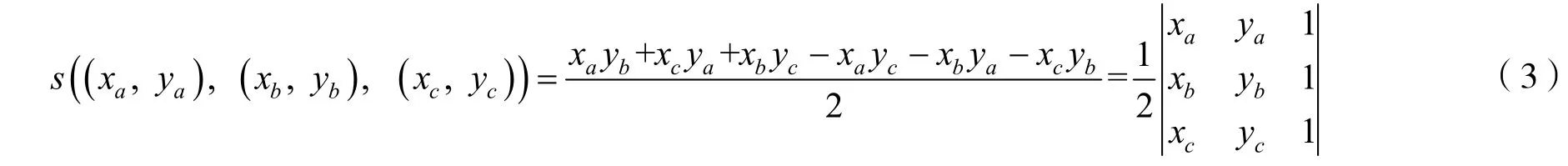
根据式（1）（3）计算出各个三角形的中心坐标和面积，然后利用式（2）对6个三角形的中心进行合成得到各层的中心坐标（x,y,z），其中各层的中心坐标中z值取8个点z坐标的平均值.

1986 年各层的中心和塔尖的中心坐标见表4，其余年份的各层的中心及塔尖的中心坐标可以使用相同的方法计算得到.

表4 1986 年各层的中心坐标

通过这种方法，建立起相应的数学计算公式，在适当的假设条件下，只要给出每层的8个测量点的坐标，编制程序，就可以直接计算出每层的中心坐标.

在解决了确定古塔各层中心的基础上，接下来就根据各层的中心及塔尖中心的偏移情况来计算整个塔身的倾斜、扭曲和弯曲等情况.假设在理想状态下，古塔的各层中心是在一条垂直的直线上，如果随着时间的变迁，古塔各层的中心还在一条直线上，但是这条直线与垂线有一个夹角，这种情况古塔就是发生了倾斜，夹角越大，倾斜越严重；如果古塔各层的中心组成了一条类似于C 形的曲线，则古塔发生了弯曲；如果古塔各层的中心组成了一条类似于S 形的曲线，则古塔发生了扭曲，当然，这只是直观上的分析，具体要判断古塔到底发生了何种变形[11-13]，还需要借助数学上相应的评价指标来判断.通过对古塔的变形，可以预测未来古塔的变形趋势，在此基础上，可以提出对该古塔的修复和保护方案.

3 结语

通过对古塔不同年份测量数据的分析，在一定的假设基础上，对缺失的数据进行了相应的处理.古塔各层测量数据中的缺失数据处理是重要的步骤，如果缺失数据部分处理不好或者不处理直接删除，都会给整个分析的准确性带来较大的损失，进而影响到古塔当前状态及变形趋势的预测，对提出古塔的修复和保护方案产生负面影响[14-15].另外，各层的中心计算是在必要的假设之上的，合理和必要的假设对于数学建模问题的解决也是很重要的[16].因此，对于古塔变形状态的分析必须充分考虑实际情况和测量数据的特点来综合考虑分析方案，这样分析的结果才能对古塔的修复和保护真正起到参考作用.