随机截尾数据下Burr XII 分布参数的Bayes 估计

季海波

（宿迁学院 文理学院，江苏 宿迁 223800）

1 引言及预备知识

在进行可靠性寿命试验时，通常采用截尾试验的方式缩短试验周期，减少试验成本.使用较多的截尾寿命试验有定数截尾和定时截尾，对于这2类截尾情形下的Bayes 估计，已经有了较为完整的结果.除定数截尾和定时截尾试验外，随机截尾情形也经常会用到[1-4].Burr XII 分布在保险精算学、社会科学等很多领域内都有很广泛的应用，在现有的研究结果中，暂时还无人研究随机截尾情形下Burr XII 分布参数的Bayes 估计问题.本文研究了LINEX 损失和复合LINEX 对称损失下Burr XII 分布参数的估计问题.

假设随机截尾试验中受试产品的寿命为X1,X2,X3,…，它们是相互独立且均服从于Burr XII 分布的一列随机变量，对应分布的密度函数和分布函数分别为

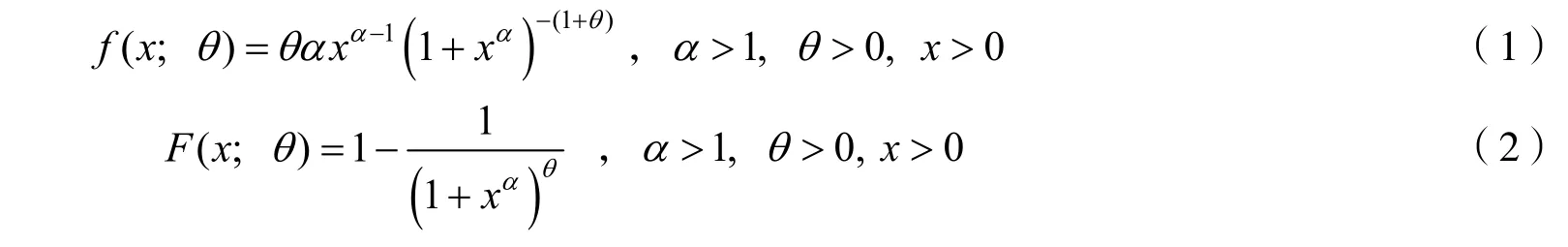
为方便起见，假设其中的参数α已知，θ未知.

将寿命截尾的时间设为一列相互独立的正值随机变量Y1,Y2,Y3,….在实际应用中，由于随机截尾导致试验过程中X i(i=1,2,3,…)无法被完全观察到，仅能观察到min（X i,Yi）和I（X i≤Yi）i=1,2,3,….在随机截尾试验下，记，给定观测值为（x1,σ1）,（x2,σ2）,…,（xn,σn），为了参数估计的存在性，假设.令x=（（x1,σ1）,（x2,σ2）,…,（xn,σn）），那么由式（1）（2）可得随机截尾下的似然函数为

2 参数θ 的Bayes 估计

取参数θ的Jeffreys 先验分布，其先验密度函数为

由式（3）（4）可知，参数θ的后验条件密度函数为

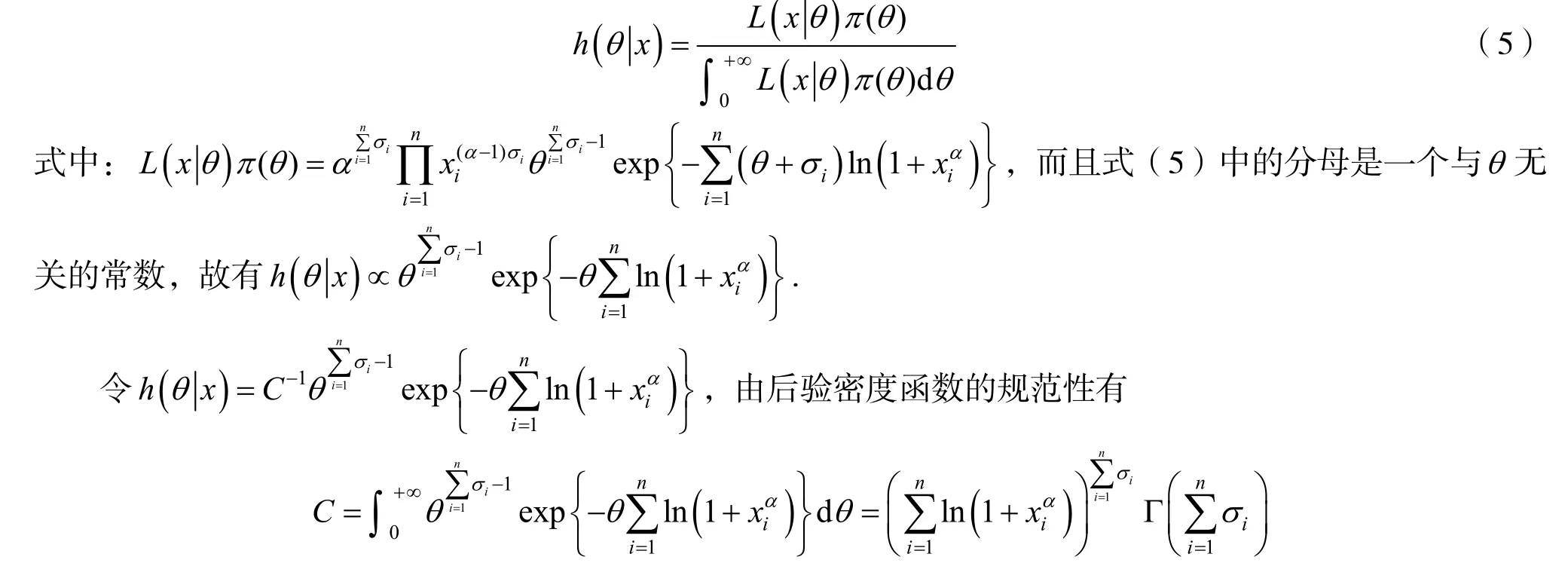
从而未知参数θ的后验密度函数为

定理1在LINEX 损失函数L(θ,δ)=ec(δ-θ)-c（δ-θ）-1(c∊R,c≠0)下，若参数θ取Jeffreys 先验分布，则分布（1）中参数θ的Bayes 估计为

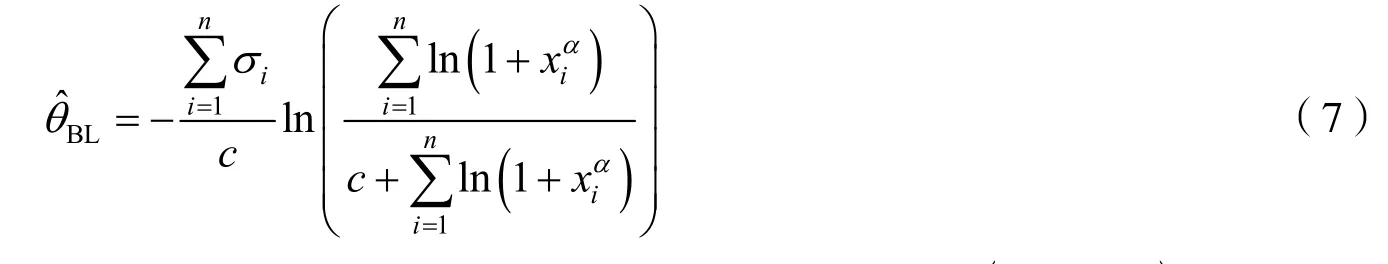
证明由文献[5]可知，在LINEX 损失函数下，参数θ的Bayes 估计为，由式（6）可知

文献[6]提出了复合LINEX 对称损失函数

定理2在损失函数（8）下，若参数θ取Jeffreys 先验分布，则分布（1）中参数θ的Bayes 估计为

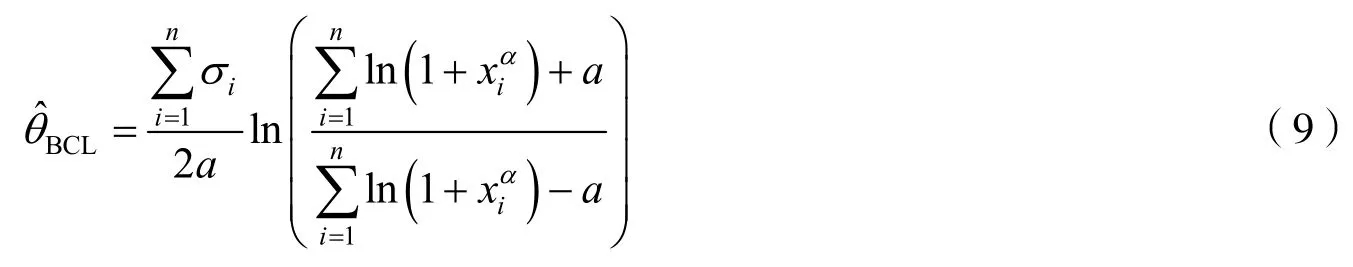
证明由文献[6]可知，在复合LINEX 对称损失函数下，参数θ的Bayes 估计为由定理1 中的结果易知，从而有证毕.

3 随机模拟

由于本文推导的不同损失下的估计都是在α已知的前提下，故利用Monte-Carlo 方法进行模拟前，先取α=2.预先给定每一部件的截尾时间y1,y2,…,yn，利用文献[7]的算法产生随机截尾的样本.利用样本数据及式（7）（9），给出对应损失下的Burr XII 分布参数θ的Bayes 估计.取a=c=1，利用Matlab 编程，随机模拟1 500次，模拟结果见表1.

表1 2 种损失下指标θ 的Bayes 估计模拟值

由表1可以看出，不管是哪种损失函数下的估计，都呈现出样本量越大越接近真值的趋势；相同的真值和样本量的情形下，不管是看均值还是均方误差，都是复合LINEX 对称损失函数下的Bayes 估计较为优良.故在求随机截尾情形下Burr XII 分布参数θ的Bayes 估计时，优先推荐利用复合LINEX 对称损失函数.