关于矩阵多项式的交换性

雷震

（安徽师范大学 数学与统计学院，安徽 芜湖 241000）

1 引言及预备知识

矩阵多项式的交换性是线性代数学科一个重要内容[1-3].设f(x)=a0+a1x+…+a mxm为x的m次多项式，A为n阶矩阵，E为n阶单位矩阵，记f(A)=a0E+a1A+…+amAm，f(A) 是一个n阶矩阵，称为矩阵A的一个m次多项式（参见文献[3]定义2.3.2）.如果AB=BA，根据矩阵相关运算性质，对于矩阵A，B的任意多项式f(A)，g(B)，f(A)g(B)=g(B)f(A) 成立.本文中0 表示零向量或零矩阵.

一个有趣的实例是：如果矩阵A，B满足AB+A+B=0，则AB=BA成立，即对于任意多项式f(A)及g(B)，有f(A)g(B)=g(B)f(A).这个实例的逆命题一般不成立，如，有AB=BA，但.实例的条件等价于(A+E)(B+E)=E.

注意到A+E是矩阵A的一次多项式（B+E是矩阵B的一次多项式），自然地，有如下问题：如果存在矩阵A的一个m（m>1）次多项式f(A)=a0E+a1A+…+amAm，满足f(A)(B+E)=E，是否有AB=BA成立，即对于任意多项式h(A)及g(B)，是否有h(A)g(B)=g(B)h(A).

本文根据环论的相关性质给出上述问题的肯定答复.另外，也指出矩阵A的一个m次多项式如果是可逆的，则其逆矩阵可表示成A的多项式，矩阵A的伴随矩阵A*的多项式及其逆矩阵都可以表示成A的多项式.本文所涉及的环是指有单位元的结合环.

2 主要结果及证明

定理1设R是一个有单位元的结合的交换环，A是R上的一个n阶方阵，如果存在矩阵A的一个m（m>1）次多项式f(A)=a0E+a1A+…+amAm（ai∊R，i=0,1,2,…,m)，满足f(A)(B+bE)=E（b∊R），则有AB=BA成立，即对于任意多项式h(A) 及g(B)，有h(A)g(B)=g(B)h(A) .

证明根据环的定义，容易验证关于矩阵的加法及乘法构成一个环.由于R是一个交换环，所以R[x]是一个交换环，而对于任意非负整数k,l，有A k Al=Al Ak，因此R(A)也是一个交换环.

由于f(A)(B+bE)=E，所以f(A) 是R(A) 中的一个可逆元，且其逆元B+bE∊R(A)，所以B可以表示成A的多项式，因此AB=BA，即对于任意多项式h(A) 及g(B)，有h(A)g(B)=g(B)h(A) . 证毕.

文献[4-9]的研究表明，数域P上的n阶方阵A的多项式f(A) 的逆矩阵（f(A)）-1可表示成矩阵A的多项式.显然，这个结论是定理1 的自然推广.

推论设R是一个有单位元的结合的交换环，A是R上的一个n阶方阵，如果A的一个m（m>1)次多项式f(A)=a0E+a1A+…+amAm（ai∊R，i=0,1,2,…,m)是可逆的，则f(A) 的逆矩阵（f(A)）-1可表示成矩阵A的多项式.

显然，数域P是一个交换环，所以将定理1 中的交换环R换为数域P，结论也是成立的.对于这个结论，根据哈密尔顿-凯莱定理给出另外的证明，以方便只学习过线性代数理论，而没有学习过环模理论的读者也能理解.

定理2设P是一个数域，A是P上的一个n阶方阵，如果存在矩阵A的一个m（m>1)次多项式f(A)=a0E+a1A+…+amAm（ai∊P，i=0,1,2,…,m)，满足f(A)(B+bE)=E（b∊P)，则有AB=BA成立，即对于任意多项式h(A) 及g(B)，有h(A)g(B)=g(B)h(A) .

证明记是矩阵f(A) 的特征多项式，根据哈密尔顿-凯莱定理可知，φ（f(A)）=，这里c1,c2,…,cn-1为系数，由于f(A)是可逆矩阵，所以，f(A) 的逆矩阵即B+bE可以表示成f()A的多项式，因此B可以表示成A的多项式，进而有AB=BA成立，即对于任意多项式h(A) 及g(B)，有h(A)g(B)=g(B)h(A) . 证毕.

在定理1～2 中，B+b E只是矩阵B的一次多项式，当将B+b E改为二次及以上次的多项式时，定理结论未必成立.

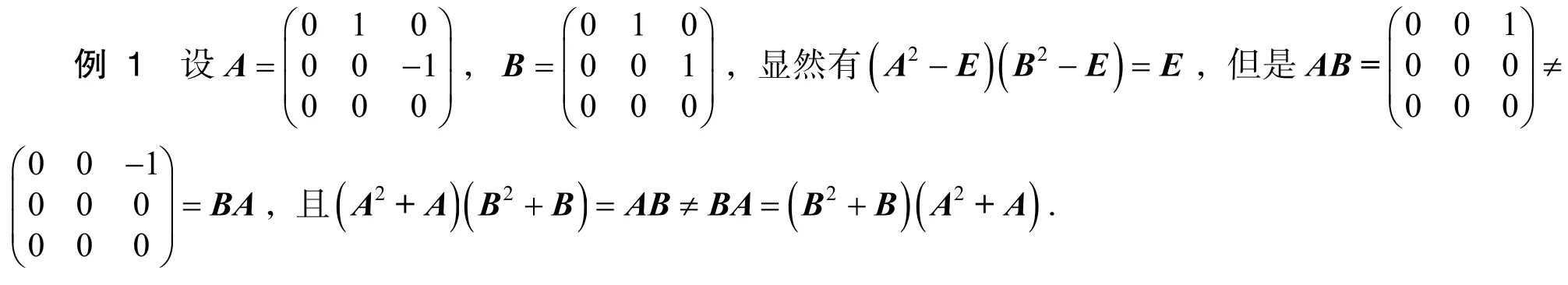
例1表明，AB=BA只是矩阵A及B的某些多项式可换的充分条件.

文献[10]根据线性空间理论证明了：设A是数域P上的n阶方阵，则A的伴随矩阵A*可表示成A的多项式.本文利用线性方程组解的理论给出这个结论的证明.

引理设A是数域P上的一个n阶方阵，且A的秩为n-1，如果AB=BA=0，B≠ 0，则存在齐次线性方程组Ax=0的一个基础解解系α，及ATx=0的一个基础解解系β，使得B=αβT.

证明由于rank(A)=n-1，而AB=0，所以rank(A) +rank(B)≤n，而B≠0，所以B的秩为1，因此，存在非零的n维列向量α,β，使得B=αβT，又由于0=AB=AαβT，所以Aα=0，即α是齐次线性方程组Ax=0的一个基础解解系.同理，由于0=BA=αβTA，而α是非零的n维列向量，所以βTA=0，即有ATβ=0，所以，β是齐次线性方程组ATx=0的一个基础解解系. 证毕.

定理3设P是一个数域，A是P上的一个n阶方阵，A*是A的伴随矩阵，则f（A＊）及 （f（A*））-1都可以表示成A的多项式.

证明记，根据定理1 的证明，只需要证明f（A*）∊P(A)，即只需要证明A*∊P(A).

假设rank(A)＜n-1，则A*=0∊P(A).

假设rank(A)=n-1.由于，根据引理可知，A*=αβT，这里α,β是非零的n维列向量，且α是齐次线性方程组Ax=0的一个基础解解系，β是齐次线性方程组ATx=0的一个基础解解系.记A的特征多项式为f(x)=a0+a1x+…+an-1xn-1+xn，根据哈密尔顿-凯莱定理可知，f(A)=a0E+a1A+…+an-1An-1+An=0，由于rank(A)=n-1，即A不可逆，所以a0=0，即有A（a1E+…+an-1An-2+An-1）=（a1E+…+an-1An-2+An-1）A=0.由引理可知，a1E+…+an-1An-2+An-1=ηγT，这里η,γ是非零的n维列向量，且η是齐次线性方程组Ax=0的一个基础解解系，γ是齐次线性方程组ATx=0的一个基础解解系.由于rank(A)=n-1=rank （AT），所以Ax=0的基础解系与ATx=0的基础解系都只含一个非零向量，因此存在非零数k1,k2，使得k1η=α，k2γ=β，即有k1k2（a1E+…+an-1An-2+An-1）=A*，所以A*∊P(A) .

假设rank(A)=n.由于，因此A的逆矩阵是，根据推论可知，A*可以表示成A的多项式. 证毕.

3 结语

矩阵的交换性是矩阵理论重要的研究内容，本文给出的2 个矩阵多项式乘积可换的充分条件是2 个矩阵的乘积是可换.当2 个矩阵不可换时，其对应的矩阵多项式是否一定不可换，满足什么条件的乘积不可换的2 个矩阵，其对应的矩阵多项式是可换的等问题有待于进一步的讨论.