六相永磁同步发电机系统的零序电流抑制策略
2022-08-12施国栋王侯清何坚强张春富
施国栋,孙 磊,王侯清,何坚强,张春富
(1.盐城工学院,盐城 224051;2.清华大学 精密仪器系,北京 100084)
0 引 言
永磁同步电机凭借其结构简单、能量密度高、控制性能好等优点,被广泛应用于传动以及发电领域[1-2]。当涉及到大功率应用时,由于开关设备耐电压有限,传统的永磁同步电机结构应用将受到限制。为了解决这个问题,1989年日本学者Isao Takahashi提出的一种将定子侧中性点打开的绕组连接方式[3],该连接方式将定子绕组分别连接两个变流器,电机运行时,两变流器同时工作各自分担一部分功率,从而降低对功率器件的容量要求。
开绕组电机系统根据两台变流器是否共用一个直流侧可以分为隔离直流母线和共直流母线两种结构[4]。共直流母线结构相较于隔离直流母线结构在硬件上少了两条需要电气隔离的直流母线,拥有更高的功率密度。然而,两变流器直流母线并联,两变流器之间存在零序回路。此时,变流器中功率器件在高频工况下产生的共模电压和由于永磁体转子结构带来的三次谐波反电动势,便在零序回路上产生零序电流[5],从而额外导致电机的损耗和发热,降低了系统运行的效率和稳定性。
抑制零序电流的方法主要分为硬件和软件两类,硬件主要为在共用的直流母线上增加辅助开关,软件方法只需对变流器的调制策略或控制方法进行改进,无需增加额外的硬件电路,适用于高功率密度的应用场合。文献[6]在空间矢量调制中选择共模电压为零的矢量来达到抑制零序电流的目的,但此时电压利用率减少了15%。文献[7]通过重置矢量有效位置来控制开关周期内共模电压为零。但该方法未考虑到零序电流中存在的三次谐波反电动势,导致无法有效抑制零序电流。文献[8]增加了一个零序电流控制环,通过控制共模电压来抵消三次谐波反电动势,从而达到零序电流抑制的效果。但该方法只适用于三相,在六相开绕组永磁同步发电机(以下简称OW-PMSG)中还存在5次,7次谐波需要抑制。
针对六相OW-PMSG零序电流抑制方法存在的不足,本文提供了一种适用于六相OW-PMSG 改进型零序电流抑制方法。利用控制共模电压抵消三次谐波反电动势的思想,引入比例谐振器,实现对零序电流抑制。同时,改进基于传统四矢量的空间矢量脉宽调制方法,根据参考电压矢量所在的扇区,重新选择矢量并计算对应的作用时间,从而在抑制零序电流的同时,保持对5次、7次谐波的有效抑制。
1 OW-PMSG系统数学模
1.1 OW-PMSG模型
图 1为共直流母线六相永磁同步发电机系统结构,两变流器的每相桥臂中点和OW-PMSG的定子绕组两端连接,两变流器母线直接相连。
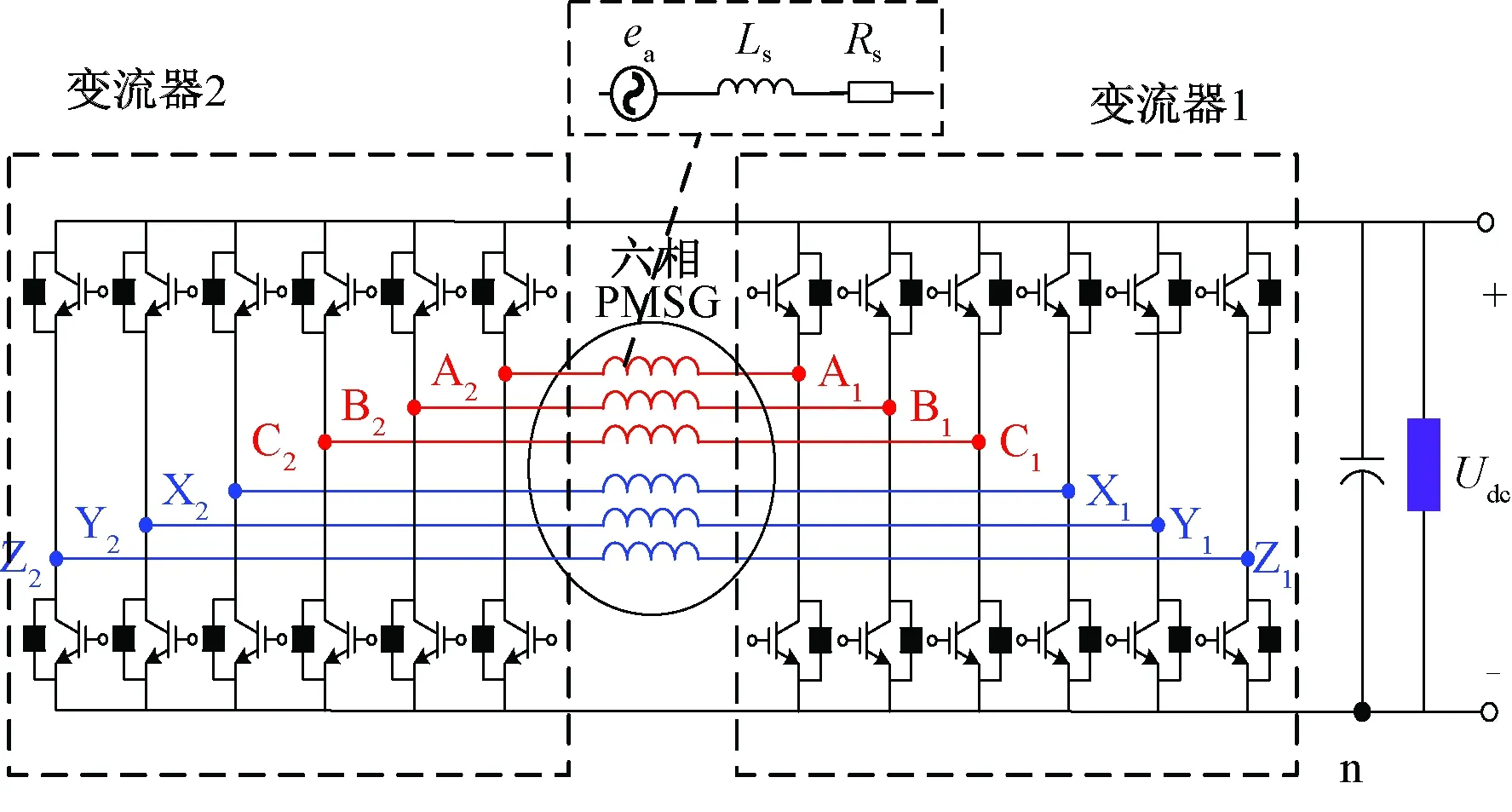
图1 OW-PMSG系统结构
若取n为参考地,可以得到在静止坐标系下,六相开绕组永磁同步发电机系统数学模型:
(1)
式中:e,u,i,Rs和Ls分别代表定子相绕组反电动势、交流侧相电压、交流侧相电流、定子电阻和自感;下标x分别表示OW-PMSG定子六相绕组;下标1、2表示变流器1和变流器2。
对式(1)进行空间矢量坐标解耦变换,可以变换到如下三个正交的二维子空间中[9]:
(2)
(3)
(4)
式中:ωe为同步电角速度;下标α,β,z和o分别表示子空间轴上的分量。
1.2 OW-PMSG系统共模电压与零序电流分析
由于调制方法选择了空间矢量脉宽调制,所以在两变流器上会产生高频的共模电压。在OW-PMSG系统中两变流器共模电压可分别描述如下:
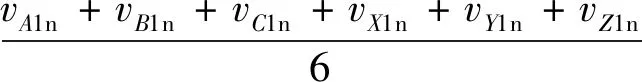
(5)
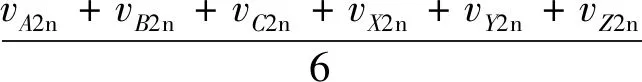
(6)
式中:vcmv1、vcmv2表示两变流器共模电压值;vxn(x=A,B,C,X,Y,Z)表示相电压;Sx(x=A,B,C,X,Y,Z)表示功率器件开关状态;下标1,2表示变流器1和变流器2;Udc表示直流侧电压。
两变流器所产生的共模电压和三次谐波反电动势在零序回路中产生零序电流,在OW-PMSG系统中零序电流回路表达式:
(7)
式中:u0表示零序电压。
2 改进的零序电流抑制策略
为抑制OW-PMSG系统中的零序电流和5次、7次谐波,需要对有效电压矢量和零矢量进行合理的选择和分配。根据式(4)和式(7),抑制零序电流的关键在于对u0的控制,在此我们选择u0等于0的电压矢量,来保证在有效电压矢量工作期间共模电压在零序回路中无电流产生,而零序回路中3次谐波反电动势部分则由零电压矢量中的共模电压来抵消,从而保证在一个开关周期内零序回路中无电流产生。再此基础之上,只需要控制合成的电压矢量在z1-z2子空间投影为零,即可完成对5次、7次谐波的抑制。
六相OW-PMSG系统之中共有24个开关管,共可以产生4 096种开关状态。根据上文的调制策略,可以对所产生的电压矢量进行筛选,如图2、图3所示的6个扇区。
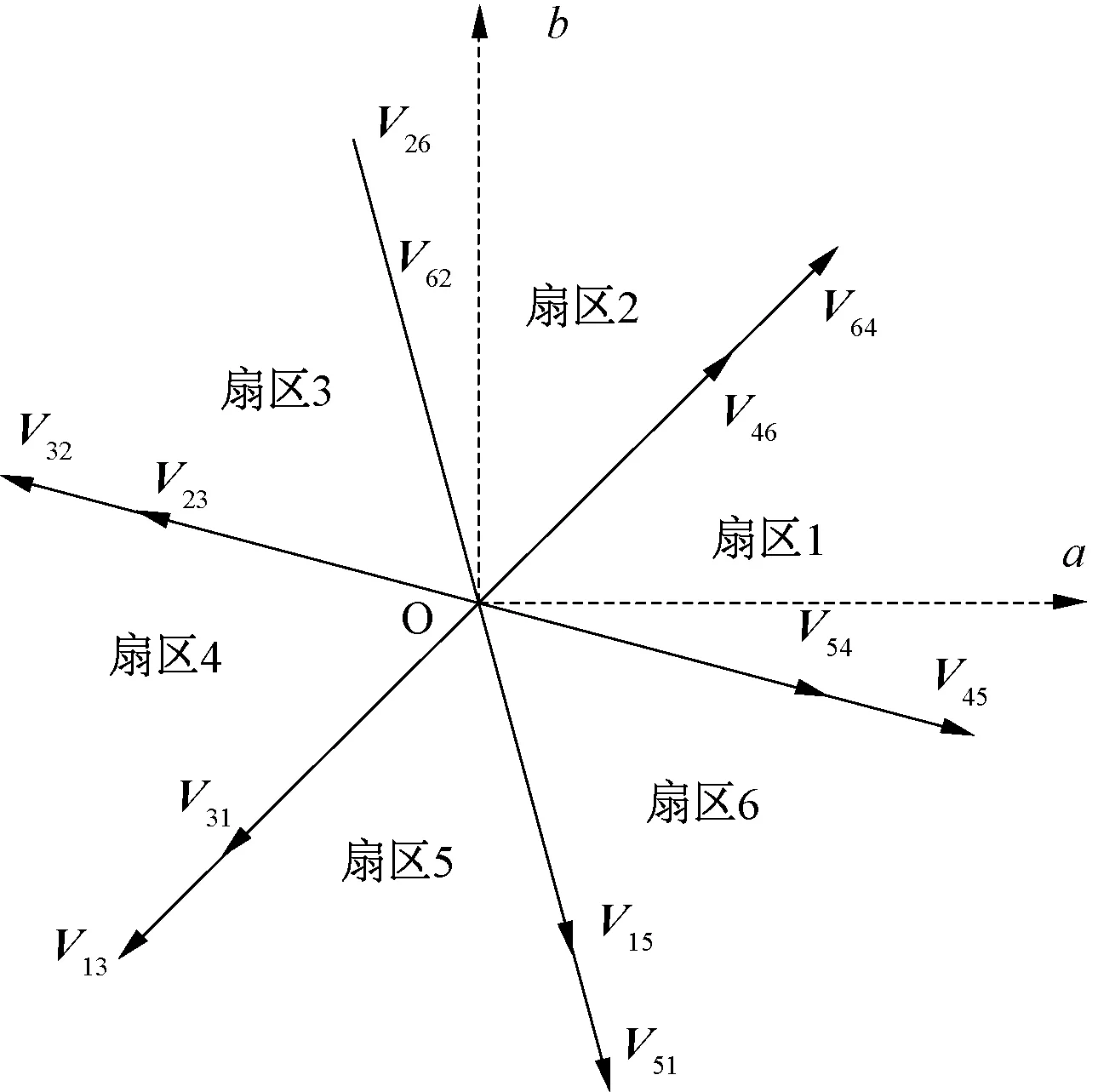
图2 α-β子空间电压矢量图
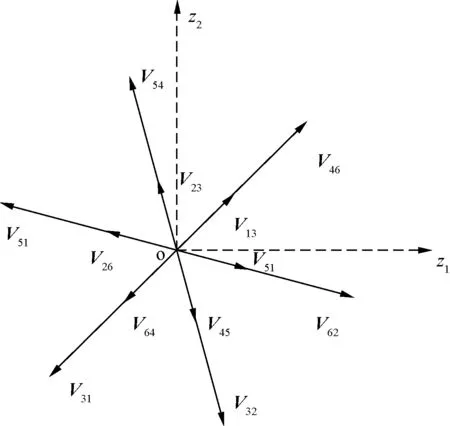
图3 z1-z2子空间电压矢量图
图2、图3中,Vxy中的x和y表示六相开关管导通的十进制数,以每相上管导通设为1,V64表示六相开关管导通状态为110 100。
2.1 矢量作用时间计算
根据平行四边形法则,求得同相位两个矢量作用时间之和:
(8)
(9)
式中:N为扇区号;Vref为参考电压;θ为参考电压矢量在α-β子平面上的角度;|Vmax|为最大参考矢量幅值。
由图2、图3可知,相同相位的两个基本空间电压矢量在x-y空间平面相角相差180°,因此若要控制x-y子空间内合成的电压矢量为零,只要控制两个相位相同的基本电压时间与其幅值成反比即可。
(10)
所以各基本电压矢量作用时间可以按照以下原则进行分配:
(11)
T0=Ts-T1-T2-T3-T4
(12)
式中:T1~T4表示所在扇区4个矢量作用时间;T0表示零矢量作用时间;Ts表示开关周期;|vmax|、|vsec|表示最大矢量和中等矢量的幅值。
考虑到零序电流的存在,可通过调整零矢量V77的作用时间来生成一定的共模电压。利用V77所产生的共模电压去抵消3次谐波反电动势,从而达到抑制零序电流的目的。根据伏秒平衡原则可得:
(13)
将式(13)代入式(8)可得:
(14)
2.2 确定开关时序
以扇区1为例,采用空间矢量脉宽调制方式,可以画出时序波形,如图4、图5所示。
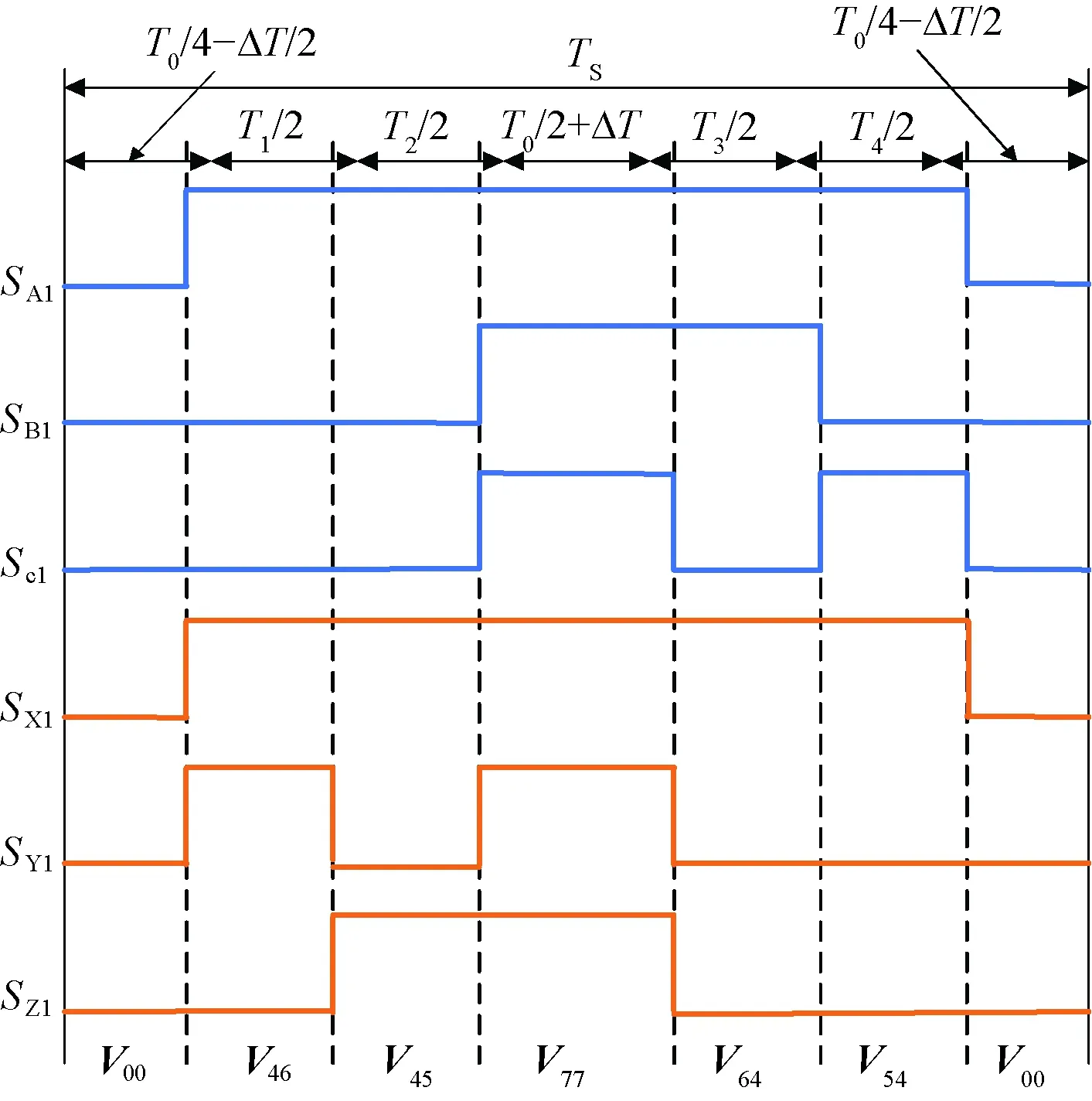
图4 扇区1变流器1开关时序图
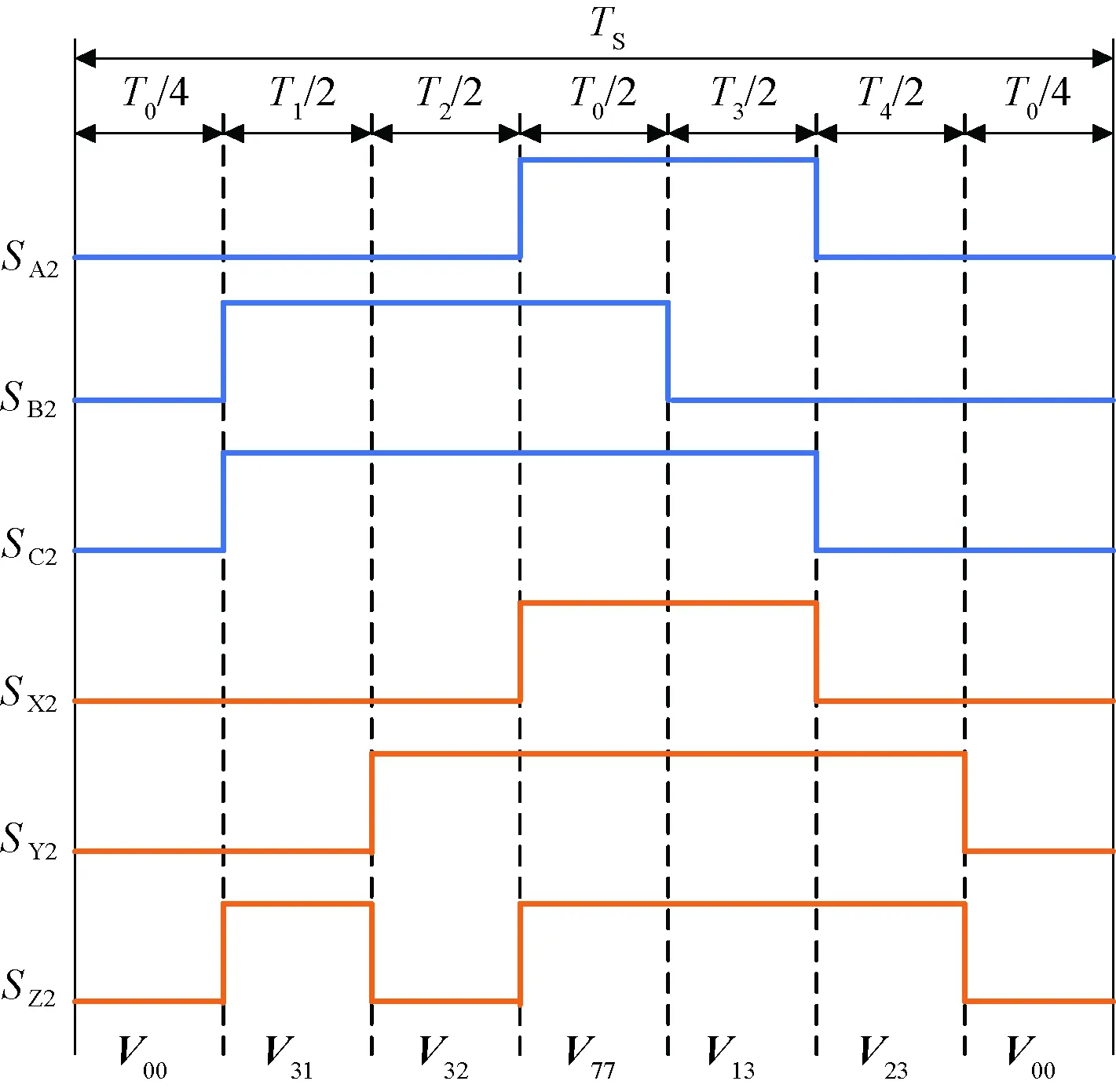
图5 扇区1变流器2开关时序图
图4、图5分别为一扇区变流器1、变流器2开关状态时序图,变流器1在零矢量V77的作用时间相较于变流器2多了ΔT,受零序电流环控制。根据式(13),变流器1和变流器2的共模电压差会和3次谐波反电动势抵消,从而在一定程度上抑制系统的零序电流。
2.3 切换点时间计算
根据图4和图5中的开关时序,可计算开关管的动作时间。定义8个动作时间:
(15)
扇区1变流器1、变流器2的矢量切换点赋值表如表1、表2所示。

表1 扇区1变流器1矢量切换点赋值表

表2 扇区1变流器2矢量切换点赋值表
表1,表2中,Ton表示开关管导通时刻,Toff表示开关管关断时刻。根据切换点时间,可推出期望的PWM信号,以驱动两变流器各开关管。
3 系统控制策略
为了使六相OW-PMSG系统中的零序电流得到有效抑制,引入一个零序电流控制环。结合零序电流中的共模电压和3次谐波反电动势均为交流量,在此选择比例谐振控制器作为零序电流环控制器。将给定值设为0,通过比例谐振控制器输出的指令信号来控制共模电压,从而抵消3次谐波反电动势。零序电流控制环控制方程:
(16)
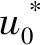
结合零序电流控制环,本文设计的OW-PMSG系统如图6所示。该策略包括4个部分:电压环部分、电流环部分、零序电流环部分以及脉宽调制部分。

图6 OW-PMSG系统控制框图
4 仿真结果与分析
根据上述控制算法,在MATLAB/Simulink中搭建仿真模型,如图7所示。
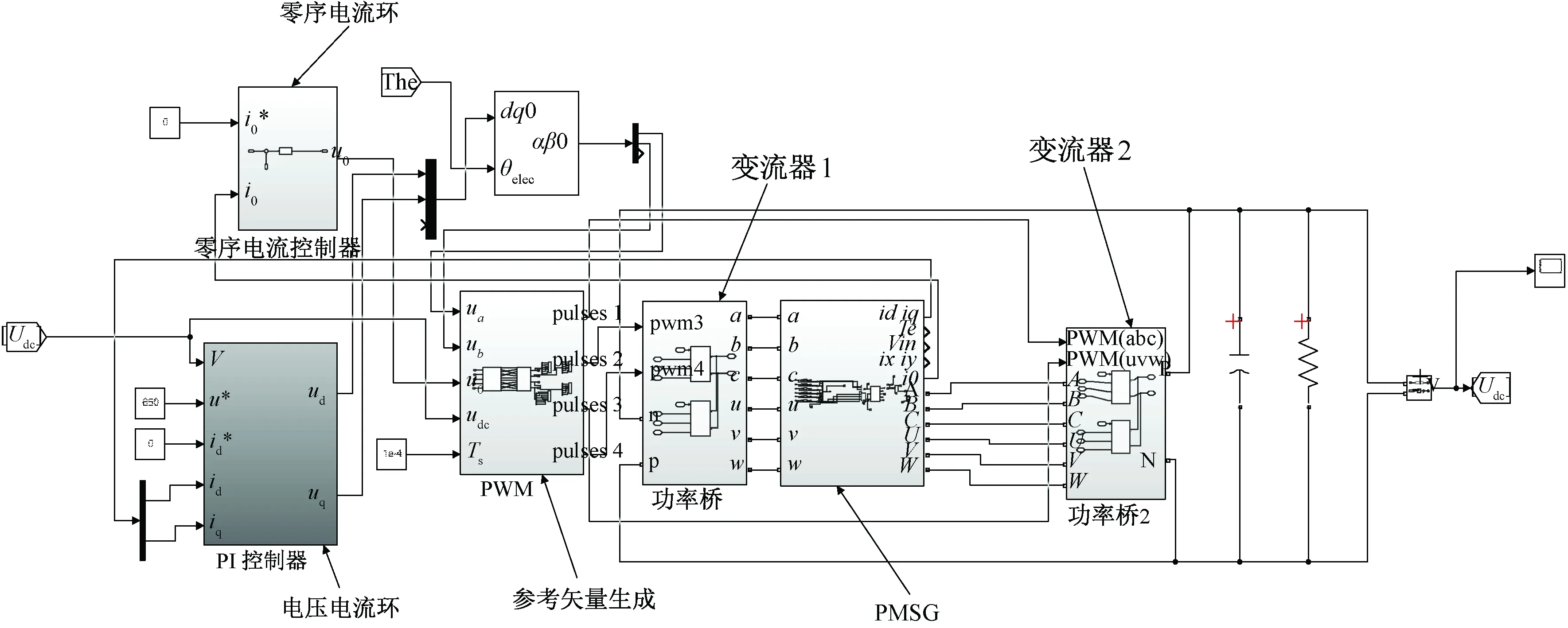
图7 MATLAB/Simulink中基于SVPWM的永磁同步电机系统仿真模型
仿真模型包括六相OW-PMSG、整流桥、电压电流控制环、零序电流控制环等模块。仿真电机为双三相永磁同步电机,其基本电机参数如表3所示。
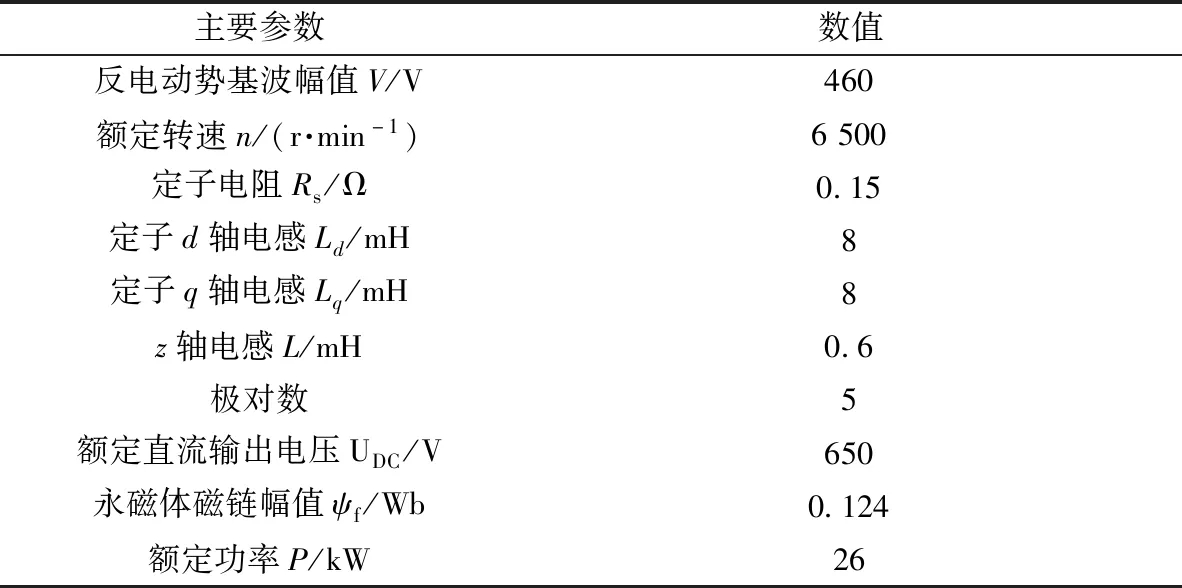
表3 OW-PMSG仿真参数
图8为使用改进零序电流抑制策略前后A相定子电流波形。在传统的四矢量调制策略下,由于零序电流中3次谐波的存在,相电流畸变率较大。在使用了零序电流抑制的调制策略后,相电流畸变小,波形明显趋于正弦。图9为改进前后系统零序电流波形。经过对比发现,在加入了零序电流控制环后,系统的零序电流从1.6 A左右降低到了趋近于1×10-15A,从而验证了零序电流抑制策略的有效性。图10为使用零序电流抑制策略下的直流侧电压波形。

图8 改进前后OW-PMSG A相定子电流

图9 改进前后OW-PMSG零序电流
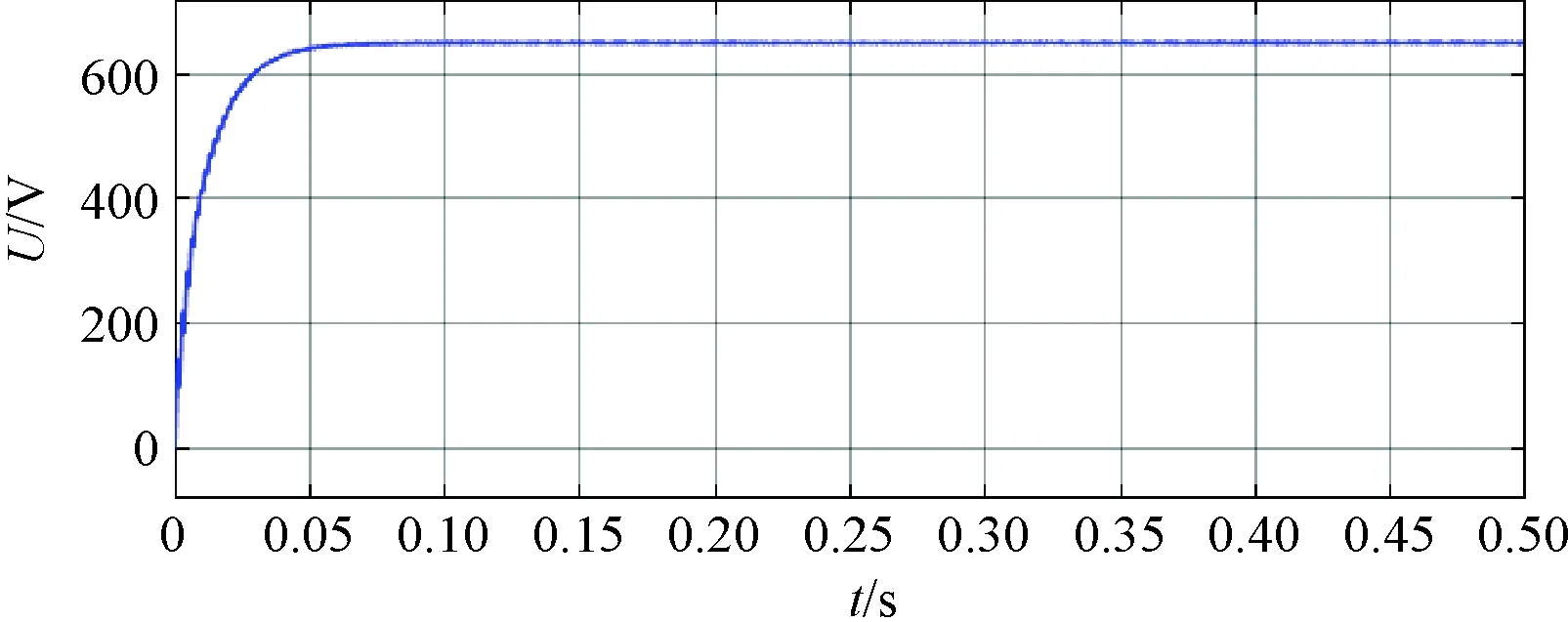
图10 OW-PMSG系统直流侧输出电压
5 结 语
本文在分析六相OW-PMSG零序电流的产生原因和作用方式的基础上,提出一种适用于OW-PMSG的零序电流抑制方法。该方法在保持传统最大四矢量控制对六相电机5次、7次充分谐波抑制的基础上,对零序电流有效抑制,从而避免两者给系统带来的不利影响。仿真结果验证了控制策略的正确性和可行性。