基于梯度下降搜索法的IPMSM最大转矩电流比控制

2022-08-12杨宇健赵世伟杨向宇

微特电机 2022年7期

杨宇健，赵世伟，杨向宇

(华南理工大学电力学院，广州 510640)

0 引言

风机、水泵广泛应用于生产生活的各个领域，其动力源大部分是异步电机，电能利用率较低。相较于传统的异步电机，内置式永磁同步电机(以下简称IPMSM) 具有效率高、结构简单、体积小等优点，在该领域有广泛的应用前景。但现有的控制策略常采用id=0控制，在电机运行过程中往往不能有效利用其磁阻转矩。最大转矩电流比(以下简称MTPA) 控制策略可以合理地分配直轴和交轴电流的值，使得在相同的电枢电流下，产生的电磁转矩最大[1]。MTPA控制对于减小电能损耗、进一步提高恒转矩负载类电机的运行效率有着较大的意义。

目前，对于MTPA的实现策略可以分为离线方法和在线方法[2]。MTPA的离线方法包括查表法、公式法、多项式拟合法等，离线算法需要准确的电机参数和模型，对电机参数的变化较为敏感[3]。在线方法包括搜索法、信号注入法、参数辨识法等。信号注入法通过向电机的定子绕组中注入高频小电流信号实时追踪 MTPA 工作点，但依赖电机参数的准确性[4]。参数辨识法可以在线辨识电机的d,q轴电感参数[5]，但在线计算量较大。在线搜索法可以摆脱对电机参数的依赖，计算量小，具有较高的鲁棒性[6]。搜索法多采用定步长的方式，文献[7]指出，搜索法在负载转矩快速变化时可能会失效，搜索法的的动态性能与稳定性仍有待提高。文献[8]改善了搜索法使能机制，可使搜索法在面对IPMSM的工况变化时具有良好的动态性能。文献[9]分析了定步长搜索法应用于IPMSM调速系统中的稳定性，为调速系统使用该方法提供了理论依据。文献[10]结合了多项式拟合法提出的变步长搜索法，可以加快算法的收敛速度，同时改善动态性能，但其精度依赖于的拟合的函数。文献[11-13]将最优化的理论应用于搜索法，也可加快收敛速度，然而算法的复杂度有所增加。

本文结合恒转矩负载类电机的应用场景，分析了其稳定工作时的恒转矩曲线特性，采用基于梯度下降法的搜索法方案实现MTPA控制。并在传统梯度下降法的基础上，结合电机运行的实际状况对步长加以改进，实现对MTPA工作点的追踪。

1 IPMSM的MTPA控制

对IPMSM而言，其d，q轴的电压方程可以写成：

(1)

式中：Ld，Lq分别为直轴电感和交轴电感；ψf为永磁体磁链；Rs为定子绕组电阻；id，iq为直轴和交轴电流。电磁转矩方程：

(2)

交轴电流iq、直轴电流id和电枢电流is之间的关系：

(3)

式中：θ为电流矢量角。将电磁转矩表达式写成与定子电流和电流矢量角相关的表达式如下：

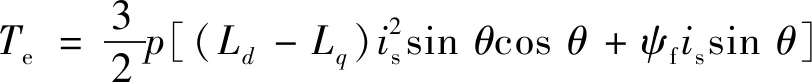
(4)

运动方程：

(5)

式中：TL为负载转矩；J为转动惯量；B为摩擦系数；ωm为电机转速。

式(4)表明，当输出电磁转矩一定时，存在一个最优的电流矢量角θ，使得定子电流is幅值最小。对调速系统而言，采用MTPA控制可以提高电机的运行效率。

从式(4)出发，对电流矢量角求偏导，并忽略电机参数的偏导值，可得：

(6)

2(Ld-Lq)iscos2θ+ψfcosθ-(Ld-Lq)is=0

(7)

对式(7)的一元二次方程求解，可得最优电流矢量角：

(8)

式(8)表明，最优电流矢量角的值由电机的d，q轴电感和永磁体磁链决定，MTPA曲线在d，q电流坐标轴上的轨迹如图1所示。

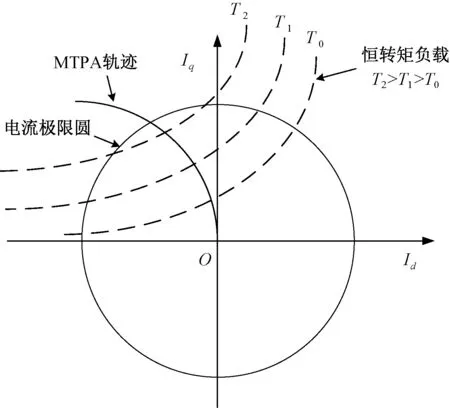
图1 MTPA运行轨迹

在电机实际运行过程中，采用式(8)计算MTPA工作点对电机参数的依赖性较大，而电机参数的测量往往需要较大工作量，不利于MTPA控制的工程应用。

2 梯度下降搜索法工作原理

对于风机、水泵等恒转矩负载的电机，当其工作在稳态时，可以认为输出的电磁转矩Te恒定。此时的MTPA 问题是如何在一定的电磁转矩下，跟踪其定子电流的最小值点。定义目标函数为定子电流is的大小，变量为电流矢量角θ，对于在某恒转矩区工作的电机，MTPA 问题可等效为有约束条件的非线性规划问题：

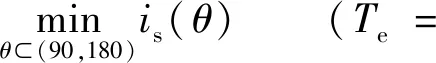
(9)

此时定子电流is和电流矢量角θ满足一定的映射关系，对式(4)求解电流is的解析式可得：

(10)

电流矢量角θ的工作范围为(90°，180°)，可以看出，目标函数is(θ)是以输出电流矢量角θ为自变量的一元非线性函数。电机工作的恒转矩曲线如图2所示，其中定子电流变化量的梯度为▽is=Δis/Δθ。图2中,以MTPA工作点θMTPA为分界线，当电机工作点位于分界线左侧时，其定子电流变化量的梯度▽is<0；当工作点位于分界线右侧时，其定子电流变化量的梯度▽is>0；当电机工作在MTPA工作点附近时，曲线的斜率越来越平缓，达到MTPA工作点时，则有▽is=0。

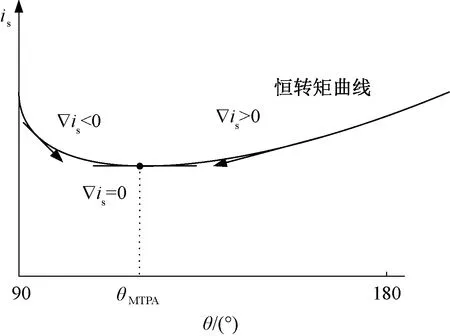
图2 恒转矩区工作下的电机is-θ曲线

综合上述分析的曲线特性，本文拟采用梯度下降法的策略对MTPA工作点进行搜索。梯度下降法的思想是沿着目标函数的梯度方向进行搜索，直至找到目标函数的极值点。采用梯度下降搜索法的收敛过程步骤如下：

(1)选择初始值θ0为初始的电流矢量角，Δθ0为初始步长，置k=0；

(2)以θk+1=θk+Δθk更新电流矢量角，待系统稳定后计算梯度▽is(θk)；

(3)ε为允许的最小误差，如果|▽is(θk)|<ε，则停止迭代，输出θ*=θk+1，否则转到步骤(4)；

(4)以迭代公式Δθk+1=-t▽is(θk)更新搜索步长，t为系统学习率，k=k+1，回到步骤(2)。

上述梯度下降搜索法的迭代收敛过程流程图如图3所示。

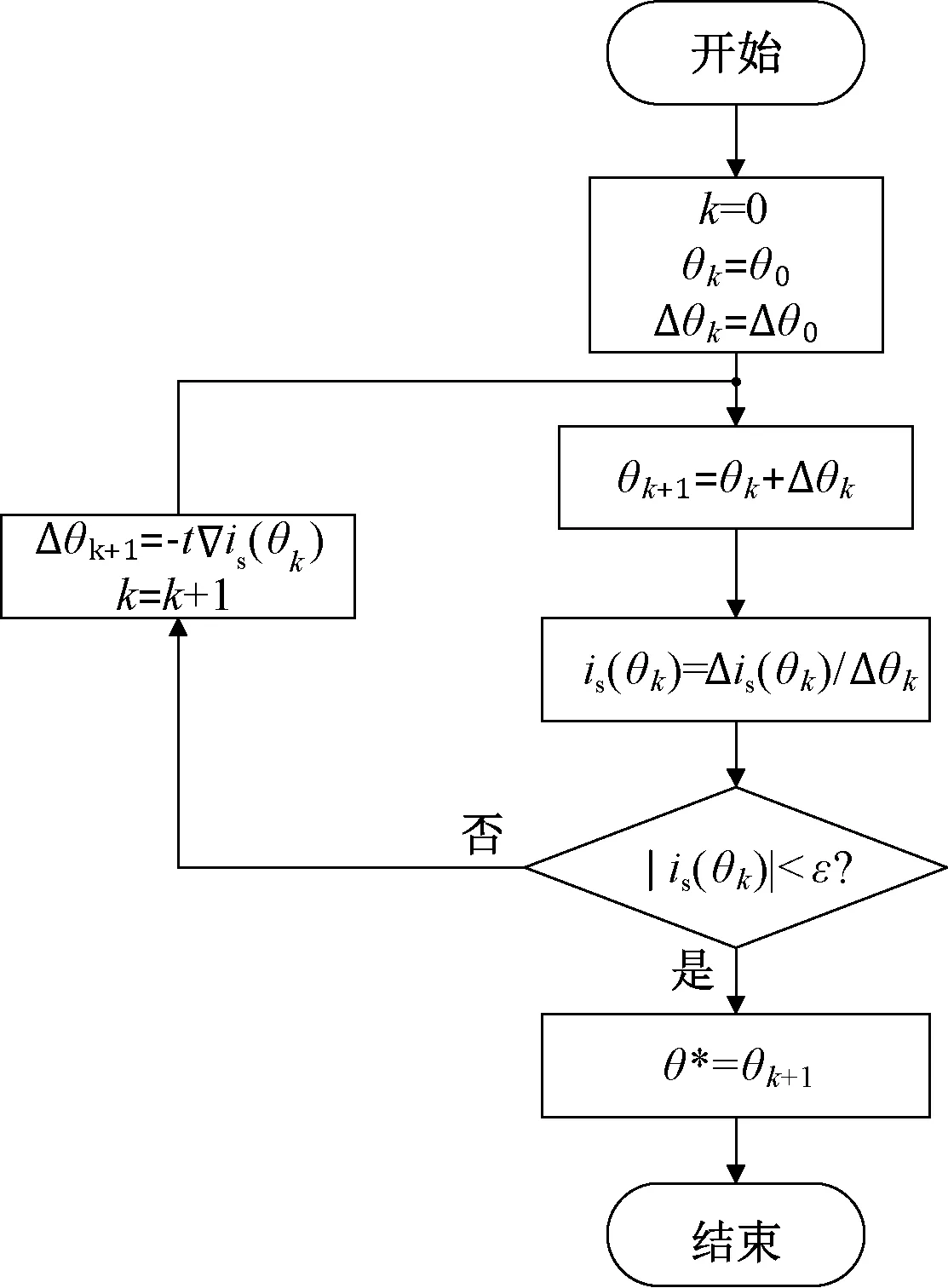
图3 梯度下降搜索法流程图

梯度下降法的步长Δθ是决定算法收敛速度和准确率的关键参数。若步长设置过小，虽能获得良好的准确率，但同时会导致算法收敛速度变慢；而步长设置过大，算法前期会快速运行，但到后期会在极值点附近产生振荡，阻碍算法收敛。针对电机的实际运行状况，本文对传统的梯度下降法步长进行如下改进：

(11)

式中:b为最小步长。在工作点远离MTPA工作点时，采用随机梯度下降法，式(11)中t为常数。当接近MTPA工作点时，由于系统的梯度变化不明显，此时改用定步长的方式进行搜索。

实际应用梯度下降法对工作点进行追踪时，需保证电机的工作点处于一条恒转矩曲线上。因此，应在电机处于稳态工作一段时间后再启用搜索法，并且由于电流环存在一定的调节过程，搜索法的控制周期不能设定得太短，具体时间需结合工程实际设置。

3 仿真结果及分析

为验证上述控制策略的有效性，利用MATLAB/Simulink搭建了系统仿真模型。仿真实验的电机参数如表1所示。

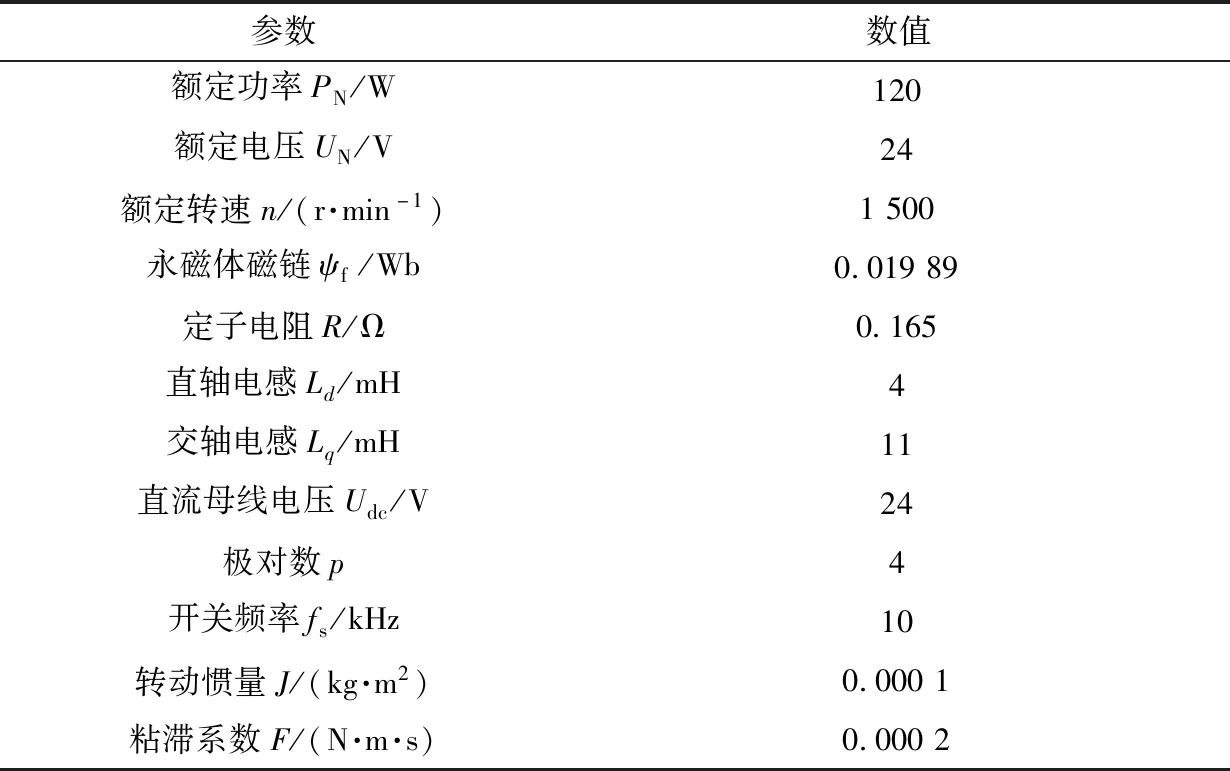
表1 PMSM部分参数

下面仿真验证电机在起动和突加负载后，梯度下降搜索法对MTPA工作点的追踪过程。其中系统的仿真时间为3 s，初始负载转矩为0.1 N·m，在1 s时突加负载为0.2 N·m，参考转速为1 000 r/min。初始电流矢量角为90°，初始步长Δθ0=3°，搜索法控制周期为0.06 s，系数t=125，b=1°，允许的最小误差ε=0.005，仿真实验的波形如图4所示。

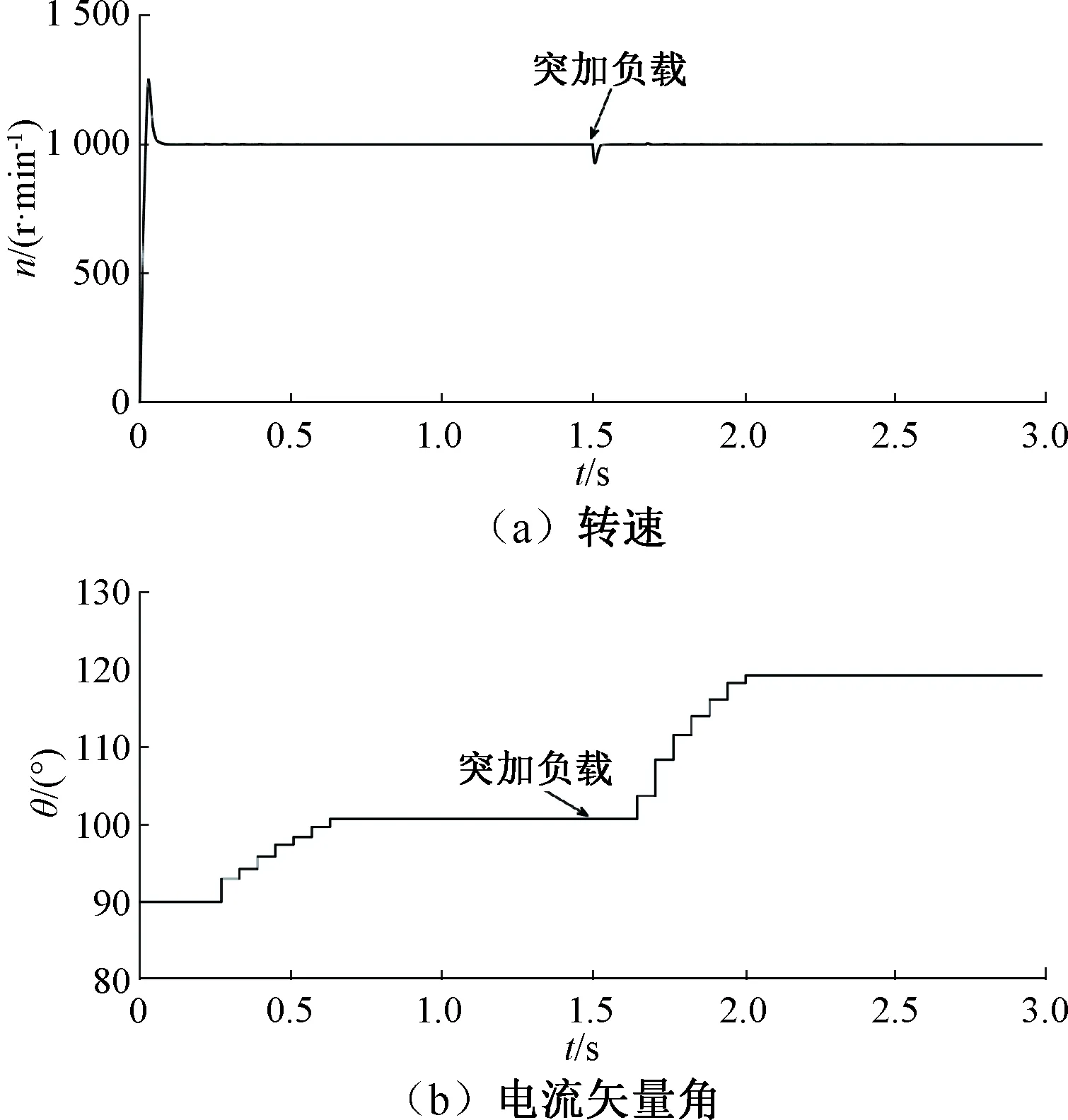
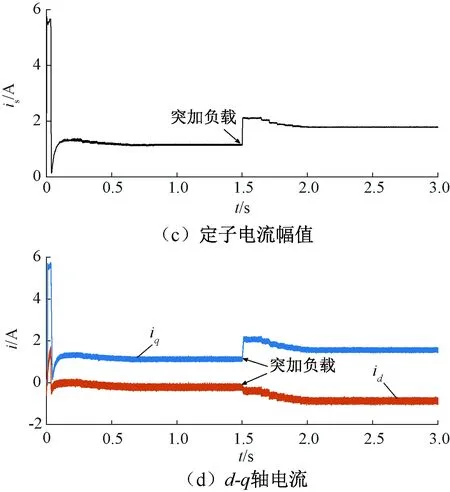
图4 梯度下降搜索法仿真波形

图4(b)显示电机在起动后，于0.27 s时开始搜索MTPA工作点，最终在0.63 s时收敛于100.7°，搜索时间为0.36 s。图4(c)给出了定子电流幅值变化曲线，定子电流幅值从1.32 A减小到了1.14 A，电流幅值下降了约13.7%。

电机在突加负载后，转速出现短暂的下降，其余时间基本维持在1 000 r/min。图4(b)显示，突加负载后在1.64 s时开始搜索MTPA工作点，最终在2 s时收敛于120.2°，搜索时间为0.36 s。观察定子电流变化曲线，在系统突加负载后，梯度下降搜索法实现了MTPA工作点的追踪，电流幅值从2.1 A减小到了1.78 A，电流下降了约15.3%，实现了电机运行效率的优化。

为验证梯度下降搜索法对MTPA工作点的追踪性能，采用传统的定步长搜索法进行对比实验，其中定步长大小为1°，其余的实验条件和梯度法相同，仿真波形如图5所示。

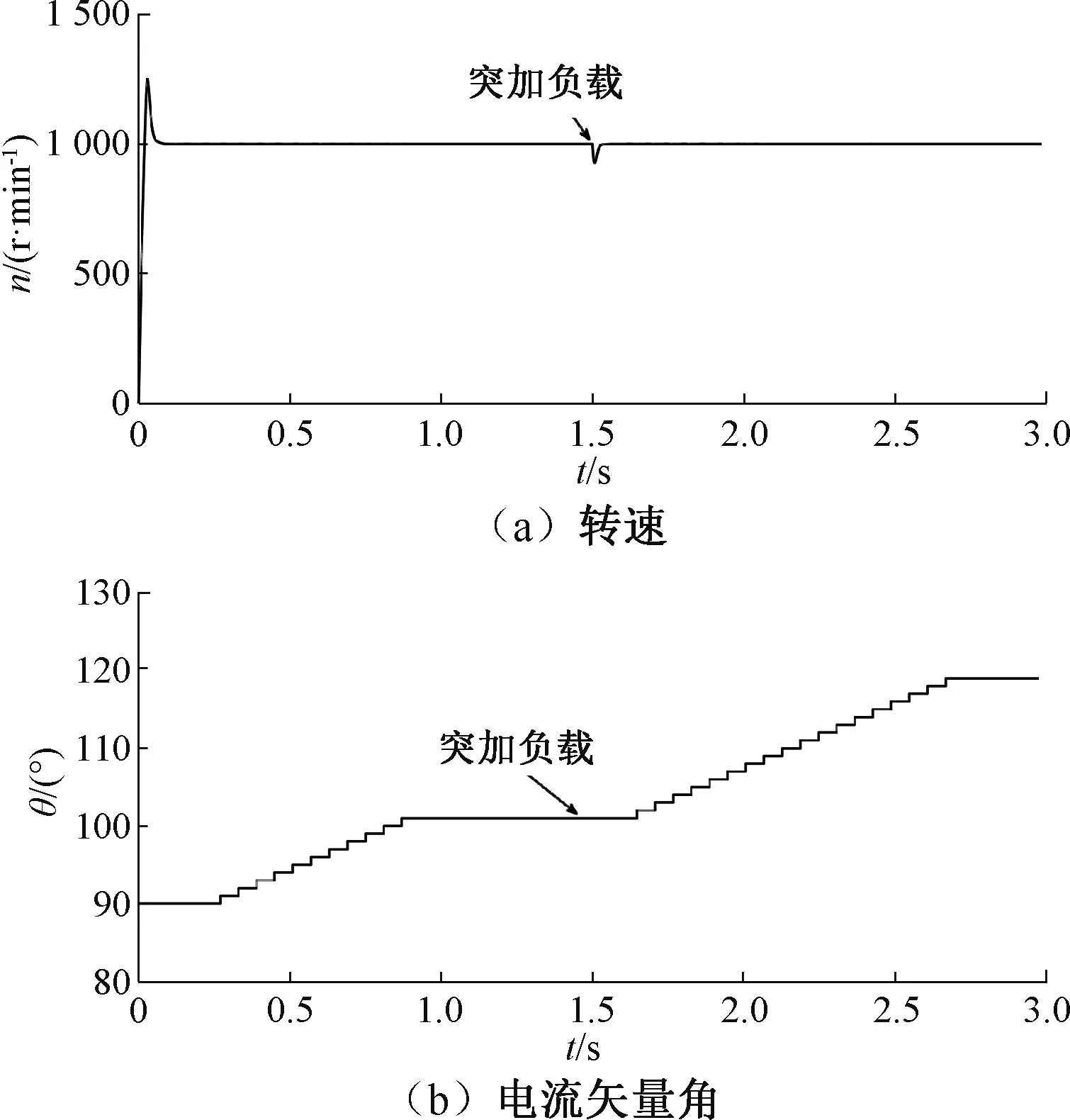
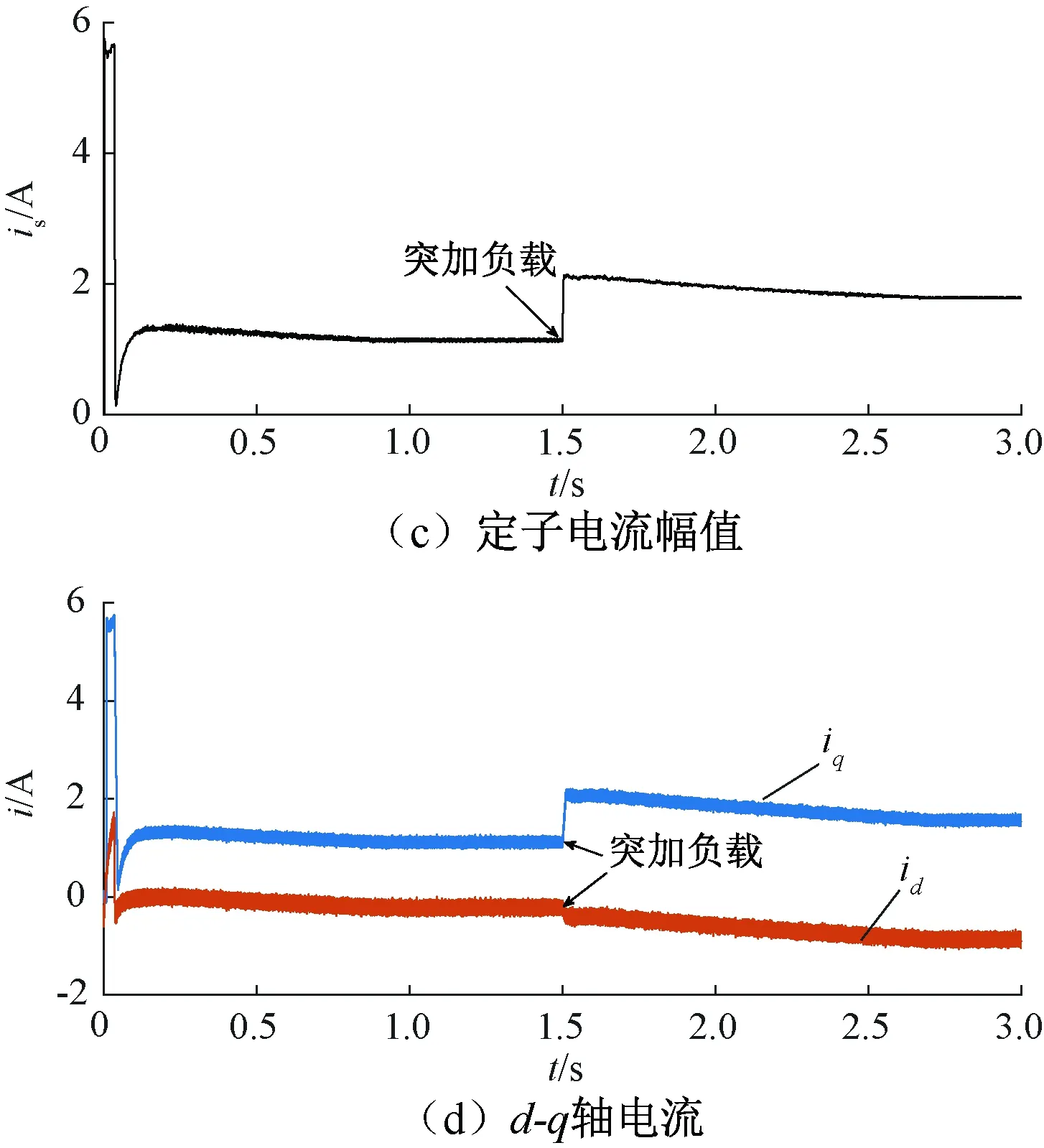
图5 定步长搜索法仿真波形

图5(b)显示，电机起动后，定步长搜索法在0.27 s时开始搜索MTPA工作点，最终在0.87 s时收敛于101°，搜索时间为0.6 s。突加负载后，定步长搜索法在1.64 s时开始搜索MTPA工作点，最终在2.66 s时收敛于119°，搜索时间为1.02 s。

对比图4和图5的仿真结果可知，电机起动后，梯度下降搜索法相较定步长搜索法搜索时间减少了58.6%，突加负载后的搜索时间减少了64.7%，在搜索速度上具有明显优势。两种算法在搜索过程中的电流波形平稳，且转速未出现较大波动，可以认为输出的电磁转矩稳定。对比图4和图5的定子电流幅值和d，q轴电流波形，定步长搜索法的电流变化趋势相对梯度下降搜索法较为缓慢，因此梯度下降搜索法具有更快的响应速度。

4 实验结果及分析

实验平台如图6所示，由直流无刷电机、直流电源、磁粉制动机以及基于STM32微控制器为核心搭建的驱动器组成，实验数据的采集通过串口通信协议传输至上位机平台，如图6所示。实验所用的电机参数和仿真相同。

图6 实验平台

实验验证了电机在参考转速为1 000 r/min，在空载起动以及外界突加负载的情况下，梯度下降搜索法对MTPA工作点的追踪过程。其中，电流矢量角的初始值为90°，初始步长Δθ0=3°。由于电流环存在一定的调节过程，搜索法的周期设定为0.3 s，并且对采集的定子电流做了适当的滤波处理，实验波形如图7所示。

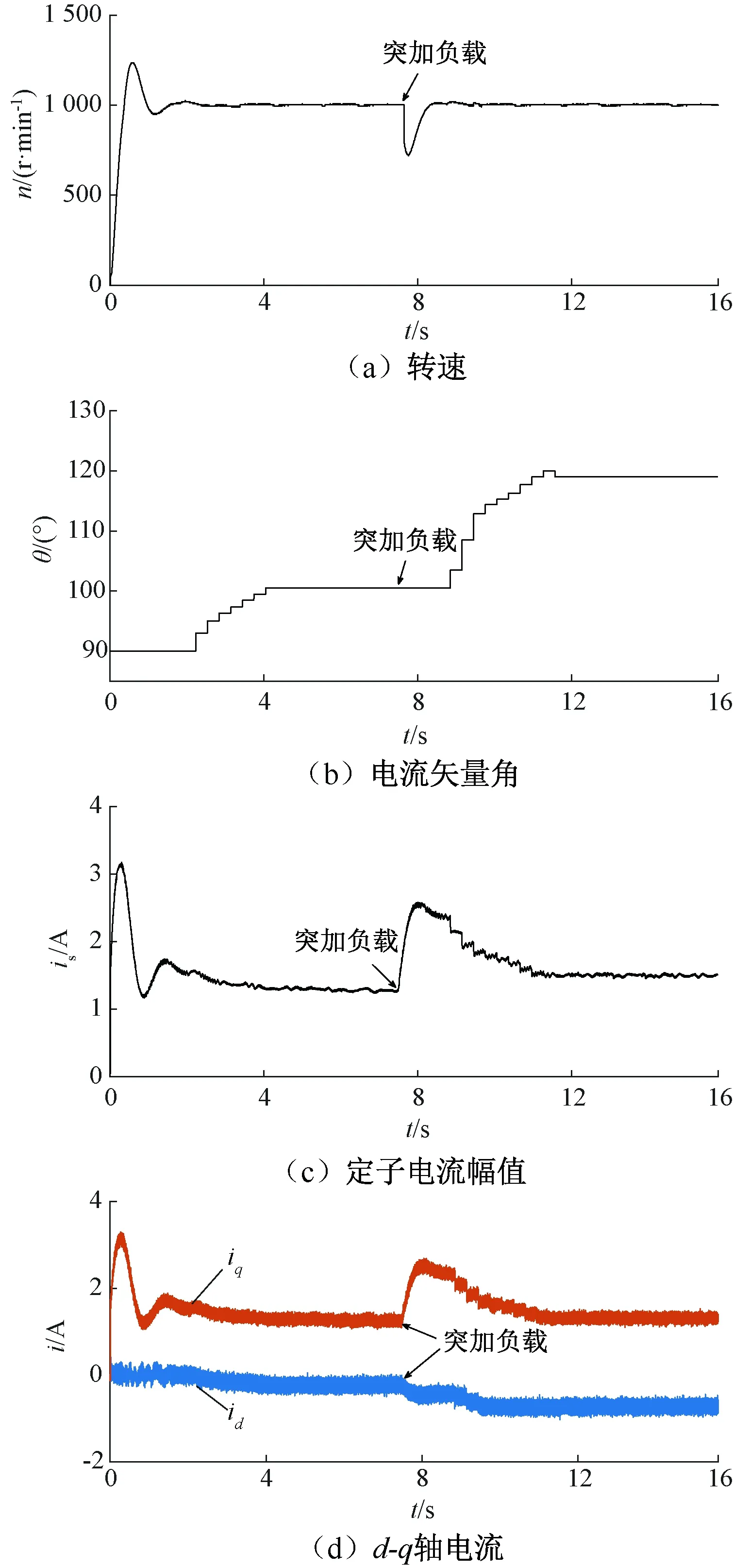
图7 梯度下降搜索法实验波形

观察图7波形可知，电机起动并到达1 000 r/min后，于2 s时开启对MTPA工作点的搜索，并在4.1 s时收敛于100.5°，搜索时间为2.1 s。相比于id=0控制，电流从1.56 A减小到1.28 A，电流下降了约18%。实验于7.6 s时突加负载，电机转速出现短暂波动后重新稳定在1 000 r/min，待电机稳定运行一段时间后于8.6 s时开启对新工况下MTPA工作点的搜索，并在11.6 s时收敛于119°，搜索时间为3 s，定子电流大小从2.13 A减小到1.5 A，电流下降约29.6%。

采用定步长搜索法进行对比实验，其中定步长大小为1°，其余的实验条件和梯度法相同，实验波形如图8所示。

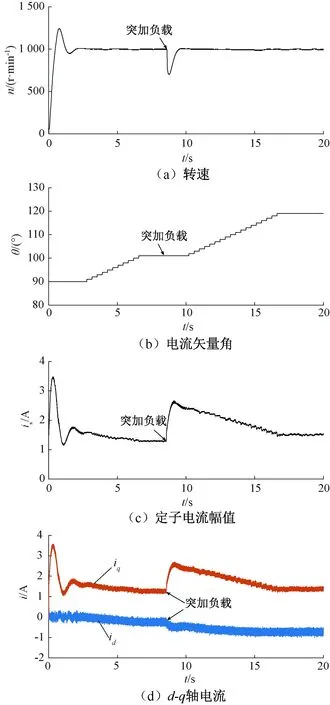
图8 定步长搜索法实验波形

电机起动后，定步长搜索法在2.7 s时开始搜索MTPA工作点，并在6 s时收敛于101°，搜索时间为3.3 s。突加负载后，定步长搜索法在11.1 s时开始搜索MTPA工作点，最终在16.5 s时收敛于119°，搜索时间为5.4 s。

由实验结果可知，梯度下降搜索法在电机起动后的搜索时间比定步长搜索法减少了36.3%，突加负载后的搜索时间减少了44.4%，相较传统搜索算法在收敛速度上提升明显。观察两种算法的实验电流波形可知，在搜索最优电流矢量角的过程中电机转速均未出现较大波动，输出的电磁转矩平稳。对比两种算法的实验电流波形可知，在搜索精度相同的情况下，梯度下降搜索法相对传统算法的电流变化趋势更加明显，响应速度更快。