面向隐私保护的集合交集计算综述

魏立斐 刘纪海 张 蕾 王 勤 贺崇德

(上海海洋大学信息学院 上海 201306)

随着互联网大数据时代的到来，人们通过对大量分布的数据进行挖掘得到其潜在价值，从而更好地服务于人们，如用户爱好推荐系统、广告精准营销等.然而，在挖掘数据潜在价值的过程中，也会产生个人隐私数据泄露等问题，如英国咨询公司剑桥分析公司在未经Facebook用户同意的情况下获取数百万用户的个人数据.因此，实现数据可用不可见，解决数据协同计算和挖掘过程中的数据安全和隐私保护问题就显得迫在眉睫.相关国家和组织也出台保护隐私数据的法令法规，如《中华人民共和国密码法》《中华人民共和国数据安全法》《中华人民共和国个人信息保护法》和欧盟《通用数据保护条例》都强调对数据的治理和隐私保护.数据隐私保护已成为学术界和工业界关注的热点问题.

隐私数据保护最早源于安全多方计算(secure multiparty computation, MPC)，由姚期智[1]借百万富翁问题提出，指各计算参与方无法得到除计算结果外的任何其他信息，解决互不信任的数据持有者如何对隐私数据进行计算的问题.隐私集合交集(private set intersection, PSI)是安全多方计算中的热点问题，允许在分布式场景下各自持有隐私集合的参与方联合计算出集合交集而不泄露除交集以外的任何隐私信息.在隐私保护的场景中，PSI协议具有重要意义，如新冠接触者追踪[2]、隐私通讯录查找[3]、在线广告实际效果计算[4]、基因序列匹配检测[5]等.

传统的PSI协议针对2个参与方设计，Meadows[6]基于公钥加密和利用Diffie-Hellman密钥交换的乘法同态性质提出了第1个PSI协议.随后，由Huberman等人[7]对Meadows[6]的方案做出了完整描述.2004年由Freedman等人[8]借助不经意多项式求值和同态加密构造了第1个安全PSI协议.2017年申立艳等人[9]对安全多方计算框架下的PSI协议进行了简要总结.之后涌现了大量PSI的研究成果，一大批新技术手段和构造框架被提出.除了传统的安全多方计算理论中的混淆电路(garbled circuit, GC)、不经意传输(oblivious transfer, OT)、秘密共享(secret sharing, SS)、同态加密(homomorphic encryption, HE)等技术外，不经意伪随机函数(oblivious pseudo-random function, OPRF)、不经意多项式求值(oblivious polynomial evaluation, OPE)、布隆过滤器(Bloom filter, BF)等集合元素比较技术的应用，使得PSI的效率得到了很大的提高.

现有PSI已经非常高效，但现有很多实际应用中仍然以使用高效但存在安全隐患的解决方案为主，了解现有基于不同密码原语构建的PSI及其特定适用场景，对促进实际场景中使用安全的方案替换存在隐患的方案有很大帮助.在敌手模型方面，研究人员从诚实且好奇的安全模型出发，开始考虑在恶意模型下安全的PSI协议.随着研究人员对隐私集合交集协议的深入研究，除了传统两方PSI协议之外，已衍生出了云辅助PSI、阈值PSI(threshold PSI，TPSI)、不平衡PSI(unbalanced PSI，UPSI)和多方PSI新型应用场景.

本文首先介绍PSI协议的理论基础、敌手模型、安全证明、实现框架，其次系统总结了传统PSI协议的设计框架，随后介绍PSI协议中的集合元素比较技术，进一步详细阐述了适应新型应用场景的PSI方案，最后总结并展望面向隐私保护的集合交集计算中亟待解决问题和发展方向.

1 基础知识

1.1 密码技术

1.1.1 秘密共享

秘密共享技术是许多安全多方计算协议的核心.如何构建秘密分配算法和秘密重构算法是秘密共享方案的重点.Shamir[10]提出的(k,n)秘密共享方案基于多项式插值构建秘密分配算法和秘密重构算法，通过控制多项式的未知系数实现阈值门限.Blakley[11]秘密共享方案基于线性几何投影实现.Jia等人[12]秘密共享方案基于中国剩余定理实现.除了在特定环境下的门限秘密共享方案外，研究者们还设计了安全多方计算环境下的(n,n)秘密共享方案，可直接在比特碎片上进行相应的计算.

1.1.2 同态加密

同态加密允许对密文进行加或乘的操作，满足密文计算后的解密值和明文计算的结果相同.由于整个计算过程是在密文的基础上进行，故同态加密往往被用做外包计算的隐私保护工具.同态加密方案由4个算法组成: KeyGen算法生成公钥和私钥、Encrypt算法加密明文、Decrypt算法解密密文、Evaluate算法计算密文.同态加密根据同态性质可分为加法同态加密(Paillier加密[13])、乘法同态加密(RSA加密[14]、ElGamal加密[15])、全同态加密(FHE[16]).尽管目前全同态加密算法的效率不足以应用于实际场景，但其支持直接密文计算的性质使得同态加密仍受到学术界和工业界的重点关注.

1.1.3 不经意传输

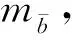
Crépeau[18]提出随机不经意传输协议(random oblivious transfer, ROT)，ROT协议分为离线-在线阶段，离线阶段通过少量OT使得发送方接收随机消息对(r0,r1)，接收方接收随机选择位(b,rb).在线阶段双方只需使用随机消息对对真实输入进行盲化而无需进行昂贵的公钥操作.Beaver[19]提出非黑盒子构造，实现Yao[1]协议中通过少量公钥操作生成大量OT实例.Ishai等人[20]依据矩阵变化思想实现用少量公钥转化为大量OT实例.Kolesnikov等人[21]对OT扩展矩阵进行重复编码实现1-out-of-nOT.2013年Asharov等人[22]提出了2种OT扩展优化和OT相关变体.Boyle等人[23]基于Vector-OLE关联的伪随机发送器和基于LPN假设提出Silent OT扩展(Boyle等人[23]、Schoppmann等人[24]、Weng等人[25]、Yang等人[26])，离线阶段双方执行相关OT生成相关短种子，本地利用PCG将相关短种子无交互的局部扩展为大量相关随机性长源，在线阶段即可利用长源执行多个ROT，大大降低通信复杂度.

1.1.4 混淆电路

混淆电路是一种将任意功能函数转化为电路的通用型基础协议.通过混淆电路表和OT加密电线值实现安全隐私保护.混淆电路的构造思路主要分为3种:1)通过电路混淆者持有2个可能的电线标签，电路评估者持有标签，间接实现电线值秘密共享的Yao[1]协议.2)电路评估者直接持有电线值的秘密份额的GMW[27]协议.3)秘密不再由参与者之间秘密共享而是在电线之间共享，如基于信息安全论构造协议[28].目前混淆电路的研究主要涉及扩展安全模型(如半诚实模型扩展为恶意模型)、减少密文尺寸(如点置换协议[29]、密文混淆协议[30]、免费异或门[31])和降低计算代价.

1.1.5 Hash技术

Hash技术是PSI协议中优化通信复杂度和计算复杂度的重要工具之一，本文列举了最常用的Hash技术构造方法.

1) 朴素Hash(plain Hash).使用hashk(·)将元素映射到具有b个桶的Hash表T中的k个位置，每个桶最多有lb(n)个元素(n为集合的元素个数).hashk(·)表示k个不同的Hash函数h1(·)，h2(·),…,hk(·).

2) 布谷鸟Hash(cuckoo Hash)[32].使用hashk(·)将元素e映射到具有b个桶的Hash表T中的某一个位置，确保每个桶只能有1个元素:计算h1(e)，h2(e)，…，hk(e)，如果T[h1(e)]，T[h2(e)]，…，T[hk(e)]至少有1个桶为空，则随机插入；如果都不为空，则随机选择T[hi(e)]，替换桶中的元素T[hi(e′)]，再对被替换元素e′执行上述操作.当上述替换操作达到一定阈值时，则将e′放置在额外的存储空间stash中.因此，元素e必定在以下容器中找到:T[h1(e)]，T[h2(e)]，…，T[hk(e)]或stash.由于stash可能会存在溢出威胁而导致Hash错误，Pinkas等人[33]通过实验分析出Hash函数个数、stash大小和桶数b的最佳关系.

3) 置换Hash(permutation-based Hash)[34].将元素转化为更短的字符串并存储在Hash表中，以此减少存储空间和计算复杂度.元素插入如下:元素x表示为bit的形式并拆分为2部分x1，x2.为元素获取Hash表的索引:x1⊕H(x2)，H为Hash函数,⊕表示按位异或.最后桶中存储大小为|x2|=|x|-|x1|.|x|表示x的比特长度.

1.2 敌手模型

敌手模型由2个主要方面构成:允许敌手的行为方式和腐败策略.根据敌手是否指示参与方行事可分为半诚实模型、增强半诚实模型、恶意模型.半诚实模型:即使被敌手腐败的参与方也会诚实地执行协议，但在执行过程中会主动收集相关信息，并试图利用这些信息学习协议中的保密信息.增强半诚实模型:在半诚实模型基础上，允许敌手更改起始输入，但在其他输入上诚实地执行协议.恶意模型:允许敌手控制的参与方根据敌手的指示执行协议，偏离原本协议.

根据参与方何时处于敌手的控制可分为静态腐败模型、自适应腐败模型、主动安全模型.静态腐败模型:敌手控制的参与方固定，诚实的参与方从协议开始到结束始终是诚实的，腐败方始终是腐败的.自适应腐败模型:在整个协议执行过程中，敌手可依据需求选择何时腐败和被腐败的参与者.但腐败后的参与者将一直保持腐败模式到协议结束.主动安全模型:参与方只在一段时间内可能被敌手控制，诚实的一方可能会变得腐败，腐败的一方也可能变得诚实.

1.3 安全性证明方法

理想/真实模拟范式[35]是安全多方计算协议最常用的一种证明方法，通过模拟具有安全保证的理想模型与现实PSI协议比较，间接证明其安全性.通过定义理想模型相关的安全目标，避免协议设计过程中安全目标的不完整性.理想模型由完全受信任的三方计算功能函数，并将结果返回给参与方.真实模型通过PSI协议将功能函数拆分为多个消息函数并在参与方之间相互交流完成计算.最后理想模型的视图与真实模型的视图达到不可区分来证明PSI协议的安全性.

1.4 编程框架

借助MPC通用编译器，改善PSI现有技术，减轻设计自定义协议的负担，帮助研究人员快速建立协议实验.本文从支持输入语言、参与方数量、敌手模型和所支持的协议进行简要总结如表1所示，具体详情可参考文献[36].

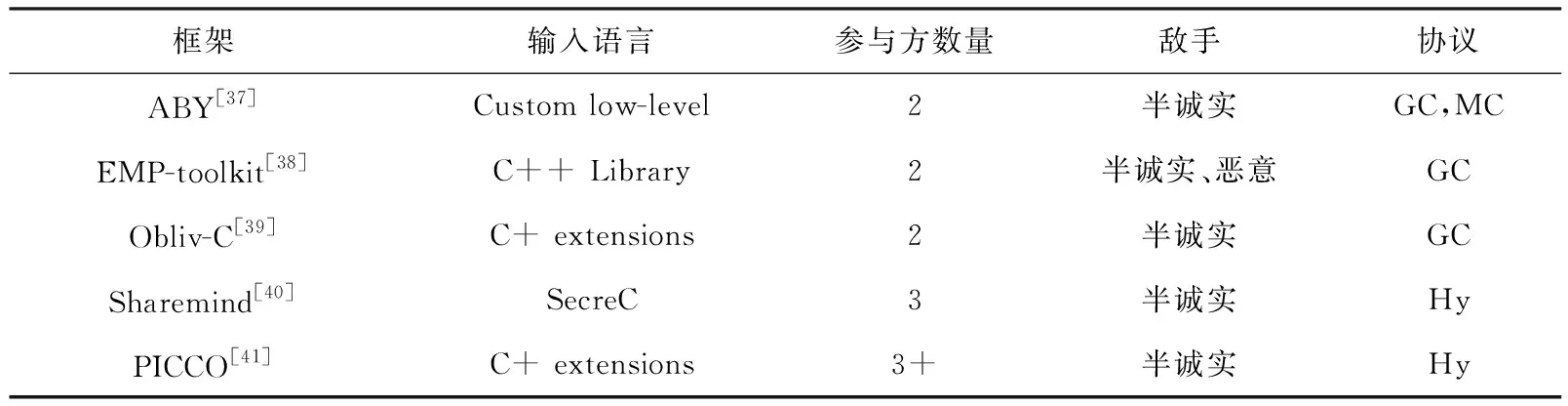
Table 1 MPC Framework Comparison表1 MPC框架对比

2 隐私集合交集的设计框架

2.1 基于公钥加密的设计框架

隐私集合交集协议早期思想直接对元素进行加密，然后在密文上进行相应的比较操作.其最常用的技术是同态加密，发送方加密集合发送给接收方.接收方利用同态加密的性质对密文进行计算，并将计算结果发给发送方，发送方利用私钥对其解密并得到集合交集.基于公钥加密的安全性假设主要分为3类:

1) 基于DH(Diffie-Hellman)假设.Meadows[6]基于离散对数困难问题实现DH密钥交换协议并以此实现PSI功能，Huberman等人[7]发现基于椭圆曲线密码的PSI相较于基于离散对数密码的PSI具有更高的安全性和高效性.

2) 基于RSA假设.De Cristofaro等人[42]基于整数分解困难问题的RSA盲签名技术实现半诚实PSI协议，文献[43]分析基于离散对数密码的PSI协议比基于整数分解密码的PSI协议更加高效.

3) 基于同态加密.Freedman等人[8]将元素表示为多项式的根，利用Paillier同态加密技术加密多项式系数和零知识证明实现两方恶意攻击安全的PSI协议，2016年Freedman等人[44]使用ElGamal加密加快计算效率和布谷鸟Hash技术降低计算复杂度.Kissner等人[45]采用不同的多项式表示方法将计算开销下降到与参与人数呈线性关系.Hazay等人[46]构建一个具有门限解密的加法同态加密方案实现多方半诚实PSI协议.Abadi等人[47]提出基于点-值对的d次多项式表示集合方法，通过Paillier加密方案完成，将乘法复杂度从O(d2)下降到O(d).Jarecki 等人[48]使用加法同态加密和零知识证明来实现伪随机函数(pseudo-random function, PRF).窦家维等人[49]基于有理数编码和三角形面积计算公式并结合Paillier加密实现有理数上的PSI协议.基于公钥加密的PSI协议一般具有较小的通信轮数，适用于具有较强计算能力的模型，但通信带宽和时间复杂度是实际应用中一个很大的瓶颈障碍.

2.2 基于混淆电路的设计框架

混淆电路可将任意函数转化为布尔电路，再进行通用的安全计算.早期基于通用电路的设计方案DPSZ[50]描述了基于算术电路实现集合求交问题:电路生成者通过对称密钥对电路门进行加密，再生成混淆电路并将混淆电路发送给电路评估者；电路评估者对混淆电路对应线路进行解密得到交集，且得不到电路中其他线路的任何信息.其构造的复杂度随电路深度的增加而增加.本文主要讨论专用的电路PSI协议，即在预处理阶段减少电路的比较次数和电路的深度，电路阶段只进行元素的相等性测试以实现通用的PSI协议，并可在电路PSI协议的基础上执行对称函数(交集基数、交集和、阈值-交集).混淆电路有2种抵抗半诚实敌手的电路Yao[1]协议和GMW[27]协议.Huang等人[51]对元素进行特定排序，通过Yao电路合并后进行相邻元素的相等性测试，构造出排序比较乱序电路实现半诚实安全的PSI协议.Pinkas等人[52-54]和Chandran等人[55]基于GMW电路和Hash存储结构进行隐私集合的成员测试构造出OPRF电路实现半诚实安全PSI协议.上述方案通过Hash技术降低比较次数，通过隐私成员测试协议降低电路等值比较的深度，使得电路PSI越来越高效.然而，此类协议需要额外的密钥计算过程和通信，如参与方需要密钥协商等.

2.3 基于不经意传输的设计框架

基于不经意传输技术构造PSI协议通过随机值盲化集合元素产生隐私保护效果.构造思想:首先将集合元素通过特定数据结构存储，然后双方为每一个桶运行OT协议:发送方使用随机值盲化集合元素并将盲化结果发送给接收方，接收方在本地执行相等性测试得到隐私集合交集.由于需要使用大量的OT，传统OT协议限制了PSI协议的安全性和效率性，通过OT扩展技术(oblivious transfer extension, OTE)可有效解决该瓶颈.OTE依据设计思想可分为2类:1)基于矩阵变换的思想利用少量公钥OT实现大量OT实例的IKNP-OT.依据抵御敌手行为能力可分为半诚实安全模型OT协议[20]和恶意安全模型OT协议[56].文献[57]基于布隆过滤器和IKNP03-OT[20]构造出半诚实PSI协议.Pinkas等人[43]将文献[57]中OT协议换为ALSZ13-OT[22]使接收方到发送方的通信量减少一半.文献[58-59]将文献[57]中OT协议换为KSO15-OT[56]并结合Cut-and-Choose技术，以确保Dong协议中的发送方输入不能明显多于其BF中1的数量，实现恶意攻击安全的PSI协议.文献[60]对文献[58]的k-out-of-nOT参数进行改进提供了更好的安全保证.Kolesnikov等人[61-62]、Pinkas等人[63]、Chase等人[64]分别基于1-out-of-nKK13-OT[21]和伪随机函数构造出单点OPRF、不经意可编程伪随机函数(oblivious programmable pseudorandom function, OPPRF)、多点OPRF(multi-point OPRF, mOPRF)、带权多点OPRF实现具有半诚实安全的PSI协议.Pinkas等人[65]基于OOS17-OT协议[66]构造具有恶意安全的PSI协议.2)基于子向量不经意线性评估实现具有更低的通信效率但计算复杂度增加的Silent-OT.Rindal等人[67]基于半诚实安全的Schoppmann等人[24]协议和恶意安全的Weng等人[25]协议分别构造出半诚实安全和恶意安全的PSI协议.基于OT的PSI协议一般具有较低通信和计算量，本文依据设计思想、功能和安全模型对现有PSI协议进行分类如表2所示：

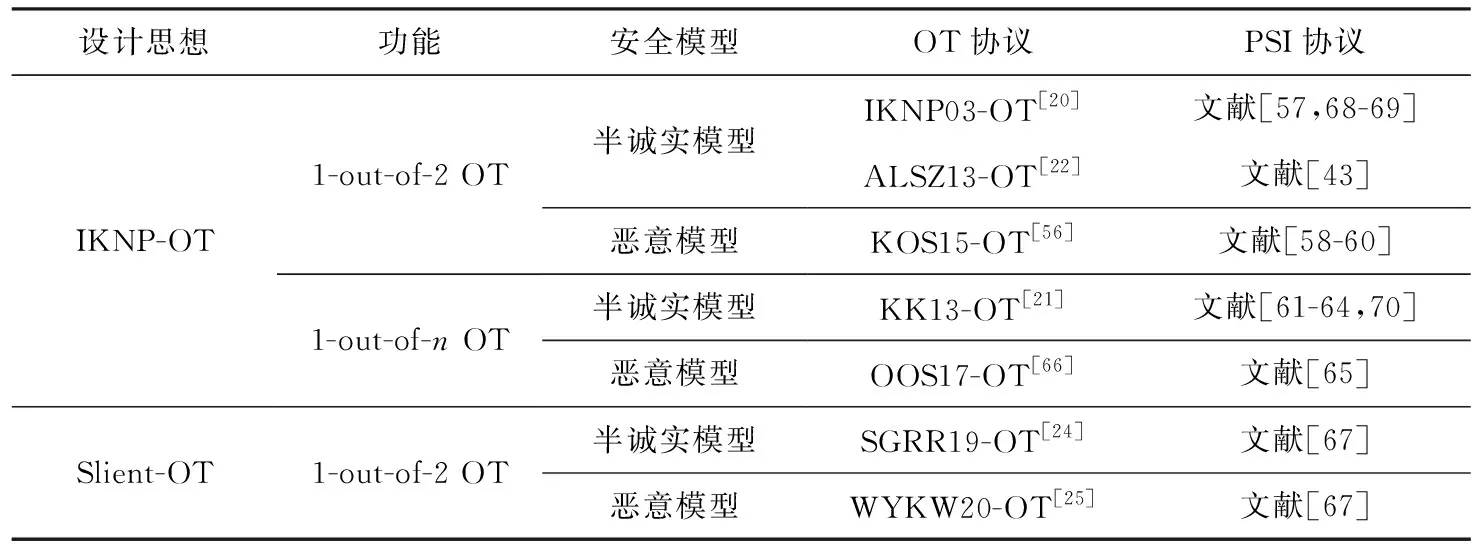
Table 2 PSI Protocols Based on OT Framework表2 基于OT框架的PSI协议

3 隐私集合元素比较技术/工具

3.1 不经意伪随机函数

利用OPRF设计PSI协议是一种常见的思想.OPRF允许接收方输入x，发送方输入密钥k，接收方输出Fk(x)，发送方无任何输出.然后发送方本地计算Fk(y)并将其发送给接收方.接收方通过比较Fk(x)和Fk(y)可以构造出PSI.基于OPRF构造PSI的论文进展如图1所示：

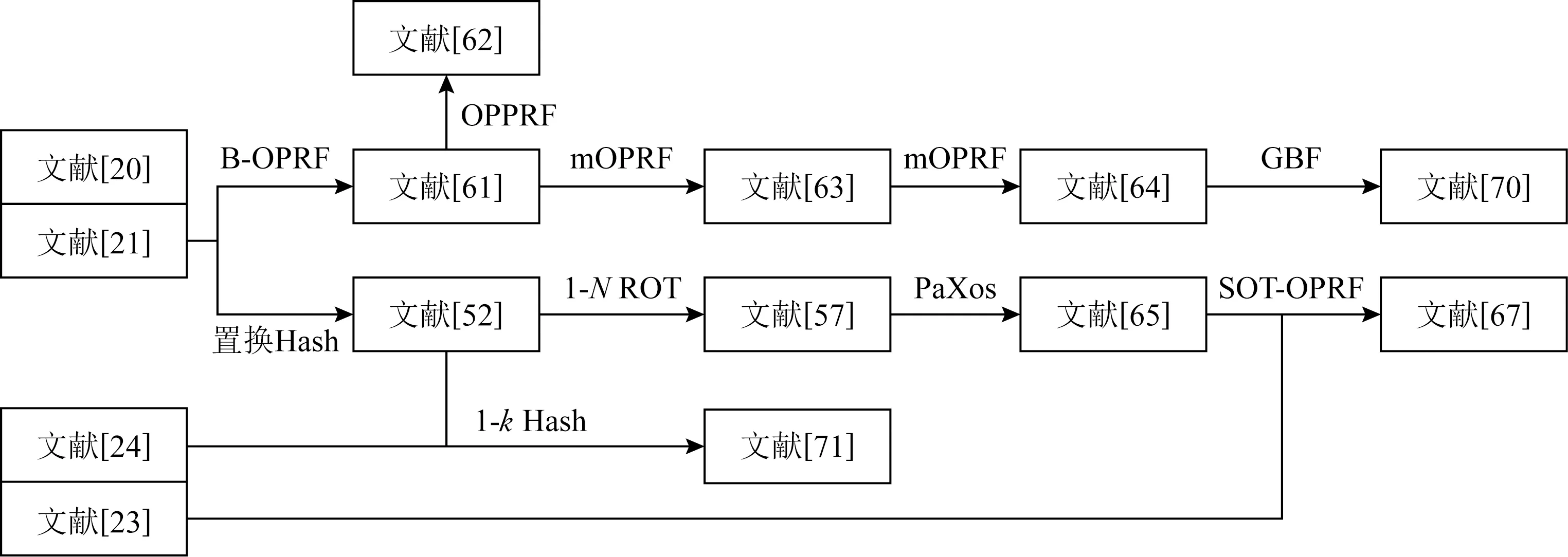
Fig. 1 The progress of OPRF based PSI protocols图1 基于OPRF的PSI论文进展

Naor等人[72]基于Diffie-Hellman假设和标准1-out-of-2 OT构造出第1个OPRF，Hazay等人[73]利用上述OPRF实现安全的PSI协议，满足单边恶意敌手模型，但其使用的是非单向映射的PRF，可能会因恶意选择PRF密钥而产生冲突.Jarecki等人[48]基于Dodis-Yampolskiy[74]提出的具有O(1)指数幂的单射伪随机函数:fk(x)=g1/(k+x)和Paillier同态加密完成OPRF构建.协议需要多个模N2的指数运算，导致计算量非常大.Debnath等人[75]通过零知识证明技术和引入半可信第三方，构造出双方获取交集结果的OPRF.Jarecki等人[76]基于不可预测函数:fk(x)=(H(x)k)和Hash函数完成OPRF:fk(x)=H′(H(x),H(x)k)构建.构造PSI协议:P2使用随机值a盲化H(x)得到y=H(x)a并将其发送给P1.P1使用密钥k加密y得到z=yk并将其发送给P2.P2即可得到fk(x)=z/a=H(x)k.通过外层Hash函数和对密钥k进行零知识证明以抵抗恶意敌手的攻击.

Kolesnikov等人[61]基于随机OT[20]协议改进了1-out-of-2 OT扩展并结合对称密钥和位运算构造出单点OPRF:fk(x)=H(q⊕[C(x)∧s])(其中密钥k由q,s∈{0,1}n组成，∧表示按比特位与操作):双方首先通过布谷鸟hashk将集合映射到布谷鸟Hash表中，以降低比较次数.再对每一个桶执行单点OPRF操作，P2随机均匀采样字符串r0={0,1}n计算r1=r0⊕C(y)，P1随机采样字符串s={0,1}n.双方分别输入r1和s执行n轮OT，最后P1接收n位{rs[j][i]}i∈n,s[j]∈{0,1}.P1计算q=rs[1][1]‖rs[2][2]‖…‖rs[n][n]得到OPRF密钥k=(q,s).P2输入y到OPRF输出值H(r0).如果x=y，则q⊕[C(x)∧s]=r0，即得到交集.

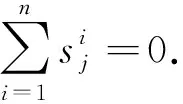
由于文献[61]中每个元素被多个Hash函数映射，从而导致每个元素都需执行多个单点OPRF操作.Pinkas等人[63]通过多项式插值技术结合IKNP-OT设计了1个稀疏OT扩展，其允许接收方从n个随机秘密中不经意地选取k个以此实现多点OPRF(multi-point OPRF, mOPRF)，即实现每一个元素只需要1个OPRF操作.该协议通过选择与稀疏OT吻合的Hash结构:2-选择Hash[77]，不需要伪随机填充值，且每个桶可放入多个元素，使得比较次数下降.但是与文献[61]相比，mOPRF需要在1个大的域上计算和插值1个高阶多项式从而产生较高的计算开销，比文献[61]仅使用对称密码和位运算要花费更多的成本.Chase等人[64]仅利用OT、Hash函数、对称密码和位运算构建mOPRF，相比于文献[63]基于多项式插值的OPRF更有效率，通过分析文献[61]的协议构造可知无论发送方选择不同s所得到的密钥k，都有fk(y)=H(r0)，基于这一发现构建了1个新的mOPRF:新的OPRF密钥包含一个大小为m×w的矩阵M.发送方选择随机字符串s∈{0,1}w，接收方准备2组列向量A1,A2,…,Aw∈{0,1}m，B1,B2,…,Bw∈{0,1}m.两方执行w个OT,发送方作为接收者得到w个列向量，由此得到OPRF密钥M.接收方输入元素y得到fM(y).发送方计算自身集合的fM(·)发送给接收方即可实现PSI协议.

Kavousi等人[70]采用星型-路径(star-path)网络结构并结合文献[64]的mOPRF构造出半诚实多方PSI协议.star模块用于指定方Pt作为发送方与其他所有参与者执行OT，使得Pj(j∈[1,t-1])秘密共享Pt的矩阵并得到1个随机字符串的列向量矩阵.path模块用于重构秘密，即每一个参与方仅向最后参与方的方向的相邻参与方发送混淆布隆过滤器(garbled Bloom filter, GBF)，一直持续到Pt-1，Pt-1计算GBF和OPRF值，并将OPRF值发送给指定方Pt，Pt通过比较OPRF值得到交集.这种设计使得每一方(指定方除外)的通信和计算复杂度仅取决于其自己的输入集大小，而不取决于协议中涉及的参与方数.

Hemenway等人[71]提出基于1-out-of-kHash和Silent-OT[23]构建OPRF实例.Silent-OT相较于IKNP-OT具有通信量显著下降的特点.使用Silent-OT协议和1-out-of-kHash实现离线预处理阶段计算其元素的最优分配.1-out-of-kHash通过数组A表示集合S，对于hashk查找x只需检查是否A[hi(x)]=x，其具有高效的空间利用率和恒定的查找时间.当双方不需要动态插入元素时，多项选择Hash比布谷鸟Hash具有更好的性能，即可以在本地计算最优分配.

Pinkas等人[65]通过改进布谷鸟Hash算法(probe-and-XOR, PaXoS)并结合OOS-OT[66]实现了第1个基于布谷鸟Hash的恶意安全PSI协议.PaXoS是1个将n个二进制字符串映射到m个二进制字符串的随机函数，由Hash映射到对应插槽值异或得到集合元素，以消除布谷鸟Hash构建恶意PSI时泄露发送方未在集合交集中的集合信息问题.同时PaXoS具有与GBF相同的渐进编码和解码，但计算速率却比GBF快.该文主要通过OOS协议的同态性质构建PSI协议.

Rindal 等人[67]基于Vector-OLE[24]和PaXoS[65]数据结构提出批量化的OPPRF(batch-OPPRF,B-OPPRF)新构造.基于Vector-OLE[24]的Silent-OT构造新的OPRF，具有O(n)的通信量和计算量非常高效，并且以很小的开销可实现恶意安全性.基于PaXoS数据结构实现了新型可编程PRF，PaXoS具有编解码高效，其只需O(1)时间复杂度计算.

3.2 不经意多项式评估

Freedman等人[8]将元素比较问题转化为多项式求根问题，通过乘法同态加密性质实现PSI.参与方P1和P2分别拥有集合X1和X2.首先P2利用具有乘法同态属性的方案生成密钥对(PK,SK)，将集合X2的元素作为多项式的根构建|X2|阶多项式Q(·)，加密多项式系数发送给P1.P1对集合X1中的元素打乱并选择1个随机值rj，利用同态加密方案计算rj×Q(xj)+xj并将其发送给P2.P2解密，如果z属于X1∩X2，则对任意的r都有r×Q(z)+z=r×0+z=z.否则r.Q(z)+z是1个随机值.如果多项式的阶数较大，将导致同态加密的指数计算成本较高.

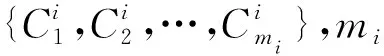
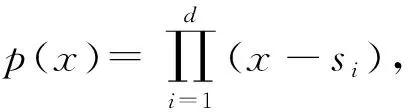
3.3 混淆电路

混淆电路可将任意函数转化为布尔电路，故集合求交也可由电路构造.基于电路的PSI协议通常效率低下，但仍是研究的热点，因其具有通用性，不必更改主电路只需添加子电路，即可实现基于求交的函数，比如交集基数等.基于电路的隐私集合求交最朴素的想法是利用与门对大小为n的2个集合进行n2次比较，但其完全由电路构造产生了很高的通信复杂度.电路计算的通信量由比较次数、元素大小以及电路安全参数决定.然而元素大小和电路安全参数都是给定的，所以设计计算交集的电路困难之处在于决定哪些元素需要进行比较.基于混淆电路构造PSI的论文进展如图2所示：

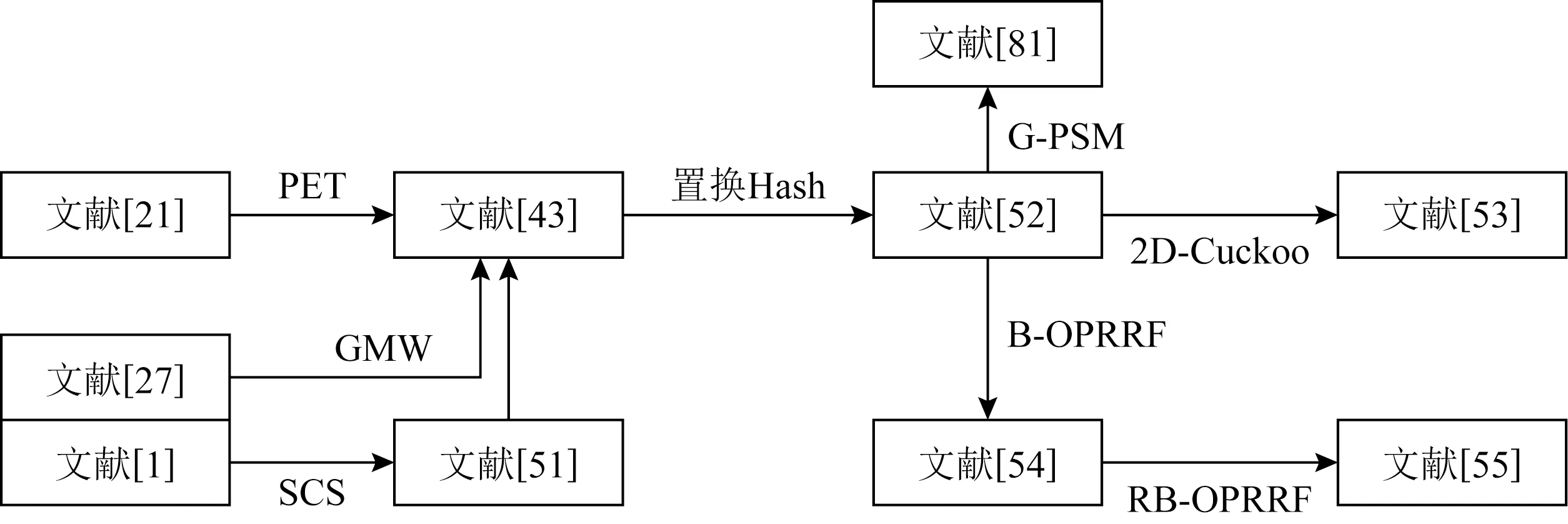
Fig. 2 The progress of GC based PSI protocols图2 基于GC的PSI协议进展

Huang等人[51]提出了3种基于混淆电路的相等性测试(private equality test, PET)以实现隐私求交功能.第1种位与协议:将集合通过二进制向量表示，然后通过与门进行逐位与操作即可完成相等性测试.第2种是元素直接比较.第3种排序比较乱序协议(sort compare shuffle, SCS)，双方以特定方式本地排序集合输入，通过不经意合并排序网络计算2个集合的并集排序列表.然后通过混淆电路进行相邻元素比较得到集合匹配列表，其比较次数为O(nlogn).最后通过乱序网络对其进行重新排序以保证匹配元素位置信息不被泄露.

Pinkas等人[43]使用GMW协议优化了SCS电路协议，通过减少OT次数对协议的通信进行优化.随后他们[52]提出电路阶段化的思想:通过置换Hash技术减少元素的存储大小和降低比较次数，再应用电路进行隐私成员测试(private set membership, PSM)评估.具体协议为:参与方P0使用布谷Hash算法构建布谷Hash表T0，P1构造朴素Hash表T1.由Hash性质可知，P0和P1集合中的相同元素一定在2个Hash表的同一行.再通过电路逐行进行隐私成员测试，由于各方须隐藏映射到桶中的元素个数，因此剩余位置需填充虚拟值，由此产生不必要的比较.该协议将比较次数从O(n2)下降到O(nlogn/log logn)(n为集合大小，logn由布谷Hash表性质决定)且使电路的深度不再和集合大小相关.

Pinkas 等人[53]设计了一种2维布谷鸟Hash，将比较次数下降到O(n)使得布尔电路计算交集的开销只需ω(n).2维布谷鸟Hash结构由2个表TL，TR和4个公共Hash函数HL0，HL1，HR0，HR1组成.P2使用布谷Hash算法插入到表TR中.P1通过HL0，HL1将元素插入TL，或通过HR0，HR1将元素插入TR，通过改进的布谷鸟插入算法实现.即P2将其每个元素映射到每个表中的1个子表.P1将其每个元素映射到其中1个表的2个子表.确保P1和P2的交集元素被映射到同一个子表中.最后共同构建1个电路，对每个桶中双方存储的元素进行比较得到交集.

Ciampi等人[81]基于文献[52]的阶段化思想，进一步设计了一个结果秘密共享的PSM协议，最后电路只需要做相等性测试，以此减少电路尺寸.该协议基于不经意图跟踪构建隐私成员测试协议为:发送方构造1个二叉树，每个节点包含1个对称密钥.发送方输入二叉树，接收方输入测试元素，双方执行1-out-of-2 OT.其允许接收方不经意地遍历树，将成员测试结果秘密共享，最后通过电路等值比较得到交集.

Pinkas等人[54]设计了1个B-OPPRF协议以完成隐私成员测试，将结果输入电路执行相等性测试.通过布谷鸟Hash和朴素Hash将隐私集合求交问题简化为h个隐私成员测试问题.当调用b个OPPRF实例时，桶中隐私元素个数不一致导致每个桶的编码数量不同，但是其总的编码数量是固定的，故设计了1个提供大小为N并进一步隐藏每个桶中编码点数量的原语称为B-OPPRF.通过B-OPPRF协议完成隐私成员测试:P1作为发送者，在1个包含b个OPPRF独立实例的B-OPPRF实例中，在第j个OPPRF实例中将所有编程输出设置为单个随机值tj.然后P0评估第j个OPPRF的T0[j]，如果T0[j]=T1[j]则P0和P1持有相等值.最后通过电路比较Fk(x)，因此该电路只需要对每个桶进行1次比较计算.通过B-OPPRF将桶的比较次数从O(logn)减少到1，但OPPRF在创建提示时使用多项式插值，导致计算复杂度增加.Chandran等人[55]基于上述B-OPPRF设计了1个严格的RB-OPPRF.通过使用1个具有3个Hash函数的布谷鸟Hash结构取代多项式插值结构完成B-OPPRF操作，将每个桶的比较次数从O(logn)减少到3，同时只产生线性计算开销.

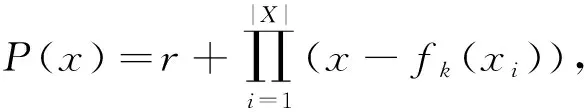
3.4 布隆过滤器

布隆过滤器[84]是一种对集合进行编码的数据结构，其利用若干独立分布的Hash函数将集合中的每个元素映射到二进制数组中最终得到1个轻量级1维数组，是有效进行集合相等性测试的工具.未保护隐私的BF构造PSI思想为:参与方P1和P2分别拥有集合S1和S2，参与方P1依据hashk构造1维数组bf1，将bf1的所有位设置为0，对每个x∈S1，计算hashk(x)作为bf1的索引并将对应位设置为1.P2为元素y进行相等性测试，即hashk(y)对应的bf1均为1，则y属于S1.BF存在一定的错误率，其与Hash个数、BF长度、集合大小有关.文献[85]对其进行详细的分析并给出最佳BF构造参数.基于布隆过滤器构造PSI协议进展如图3所示.

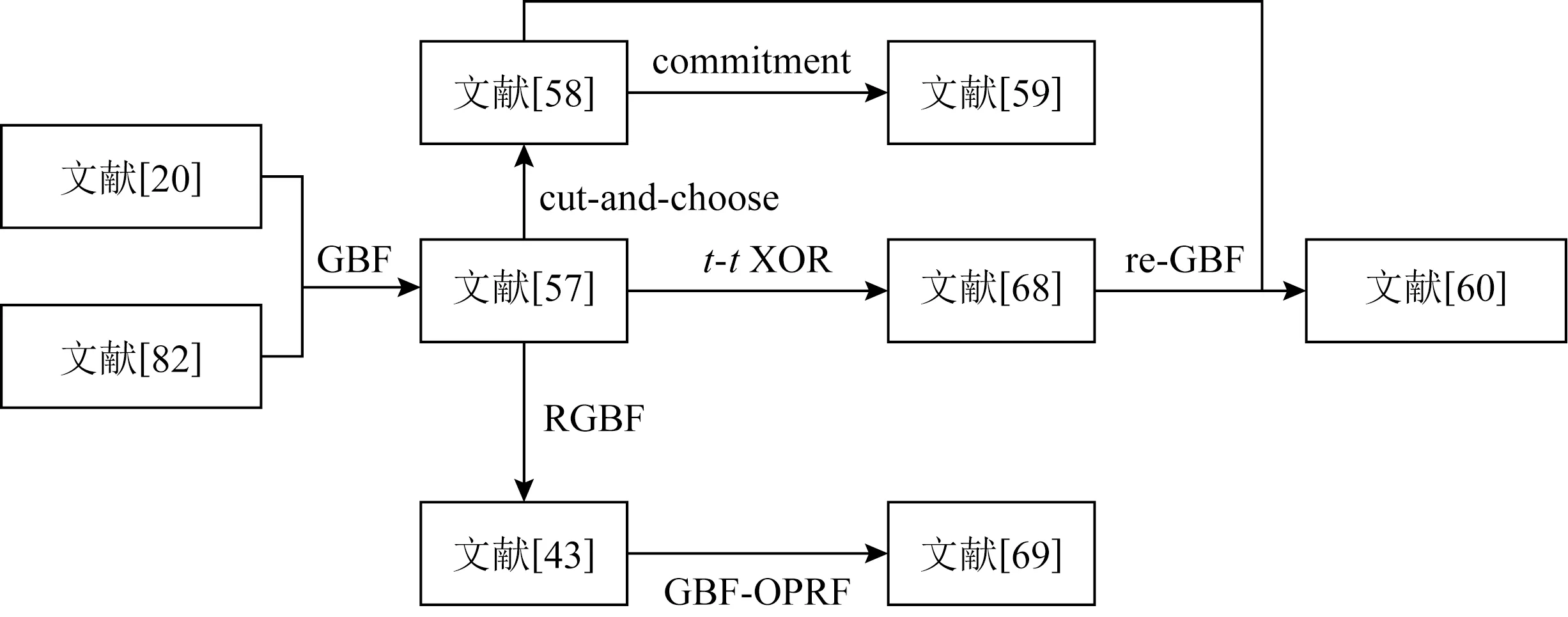
Fig. 3 The progress of BF based PSI protocols图3 基于BF的PSI协议进展

Dong等人[57]首先通过BF构建PSI:双方根据其私有集构造BF.双方执行OT协议，P2获得P1中BF为1的索引.最后P2通过计算2个BF上的逐位与操作，得到交集结果.但其泄露了P1的BF中为1但不属于交集的额外信息.由此进而提出混淆布隆过滤器GBF，将元素x首先拆分为k个共享值并通过hashk映射得到k个BF索引，并将k个共享值随机填充，将BF中的每1比特信息改为1个随机字符串.GBF插入元素x步骤:计算hashk，共用GBF中已有字符串，剩下的位置通过异或得到共享字符串并填充入对应位置.基于GBF的隐私集合交集:P2根据私有集合构造BF，P1根据私有集合构造gbf1和随机填充gbf2.P2测试元素x是否属于P1的私有集合执行为:双方执行m个1-out-of-2 OT(m为BF长度)，P1输入消息对(gbf1,gbf2)，P2输入BF作为选择位，P2只能获得gbf[hi(x)]，i∈[1,k].然后P2将k个gbf[hi(x)]进行重组与x比较即可完成测试.

Rindal等人[58]通过生成比所需的BF比特数略多的1-out-of-2 OT构建Cut-and-Choose技术以此实现抵抗恶意敌手的PSI协议:P1从OT中随机抽取一小部分，让P2证明适当数量的OT中使用了选择位0.然后再进入在线阶段，执行离线阶段未使用的OT协议.

Pinkas等人[43]基于随机OT扩展设计了1个不经意伪随机发生器(oblivious pseudo random generator, OPRG)以完成GBF的构建:双方基于私有集构建BF,分别为bfx和bfy，将bfx和bfy的每一个对应比特bx,by作为OPRG的输入.OPRG产生1个随机字符串发送给bt=1(t∈{x,y})的参与方构建出gbfx和gbfy.对集合X的每一个元素xi，P1计算m1[i]=gbfx[h1(xi)]⊕gbfx[h2(xi)]⊕…⊕gbfx[hk(xi)].P1将m1打乱并发送给P2，P2通过检查是否存在1个i使得m1[i]=gbfy[h1(yi)]⊕gbfy[h2(xi)]⊕…⊕gbfy[hk(yi)]判断元素yi是否为交集.相比于GBF，OPRG具有更小的通信量和计算量.

Inbar等人[68]通过秘密共享将文献[57]扩展为多方PSI协议:每个参与方Pi通过hashk本地生成GBF和BF.然后参与方Pi选择t个随机字符串共享GBF，将字符串分发给其他参与方，以完成在所有各方之间(t,t)异或秘密共享其GBF.Pi将其接收到的所有GBF的共享字符串异或后，得到新的GBF再将其发送给P0.P0对所有的GBF进行异或再和本地BF异或得到交集.Zhang等人[59]使用星型拓扑结构[46]和Cut-and-Choose[58]技术实现多方恶意安全的PSI.协议通过离线-在线阶段的方式进一步优化，将多数繁重的计算、通信放在预计算阶段.

Karakoç等人[69]继承文献[54]的设计思想，通过布谷鸟Hash算法构建2维表，再对每个桶运行PSM协议，执行比较协议并完成具有可计算对称函数的电路PSI.文献[68]通过修改文献[57]的结构，设计了基于BF的PSM:显著降低了通信量，且不再使用电路进行等值比较，而是将PSM通过控制参与方只输入1个元素得到PET，执行PET使得等值测试不消耗任何通信量.

Efraim等人[60]改进了恶意安全的两方PSI协议[58]结合半诚实安全的多方PSI协议[68]构造出高效的恶意安全的多方PSI协议.首先为解决直接结合协议造成通信量随参与方数量的增加而指数增长的问题对恶意两方协议[58]进行了改进:通过P2和P1执行k-out-of-NOT，使得P2获得P1的GBFG1的适当部分.然后引入重随机化GBF的概念，P2重随机化GBF得到reGBF.双方再次执行k-out-of-NOT，其中P2和P1角色互换，让P1获得P2的reGBF适当部分，该过程避免了直接发送GBF而泄露P1不在交集的元素信息.最后P2通过比较reGBF和自身GBF得到隐私集合交集.为将两方协议推广到多方协议，首先让P0与每一方Pi执行2次k-out-of-NOT协议，OT执行之前先执行Cut-and-Choose技术以抵抗恶意敌手，然后P0将其得到的所有GBF进行异或操作得到GBFG0.同时Pi与P0交互得到的GBF和自身GBF异或得到Gi.最后为克服Pi直接将Gi发送给P0使得P0可以获得与每一方的交集问题，所有参与方需执行t-t秘密共享Gi，并将得到的份额求和再发给P0，求得多方交集.

4 新型场景的隐私集合交集

4.1 非平衡PSI

传统PSI的大部分方案往往要求参与方集合的大小相等或相近，并且假设了双方具有相似的计算和存储能力，称之为平衡PSI.然而，在某些实际应用中，如隐私联系人发现，客户拥有几百到几千个联系人集合，而服务方拥有百万甚至千万级的用户集合，它们的集合大小不平衡，技术能力和存储空间也相差甚远.使用平衡PSI协议，它们的通信开销和计算开销均与较大集合成线性关系，导致客户端需承受巨大的存储与计算开销.这激发了对不平衡PSI的研究.

目前，只有少数研究考虑了集合大小不对称的情况:Chen等人[86]使用同态加密将大小为N的集合的通信量减少到O(logN).接收方加密集合并将其发送给发送方，发送方通过计算适当的比较电路来计算同态加密数据的交集.使用同态乘法将输出压缩到更小的尺寸，并发送回接收方进行解密.在协议中，接收方只执行相对较轻的计算，当接收方的计算能力有限时(如移动设备)，该协议十分有效.在此基础上，Chen等人[87]使用OPRF预处理阶段来实现比文献[86]更高的性能和安全性，实现了针对恶意客户端和恶意服务器的安全性，并将集合求交扩展到带标签PSI的特殊用例，其对于相交元素传输相关联的标签.协议的优点是它们的通信复杂度是次线性的，而不是服务器集合大小的线性，然而，协议的缺点是以重复的高计算开销作为代价.

Kiss等人[88]描述了一种将O(N)通信量放在预处理阶段的方法，其中服务器为每个元素x发送包含AES(k,x)的大型Bloom过滤器.各方使用Yao协议来对客户端的每个元素上的AES进行模糊评估，客户端可测试Bloom过滤器的成员资格.即服务器只能对其数据执行1次操作，并将结果发送给客户端，客户端将在未来的执行中使用它们来计算交集.Resende等人[89]设计了一个更节省空间的布谷鸟过滤器用于服务器预处理阶段发送大消息，以节省存储和通信成本.为了进一步减少通信，发送方将集合X转发给接收方之前对其进行压缩.虽然这种压缩确实减少了通信，但在高压缩率下产生误报，接收方以不可忽略的概率输出YX中的元素.

Resende等人[90]通过基于排名和选择的商过滤器(rank and select based quotient filter, RSQF)来减少协议交换的数据量，相比其他数据结构具有更小的存储空间，支持删除、插入、查找、合并等操作，当集合达到最大容量时可重构过滤器，而无需从头开始生成新的过滤器，在隐私联系人查找等应用场景具有重要意义.文献[90]将RSQF数据结构引入PSI协议中，通过放宽常数时间执行加速椭圆曲线提高协议计算性能.离线阶段，服务器对元素使用插入操作生成RSQF，并将RSQF发送给客户端.在线阶段，客户端和服务端进行交互以掩盖客户端元素，客户端通过查找操作判断它的元素是否属于RSQF，从而得到集合的交集.

在最近的研究中，Lv等人[91]研究了在不平衡场景下计算集合交集的基数，利用Bloom过滤器构造低通信复杂度计算非平衡私有集合交集基数.接收方不需要用低功耗设备加密发送方的数据集，当接收方的数据集比发送方的数据集小得多时，协议实现了高效率.

4.2 云辅助PSI

随着云技术的发展，基于云服务器的PSI协议逐渐成为热点.云服务器具有高计算能力和存储容量，为现有的PSI协议提供了成熟的优化方法，但又产生了数据外包的隐私泄露问题.基于云辅助的PSI协议可分为数据加密和数据盲化2种.

Kerschbaum[92]提出服务器代理其中一个客户端A与另一个客户端B利用单向函数实现PSI操作，且代理是一次性.之后，Kerschbaum[93]提出将2个客户端的BF通过同态加密外包给云服务器而不是对数据本身加密外包给服务器，服务器进行PSI操作.客户端只需本地保留集合元素以验证得到的交集BF里包含的本地元素.Liu等人[94]直接利用对称和非对称加密方案对数据集加密并外包给云服务器，云服务器每进行一次PSI操作时，客户端都需下载加密向量，且会向服务器泄露交集基数.Kamara等人[95]基于伪随机密钥对集合元素进行盲化处理再发送给云服务器，但交集计算任务仍在客户端中进行，服务器只为某一个客户端重新编码集合来维护计算隐私性.Qiu等人[96]将隐私集合求交计算完全委托给服务器，但需要确保服务器可信，因为云服务器可不经客户端同意进行PSI计算并得到交集基数.以上基于云服务器的PSI协议并不能完成云服务器的理想功能，如数据集仍需本地存储、数据需反复上传下载、PSI计算不能完全委托给云服务器等.

Abadi等人[47]提出O-PSI，利用点值多项式和Paillier同态加密实现将隐私集合求交操作完全委托给服务器，无需本地维护集合，客户只需上传1次外包数据集即可应用到多次隐私集合交集计算的理想云服务器功能，但是其方案基于公钥密码操作，过于昂贵.Abadi 等人[97]提出基于Hash表和点值多项式表示集合构造了一种即具有云服务器理想功能又无需公钥操作的高效PSI方案，称为EO-PSI.但各方之间需事先建立安全通道，否则攻击者可以窃听隐私信息.Kavousi 等人[98]提出无需安全通道的改进协议.O-PSI理想云服务器功能构造为:客户端A，B为伪随机函数选取随机密钥k.构造多项式点值对{(x1,y1),(x2,y2),…,(xn,yn)}表示集合，将由yi组成的向量Y=(y1,y2,…,yn)通过随机值ri=f(k,i)进行盲化，得到向量v=(y1r1,y2r2,…,ynrn)发送给服务端.客户端若同意云服务器计算交集，则客户端B使用Paillier加密盲化值，发送给客户端A，A再对其加密发生给服务器.最后服务器利用加法同态性质进行PSI操作得到向量T将其发送给客户端B，客户端利用私钥解密得到由yi(A)和yi(B)组成的zi，最后通过点值对(xi,zi)进行多项式插值得到交集元素.

李顺东等人[99]在云计算环境下设计了多方隐私集合求并(求交)方案.通过输入集合域已知的1-r编码(0-r编码)将求并(求交)集合表示为向量，借助哥德尔编码将向量编码为自然数x，利用同态加密得到密文E(x)以防止泄露明文，利用模运算对密文进行秘密共享以防止云服务器合谋，利用模运算性质对所有密文相乘再通过算术基本定理展开得到并(交)集集合，但方案限制了输入集合的范围以及不能进行两方计算.

Abadi等人[100]提出支持外包数据集有效更新和可扩展的多方隐私集合求交协议Feather，允许客户端只上传1次私有数据集即可无限次委托计算，无需公钥密码操作使其具有高效率和高可伸缩性.协议由3部分组成：1)设置阶段.客户端构造Hash表并为每个桶生成1个多项式、BF和标签，利用伪随机函数盲化BF，并随机排列桶、盲化BF和标签.客户端保留标签到桶的映射和排列，向云发送置换的桶、BF和标签.2)更新阶段.客户端利用Hash函数确定更改集合元素所在桶，计算桶的标签将其发送给云，云将标签对应的桶和盲化BF发送给客户端，客户端利用密钥恢复桶的内容对其进行重新编码然后将更新的桶和过滤器发送给云服务器.3)PSI计算阶段是基于文献[97]的改进.

Debnath等人[101]利用BF、乘法同态加密、零知识证明-数据签名结合技术设计了一种抵抗恶意敌手的O-PSI结构.协议实现了标准模型安全且取得了较低的线性复杂度.协议包括1组客户端{C1，C2,…,Cn}和1个云服务器S.如果客户端Ci想要学习和Cj的交集.Ci通过签名消息对请求Cj许可，如Cj许可则将签名消息对发送给S.S计算结果集并将结果集和从Cj收到的签名消息对发送给Ci.最后Ci在本地计算交集结果.

Ali等人[102]基于属性基加密的思想提出属性基私有集合求交 (AB-PSI) 方案，可提供细粒度的访问控制，并允许数据拥有者通过定义访问控制策略控制其外包数据集的访问权限，实现数据拥有者不参与的情况下完成PSI操作，云服务器通过隐私集合交集访问权限和盲化后数据集计算出相应的访问权限.如果请求交集的客户端能得到一个有效的访问权限，则可计算出其数据集和请求数据集的交集.Shi等人[103]基于密钥策略属性加密(key-policy attribute-based encryption, KP-ABE)和PSI相结合提出一个新的概念:基于委托密钥策略属性的外包加密数据集交集(KP-ABPSI)，以实现隐私集合交集计算完全委托给云服务器和对PSI的细粒度访问控制.集合元素d被加密为2部分：第1部分和元素d本身相关，进行加密盲化；第2部分和访问控制策略相对应的属性集相关.数据用户生成与第2部分相关的令牌，一旦令牌满足访问控制权限，云服务器就能得到d被加密的第1部分，最后进行PSI操作将结果返回给数据用户，数据用户对其解密得到交集元素.

4.3 阈值PSI

阈值PSI指当交集的基数大于或等于门限值时，接收方才能获得隐私集合交集.如网约顺风车，在不泄露陌生人路径的情况下如何共享双方的公共路径是该场景的重点问题.

Hallgren等人[104]通过构造门限密钥封装机制，实现交集的基数与阈值隐私比较，从而得到TPSI. Zhao等人[105]基于不经意多项式评估构建了1个加密私有集合交集基数(ePSI-CA)协议，通过外包扩展使协议更接近于现实世界的模型.以上TPSI协议首先计算交集基数，再比较其与阈值t的关系考虑是否执行PSI协议，其通信复杂度依赖于集合的大小.

Ghosh等人[106]提出了第1个通信复杂度仅依赖门限t的PSI协议，其通过测试两集合是否足够相似而非计算交集基数.其基于较弱假设，计算效率高但通信复杂度为O(t2)，具体思想为：双方将集合各自编码为多项式，将两多项式相除，消掉相同项得到阶数更低的有理函数，通过比较有理函数阶数和阈值来判断是否执行PSI协议.Badrinarayanan等人[107]设计了2种多方TPSI协议，其通信复杂度随集合差的增大而增加，当集合差值明显小于集合大小时，该协议具有次线性通信复杂度.Branco等人[108]基于门限加法同态加密方案提出了一种新的允许N方检查其输入集的交集是否大于N-t的TPSI方案，该协议通信复杂度为O(NT2).

Mahdavi等人[109]介绍了另一种TPSI场景:多方分别持有1个集合，希望了解哪些元素至少出现在t个集合中，而其他信息不被泄露，称为超阈值多方PSI(OT-MP-PSI)，通过构造不经意伪随机秘密共享(oblivious pseudo-random secret sharing, OPR-SS)实现OT-MP-PSI协议，其通信复杂度为O(nmk).共享阶段:密钥持有方持有密钥k和值S，以及一组参与者Pi持有输入集合Si.每个参与方Pi输入Si和随机值ri，得到共享集合.由于具有OPRF的安全性，保证参与方Pi不知道密钥k，密钥持有者不知道集合Si.重构阶段:参与方将共享集合构建为Hash表并发送给重建者，重建者对所有的参与方选择t个执行拉格朗日插值验证每一行的元素是否大于等于阈值t，然后将其发送给参与方.此过程重建者无法知道元素S(i)，但参与方可以知道自己的哪些集合元素至少出现在其他t-1个集合中.

Zhang等人[110]基于GBF和秘密共享构建了一个新的TPSI，其通信复杂度为O(λm)，通过设计一种新的GBF来建立集合元素和秘密共享之间的关系，并使用其作为TPSI的门限检测，并通过秘密关系方案确定|X∩Y|和门限t的关系，只有当交集中有足够的元素时接收者才能重构秘密共享方案的多项式以获得交集.结合Reed-Solomon编码算法改进了秘密共享的重构阶段，通过忽略错误的共享而避免计算所有可能的共享组合重构秘密的可行方法.

4.4 多方PSI

隐私集合交集目前存在的高效协议大多只针对两方设置，多方PSI的高效协议并没有引起多大关注.这可能与各方之间不可避免的通信而导致极大的通信成本有关.目前关于多方设置的PSI协议大多采用2种网络模型:1)星型拓扑网络结构减少双方之间的中间交流，但给指定方带来了很高的工作量.2)星型-路径网络结构其使每一方(除指定方)的通信量和计算复杂度仅取决于自身输入集大小.还可能与如何保证只能获得所有参与方的集合交集，而不能获得部分参与方的集合交集有关.目前多方PSI协议主要通过秘密共享解决该问题，使得只能秘密重构交集元素.Kolesnikov等人[62]通过指定方与各方执行OPPRF协议实现交集元素的零共享，Hazay等人[46]通过构造门限同态加密方案实现元素的零共享.零共享指如果所有各方都持有相同的值x，共享异或得到0，否则得到1个随机值. Inbar等人[68]、Efraim等人[60]利用GBF和OT实现元素秘密共享.Kavousi等人[70]不再对集合元素进行秘密共享而是对密钥进行秘密共享，通过路径结构，逐一得到由密钥k加密的OPRF值，指定方对OPRF值进行比较得到交集结果.为了对上述提到的多方协议性能有更加深刻的认识，从通信量(指定方，其他方)、计算量、安全模型、设计思想及隐藏技术、网络结构等方面总结如表3所示:

Table 3 Complexity Analysis for Multiparty PSI表3 多方PSI复杂性分析

5 总 结

综上所述，随着安全多方技术研究的逐步深入，PSI作为安全多方计算的一种重要应用，已被广泛应用于隐私计算，具有重要的理论和实践意义.首先介绍PSI协议的密码技术、敌手模型、安全证明、编程框架，其次系统总结了传统PSI协议的密码框架，随后介绍PSI协议中集合元素比较技术，进一步地详细阐述了适应新型应用场景的PSI方案.随着密态数据的隐私计算技术进一步深入，传统的PSI在安全性、高效性、适用性、可扩展性等方面受到了巨大的挑战.因此，未来的主要研究方向建议在4个方面:

1) 考虑威胁性更高的场景，设计不同安全性需求的PSI协议.在目前主流PSI协议设计中，通常只考虑半诚实的敌手.然而在协议执行过程中可能会有黑客等侵入、篡改甚至伪造数据，因此需将半诚实模型推广到恶意模型，协议需要保证在恶意攻击下仍然使得数据具有一致性与可用性.

2) 考虑更多的参与方，从而增加适用范围.传统的PSI协议一般只有2个参与方(即发送方和接收方)，而两方PSI协议所使用的技术在一般无法简单推广至构建多方PSI协议，且会导致部分隐私数据的泄露，多方PSI协议允许多个参与方共同计算所有参与方的交集，这使得问题的难度进行了提升，也增加了PSI协议的适用范围.

3) 面向新型场景构建PSI协议.在某些特定场景中，通过PSI协议得到的交集元素仍然是敏感信息，如电子医疗中的病患数据、基因测序中的序列数据等，需要对现有PSI协议进行改造，允许参与方在交集保密的情况下对交集中的元素进行各种函数的运算，如计数、求和等.

4) 提高现有方案的效率.目前大部分的PSI方案都是复杂的密码学操作，如基于全同态加密、不经意传输、混淆电路、公钥加密等，计算或通信开销随数据集大小呈现线性增长.目前PSI协议在百万数据集下的运算速度尚能接受，但当数据集大小达到百亿数量级时，传统的PSI方案效率会大幅度下降，迫切需要构建面向海量数据的高效PSI协议，实现数据的共享.