基于空气-雪两相流动力学仿真的滑雪板界面特性及其减阻性能研究

廖章文 ,张胜年 ,魏书涛 ,张成蛟 ,姜 峰*

(1.华侨大学 制造工程研究院,福建 厦门 361021;2.脆性材料产品智能制造技术国家地方联合工程研究中心,福建 厦门 361021;3.上海体育学院,上海 200438;4.三六一度(中国)有限公司,福建 厦门 361009;5.南通大学 安全防护用特种纤维复合材料研发国家地方联合工程研究中心,江苏 南通 226019)

从1924年举办第一届冬季奥林匹克运动以来，比赛项目不断发展，到如今2022年北京冬奥会比赛项目逐渐趋于完善，设有7个大项，15个分项，109个小项[1-2].其中，15个分项中，冰上项目有5项：冰壶、冰球、花样滑冰、速度滑冰和短道速滑；雪上项目有10项：自由式滑雪、冬季两项、越野滑雪、跳台滑雪、北欧两项、无舵雪橇、有舵雪橇、钢架雪车、单板滑雪和高山滑雪[3].从项目比例来看，雪上项目占三分之二的比重，其重要性显而易见.雪板是雪上项目的重要装备，分为单板滑雪板与双板滑雪板.其中，与单板滑雪相关的项目有U形场地技巧、大跳台、障碍追逐及平行大回转等，与双板滑雪板有关的项目有高山滑雪、自由式滑雪、越野滑雪和跳台滑雪等[4].历年的冬奥会，我国的冰上项目成绩都远高于雪上项目，但在2022年北京冬奥会中国雪上项目奖牌数量首次超越了冰上项目，实现突破，未来雪上项目的发展潜力依旧巨大.

在滑雪运动过程中，影响比赛成绩的因素除了运动员自身技巧与环境外，滑雪板与雪滑动界面的作用力、滑雪板的结构和位姿以及滑雪服等同样是不可忽视的影响因素[5].单板滑雪更倾向于技巧性竞技，因此，对于涉及单板滑雪板空气流体的研究文献较少.目前，研究人员进行的研究主要在雪板设计原则与方法和雪板与雪的界面作用机制方面.在雪板设计原则与方法方面，Brennan等[6]建立了滑雪板的力学特性和雪地性能计算模型，利用“Snowboard-MECH”和“Snowboard-TURN”计算代码比较不同滑雪板的力学性能和雪地性能，将这两种计算代码的输出和实验室数据以及滑雪板运动员完成规定s形路线所产生的数据进行比较，验证这两种代码.结果显示，模型生成的结果与数据一致，为模型和相应的计算机代码提供支持.此过程描述了1个程序，通过该程序可将研究中的计算机代码应用于滑雪板设计中.单板滑雪板与尾波板结构设计上存在相似之处，Poodts E等[7]对尾波板的入水(攻角)问题进行试验与数值模拟研究，为夹层结构尾波板的损伤容限设计提供可使用的计算公式.数值计算结果表明，由于流固耦合作用，板的最大变形存在1个极限，即使在高能量的冲击下也不会超越这个极限，这也限制了尾波板在入水过程中达到的最大冲击应力，从这一数据结果出发，利用经典夹层理论的解析公式得出设计变量之间的数学关系，为尾波板的结构设计提供可靠的规则.Yang等[8]根据比赛得分标准、运动员在空中的动作以及空中的高度判断，找出运动员获得高分的最佳方法，设计了一种新的滑雪板赛道(半管)形状，最大限度地延长了空中“飞行”时间，并通过数学计算优化运动员在空中的位姿.

在雪板与雪的界面作用机制方面，研究学者对界面减阻作用机制进行研究，Wu等[9]发现高灵敏的红细胞在紧密贴合的毛细血管中移动，摩擦阻力非常小，由于法向力几乎完全由高度可压缩糖萼层中的流体压力平衡，并且细胞与固相之间的滑动摩擦阻力非常小.这种红细胞在内皮糖萼层上的运动与滑雪板在雪面上的运动之间存在相似性，由于多孔层中滞留的流体或空气无法快速溢出，在这种情况下会产生1个将滑雪板向上顶的升力，从而降低雪板滑动界面的作用力.在发现雪的这个特性后，研究人员对雪的渗透性[10]、压实应用[11]、界面摩擦特性[12]以及多孔介质中流体流动性[13-14]等方面进行研究，提出可压缩多孔质广义润滑理论，为理解柔软多孔层对快速变形的详细动态响应奠定了基础.在工程设备上也有雪颗粒对空气流向影响的研究，Dinc等[15]利用计算流体力学(CFD)的方法设计导流板，并采用离散相模型(DPM)对雪粒子进行计算研究，分析雪粒子从导流板和卡车上反弹后的运动轨迹.结果显示经过重新设计后的导流板能在很大程度上减少发动机格栅和挡风玻璃的积雪.同样，Zhang等[16]采用雷诺平均Navier-Stkes (RANS)方程，结合Realizablek-ε湍流模型和拉格朗日粒子相法，对火车转向架区域的空气-雪两相流进行了数值模拟.针对三种典型的偏转板迎角(30°、60°和90°)进行研究，结果表明60°工况下，积雪减少效果最佳.

雪板与雪的接触界面涉及空气-雪两相流的影响，如图1所示.结合已有文献对雪的特性与雪对空气流向的影响研究，可以发现空气-雪的两相相互作用会间接影响滑雪板滑动界面的作用力，因此，对于滑雪板结构参数和攻角的优化研究就显得非常必要.本文中从宏观尺度进行仿真，不关注雪颗粒本身与雪板的相互作用，采用传统纯CFD仿真的方法，将空气与雪看作两种不同的流体(混合流体).此两相流体，其中一相按照空气参数设置，另一相按照雪参数设置，对雪板进行结构与位姿的优化，提升运动员在斜坡加速阶段的速度，进而增加腾空的高度，从而使运动员拥有更多的时间来完成比赛动作.因此，选择作用力为考量标准，并给出优化后的雪板设计方案.

Fig.1 Diagram of air-snow flow (Chinese snowboarder Su Yiming competing at the Beijing Winter Olympics)图1 空气-雪流动示意图(我国单板滑雪运动员苏翊鸣在北京冬奥比赛中)

1 模型建立

1.1 滑雪板结构及其三维建模

单板滑雪是以板为工具，在规定的线路上快速回转滑降，在各种不同的障碍赛道上竞速、飞行、跳跃及翻腾的一项雪上运动[17-18].滑雪单板主要的结构参数包括有效板刃、板头板尾、侧刃半径和单板弧形(拱形)等，如图2所示.

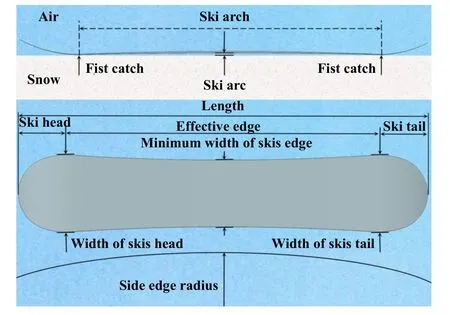
Fig.2 Schematic diagram of snowboard construction图2 单板滑雪板结构示意图

本研究中对张家口京禧品牌的单板滑雪板(EMP-159)进行UG三维建模，如图3所示.

1.2 理论模型

1.2.1 控制方程

通过CFD仿真分析，提取相关的物理量用于滑雪板参数优化.其中，滑雪板的宏观作用力主要包括正压力和剪切力，正压力和剪切力的合力影响雪板的阻力.微观作用力主要是界面上的黏滞力，黏滞力影响雪板的稳定性[19].本文中采用雷诺时均方法进行模拟，可实现滑动界面上的复杂外部流动模拟.使用k-ε模型与k-ω模型[20]，其中，k-ε模型为半经验公式，需要求解模型公式中的湍动能与其耗散率方程，适用于完全湍流的流场模拟；k-ω模型主要应用于壁面束缚流动和自由剪切流动，其控制方程如下文所示.

质量守恒方程如式(1)所示.

动量守恒方程如式(2～4)所示.

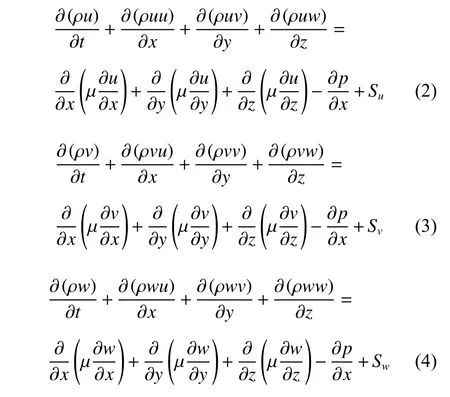
式中：p是压力；常数μ是动力黏度；u、v和w是流体在t时刻x、y和z方向上的速度分量；Su、Sv和Sw是广义源项，式(2)、(3)和(4)又称Navier-Stokes方程，简称N-S方程.湍流能k和耗散率ε关系如式(5)和式(6)所示.

式中：ρ是流体密度；Gk表示由层流速度梯度而产生的湍流动能；Gb表示由浮力产生的湍流动能；YM表示由在可压缩湍流中过渡的扩散产生的波动；C1ε、C2ε和C3ε是常量；σk和 σε是k方程和ε方程的湍流Prandtl数；Sk和Sε是用户自定义数据.

SSTk-ω模型流动方程如式(7)和式(8)所示.

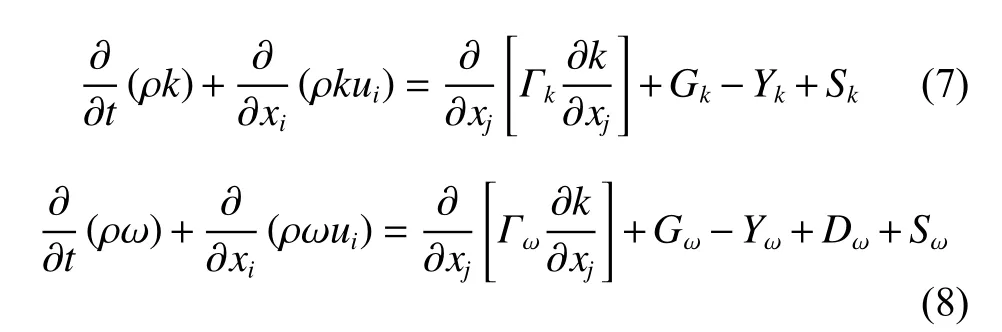
式中：Gk表 示湍流的动能；Gω为ω方程；Γk和 Γω分别代表k与ω的有效扩散项；Yk和Yω分 别代表k与ω的发散项；Dω代 表正交发散项；Sk与Sω是用户自定义.

k-ε模型和SSTk-ω模型的变形增长在于综合了混合功能和双模型，混合功能主要是为近壁区域而设计的.

1.2.2 合力的计算模型

(1)绝对压力

绝对压力Pabs是静压力、参考压力和存在重力时的流体静压力之和.

(2)相对总压力

相对总压力是流体在绝对坐标系中处于静止状态所导致的压力.

(3)绝对总压力

绝对总压力Pt,abs是流体在绝对坐标系中处于静止状态所导致的压力.对于理想气体，绝对总压力的表达式如式(9)所示.

其中：γ为比热比，M为马赫数.

对于不可压缩流体，绝对总压力是绝对压力和动压的总和，如式(10)所示.

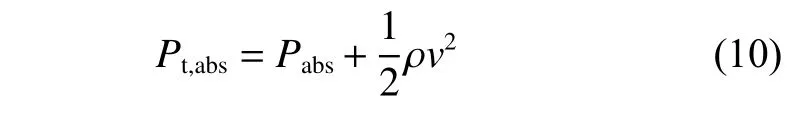
(4)总压力

总压力Pt是 绝对总压力减去参考压力和存在重力时的流体静压力，如式(11)所示.

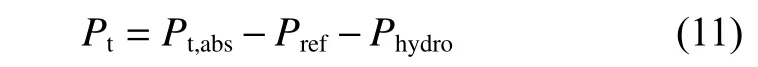
对雪板表面的压力分布进行积分得到正压力方程，如式(12)所示.

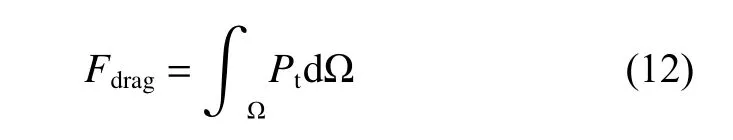
式中：Fdrag为正压力；Ω为雪板的表面积.

(5)表面上的剪切力计算，如式(13)所示.

其中：T为面上的应力张量，a为面网格面积矢量.此剪切力通过流体施加在表面上.

(6)黏滞力的计算

黏滞流体绕物体流动，求解阻力基于附面层理论，普遍采用的是附面层的积分方程.附面层的积分方程是根据动量定理，作用在控制体上所有作用力的合力等于单位时间流出和流入控制体动量之差.若附面层内流体未脱体时，黏滞力式则可由导出的附面层方程式求解，如式(14)所示.

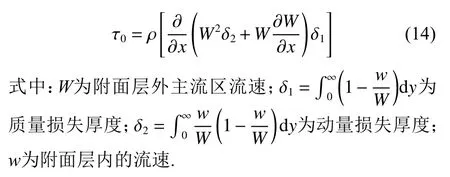
该公式适用于层流附面层和湍流附面层.对方程进行分析求解得到τ0的相应计算式.但是，当附面层内流体脱体时，则τ0≈0. 这时，流动阻力以净压力 Δp为主，而 τ0可忽略不计，净压力即绕流模型前后的压力差.若能保持附面层内流体不脱体，即黏滞力较小为佳.

1.2.3 仿真模型的建立

根据滑雪板整体大小确定计算区域的尺寸，其中长2 000 mm、宽820 mm、高715 mm，由于滑雪板模型是1个完全对称模型，因此，为减小网格生成和计算工作量，提高效率，将流场计算域进行对称分割.采用ANSYS的Fluent模块对计算区域进行四面体网格的离散化.空气-雪的流动模拟研究需要得出空气与雪的可流动空间，因此要进行Boolean求差运算，将在外围建立的流场减去内部的滑雪板，剩下空间为空气与雪的可流动区域，如图4所示.滑雪板模型的表面网格精度为0.5 mm，越靠近滑雪板表面的网格越细，更能精确地呈现空气与雪的混合状态，而远离滑雪板的位置网格较粗.生成的网格总数大约在四百万左右，如图5所示.

网格设置后，进入Setup界面，先是将多相流模型设置为Volume of Fluid，然后将欧拉多相流数目设为两相，再将VOF Sub-Models一栏中的Open Channel Flow选项勾选上.接着打开黏性模型对话框，在k-ε模型中选择可靠性高的模型，在Near-Wall Treatment中选择Non-Equilibrium Wall Function，在k-ω模型中选择SST选项，完成多相流模型的设置.

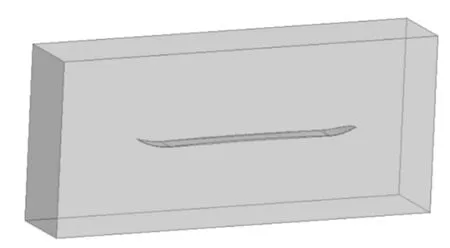
Fig.4 Schematic diagram of calculation area图4 计算区域示意图

Fig.5 Grid distribution diagram图5 网格分布示意图

在设置流体材料时，由于是空气-雪两相流的仿真，因此需要将两种材料分别进行属性赋值，空气本身存在于ANSYS软件材料库中，可直接调取.雪这种材料在库中并不存在，则需要根据其性质进行材料参数设置.通过查阅Dinc等[12]有关ANSYS雪仿真的材料参数设置，将比热容设置为2 100 J/(kg·℃)，比重设置为100 kg/m3，材料的相对分子质量设置为18.02，初始温度设置为263 K，将黏度设置为1×10-2Pa·s.

1.2.4 边界条件与工况确定

边界条件设置如下：(1)滑雪板的初始位置为下沉入雪中2 mm；(2)流速设置为10 m/s；(3)空气部分的压力为标准大气压；(4)重力常数设置为g=9.807 m/s2；(5)气体为不可压缩的空气.

本研究中将开展四种滑雪板结构参数变量设置和滑雪板在5个不同攻角下雪上运动过程中的流动特性的CFD优化研究.其中，根据国际滑雪联合会(FIS)最新发布的2020～2021年版的比赛装备规则，对滑雪板的结构参数进行变量设置.原雪板模型参数：侧刃最小宽度为230.5 mm，侧刃弦长为1 050 mm，板身拱形高度为6 mm，板头翘曲高度为54.5 mm，板尾翘曲高度为45 mm，速度V=10 m/s.滑雪板结构参数变量设置：侧刃最小宽度±2 mm；侧刃弦长±1.5 mm，板身拱形高度±1.5 mm，板头及板尾翘曲高度±1.5 mm，滑雪板的攻角α值分别为-10°、-5°、0°、5°和10°，如图6所示.根据这些参数设置生成计算网格，分别进行CFD模拟.

2 结果分析与优化

2.1 不同雪板几何结构参数的优化

2.1.1 正交试验设计

Fig.6 Schematic diagram of ski posture and structural parameters图6 滑雪板姿势与结构参数示意图

滑雪板的结构优化设计涉及4个变量参数，每个参数存在3个不同的值，使得CFD仿真试验的试验模型量达到34=81个，模型数量比较大，会将试验的规模变大，因此，采用正交试验的方法进行.正交试验是一种利用正交表来安排与分析多因素试验的方法.因为本试验中仅仅考虑4个参数对滑雪板所受合力的影响效果，不考虑各个因素之间的交互作用，因此选用L9(34)正交表，这样仅需做9个模型，进行9次试验就可以找出最佳的滑雪板设计及最大影响因素，因素水平表见表1.将侧刃最小宽度、侧刃弦长、板身拱形高度和板头及板尾翘曲高度这4个试验因素分别记为A、B、C和D.

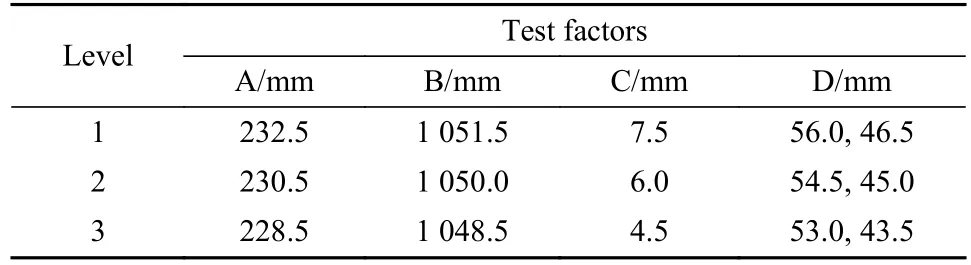
表1 因素水平表Table 1 Factor level table

根据正交试验表进行建模仿真，其结果列于表2中.

表2 正交试验结果Table 2 Orthogonal test results

2.1.2 结果分析

首先分析A因素，即侧刃最小宽度对试验指标的影响.A因素的1水平，命名为A1，其他以此类推.由表2可以看出，A1的影响因素体现在第1、2和3号试验中，A2的影响则体现在第4、5和6号试验中，A3的影响体现在第7、8和9号试验中.其中：y表示合力；K表示某一水平下，对应因素的试验结果；k表示K的均值.

A1所对应表现的试验指标之和为

A2所对应表现的试验指标之和为

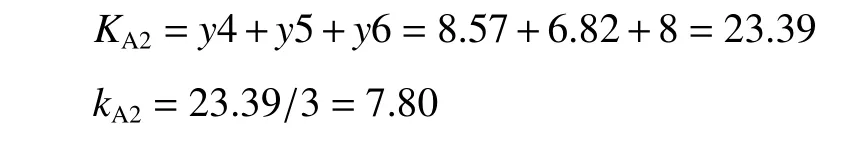
A3所对应表现的试验指标之和为

极差RA=8.15-7.80=0.35.同理，对B、C和D进行试验指标的影响分析，结果列于表3中.

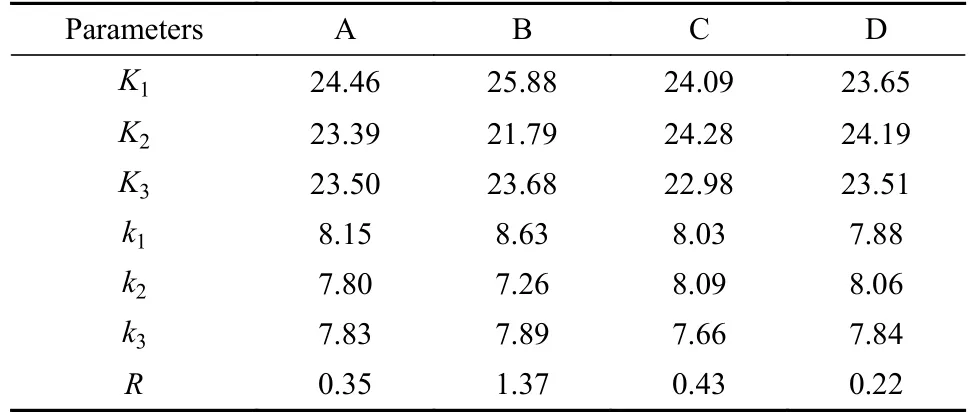
表3 指标的影响分析Table 3 Influence analysis of indicators

从表3中可以看到，极差R大小为B＞C＞A＞D，极差不相等，说明各因素水平改变对试验结果的影响不相同，极差越大，表示该因素的数值在试验范围内的变化会导致试验指标在数值上变动量更大，所以对极差影响最大的因素也是对试验结果影响最大的因素.因此，B因素对应的侧刃弦长是主要的影响因素.

根据正交试验的特性可知，对A1、A2和A3而言，3组仿真试验的条件完全一样，可以进行直接的比较.若因素A对于本试验的结果无影响，那么所得KA1、KA2和KA3的数据应该相等，但是由计算结果表明，KA1、KA2和KA3的数据并不相等.这说明A因素的水平变动对本试验的结果有影响，根据KA1、KA2和KA3的值可以判断因素A对试验指标的影响大小.此试验指标为合力，而合力越小对试验的结果越有利，因此根据KA2＜KA3＜KA1，可以判定A2为A因素的最优水平.

同理，对于B和C两个因素的最优水平分别为B2和C3.而D因素对试验结果影响最低，且D1与D3合力值非常接近，因此选择D1为最优水平.本试验4个因素的最优水平组合为A2B2C3D1，即侧刃最小宽度230.5 mm，侧刃弦长1 050 mm，板身拱形高度4.5 mm，板头及板尾翘曲高度分别56 mm和46.5 mm时滑雪板所受合力最小.此最优水平组合正好在正交试验时已经进行仿真，且合力的一半是9组中的最小值6.82 N.由此可以得到优化设计的单板滑雪板在雪与空气二相流体中所受的合力大约为13.64 N，相较于原始滑雪板的17.34 N，合力减少了21%.

2.2 雪板位姿仿真试验

滑雪位姿是1个整体概念，由膝部、臀部、背部和双臂等身体部位以及滑雪板位姿共同构成，其中滑雪板的攻角位姿直接影响滑动界面的空气混合状态，从而间接影响界面的合力.根据上文中优选出的5号滑雪板，进行不同滑雪板攻角α的仿真，得到雪体积分数的云图分布，如图7所示.滑雪板在尾部都会发生雪的飞溅，靠近板头的底板位置是空气与雪的主要混合区域.可以看到，当攻角为+10°与+5°时，滑雪板底部拥有更好的空气流入状态，将空气与雪最大化地混合，但在攻角为+10°时，板尾会形成扰流将飞出去的雪反向勾回，这不利于运动员发挥技术动作，且板底的空气更容易溢出，影响接触面的合力，而攻角为-5°与-10°时不利于空气进入雪板底部.

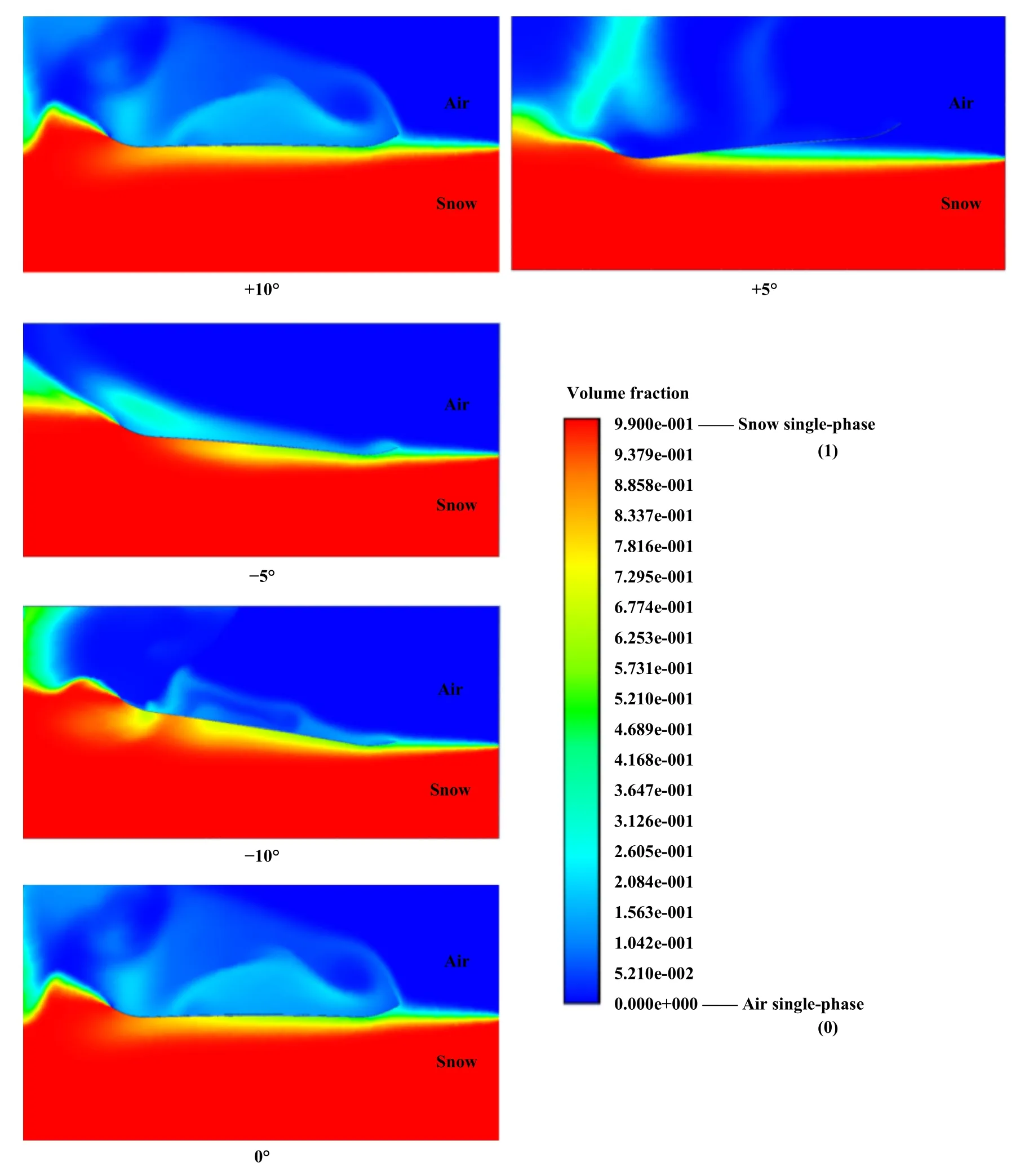
Fig.7 Cloud image of snow volume fraction (blue represents air phase,red represents snow phase,and the middle color change area is the mixed state of the two phases)图7 雪体积分数云图(蓝色表示空气相，红色表示雪相，中间颜色变化区域为两相混合状态)

不同攻角所产生的黏滞力变化曲线如图8所示，可以看出，当攻角达到-5°时，黏滞力达到最大，随着攻角的进一步增大，黏滞力呈下降趋势.

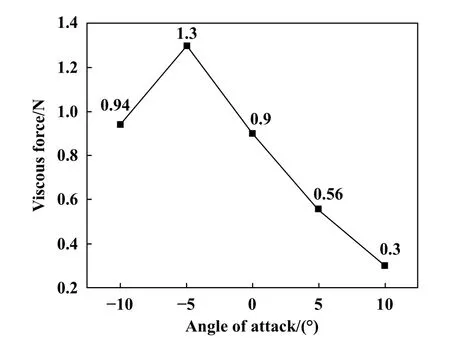
Fig.8 Viscous force results of snowboard simulation图8 滑雪板仿真的黏滞力结果

不同攻角所产生的合力变化曲线如图9所示，可以看到，总体的合力随攻角增大呈现出先减小后增加的变化趋势，所以并不是攻角越大，合力值就越低，在攻角为+5°时合力值达到最小，此时的合力值是攻角为-10°时的三分之一.

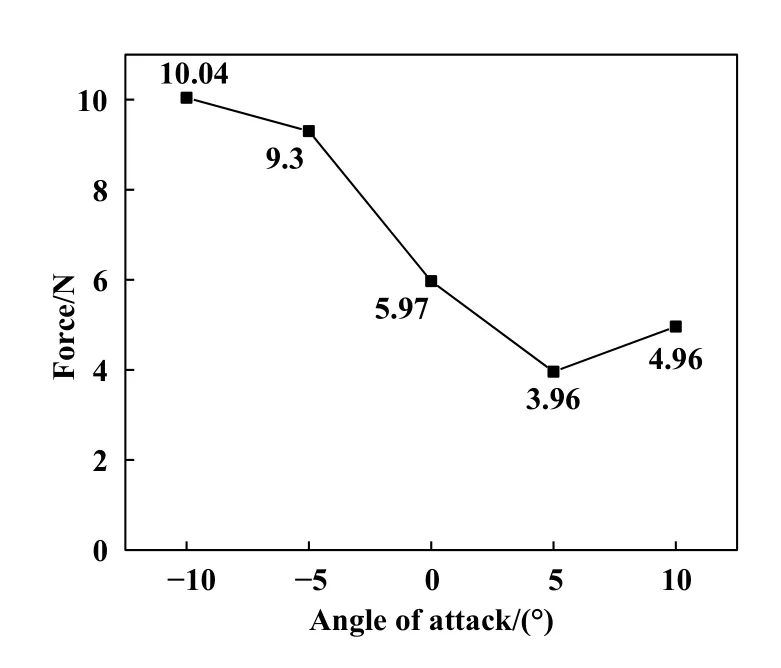
Fig.9 Resultant results of snowboard simulation图9 滑雪板仿真的合力结果

3 结论

a.本文中通过运用ANSYS软件的Fluent模块对滑雪板不同结构参数变量进行设置，并在不同攻角下进行仿真，得到单板滑雪板在滑行运动过程中受空气与雪两相界面作用下产生的合力影响，以合力为指标优化滑雪板结构设计.

b.通过对滑雪板的结构参数进行变量设置后仿真，并利用正交试验的辅助分析方法进行分析，发现侧刃弦长是4个因素中对界面合力影响最大.同时，找到4个因素中的最优组合为侧刃最小宽度230.5 mm，侧刃弦长1 050 mm，板身拱形高度4.5 mm，板头和板尾翘曲高度分别56 mm和46.5 mm时滑雪板与雪界面所受最小合力为13.64 N，相较于原始滑雪板17.34 N，合力减少了21%.可为后续的滑雪板设计提供参考.

c.运动员在短暂腾空结束后与雪面接触时，都会有一定的身体后倾，且滑雪板板头抬起，根据最优变量设置组合，对最优组合滑雪板进行攻角优化仿真，从仿真结果来看，抬起的攻角为5°左右时，黏滞力最低，滑动界面的合力最低，此为最优攻角参数，可对运动员运动过程中滑雪板位姿起指导作用.