某减压阀连接结构动态冲击模拟分析研究

薛 杰，张允涛，王 珺，李 锋

(西安航天动力研究所 液体火箭发动机技术重点实验室，陕西 西安 710100)

0 引言

航天系统中通常需要设计实现各种具体功能的控制阀来保证整个系统的正常运行。其中，减压阀就是一种压力调节装置，保证介质工作压力满足设计要求，在姿轨控动力系统上是一个重要组件。这对控制阀的固定连接结构提出了一个较高的要求，既保证产品在一系列服役环节中不出现错位、连接故障甚至接头结构破坏等问题，同时还要满足结构轻量化的要求。由于减压阀工作的力学环境恶劣，其连接结构往往都需要承受各种过载、振动、冲击等复杂严酷的力学过程，其中，冲击环境尤为突出。通过试验来研究减压阀固定连接结构在振动、冲击环境下的受力特性存在两方面问题：一方面是试验费用成本高、周期长；另一方面由于固定连接结构特征尺寸较小，常用测试设备和技术都无法完成有效测量，分析难于开展。因此，开展减压阀固定连接结构的冲击动力学仿真分析就显得十分重要。

近些年来工程上各种固定连接结构在工作过程或试验过程出现结构断裂的现象时有发生，许多学者对此也开展了许多研究。文献[2-8]对不同材料连接螺钉的断裂问题开展材料成分检测及断口分析，结果不同程度地表明热处理工艺不当将引起材料自身强度的大幅度下滑，并针对热处理工艺提出相应有效的改进措施。文献[9-11]通过数值仿真复现了连接螺钉结构断裂的位置，并指出了螺钉强度不足及载荷过大是导致结构断裂的主要原因。潘伟等分析了柴油发电机固定螺钉断裂失效问题，指出了应力集中过大及螺纹牙表面折叠缺陷是导致结构失效断裂的主要原因。刘春江等基于有限元分析对螺钉断裂失效进行研究，结果表明螺帽与螺孔周围的不良接触引起螺纹底部产生过高应力，从而导致螺钉断裂。文献[14-15]通过电子显微镜、测氢仪等测试手段对结构开展断口形貌、微观组织的分析，指出了热处理工艺不当会引起连接螺钉在服役过程中出现氢脆断裂。同样地，文献[16-17]通过金相检验、断口分析等方法指出断裂螺钉断口处具有明显的沿晶特征，属于疲劳断裂。

综上所述，学者们对连接结构的研究主要集中在连接结构的断口分析及连接螺钉受力的大小或应力的大小等问题上，并没有进一步分析连接结构的受力规律，同时也很少分析不同形式连接结构间受力的差异。工程上常用连接结构的形式比较多样，本文主要针对减压阀双U形环连接结构、箍片及螺钉连接结构分别开展冲击动力学仿真分析。重点研究冲击环境下U形环、连接螺钉轴向力的变化规律，并通过研究连接件对减压阀的压力变化进一步分析出冲击环境下连接结构轴向力出现差异的力学机理。

1 分析模型及计算方法

1.1 分析模型

图1给出某型号减压阀固定连接结构的两种连接方式：①前、后U形环连接结构；②前U形环、箍片及螺钉连接结构。为提高计算效率，分析模型对减压阀局部几何特征进行简化，并忽略进、出气嘴等局部小结构。第一种连接模型主要包括减压阀、前U形环、后U形环、垫块及底座。其中，减压阀轴向总长度165 mm，大端直径69 mm，总质量1.7 kg。前、后U形环及螺钉直径均为5 mm。两种固定连接结构不同点对比见图2，即第二种连接方式是在第一种连接方式基础上把后U形环换成箍片与螺钉。

图2 两种固定连接件对比

基于ABAQUS有限元通用软件，建立完整的减压阀及其固定连接结构的有限元模型(见图1)。模型中各组件均采用体单元模拟，减压阀自身结构采用离散刚体模拟，其余结构采用变形体模拟。模型离散网格方面，对前、后U形环、箍片及螺钉等组件进行加密处理，模型总共包含103 256个节点及85 711个单元。各组件间的连接关系均采用硬接触模型及罚函数模型分别模拟法向、切向的相互关系，其中，罚函数模型中摩擦因数按经验给定0.04。U形环及连接螺钉处分别施加相应的预紧力，预紧力均为3 000 N。

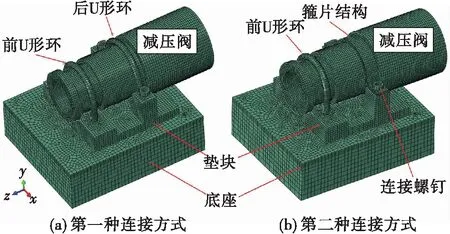
图1 减压阀两种连接结构

1.2 计算方法的考虑

在减压阀及其固定连接装置的冲击动力学响应分析中，由于连接件的受力主要表现为单向受拉，故在材料的塑性强化阶段采用等向强化模型就能满足模拟实际的要求。本文材料采用应变率无关的弹塑性模型，在材料屈服后该模型的应力应变关系是非线性的，与加载过程有关，分析过程中是通过给定屈服函数、强化模型和流动法则来确定增量形式的本构关系。

结构运动方程可表示为

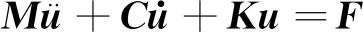
(1)

式中：、、分别为计算模型的质量阵、阻尼阵、刚度阵；为位移向量；为外力向量。

动力学仿真采用隐式的Hilber-Hughes-Taylor法，该方法属于Newmark积分法，在结构瞬态动力学计算中具有较广的适用范围，并且具有较高的计算精度。该方法的求解过程需要引入以下关于速度及位移的关系式

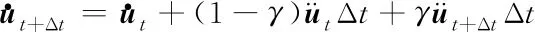
(2)

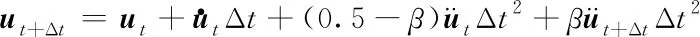
(3)

结合修正的运动方程

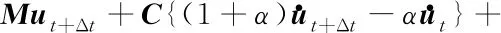
(4)

得到求解方程组

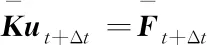
(5)

其中

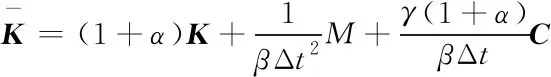
(6)

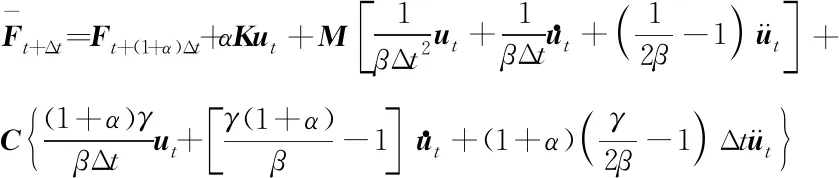
(7)

+(1+)Δ=(1+)+Δ-α

(8)

为保证计算具有无条件稳定性及二阶精度，、及的取值见表1。

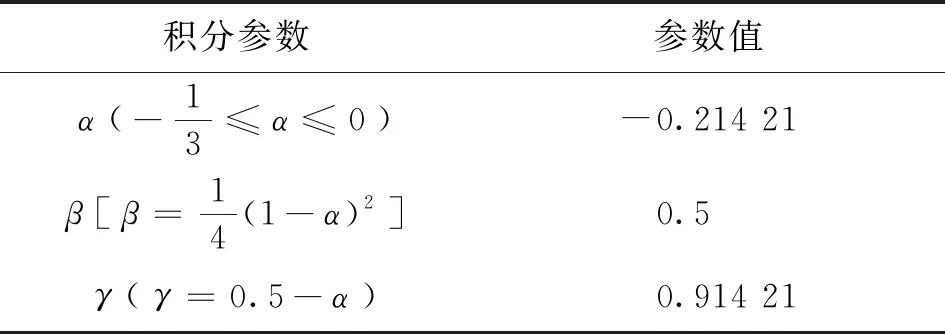
表1 Hilber-Hughes-Taylor积分法中的计算参数

另外，对于一般纯金属结构的冲击动力学响应分析，阻尼影响一般较小，在求解上述方程过程中可以不考虑阻尼带来的影响，即=0。

2 模型中材料参数

减压阀两种固定连接结构中前、后U形环、箍片及螺钉等组件的材料均为不锈钢1Cr18Ni9Ti，其余材料均为2A14，材料性能参数见表2。

表2 材料性能参数

3 冲击载荷条件及其加载

减压阀冲击载荷条件由多次实测数据统计包络得到，见表3。

表3 减压阀冲击载荷(Q=10)

激励载荷：计算中取减压阀底座下端面为仿真加载位置，取向作为激励加载方向。

约束边界：约束减压阀底座下端面除激励方向外其余方向的自由度。

开展冲击载荷下结构瞬态动力学计算，需要对表3的频域数据换算到时域，再进行时域的计算，换算后冲击载荷条件见图3，计算中时间长度为0.025 s。

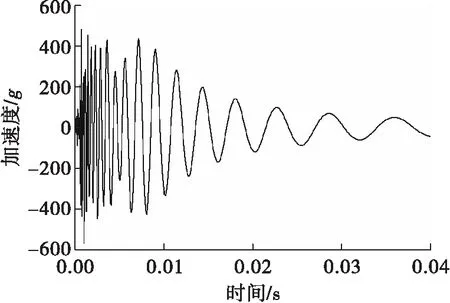
图3 冲击载荷条件时域数据

4 计算结果及分析

4.1 两种连接方式计算结果及其分析

计算得到冲击环境下减压阀两种固定连接结构中前、后U形环、连接螺钉最大轴向力的计算结果见表4，冲击过程中连接件(U形环、螺钉)轴向力变化曲线分别见图4和图5。

图4 冲击过程中第一种连接方式U形环轴向力变化曲线

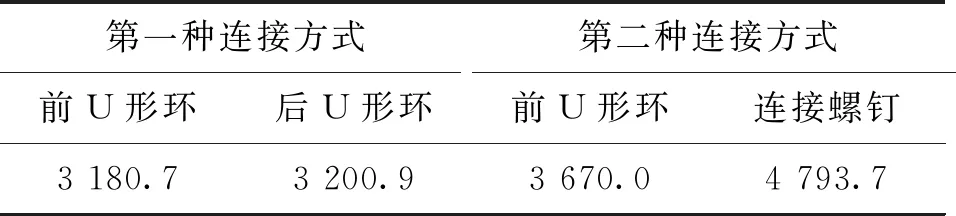
表4 冲击载荷下U形环、螺钉最大轴向力的计算结果

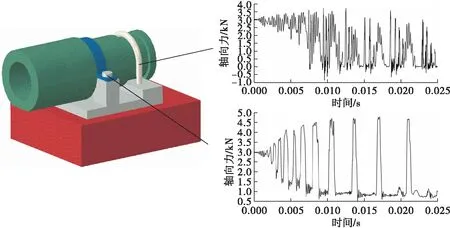
图5 冲击过程中第二种连接方式U形环、螺钉轴向力变化曲线

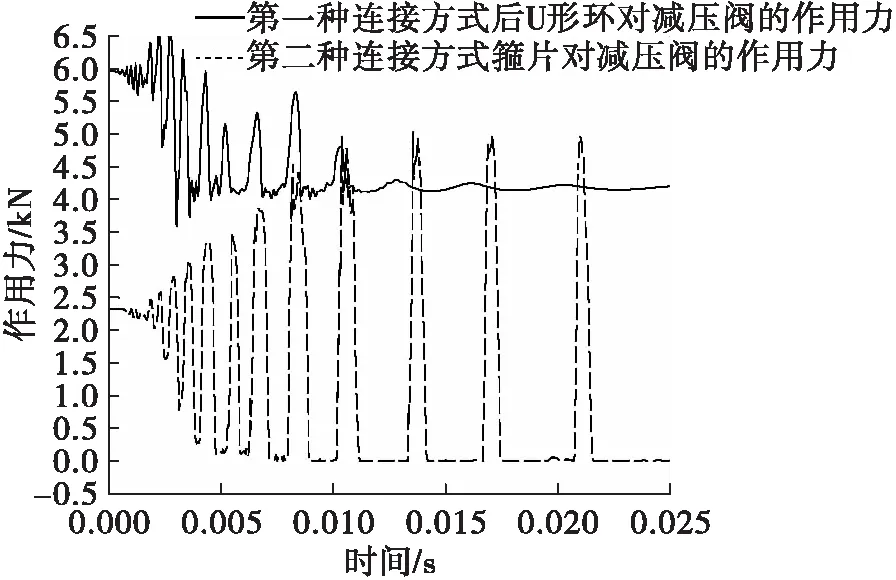
图6 冲击载荷下后U形环、箍片对减压阀的作用力变化曲线

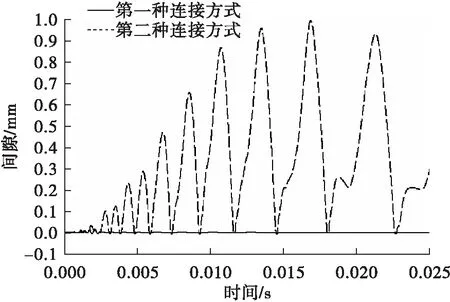
图7 冲击载荷下两种连接方式中减压阀与垫块间间隙变化

图6表示在冲击的初始时刻，后U形环、箍片对减压阀均具有一定的初始压力。其中，第一种连接方式后U形环对减压阀的压力约为6 kN，近似于后U形环预紧力之和，而箍片对减压阀的压力约为2.3 kN，远小于两螺钉预紧力之和6 kN，这一方面是由于螺钉发生了偏斜，另一方面是因为垫块抵消了很大一部分螺钉预紧载荷，见图8。

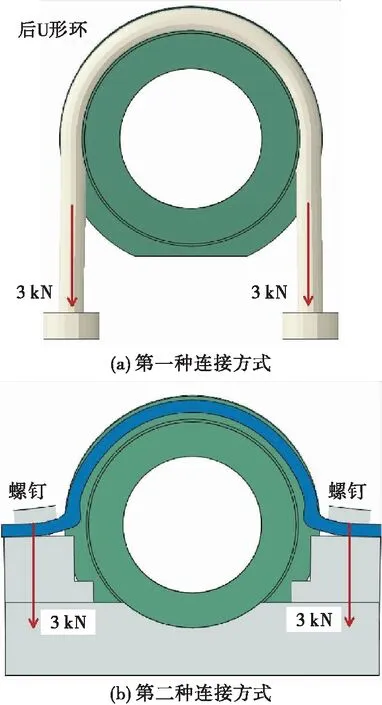
图8 预紧过程中两种连接方式的结构变形

另外，经历冲击载荷后两种连接方式中U形环、螺钉轴向剩余预紧力均存在不同程度的下降(初始预紧力均为3 kN)，具体见表5。

表5 冲击载荷下两种连接方式U形环、螺钉剩余预紧力

通过观察冲击载荷环境下连接结构的塑性应变数据，发现U形环、螺钉均出现明显的材料屈服，见图9。因此，可以看出：连接件(U形环、螺钉)在冲击环境下发生了材料屈服，其剩余预紧力会相应地下降。上述机理分析均在4.2节和4.3节通过相关验证模型进行仿真验证。

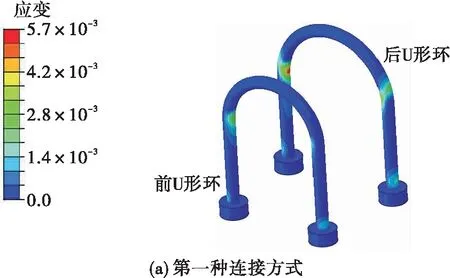
图9 冲击载荷下两种连接方式U形环、螺钉的塑性应变分布

4.2 轴向力变大的机理验证

为了验证连接结构轴向力变大的分析机理，对第二种连接方式的减压阀模型进行调整得到验证模型1。第二种连接方式模型的调整主要是保证冲击环境下箍片对减压阀能够在-向产生持续的作用力，因此，把原模型垫块中的支腿改成圆柱状，并在圆柱状支腿施加预紧力，保证螺钉的预紧拉力达到3 kN，见图10。

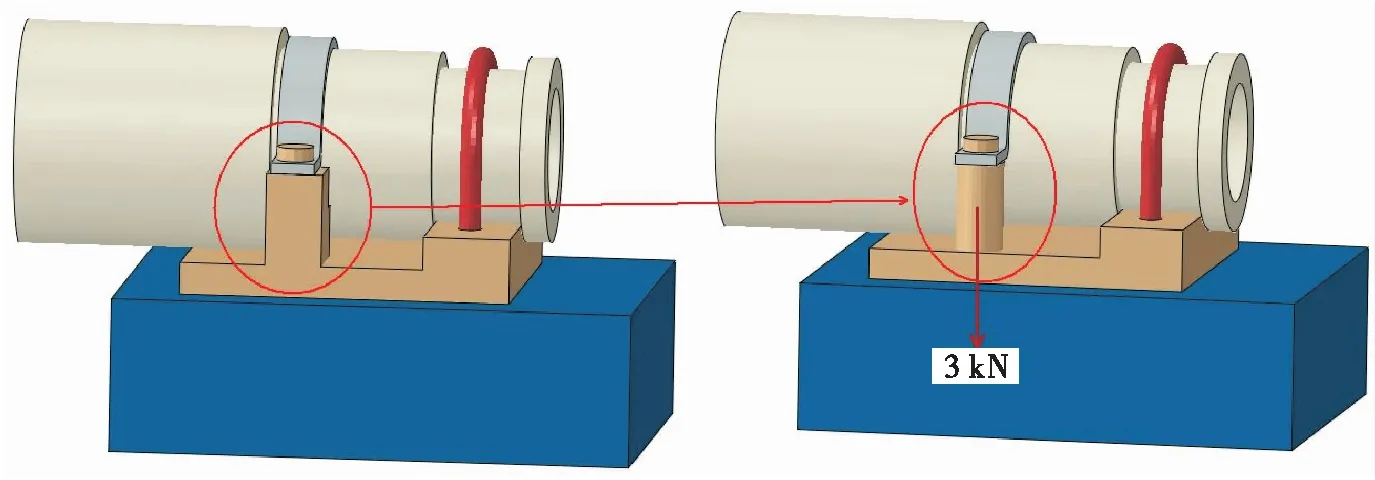
图10 第二种连接方式模型(左)及验证模型(右)

采用与之前同样的算法对验证模型1进行瞬态计算，得到冲击环境下验证模型1前U形环、连接螺钉最大轴向力的计算结果，见表6。

表6 冲击过程中验证模型1前U形环、螺钉最大轴向力的计算结果

从表6及图11可以看出，验证模型一前U形环、连接螺钉最大轴向力与原模型相比，有了明显下降，并且螺钉轴向力没有了阶段性地逐渐变大的现象；图12表明验证模型1在冲击过程中箍片对减压阀具有持续预紧力。这表明4.1节关于连接螺钉比第一种连接方式中后U形环轴向力大的机理分析是正确的。因此，固定连接结构在冲击环境下需要具备持续的预紧力，才能保证连接结构不会产生阶段性逐渐变大的轴向力。

图11 冲击过程中验证模型1前U形环、连接螺钉轴向力变化曲线

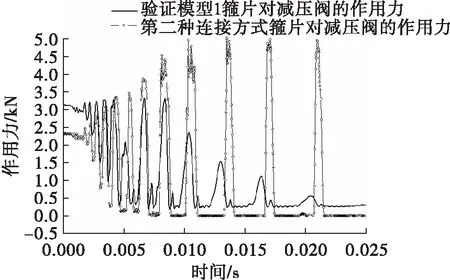
图12 冲击过程中验证模型1及其原模型箍片对减压阀的作用力变化曲线

4.3 剩余预紧力减小的机理验证

为了验证冲击过程中连接件剩余预紧力减小的机理，分别对第一种、第二种连接方式的减压阀模型进行调整得到验证模型2、验证模型3。模型的调整是为了冲击过程中连接件的材料不产生屈服，因此，只需要在第一种、第二种连接方式的减压阀模型中去掉连接件材料的塑性模型即可得到验证模型2、验证模型3。采用与之前同样的算法对验证模型2、验证模型3进行瞬态动力学计算，得到冲击环境下验证模型2、验证模型3中U形环、连接螺钉轴向力变化曲线，见图13和图14。

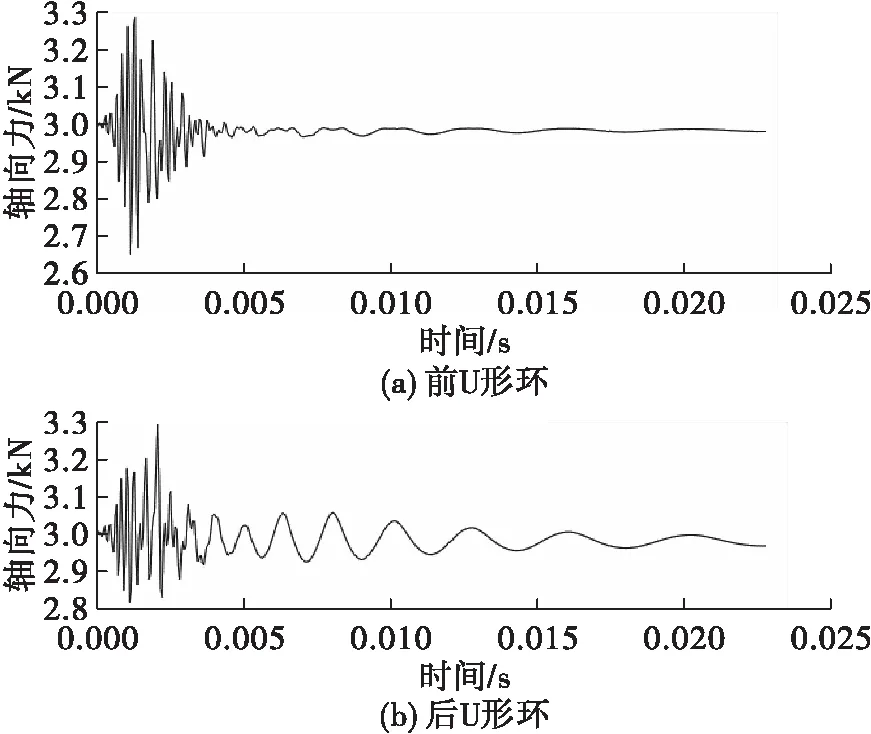
图13 冲击过程中验证模型2前、后U形环轴向力变化曲线

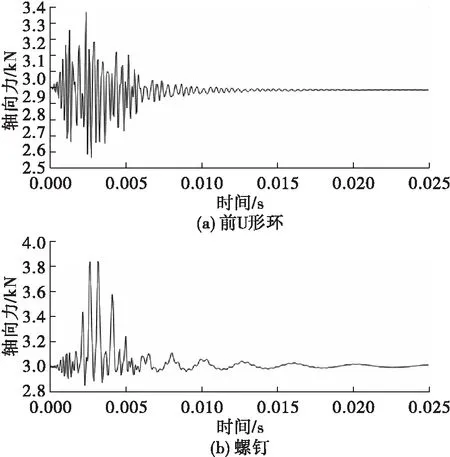
图14 冲击过程中验证模型3前U形环、螺钉轴向力变化曲线

图13、图14均表明：在冲击过程中连接件没有出现材料屈服，连接件的剩余预紧力也没有出现相应的下降现象。由此说明，关于连接件(U形环、螺钉)在冲击环境下剩余预紧力下降的机理分析是正确合理的。由于材料屈服产生的塑性应变往往比弹性预紧力产生的弹性应变要大，因此，冲击载荷环境下，连接件出现的材料屈服容易使得连接件预紧力下降至零，而当连接件没有了预紧力，则会造成连接件在冲击过程中出现阶段性逐渐变大的轴向力，从而引发连接松动甚至结构破坏的隐患。可见，若一个固定连接结构在某冲击环境下不产生塑性应变，那么该固定连接结构就能无限次或接近无限次安全承受给定的冲击环境。

5 结论

通过对减压阀固定连接结构的冲击动力学仿真分析研究，可以得到以下结论。

1)从低轴向力、轻量化这两方面来说，减压阀第一种固定连接方式(双U形环连接形式)均优于第二种固定连接方式。

2)固定连接结构在冲击环境下需要具有持续预紧力，才能保证连接结构不会产生阶段性逐渐变大的轴向力。

3)冲击过程中，连接件(U形环、螺钉)发生了材料屈服，会造成连接件剩余预紧力下降。

4)一个固定连接结构在给定冲击环境下可以无限次或接近无限次安全重复使用的充分条件是：冲击环境下该固定连接结构不产生塑性应变。