液体火箭发动机多层嵌套钎焊铣槽式换热器传热模型

2022-08-12刘军彦田雅洁杨永强霍世慧

火箭推进 2022年4期

刘军彦，王玫，田雅洁，杨永强，霍世慧

(西安航天动力研究所，陕西西安 710100)

0 引言

增压输送系统是液体火箭运载器的重要组成部分，也是大型液体火箭的关键技术之一。火箭飞行过程中需要对火箭贮箱进行增压，受推进剂输送要求及贮箱结构强度的限制，贮箱气枕的压力和温度必须维持在一定范围内，从而保证发动机涡轮泵的入口压力要求。大型火箭通常采用自生增压系统或贮存式惰性气体增压系统，而为了提高增压效率，节省增压介质，通常采用从发动机引出部分燃气对增压气体加热后再对贮箱进行增压，如中国“长征”系列火箭和俄罗斯、苏联的火箭大多采用加热后的氧化剂进行自生增压；欧洲“阿里安”火箭芯一级采用贮存式液氦加热增压方案；美国的“土星Ⅰ”、“土星Ⅴ”则采用自生增压+贮存式气体双增压方案。

加热增压气体的换热器结构型式一般为盘管式和多层嵌套钎焊铣槽式。与盘管式换热器相比，多层嵌套铣槽式换热器具有结构紧凑、体积小、换热面积大、传热效率高、可靠性高等优点,铣槽式钎焊结构在俄罗斯及国内火箭发动机推力室及高超声速飞行器机体等需要高效冷却的结构上也被广泛采用。

多层嵌套铣槽式换热器结构复杂，流道尺寸一般比较小，采用三维数值进行流固耦合传热计算时网格数量很大，计算周期长，不适合换热器的快速设计，因此本文在对多层嵌套铣槽换热特性及影响传热计算准确性因素分析基础上，建立了一维数学仿真模型并编写了传热计算程序，针对低温低压增压介质存在的两相流换热计算采用了简化计算方法。设计的换热器在火箭发动机上进行了搭载热试，根据试验数据修正后的传热计算模型适用范围更宽，准确性更高，可用于类似结构换热器的初步优化选型设计。

1 换热器设计参数

某液体火箭贮箱增压介质换热器设计参数如表1所示，增压介质为氧，燃气为富氧燃气。

表1 换热器设计参数

2 多层嵌套铣槽式换热器设计方案

换热器选用结构紧凑、换热效率高的多层嵌套钎焊铣槽式方案，图1为该类换热器的局部剖切示意图。

图1 多层嵌套钎焊铣槽式换热器局部剖切示意图

换热器由两个或多个组件嵌套在一起组成，其中增压介质换热组件由一个外壁铣槽的内圆筒和一个外壁上铣槽或不铣槽的外圆筒钎焊而成，夹层通道为增压介质通道，燃气在外圆筒的铣槽通道内流动，图1所示换热器最内层还带有燃气调节通道，用以组织燃气流动。根据换热器结构的不同，换热组件内部的增压介质通过壁面与外部燃气之间为双面或单面换热。

3 换热器计算模型

3.1 物理模型

以典型的换热组件双侧换热结构为例说明换热物理模型的选取。任取一个完整的增压介质换热通道(流道+两侧的半个筋宽)及内外两侧对应的燃气通道为换热微元截面，沿流动方向建立传热微元物理模型，见图2。换热器工作时，换热组件夹层中的增压介质与两侧燃气同时进行换热。

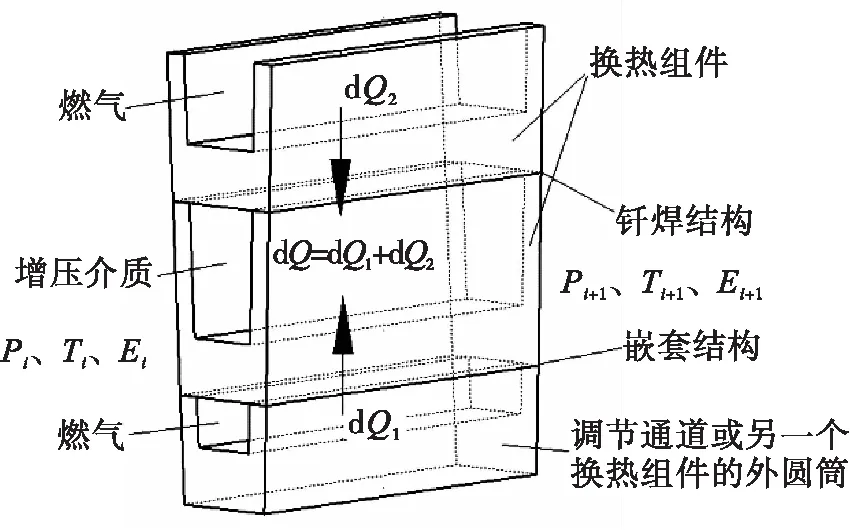
图2 换热微元物理模型

本文采用一维追赶法进行换热器的传热计算。从增压介质入口开始，按照给定步长，沿流向将换热通道划分成一个个换热微元。增压介质和燃气在换热微元吸热/放热后，换热计算由节点推进到节点+1，然后以节点+1的参数作为下一个传热微元的入口参数，依次下去，直至遍历整个换热通道，对于多层嵌套换热结构，增压介质和燃气都可能存在双向换热，因此必须经过多次遍历迭代才能保证传热计算的收敛。

圆筒外壁肋选用了有精确传热解析解的矩形肋，以保证传热计算的准确性。通过对多层嵌套式钎焊铣槽结构换热器结构传热特点进行分析后发现，对传热计算准确性有影响的主要因素如下。

1)夹层肋高在双侧换热计算时的分配：对于双面换热的换热组件夹层肋筋而言，夹层肋的温度从两侧肋根向中间是逐渐降低的，则必然有一个最低温度面，这个温度面两侧的肋高就是计算夹层内流体与外侧燃气换热时的强化换热肋高，而且这个最低温度面所处肋高在相邻换热微元是变化的，即温度面所处高度沿通道是不断变化的。

2)换热组件内侧换热面积的修正：换热组件与内侧调节通道或另一个换热组件之间为嵌套配合结构，两者之间实际上处于一种局部点、线、面接触状态，所以换热组件内侧光滑壁面的实际换热面积会因遮挡而减小。

3)换热微元外侧肋效率的计算：换热微元以一个完整的增压介质通道为基准，在计算换热组件外侧肋的肋效率时，由于内、外肋数量并不一定相同，因此必须将外侧的肋效率按照一定的规则折算到基准换热面上。

进行传热计算时作以下简化和假设：

1)无论是结构上还是流体中，沿流动方向或轴向无热传递；

2)不考虑热损失；

3)如增压介质在换热过程中存在两相流换热，则采用简化模型计算两相流的对流换热系数(具体见后文)；

4)流体物性按照变物性考虑，但在换热微元内是常量；

5)冷热流体之间的换热温差取流体的静温差。

3.2 数学模型

在稳态换热情况下，根据热平衡可知，单侧燃气向增压介质的热量传递经历3个过程：燃气与壁面的对流换热、热量在固体壁面的导热及增压介质与壁面的对流换热。稳态换热时，3个过程的换热量是相等的，即

(1)

3个过程的换热量可依据式(2)进行计算。

=(-)

(2)

式中：为3个传热过程对应的换热系数；为换热面积；、分别为流体、壁面的温度。

3.2.1 氧侧和燃气侧的对流换热

增压介质和燃气在铣槽通道内的流动可看作是管内强迫流动，其对流换热系数可采用目前广泛使用的Sieder-Tate关联式进行计算，即

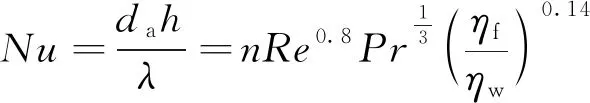
(3)

式中：流体定性温度为平均温度；为努塞尔数；为对流换热系数；为流体的导热系数；为换热通道当量直径；为由试验数据确定的常数，取0.027；为流体雷诺数；为流体普朗特数；为流体的动力黏度；为平均壁温对应的流体动力黏度。适用范围：≥60，=06～16 700，≥10。

当以液氧等低温液态工质作为增压介质且对其在亚临界状态进行加热时，则会存在两相流换热，液态增压介质吸热汽化，温度不变，但其焓值是不断增加的。

两相流换热区对流换热系数的大小与流型关系密切，而流型又受流体压力、流速、传热温差、流道方位(水平或垂直)、环境振动等因素的影响。文献[17]根据数值模拟得到计算的拟合公式形如式(3)，其取0.04，的指数取0.5，而文献[12，18-19]则给出了更为复杂的计算公式。可见两相流对流换热系数计算根据相似准则选取的不同，准则方程式具有多样化，而且每个准则方程式的适用范围有限、条件苛刻。鉴于两相流换热只发生在局部区域，换热量占比相对较小，本文将采用简化模型计算两相流换热区的对流换热系数，即仍然采用式(3)计算两相流的对流换热系数，但相关流体参数用氧在两相流换热时干度和饱和液态、气态的数据插值计算得到，具体方法为：在进入每一个传热微元前，根据流体压力和焓值判断流体是否处于两相流态，若是，则计算入口压力对应的饱和液态与饱和气态点的物性参数，如焓值、密度、动力黏性等，根据入口焓值及饱和态的物性数据可线性插值得到当前计算传热微元内的流体物性参数，最后将这些参数代入式(3)计算得到两相流的对流换热系数。

3.2.2 壁面的导热

相对于铣槽圆筒的直径尺寸，各换热微元的截面尺寸为小量，因此通过圆筒壁面的导热可简化为铣槽平板近似考虑。通过壁面的导热量计算公式为

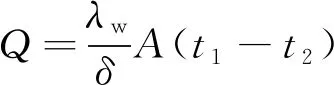
(4)

式中：为圆筒壁厚度；为换热面面积；为壁面平均导热系数。

图3为直肋铣槽结构示意图。肋总效率计算公式为

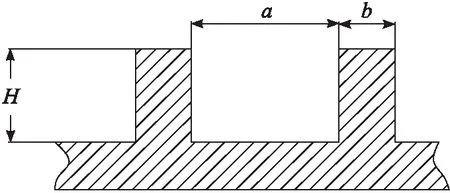
图3 带肋换热通道结构简图

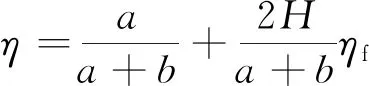
(5)

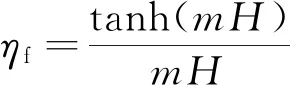
(6)

(7)

式中：为槽宽；为肋宽；为肋高；为肋效率。

3.2.3 总传热系数

换热微元两侧换热需要单独计算，但换热微元出口的物性要根据双侧换热进行计算，传热计算取圆筒壁中间层面积为基准换热面，燃气与增压介质总换热系数计算公式为

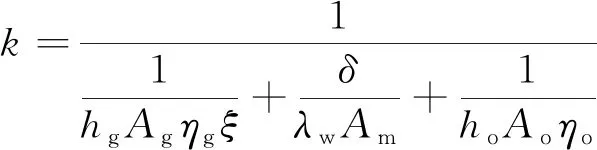
(8)

式中：为外侧肋效率的折算系数；下标g代表燃气侧参数，m代表基准面参数，o代表氧侧参数。

3.2.4 流体压降的计算

气体在换热微元内的压降计算公式为

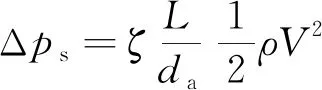
(9)

式中：为沿程流阻系数；为换热微元长度；为流通截面的当量直径；为流体密度；为流动速度。

当<10时，可按式(10)计算

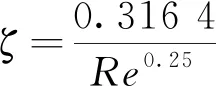
(10)

当10≤≤10时，可按式(11)计算

(11)

式中为换热通道壁的表面粗糙度，对机加流道，取0.015比较合适。

燃气和增压介质在换热通道两端的流阻系数可查阅流体阻力手册计算得到，然后采用式(12)计算。

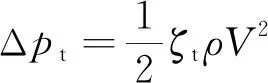
(12)

当铣槽通道为螺旋槽时，由于离心力作用而产生的所谓“二次环流”会拉薄附面层强化对流换热，螺旋槽中的对流换热系数可以在直槽对流换热系数的基础上乘以修正系数。对于螺旋槽，修正系数可表示为

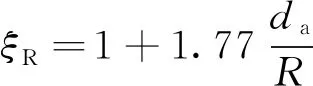
(13)

式中为螺旋槽的螺旋半径。

4 传热计算结果与试验结果的对比

4.1 结构尺寸设计计算

根据表1换热器设计参数及上文所述的传热模型完成了换热器设计，换热器流动布局如图4所示，换热器各圆筒壁厚度按照结构强度要求取值，各通道轴向长度315 mm，其余结构参数见表2。B/C、D/E通道材质为铜外，其他结构材质全部是钢。

图4 液氧换热器的流动布局

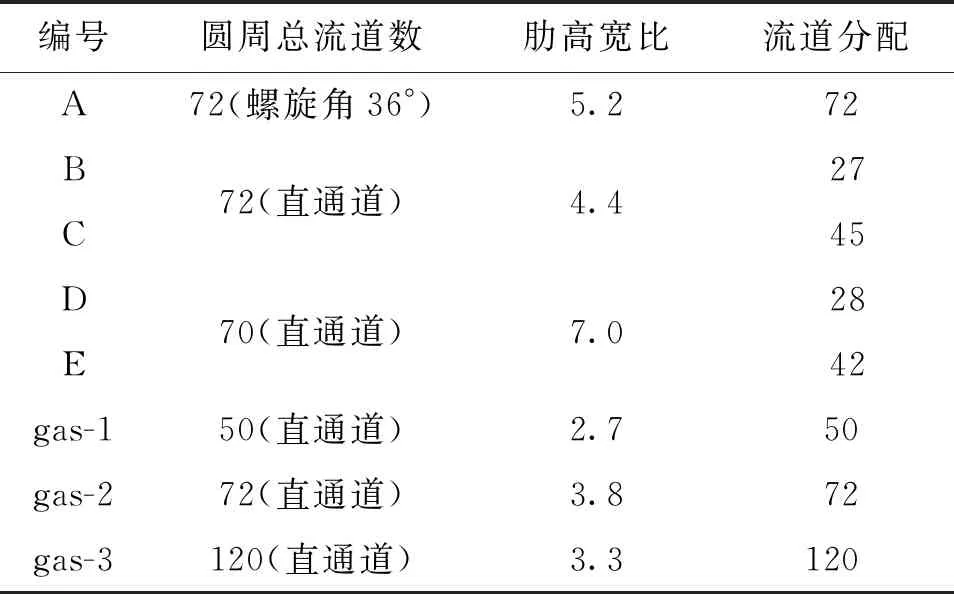
表2 换热器结构参数

换热器由调节通道、换热组件1、换热组件2、换热组件3及换热器两端的导流结构等组成。

燃气从换热器一端中心引入，经S形通道与3个换热组件进行换热，最后从另一端中心引出；增压介质从燃气出口端沿换热器外壳体径向引入，依次流经A、B、C、D、E通道后从另一端沿径向引出。换热组件1为单向流道，换热组件2和3为往复流道。可以看出，增压介质在换热组件1内为单侧换热，在换热组件2和3内为双侧换热；燃气在gas-1通道内为单向换热，在gas-2和gas-3通道为双向换热。燃气与增压介质之间为顺、逆“混合流动”换热。

4.2 传热计算结果与试验结果的对比

通过试算，传热微元长度取5 mm可满足计算精度要求(换热微元长度取值越小，计算越精确但计算所需时间越长)，各换热层沿轴向可分为63个传热微元，燃气入口端传热微元编号为1，末端编号为63。

4.2.1 换热器传热计算

首先进行了设计参数下的传热计算。图5为各换热通道中微元节点处的温度曲线。低于超临界压力(5.043 MPa)的液氧在换热时会出现温度不变、焓值增大的两相流换热区，在图5中表现为A、B通道内有一段温度重合区。未饱和液氧进入A通道后温度缓慢升高，经过长约115 mm通道的加热后成为饱和态液氧，随后进入两相流换热态，在A通道末端时，依然为两相流状态，进入B通道再经过约85 mm长度的换热后最终变成饱和气态，在这个过程中氧的温度始终保持恒定值141.7 K(实际上因为氧沿程流动有压降，其各节点饱和温度有微小变化)。

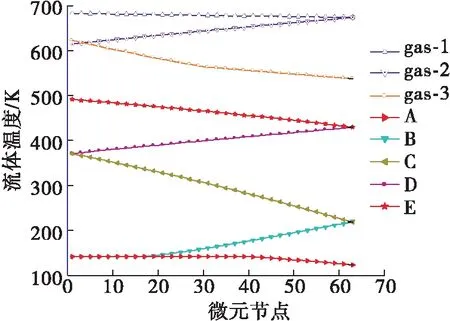
图5 各换热通道中流体温度的变化

由于传热计算采用了实验关联式，必然带来一定的不准确性，因此换热器设计时一般要留有一定的裕量。本文设计的换热器在设计参数下的氧出口温度为487 K，满足设计要求，当热试温度高于要求值时，可通过调整参与换热的燃气流量对氧的出口温度进行调节。

图6为各换热通道中传热微元节点的对流换热系数。与图5对比分析，在A通道内，液氧进入两相流换热前，其对流换热系数缓慢增大，在进入两相流换热后有一个突降；同样现象也出现在B通道两相流换热结束时，表现为对流换热系数有一个突升。分析认为，这两个突跃主要与液氧、气氧在饱和态附近物性变化剧烈有关，由于计算微元长度取值相对较大，所以未能捕捉到气、液饱和态对流换热系数的极大值，其高点被“削平”。在远离饱和态的区域，除在换热器两端流向及流道参数变化引起的对流换热系数变化外，各流道中的对流换热系数变化都是很平缓的。从图6还可以看出，各通道内的对流换热系数相差比较大，这与换热流通面积、流体物态及物性等诸多因素有关。比如在B通道的两相流换热段，该处流体物性虽然与A通道两相流换热段的物性基本相同，但由于B通道的流通面积小，所以两相流对流换热系数值要大很多；在B通道的后半段，气态氧的对流换热系数却与A通道初始换热段内的液氧对流换热系数相近。

图6 各换热通道中对流换热系数的变化

图7为换热组件2夹层B通道肋的等温面距内侧换热壁的高度(无量纲)及该等温面的温度沿计算节点的变化。

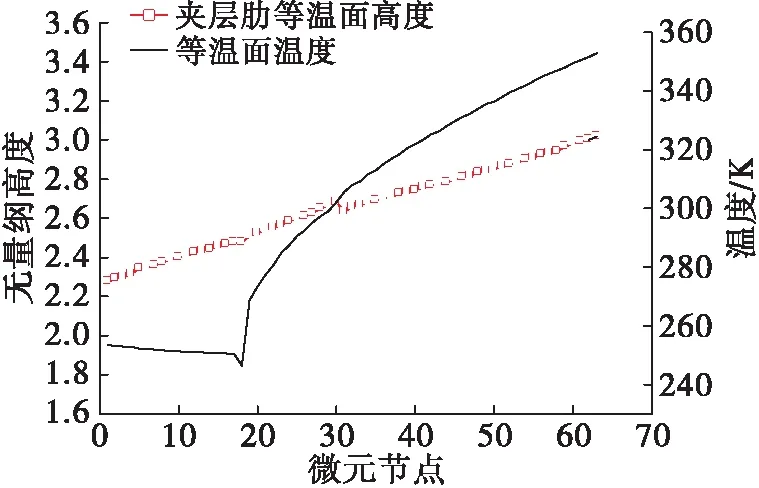
图7 等温面高度及温度沿程变化

从图中可以看出，在开始的一段距离内，由于液氧为两相流换热，氧的温度是不变的，但肋的等温面并不在肋中间,而是偏向换热组件外侧。增压介质在B通道换热进入纯气态换热后，肋等温面所处高度和温度开始明显增大，表明换热组件2与内侧燃气的换热要强于外侧换热，这主要是因为换热组件2内圆筒壁采用了比外圆筒壁具有更高导热系数铜材的缘故，即使被换热组件1外侧肋所遮挡，内壁材质的导热特性依然将夹层肋的等温面推向外侧。

此外，在图7中出现一个奇怪的现象，即在第30号节点处的等温面位置突然降低，然后又掉头向上，通过与图5和图6进行对比，B通道内氧及两侧燃气的温度、对流换热系数并没有出现突变。分析影响换热和等温面高度所有因素后发现：3 MPa的液氧吸热完全汽化后温度升高时，除了导热系数具有先降后升这一特点外(见图8)，其他物性都是单调增加或降低的，而且导热系数极小点对应的温度恰好就是30号节点B通道内气氧的温度。分析认为，氧导热系数发生趋势变化对增压介质侧的对流换热系数产生影响，而内圆筒壁材质由于导热系数大，传热热阻小，换热组件内圆筒夹层侧壁温(肋根温度)对增压介质对流换热系数的变化更为敏感。等温面高度突变虽然对换热结果影响有限，但其机理值得后期做进一步研究。

图8 气氧导热系数随温度的变化

4.2.2 传热计算与试验结果对比

设计的换热器在地面研制发动机上进行了多次搭载热试。试验测量参数有：燃气、增压介质在换热器进、出口处的压力和温度。燃气和增压介质流量通过相关测量参数计算得到。本文随机选取6次热试结果进行分析，其中，试验1～试验3的增压介质为液氧，试验4～试验6的增压介质为常温氮气。

图9为各次试验的流量图。图10为换热器出口换热介质计算温度与试验温度的对比图，图11为换热器出口换热介质计算压力与试验压力的对比图。

图9 各次试验下的流量

图10 计算温度与试验温度的对比

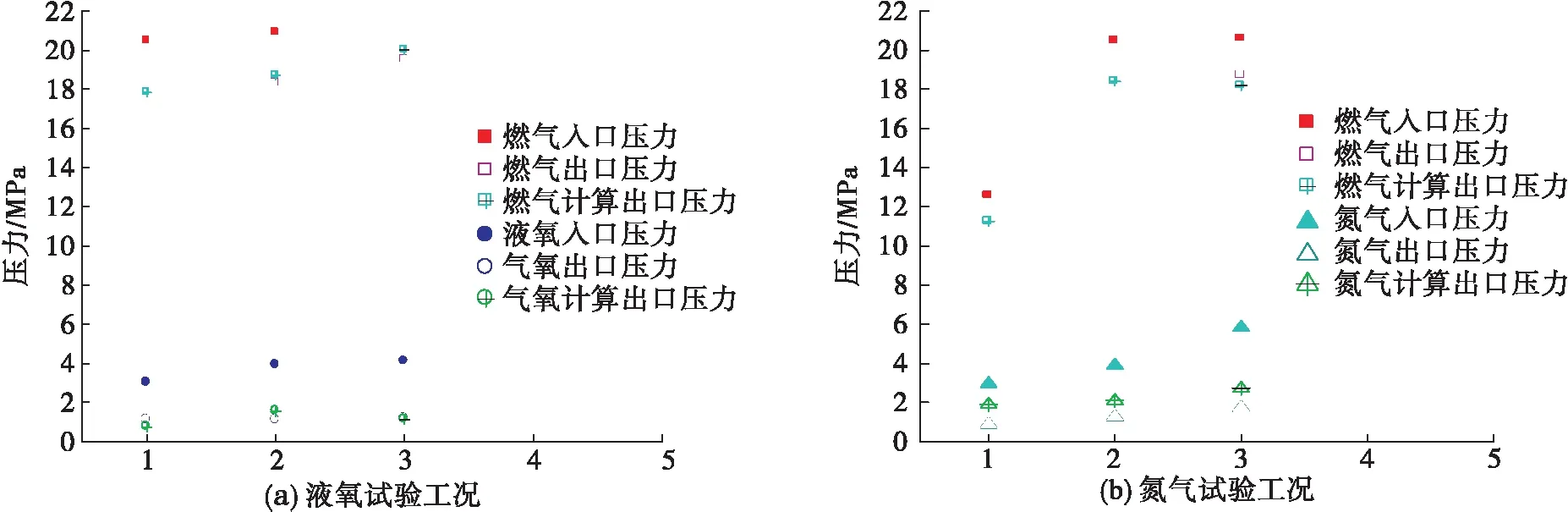
图11 计算压力与试验压力的对比

从图11压力图可以看出，燃气在换热通道出口处的计算值与试验测量结果不一致，当增压介质为液氧时，其在换热通道E末端的压力与试验测量值基本相当，最大误差绝对值为0.35 MPa；增压介质为氮气时，最大误差绝对值为1.0 MPa左右，燃气计算最大误差绝对值为0.52 MPa。除试验测量误差外，计算误差主要来自于3个方面：一是计算的出口压力在流道E的末端，而试验测量点在换热器外；二是流阻系数，特别是换热通道两端流阻系数根据流阻手册进行估算得来，误差不可避免；三是两相流换热区压降采用简化计算方法，也会带来一定误差。

为了分析压力对换热的影响，通过人为改变计算程序中增压介质在换热通道两端的流阻系数，使增压介质在换热通道E出口处的计算压力尽量接近试验测量结果，计算结果表明：压力改变对增压介质出口温度影响很小，最大温差值在3 K左右。分析认为，压力之所以对气体的换热影响很小主要是因为压力对影响气体换热的两个重要参数即气体密度和流速的作用是相反的：压力减小，气体密度减小，流速增大，反之亦然，反映在传热计算公式(3)上，则表现为压力变化时增压气体在通道中的对换热系数基本不受影响，气体出口温度基本不变。

4.2.3 换热系数的修正

对比出口温度可以看出，氮气的传热计算结果与试验结果更为吻合，液氧计算结果误差偏大的原因可能与建立传热计算模型时，为了规避液氧两相流换热的复杂性，采用简化计算模型有关，为了提高传热计算的准确性，借鉴工程上常用做法，对两相流区对流换热系数进行修正。根据试验结果，两相区的对流换热系数修正系数取0.89可以得到比较准确的计算结果。