燃烧组件时域分布参数系统动力学模型

2022-08-12李元启赵晓慧陈宏玉刘红军

火箭推进 2022年4期

李元启，赵晓慧，陈宏玉，刘红军，刘上

(1.西安航天动力研究所，陕西西安 710100； 2.西北工业大学航天学院，陕西西安 710072)

0 引言

燃烧组件是液体火箭发动机中重要的核心组件之一，其工作过程包含了流动与燃烧现象中极其复杂的物理化学过程，且工作参数在短时间内变化剧烈。对燃烧室工作过程的建模一直是学者重点研究的方向。特别是在发动机系统动态过程仿真中，既要考虑模型的准确性，又要保证一定的计算速度，使得燃烧室的建模工作极富挑战性。

早期的研究中，主要关心系统的低频缓变过程，燃烧室建模采用零维模型，该类模型反映的是参数的平均效应，能够在低频范围内描述燃烧室的建压过程。刘昆、程谋森等在此基础上将燃烧室分为燃烧区和流动区，燃烧区采用零维集总参数模型，对流动区和喷管建立一维理想气体假设下的流动有限元状态变量模型。刘上等利用线性化频域法建立了包含零维燃烧区和考虑声学效应的分布参数流动区的燃烧室模型，分析了涵盖燃烧室中高频的动态特性。上述分区模型将燃烧室动态特性的研究范围从低频扩充到了中高频率，但是其流动过程均采用了无源等熵流动的假设，与实际情况存在一定的差别。文献[9-11]在冲压发动机燃烧室性能分析时用一维欧拉方程描述燃烧流动过程，可以准确地反映燃烧室内的参数分布情况，但其模型中放热源项采用燃料热值与燃料流量的乘积来确定，仅适用于燃料完全反应的富氧工况。火箭发动机燃烧室内存在富燃或富氧的不同工况，该模型并不完全适用。

本文在前人基础上，基于一维气相欧拉方程，考虑液体推进剂蒸发加质、化学反应放热、流动截面积变化，建立了适用于火箭发动机燃烧组件系统动力学仿真模型。

1 数学模型与求解

假设燃烧室截面积是缓慢变化的，其参数的均值仅取决于一个方向的空间坐标和时间，则燃烧室内的物理过程可视为准一维流动和化学反应，在气相控制方程基础上考虑横截面积变化、物质质量添加、化学反应放热、壁面摩擦和变比热比等各种影响因素，则燃烧室内的过程可用准一维欧拉方程描述，其中向量方程的3个分量分别代表了质量守恒、动量守恒和能量守恒方程。

(1)

式中：为守恒变量；为通量函数；为源项。其表达式分别为

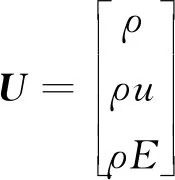
(2)

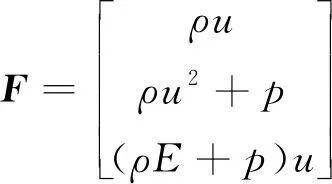
(3)

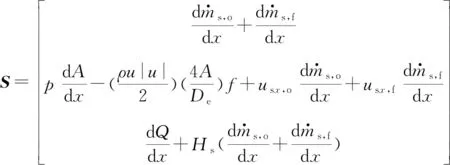
(4)

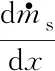
(5)

1.1 源项的分析

控制方程中较为关键的一项即源项，源项中包含了质量守恒方程的源项、动量守恒方程的源项和能量守恒方程的源项。其中质量守恒方程的源项代表液态推进剂蒸发成气态，从而给气相控制方程带来的加质项。其数学模型可以用蒸发和掺混的子模型来描述。动量守恒方程的源项代表了气体与壁面的摩擦损失。能量守恒方程的源项代表了气相推进剂之间化学反应的放热项以及气体与壁面热交换带来的加热或放热项。如何通过各个子模型准确地描述上述物理过程是燃烧室数学建模的关键。

加质项可表示为

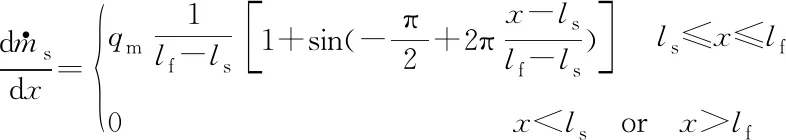
(6)

其物理意义为假设液态推进剂的蒸发沿燃烧室的分布形态为正弦信号的前半个周期，并且蒸发的范围限定于区间[，]内，式(6)满足，即保证了质量添加的守恒性

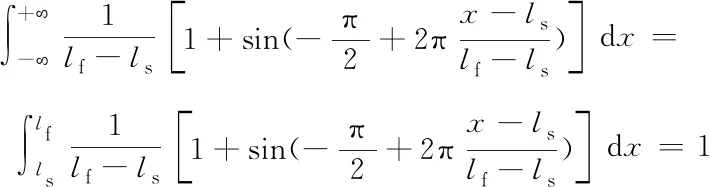
(7)

释热项主要是求反应焓的问题，通过热力计算可以得到推进剂化学反应的平衡温度，即

=(,)

(8)

式中：为混合比；为燃烧室压力。因此反应焓可以表示为

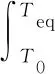
(9)

值得注意的是，混合比以入口的氧化剂和燃料的质量流量的比值来表示[见式(10)]，而不是以燃烧室内总的氧化剂和燃料的质量积存量来表示，因此燃烧室的热力参数可以敏感地对入口流量的波动进行响应。这样就解决了一大关键问题，即流量的高频扰动可以实时地被模型所反映，进而反馈到燃烧室的其他热力参数的计算上。故而该模型能够本质地适应高频相应的计算。

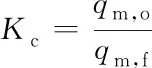
(10)

1.2 数值计算格式

空间离散采用了ROE格式，具体格式见文献[16]。由于存在源项和动量方程中面积变化带来的附加项，直接采用ROE格式计算会导致在面积变化处产生流量不守恒的现象，需对式(1)的特征向量进行修正，具体形式为

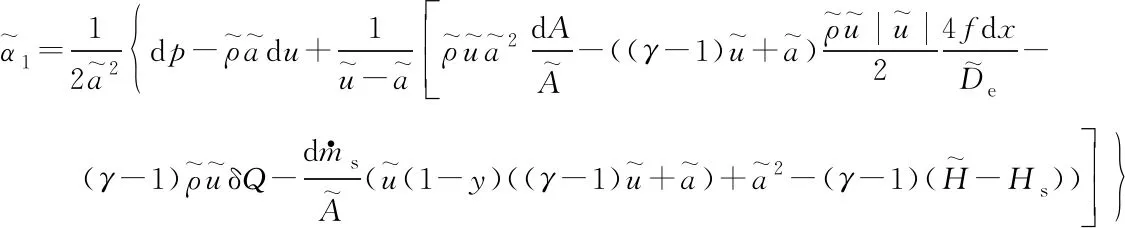
(11)

(12)

(13)

式中符号的含义见文献[16-17]。

对于火箭发动机而言，燃烧室内蒸发和化学反应的时间尺度非常小，而流动和传热的时间尺度较大，即意味着其数学模型存在很大的刚性，显式的欧拉法或龙格-库塔法求解刚性微分方程较为困难，因此时间离散采用了隐式变步长的时间推进Dassl方法。

2 算例验证

2.1 静态算例

以线性分布热源的问题为例，模型示意图如图1所示。气体工质为空气。流通通道为等截面，忽略气体的摩擦力，对于理想无黏流动，初始时刻加热量为零，则各个截面上气流参数相同，入口静压=1×10Pa，静温=300 K，单位横截面积上的气流流量=01 kg/s，管道总长度=0.1 m，管道截面积=001 m，气流通道内的热源分布为

图1 线性热源问题示意图

(14)

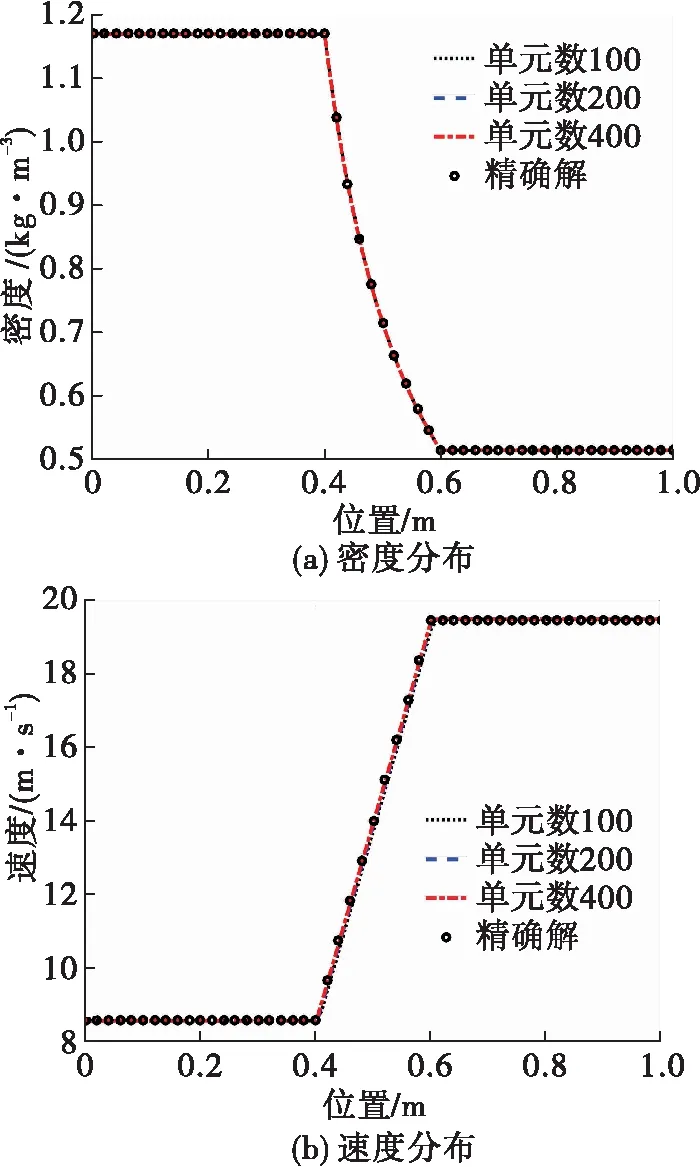
图2 线性热源问题计算结果

2.2 动态算例

以文献[20]中的试验结果为例，对含熵波和声波的气路算例的求解进行验证。如图3所示，该试验装置是由一段长约1.5 m和直径0.12 m的圆柱形流动管路组成，流路出口设置短喷管使流动达到临界音速，冷空气和热空气经过临界气喷嘴送入该试验装置流路。冷空气流路喷嘴前设置谐波干扰，使冷空气产生流量振荡，进而引起掺混气体的温度变化，以形成熵波，增大冷空气的流量会导致混合气温度降低，因此将冷空气等效为燃料，热空气等效为氧化剂。该方案可等效于富燃燃烧室，可以模拟富燃燃气发生器燃料流路中的干扰。高低温气体在头部处通过很多气喷嘴直接进行掺混，混合距离可以忽略不计，认为在燃烧室入口处已经完成了混合。

图3 试验装置示意图

给定入口边界条件，热空气温度=780 K，流量=684 kg/s，冷空气温度=300 K，流量为周期性变化，表达式为

=+Δsin(2π)

(15)

式中,c0=10 kg/s。

分别采用集中参数模型和本文的分布参数模型对该试验装置的动态特性进行仿真计算，并将时域解变换至频域，结果如图4所示，结果表明，在=0～600 s的低频范围内，气路的幅值响应有逐渐降低的趋势，即对低频幅值响应更敏感，相位差滞后随频率的增加有增加的趋势，在100 s以上的频率范围，在幅值和相位特性上均产生了熵波响应。

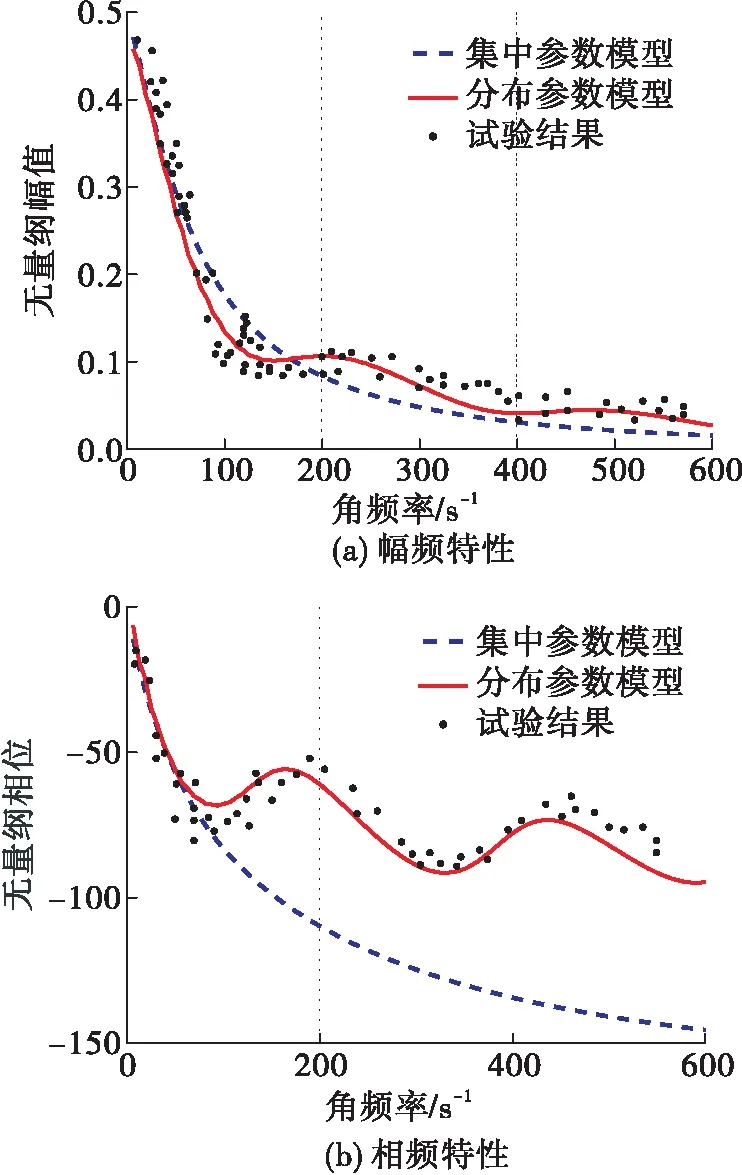
图4 试验装置末端的频率特性

从幅值上看，本文的分布参数模型和集中参数模型均和试验结果吻合较好，区别在于，集中参数模型不能捕捉到100 s以上的熵波现象，而分布参数模型完全能够反映出熵波现象。再从相位上看，集中参数模型在大于100 s的范围内，完全和试验结果相背离，而分布参数模型与试验结果能够吻合，再次验证了集中参数模型只能适用于低频范围内，=100 s对应的频率为100/2π，即不到20 Hz。这与文献中提到的频率范围相一致。而本文提出的分布参数模型所适用的频率范围远大于集中参数模型。

进一步地，将研究的频率范围扩充至中高频范围，取无量纲角频率0<<8，计算气路的频率特性，并与试验数据比较，图5为气路试验系统管路末端的压力频率响应特性，图6为气路试验系统管路中点位置的压力频率响应特性。

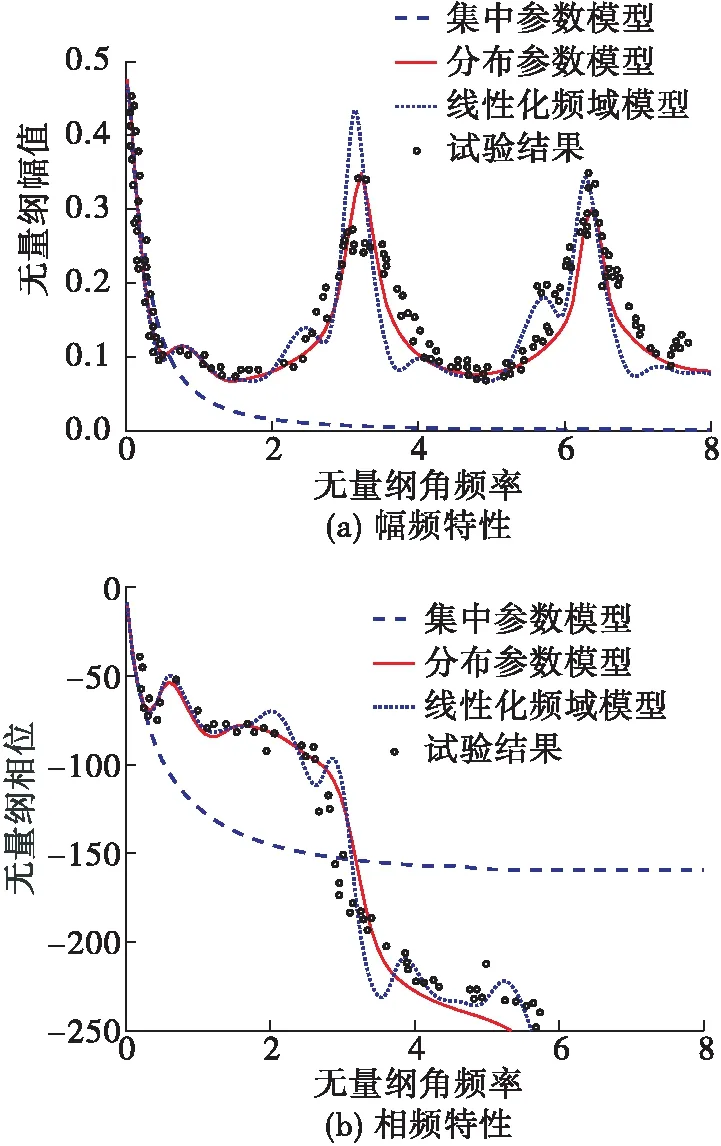
图5 气路试验系统管路末端压力频率响应特性

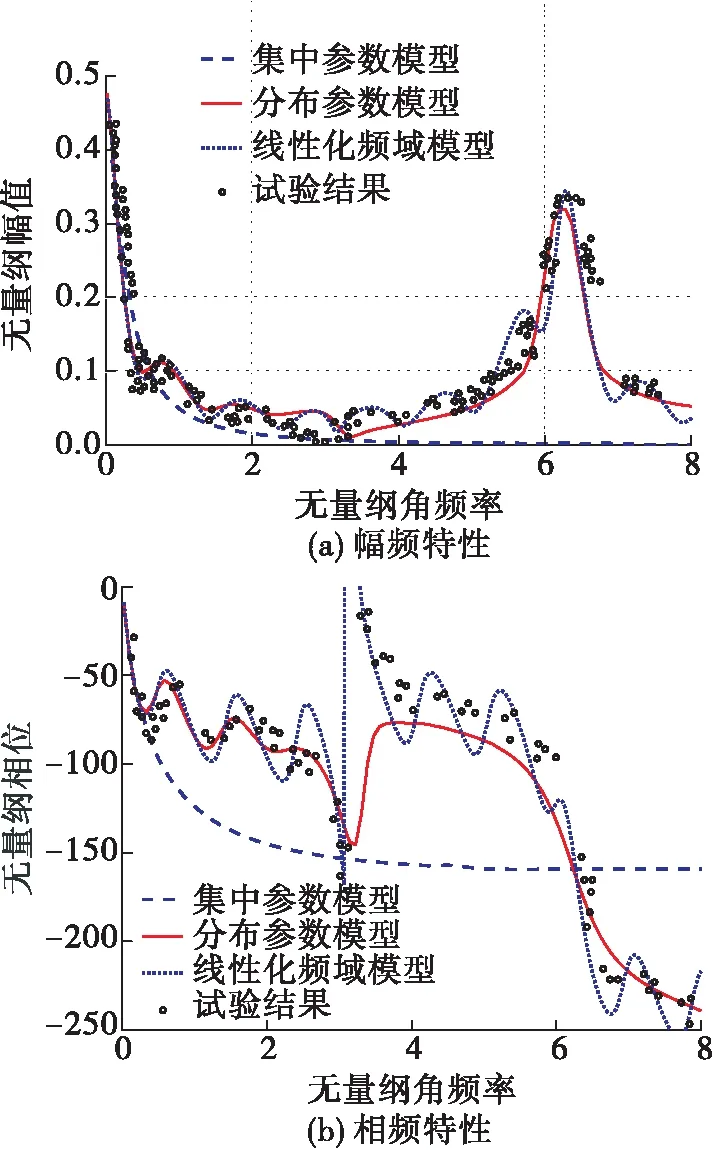
图6 气路试验系统管路中点压力频率响应特性

结果表明，在更高的频率范围内，采用集中参数模型计算的压力响应幅值趋向于0，说明了集中参数模型无法反映高频的响应特性。而分布参数模型和试验结果吻合较好，特别是在=π的位置，即一阶纵向声学频率处，气路的末端应处于压力振荡的波腹位置，振幅最大，气路中点处应处于压力振荡的波节位置，振幅最小。本文的模型准确地捕捉到了气路末端的压力响应峰和气路中间的压力波节，峰值和频率均与试验结果吻合。甚至到了二阶声学频率处(=2π位置)，该模型也有较好的计算结果，二阶声学频率下气路的末端和中点均为压力振荡的波腹，振幅最大，模型的计算结果和试验结果也能够吻合。从相频特性曲线上看，当入口流量的扰动频率增加时，气路中点和末端与入口的相位角滞后是逐渐增大的，相对而言，气路末端的相位角滞后相对更大，可以看到，分布参数模型对相位角的计算与试验结果也能较好吻合。

在低频范围内试验数据表明了气路中存在明显的熵波波动特征。但在无量纲角频率>1.5后，试验数据沿着比较平滑的曲线移动，这一点在相频曲线中体现得更加明显。这是由于熵波是一种物质波，其传播速度等于流速，文献[20]提到，在通常湍流度水平的圆柱形流路中，当频率大于400 Hz时，熵波会产生耗散效应。原因在于，熵波的产生机理是：当入口推进剂流量产生波动时，在燃烧室内会周期性地生成温度不同的燃气团，当扰动频率较低时，前一时刻生成的燃气团有足够的时间向下游流动，后一时刻在燃烧室头部生成新的燃气团时，前一时刻的燃气团已经流向了下游，各个温度不同的燃气团存在位置空间上的分布，气团随流体整体向下游流动，从而造成了燃烧室内的压力波动。当入口扰动频率很高时，上一个时刻生成的燃气团还没来得及流动到下游，又在同一个位置生成了另一个燃气团，高低温的燃气团几乎在同一位置生成，进而迅速达到热平衡，使得燃气温度在空间分布趋于平均效应，因此无法形成压力波动。在表象上熵波表现出了高频耗散效应，即在低频下，燃烧室的压力响应曲线上会叠加熵波响应，而在高频下，压力响应曲线不会叠加熵波响应，压力幅频响应曲线应趋于平滑。

与文献[8]中的燃烧室线性化频域模型相比较，见图5和图6。线性化频域模型在高频下仍存在叠加的熵波，在相频特性曲线上尤为明显，与上述物理过程不相符合。而本文所建立的时域非线性分布参数模型计算得到的响应曲线在低频处存在熵波叠加，在高频处趋于平滑，能够准确地捕捉到高频下的熵波耗散现象。原因在于，在时域的控制方程中，已经考虑了速度、压力和温度等参数之间的耦合关系，其传播和耗散特性已经在方程中得以体现。因此，只要差分方程和微分方程满足相容性关系，数值积分计算的结果就能够反映原有的物理特性。