半参数广义线性模型最大似然估计的弱相合性

赵 瑛

（辽宁开放大学，辽宁沈阳 110034）

0 引言

半参数广义线性模型是由Green和Yandell[1]等一些作者提出来的，相比于通常的广义线性模型，其处理问题更灵活。半参数广义线性模型既含有参数的线性形式，又含有变量的非参数形式。在半参数广义线性模型（SGLMS）中，响应变量 Y∈R，协变量 （X，Z）∈［c，d］p×1×［0，1］，满足给定（X，Z） 时条件期望：

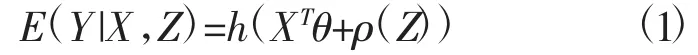
其中，θ∈Θ，ρ∈Ψ。Θ⊂RP是一个非空开集，Ψ是从［0，1］到R的光滑函数的集合，而h是一个从R到R的光滑函数。给定（X，Z）时，Y的条件密度设为指数族形式：

式中，Γ和Φ是R的非空子集，b（φ）是R上的实函数，协变量（X，Z）的联合分布函数G（x，z）未知。

假设（θ，ρ） 是未知参数，在估计未知参数θ的同时，也需要估计半参数ρ，基于未知参数θ的性质，利用 ξ=（X，Z，Y） 的独立同分布的样本ξj=（Xj，Zj，Yj），j=1，2，…，n，得到半参数的最大似然估计量，并且在一定条件下证明其一致弱相合性。

1 最大似然估计

在SGLMS模型中，Y的数学期望μ（φ） 通过 h 与半参数 XTθ+ρ（Z）相联系，即

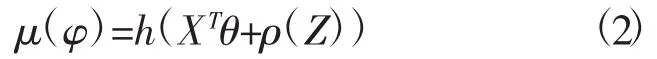
为了表达μ（φ）结构，假设均值μ的逆变换存在，φ=a（XTθ+ρ（Z）），其中 a=μ-1·h。又设 M为R的一个子集，使得对所有的（X，Z）∈［c，d］p×1×［0，1］，θ∈Θ，ρ∈Ψ，有 XTθ+ρ（Z）∈M，则a∶M⊂R→R，而且Φ=a（M）。

假设Φ是自然参数空间的非空凸子集，而自然参数空间是具有有限范数 exp（b（φ））=∫exp（φTy）dλ1（y）的所有φ构成[2]。因此在Φ内，Y的所有阶矩都存在，而且b（φ）的所有阶导数也存在，且

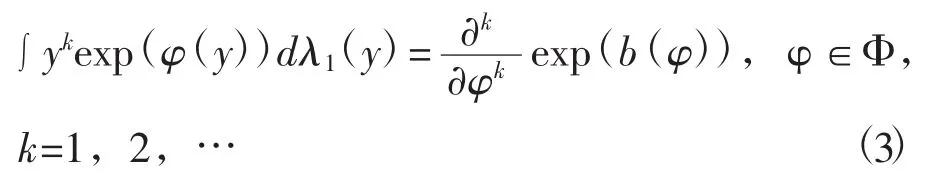
为了讨论Y的各阶矩，需对X、Z的矩进行限制（当X，Z为非随机变量时，下面的假定当然成立）。

假定对 k=1，2，…，p+1 和任意 θ，ρ（Z），

用条件期望重新表达（3），则有

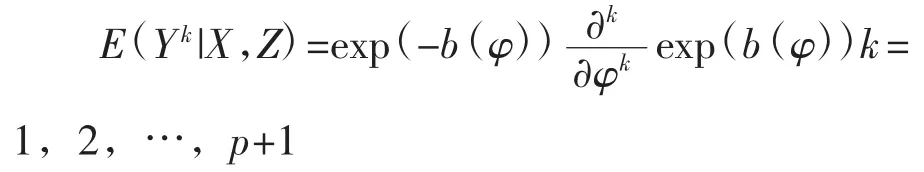
特别对k=1，得

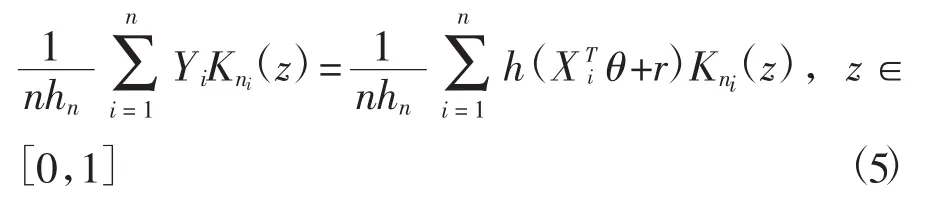
其中Kni（·）=K（（Zi-·）/hn）是带宽hn＞0的通常概率核。

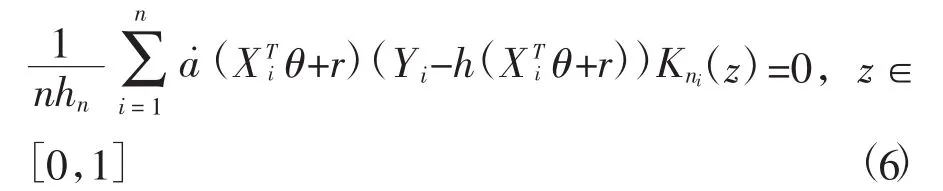
利用普通核估计代替条件期望，得半参数部分 ρ（z）的矩形核估计量为ρM（z）=ρM（z，θ） 方程关于r的解。

2 定理的证明

Severini和Wong[3]提出的最大似然方法，可以构造半参数部分的估计量，并得到了一致收敛的速度，同时证明了

对任意γ＞0成立。其中，q＞2是一个正整数，使得统计量ρθ，ML的q阶矩存在。同时也证明了估计量的导数具有相同的收敛速度。

基于半参数部分的一致弱相合估计的存在性，并将Forrester等人[4]的结果一般化，研究估计量的收敛速度。

为方便起见，引入如下符号：

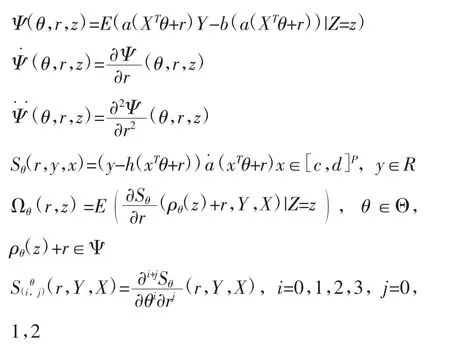
3 结论

这里把Severini和Wong定理中比较苛刻的条件换成了平凡的Lipschitz条件，而且我们得到的结果与Severini和Wong给出的结果比较[5-6]，更具有可操作性，并且则进结论（15），即一步讨论了ρ的导数的最大似然估计的一致弱相合性。