基于改进A*算法和动态窗口法的机器人路径规划*

郭园园,袁 杰,赵克刚

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

1 引言

移动机器人的路径规划主要是搜索出一条无碰撞并且最优的路径[1]。最为常见的路径规划研究主要是基于移动机器人的静态工作环境，常见算法有群智能算法中的遗传算法[2]、粒子群算法[3]、蚁群算法[4]和灰狼算法[5]等，以及经典算法中的人工势场法[6]、RRT(Rapidly exploring Random Tree)算法[7]、A*算法[8]和Dijkstra算法[9]等。然而，机器人工作的地图环境并不是固定不变的，既有可以事先感知到的静态障碍物，也有无法预知的临时障碍物和移动障碍物。移动机器人根据自身安装的传感器检测到一定距离内出现的动态障碍物时，如果继续依照先前在静态环境下规划出的路径移动势必会发生碰撞，导致移动机器人无法完成从起始点至终止点的路径规划。因此，当临时或移动障碍物出现时，为了使机器人能够继续完成路径规划，对于移动机器人进行动态路径规划研究十分有必要。

国内外有众多研究人员对机器人的动态路径规划研究做出了贡献。文献[10]提出了一种基于改进A*算法与动态窗口法的混合算法，有效地克服了传统路径转折角多的缺点，但没有考虑对临时障碍物的处理。文献[11]将入侵杂草算法融合到人工势场算法中，在全局内能够指示性地产生子目标点，引导移动机器人摆脱局部最优，但当目标点附近存在障碍物时，规划路径可能过长甚至规划失败。文献[12]提出了一种改进的RRT算法，通过分支修剪、重新连接和重新生成过程来维护所有节点的有效性，但由于缺少全局最优路径的指引导致遍历空间过大和搜索时间过长。文献[13]将深度强化学习应用于未知环境的动态路径规划，设计了奖惩功能和训练方法，可以对移动障碍物实现避障，但局部规划时获取的不是最短路径，使整体效率下降。

本文针对路径规划领域存在的上述问题，提出了一种改进的A*算法与动态窗口法相结合的混合算法。首先，采用改进的A*算法在静态环境中预先规划出一条全局最优路径，以降低转弯代价和减少遍历节点数;然后,根据规划出的全局最优路径信息和环境中出现的移动障碍物和临时障碍物信息，利用改进的动态窗口法完成局部路径规划，以实现规划的实时性。

2 A*算法

2.1 环境模型的建立

为了解决在复杂环境下的路径规划问题，本文采用栅格法对机器人的工作环境进行建模。其中，已知的固定不变的静态障碍物用黑色栅格表示；机器人可以任意行走的栅格用白色栅格表示。栅格环境模型如图1所示。

Figure 1 Model of raster environment 图1 栅格环境模型

2.2 传统A*算法

A*算法的规划原理主要是：首先，以栅格环境中的起始位置为开始端，搜索起始位置附近8个方向的子栅格位置，每次从这些子栅格位置中选择一个函数评价值最小的子栅格作为下一个搜索的开始端，选中的子栅格被称为当前节点；然后，再次搜索与当前开始端相邻近的子栅格，并从中选取函数评价值最小的子栅格作为新的当前节点，直到当前节点就是终止位置所在的栅格。A*算法的评价函数记作f(n)，如式(1)所示：

f(n)=g(n)+h(n)

(1)

其中,n为当前节点，g(n)为起始点到当前点的代价函数,h(n)为当前点到终止点的启发函数。

3 改进A*算法

传统A*算法规划出的路径有与障碍物棱角存在交点、路径转折点多和路径不平滑等问题，对此本文提出了针对以上问题的改进策略。

3.1 障碍规避策略

传统A*算法在选择当前节点的下一节点时，会首先要求下一节点为非障碍节点，然后在非障碍节点集合中选择评价函数值最小的节点作为当前节点的下一节点。这种选择策略的弊端在于把下一个障碍节点两侧的节点当作可选节点处理了，导致规划出的路径(如图2a中的路径L2)与障碍物(如图2a中的B1和B2)的棱角存在交点甚至会在2个障碍物(如图2a中的B1和B3)的对接棱角之间规划路径(如图2a中的路径L1)，这样降低了移动机器人行走的安全性。

Figure 2 Obstacle avoidance strategy图2 障碍规避策略

针对上述问题，本文提出了障碍规避策略，其原理如图2b所示。中心栅格为当前栅格，将周围的8个节点分为2类：障碍节点影响集合(图2b中和当前栅格挨着的4个障碍栅格所在节点)和障碍节点不影响集合(图2b中的4个拐角处栅格所在节点)。在前者集合中，每个栅格元素两侧的栅格节点可能造成路径与障碍栅格存在交点，将其作为当前栅格的障碍子栅格处理；在后者集合中，每个栅格元素斜对角处的栅格节点对规划的路径不会产生影响，不做处理。采用上述障碍规避策略后，在图2a中规划出的安全路径如路径L3所示。

以上过程可以用式(2)描述说明：

(2)

其中,L-pipi+1表示向量pipi+1的大小，即点pi到pi+1的路径长度；‖pipi+1‖1是向量pipi+1的L1范数；‖pipi+1‖2是向量pipi+1的L2范数；P是本节所定义的障碍节点影响集合；Q是本节所定义的障碍节点不影响集合。

为了验证障碍规避策略的有效性，本文在20×20的栅格地图中与传统A*算法进行了仿真对比实验，规划结果如图3所示，性能对比如表1所示。

Figure 3 Path before and after obstacle 图3 障碍规避前后的路径

表1 障碍规避前后性能对比

从图3可以看出，采用障碍规避策略的A*算法规划出的路径离障碍物有足够的距离，机器人移动起来更加安全。从表1可以看出，采用了障碍规避策略后，总遍历节点数减少了31%，运行时间缩短了15%，考虑安全距离后路径长度增加8%，但从路径的安全性上考虑，改进效果明显。

3.2 递归二分法优化策略

从图3中规划出的路径可以看出，路径经过多次转折，导致路径不是最短的且平滑度较差，本文对A*算法规划出的路径采用递归二分法优化策略删除冗余节点，减少转折度数和路径长度。具体原理如下所示：

(1)判断2点之间的连线有无障碍物。如图4a所示，判断A点和E点之间是否存在障碍物，已知A、E2点的信息，可以确定A点和E点的中点C的信息，以此中点分别向两边递归查找，分别得到AC线段的中点B和CE线段的中点D,判断B点和D点所在的栅格的代价值(障碍栅格代价值为1，自由栅格代价值为0)，通过计算可以得出，这2点的代价值均为1，表明A点和E点的连线上存在障碍物。

(2)剔除直线冗余点。如图4b所示，去除实线的冗余节点，首先将A点作为初始判断节点，从第3个节点C点开始判断，看到A点和C点之间的连线不存在障碍物，说明第2个节点B点是冗余节点，将其剔除，C点成为新一轮的第2个节点；对新一轮的第3个节点D点进行判断，发现在A点与D点中间并不存在障碍，说明新一轮的第2个节点C点为冗余节点，将其去除，则D点成为下一轮的第2个节点；以此类推，直到F点成为第2个节点，这时G点和A点的连线之间存在障碍物，将F点作为转折点保存下来，G点是目标点，循环到此结束，最终判断出来的路线节点为：A、F和G。

以上过程可以用式(3)和式(4)描述说明：

(3)

(4)

其中,L={Li|i=1,2,…,N},表示未采用优化策略之前路径点的集合,N表示路径上的节点数；Lr为单元栅格的代价值，障碍栅格代价值为1，自由栅格代价值为0；{xLi+j|j=1,2,…,xLi+2-xLi-1}为路径点Li和Li+2之间的单位距离的点的集合；O为障碍栅格的集合；F为自由栅格的集合；LU{Li+1}为集合{Li+1}相对于集合L的补集;l表示采用优化策略之后路径点的集合。

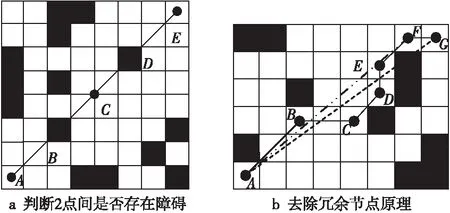
Figure 4 Optimization strategy of recursive dichotomy图4 递归二分法优化策略

为了验证递归二分法优化策略在去除冗余节点方面的有效性，本文在20×20的栅格地图中与只采用了障碍规避策略的A*算法进行了仿真对比，规划结果如图5所示，性能对比如表2所示。

从图5可以看出，采用递归二分法优化策略的A*算法规划出的路径长度和转折次数明显减少。

Figure 5 Path before and after removing redundant points图5 去除冗余节点前后路径

表2 去除冗余节点前后性能对比

从表2可以看出，去除冗余节点后，总转折次数减少46%，路径长度缩短6%，总转折角度减小57%，改进效果明显。

3.3 动态内切圆平滑策略

在静态障碍环境下，路径的安全性和平滑性是移动机器人路径规划需要考虑的重要指标。由于将路径的折线型优化成弧线型更有利于机器人的移动，本文提出动态内切圆平滑策略，将折线角优化成弧线角。

基于动态内切圆平滑策略规划出的某条路径如图6所示，经过节点A(xA，yA)、B(xB，yB)、C(xC，yC)和D(xD，yD)，路径的起始位置为A，终止位置为D。具体实现步骤如下所示：

步骤1计算路段AB和路段BC的长度，再选取较短路段AB的首端点A为第一次切点，过点A的垂线与∠B的平分线交于点c1(xc1，yc1)，即过A的内切圆的圆心。

过点A和点B的一般式直线方程如式(5)所示：

Figure 6 Smoothing strategy of dynamic inscribed circle图6 动态内切圆平滑策略

(yB-yA)x+(xA-xB)y+C1=0

(5)

直线Ac1和AB垂直，其一般式直线方程如式(6)所示：

(xA-xB)x+(yA-yB)y+C2=0

(6)

过点B和点C的一般式直线方程如式(7)所示：

(yC-yB)x+(xB-xC)y+C3=0

(7)

由点n1在直线BC上，可得式(8)：

(yC-yB)xn1+(xB-xC)yn1+C3=0

(8)

式(5)～式(7)中的C1、C2和C3是常数，分别为(yAxB-yBxA)，(xB-xA)xA+(yB-yA)yA和(yBxC-yCxB)。

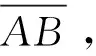
(9)

(10)

(11)

由式(9)～式(11)联立可求得点n1的坐标，进而得直线n1c1的一般式方程,如式(12)所示：

(xn1-xB)x+(yn1-yB)y+C4=0

(12)

其中，C4是常数，其值为(xB-xn1)xn1+(yB-yn1)yn1，联立式(6)和式(12)可求得交点c1的坐标。

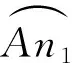
圆心c2到直线AB的距离如式(13)所示：

(13)

由余弦定理可求得∠B的角度：

(14)

根据三角形Bc2m2的边角关系可得式(15)：

(15)

圆c2的方程设为式(16)的形式：

(16)

从选取的内切圆c2应满足的第2个条件可知，内切圆上的顶点坐标为(xo1，yo1)，满足如式(17)的关系式：

(17)

(18)

当式(18)取等号时，内切圆c2恰好与障碍物的顶点相交；当式(18)取大于号时，障碍物的顶点在内切圆的内部。

步骤4判断用劣弧代替的折线的转折点是否是规划路径的最后一个转折点，如果不是，返回步骤1，继续执行后续路段的平滑处理；如果是，结束执行。

4 改进动态窗口法

在动态环境下进行路径规划时，需要考虑突然加入的临时障碍物和活动的移动障碍物产生的影响，这就要求机器人能够局部实时避障，对此本文引入了动态窗口法来解决这个问题。

4.1 运动学模型

动态窗口法的思路是在由线速度和角速度组成的集合{(ν，ω)}中采样多组速度，并分别模拟这些速度在下一个周期内的轨迹，然后通过评价函数对各组轨迹进行评估选取最优轨迹。因此，可得如式(19)～式(21)所示的运动学模型：

xt+1=xt+ν·Δt·cos(θ(t))

(19)

yt+1=yt+ν·Δt·sin(θ(t))

(20)

θ(t+1)=θ(t)+ω·Δt

(21)

其中,xt+1是t+1时刻的运动坐标，ν是时间间隔Δt内的线速度，ω是时间间隔Δt内的角速度，θ(t)表示机器人的运动方向与水平方向的夹角。

4.2 速度采样空间

在移动机器人的速度空间中，存在多个速度组(ν，ω)。但是，因为机器人受到自身硬件和外在环境约束其速度被限制在一定范围内，约束条件如下所示：

(1)移动机器人的速度约束如式(22)所示：

Vm={(ν,ω)|ν∈[νmin,νmax],

ω∈[ωmin,ωmax]}

(22)

(2)在预测时间间隔内受电机加减速性能约束,如式(23)所示：

(23)

(3)为保证机器人实现安全动态避障，需要与障碍物发生碰撞前以最大减速度，将速度降至0，其刹车速度约束如式(24)所示：

(24)

其中，dist(ν，ω)表示机器人在速度(ν，ω)下与障碍物的最近距离。

4.3 改进评价函数

满足约束条件的速度采样空间内，仍有一些对应的预测轨迹是可行的，本文通过评价函数对这些预测轨迹进行评估。对于传统的评价函数，存在以下问题：目标点附近存在障碍物导致路径变长甚至规划失败；遇到凹型槽类障碍物易陷入局部最优；与A*算法相结合导致局部路径与全局最优路径距离较远。针对上述问题，本文在评价函数中加入了轨迹末端到目标点的距离和轨迹末端到全局最优路径的距离，改进后的评价函数如式(25)所示：

G(ν,ω)=σ(α·DP(ν,ω)+β·DT(ν,ω)+

δ·DO(ν,ω)+γ·V(ν,ω))

(25)

其中,DP(ν，ω)为结合全局最优路径的方位角评价函数，表示预测轨迹末端到全局最优规划路径的最短距离；DT(ν，ω)表示预测轨迹末端到目标点的欧几里得距离；DO(ν，ω)表示预测轨迹末端到障碍物的距离；V(ν，ω)为预测速度大小的评价函数。加权系数包括α,β,δ,γ,σ∈(0,1)，且β+δ=1。

为了验证动态窗口法中加入轨迹末端到目标点距离的有效性，在20×20的栅格地图中进行了仿真实验，规划结果如图7所示。

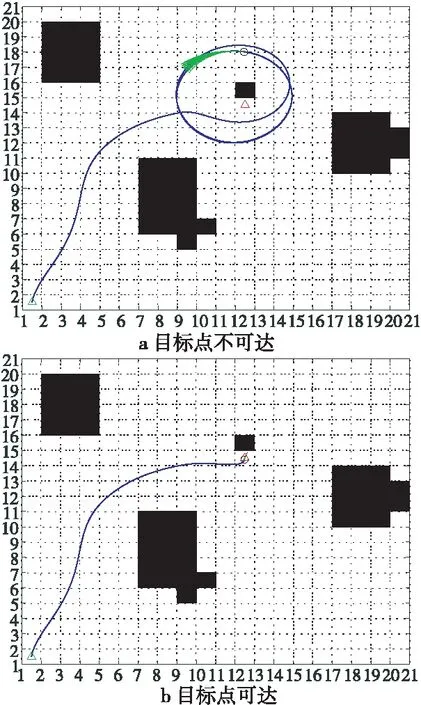
Figure 7 Obstacles near the target point图7 目标点附近存在障碍物

从图7可以看出，当目标点附近存在障碍物时，传统的动态规划算法检测到当前点与障碍物的距离过近，DO(ν，ω)所占的比重变大，轨迹末端远离障碍物，导致在目标点附近循环转圈致使路径规划失败；改进的动态窗口法规划的轨迹快到达目标点时，DT(ν，ω)所占的比重变大，使障碍物对轨迹末端的影响变小，可以直接到达目标点。

5 仿真与分析

为了分析评价本文的改进A*算法和混合算法在复杂环境下路径规划的质量，在Matlab2018a环境下对本文提出的算法进行仿真验证。

5.1 静态环境下改进A*算法的仿真对比

为检验所提改进A*算法在地图环境中进行路径规划的有效性，将动态内切圆平滑策略分别应用到文献[14]的蚁群算法、Dijkstra算法和传统的A*算法中并进行仿真，得到的结果如图8所示，改进A*算法与其他算法的性能对比如表3所示。

Figure 8 Simulation comparison of four algorithms in static environment图8 静环境下4种算法仿真对比

从图8中可以看出，改进A*算法规划出的路径更加平滑和安全，结合表3的数据，与传统A*算法相比，在转折角度和遍历节点数方面分别减少了27.5 %和28.2%；对节点的特殊处理使路径长度仅减少了4.4%；与其他算法相比本文改进A*算法效果提高明显。综合来看，对A*算法的改进增加了路径的平滑性，缩小了搜索空间，缩短了运行时间，增加了安全性。

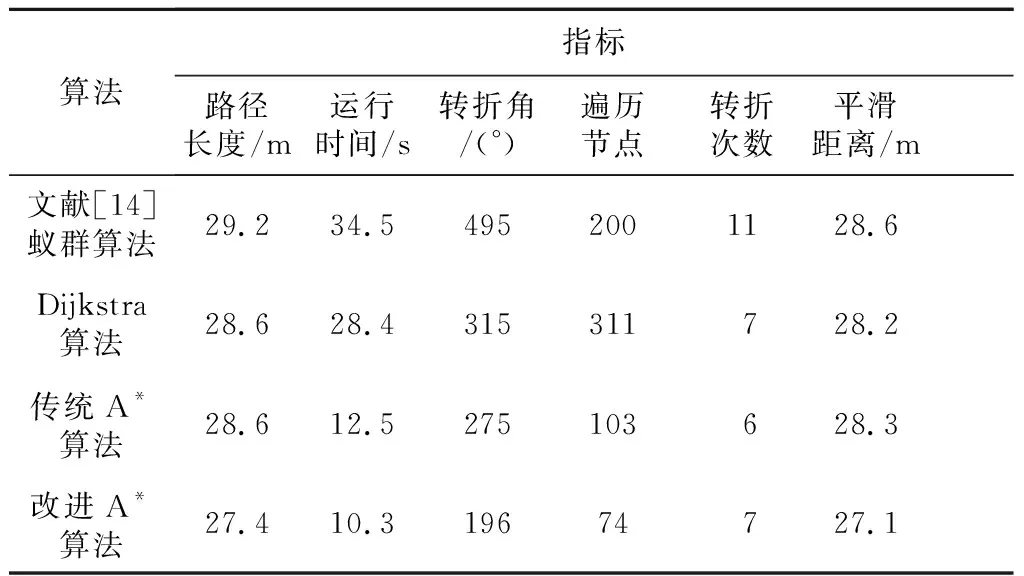
Table 3 Comparison of performance of four algorithms in static environment表3 静态环境下4种算法性能对比

5.2 动态环境下混合算法的仿真对比

将改进A*算法与动态窗口法相结合，先用改进A*算法规划出一条全局最优路径，再使用动态窗口法进行局部避障，以解决动态环境下的路径规划问题。

5.2.1 凹型槽问题的仿真

动态窗口法在面对凹型槽类障碍物时，容易陷入局部最优，在凹型槽内180°翻转循环会导致路径规划失败。将动态窗口法与A*算法相结合后，借助于A*算法的全局最优路径(虚线)指引，动态窗口法在局部规划时能够跳出局部最优到达目标点，仿真对比结果如图9所示。

Figure 9 Simulation result of concave groove problem图9 凹型槽问题仿真结果

5.2.2 临时障碍物环境下的仿真

为了检验混合算法在动态环境下的规划能力，在规划好的全局最优路径上加入临时障碍物，并与传统的混合算法、文献[15]中的混合算法进行仿真对比，结果如图10所示，性能指标对比如表4所示。

Figure 10 Comparison of path planning results of hybrid algorithms in temporary obstacle environment图10 临时障碍物环境下混合算法路径规划结果对比

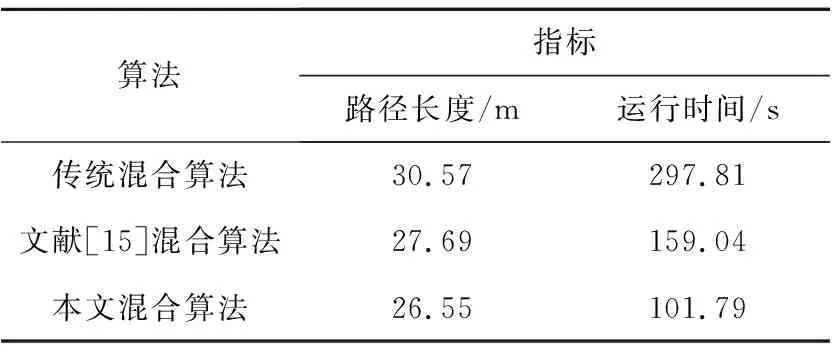
表4 临时障碍物环境下3种算法性能对比

从图10中的规划结果来看，传统混合算法偏离全局最优路径(虚线)较远，在保障移动安全的情况下，本文混合算法比文献[15]的混合算法更加贴合全局最优路径。从表4中得出，与传统混合算法和文献[15]混合算法相比，本文混合算法路径长度分别缩短了13.2%和4.1%，运行时间分别缩短了65.8%和36.0%，说明本文所提算法在路径长度和运行时间上均优于其他2种算法。

5.2.3 移动和临时障碍物环境下的仿真

为了进一步检验混合算法的有效性，在规划好的全局最优路径上加入临时障碍物的同时，在栅格地图中再加入移动障碍物，并增加地图环境的复杂度。与传统的混合算法、文献[15]中的混合算法进行仿真对比，结果如图11所示，性能对比如表5所示。

Figure 11 Comparison of path planning results of hybrid algorithms in moving and temporary obstacles environment图11 移动和临时障碍物环境下混合算法路径规划结果对比

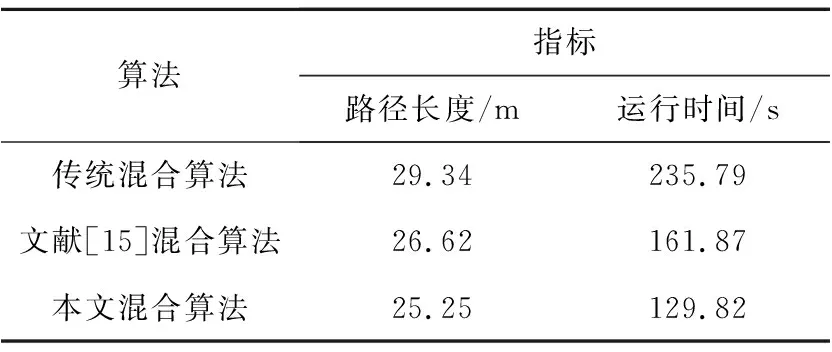
表5 移动和临时障碍物环境下3种算法性能对比

从图11中的规划结果来看，3种混合算法均能躲避移动障碍物，本文混合算法比其他2种混合算法更加贴合全局最优路径(虚线)。从表5中可知，与传统混合算法和文献[15]中混合算法相比，本文混合算法的路径长度分别缩短了13.9%和5.1%，运行时间分别缩短了44.9%和19.8%，说明本文所提算法在路径长度和运行时间上均优于其他2种算法。

6 结束语

为了提升移动机器人在复杂环境下路径规划的效率，本文提出了一种改进A*算法和动态窗口法相混合的算法。在静态环境下，在改进A*算法的基础上结合障碍规避策略提升路径安全性，结合去除冗余节点策略减小转折角度，再结合动态内切圆平滑策略增加路径平滑度；在动态环境下，改进动态窗口法实时规划路径，弥补了A*算法在实时规划方面的不足，在躲避临时和移动障碍物时能规划出一条最优路径。通过实验与其他算法进行性能对比，验证了本文所提算法的有效性。下一步计划在特定的场合下进一步采用定量的理论分析来说明路径规划的收敛情况，或把该算法运用在多机器人的协同作业或物流机器人的配送上以进一步验证该算法在现实环境中规划的路径质量。