渐近圆锥天线等效电路模型分析

郭景海，马 良，程引会，吴 伟，王旭桐，刘逸飞，李进玺，王文兵

(强脉冲辐射环境模拟与效应国家重点实验室； 西北核技术研究所： 西安 710024)

高空核爆炸及雷电等过程会产生一种电场强度高、前沿快、频带宽及作用范围大的电磁脉冲，对作用范围内的电力系统及电子设备等造成干扰或破坏。为进行电磁脉冲防护，需了解其信号特征，电磁脉冲电场测量是其中一项重要的基础工作。

渐近圆锥天线是一种常见的D-dot型脉冲电场测量探测器，具有频带宽及环境稳定性好的特点，且天线的等效面积和等效电容具有解析解[1-4]，被广泛应用于电磁脉冲电场测量工作[5-9]。当被测电场频率较低时，渐近圆锥天线的寄生电感可忽略，探测器可近似地等效为一阶RC电路模型，天线负载上为被测电场的微分信号[10-15]。当被测电场信号上升沿很快时，电场信号包含较多的高频分量，采用一阶RC模型所得电场信号会出现不同程度的振铃，使测量结果产生较大偏差。振铃现象只有二阶及以上电路模型才可能出现，说明测量快信号时，天线的寄生电感不可忽略，需使用二阶RLC等效电路模型。但渐近圆锥天线的寄生电感很难用解析或数值方法得到，文献[2]给出了渐近圆锥天线寄生电感参数的值，但并没有给出获取方法；文献[16]指出渐近圆锥天线可等效为二阶RLC电路模型，但并没有给出寄生电感参数及获取方法，而是采用全波电磁仿真的方法计算了天线的频率响应。针对该问题，本文提出了一种渐近圆锥天线寄生电感的获取方法，建立了实用的等效电路模型，利用该模型可准确方便地重建被测电场波形。

1 基本原理

1.1 渐近圆锥天线解析模型

渐近圆锥天线的等效面积Ae、等效高度he及等效电容Ce等电参数具有严格的解析解，可用等效电荷法推导出渐近圆锥天线电参数的解析公式[1-3]。在柱坐标下，假设线电荷分布于±z轴，±z轴上线电荷密度相同，极性相反，长度均为z0，则线电荷密度σ(z)可表示为

(1)

其中，σ0为常数。这两段线电荷在空间产生的电势φ为

(2)

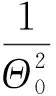
(3)

其中，ρ为柱坐标系半径方向的长度。

图1为渐近圆锥天线轮廓线示意图。

一个该等位线形状的良导体必然是一个电势为φ的等势体，0电势面为xy平面。良导体等位面上的电荷量Q=σ0z0，则上下镜像2个等位面之间的电容Ce为

(4)

上述物理模型可看作一个具有线电荷密度的偶极子，偶极矩可表示为

(5)

该偶极子天线的等效高度he为

(6)

天线等效高度he与等效面积Ae之间的关系可表示为[15-16]

(7)

由式(4)、式(6)和式(7)可得渐近圆锥天线的等效面积Ae，可表示为

(8)

当z→0时，ρ/z=tanθ0，θ0为渐近圆锥天线顶点处的半锥角，φ可表示为

(9)

结合式(2)，可得

(10)

由式(10)可知，Θ0是与渐近圆锥天线顶点处锥角θ0有关的参数。

上述推导过程可得偶极渐近圆锥天线的电参数和几何参数。单极渐近圆锥天线的等效高度hm、输入电容Cm及等效面积Am与偶极渐近圆锥天线电参数的关系可表示为

hm=he/2；Cm=2Ce；Am=Ae

(11)

因此，单极渐近圆锥天线的电参数为

(12)

1.2 单极渐近圆锥天线等效电路模型

单极渐近圆锥天线属于D-dot传感器，输出量为电位移矢量D的微分，而自由空间中电位移矢量D与电场强度E满足D=ε0E。图2为单极渐近圆锥天线的二阶RLC诺顿等效电路。

其中：i(t)为等效电流源；L为单极渐近圆锥天线寄生电感；R为天线负载；Vo为负载上的输出电压。

分析等效电路可得到[17-19]

(13)

其中，Ez为z方向电场强度。方程两边同时对时间积分，可得到单极渐近圆锥天线基于二阶等效电路模型的电场强度重建公式

(14)

令L=0，则回归到单极渐近圆锥天线基于一阶等效电路模型的电场重建公式

(15)

根据前述理论分析，单极渐近圆锥天线的等效面积Am和等效电容Cm均可解析计算，因此只要求得单极渐近圆锥天线的寄生电感L，就可利用式(14)重建被测电场波形。

在频域内，对图2所示等效电路进行分析，可得Vo为

(16)

其中，ω为角频率。假设被测电场波形为E0sin(ωt)，E0为电场幅度。则Vo幅度可表示为

(17)

结合式(17),可得基于二阶等效电路模型的单极渐近圆锥天线的幅频特性G2(ω)，可表示为

(18)

令L=0，则回归到基于一阶等效电路模型的单极渐近圆锥天线的幅频特性G1(ω)，可表示为

(19)

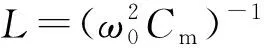
完整的幅频特性曲线可用实验方法得到，但需大功率及高带宽的功放，实现的困难较大。本文将采用全波电磁仿真方法获得单极渐近圆锥天线的幅频特性曲线。

2 仿真分析

取单极渐近圆锥天线参数Θ0=0.3,z0=10.0 mm，由式(12)计算得到Am=2.61×10-4m2，Cm=4.61×10-13F，hm=5.0 mm。利用微波工作室CST瞬态求解器进行全波电磁仿真，建立了单极渐近圆锥天线仿真模型，如图3所示。天线尖端连接同轴传输结构的内导体，传输线内外导体间连接50 Ω集中负载。在该模型中，接地平面采用金属屏蔽腔体代替，腔体上表面视为单极渐近圆锥天线的接地平面，同时，腔体也为天线负载响应Vo的监测提供电磁屏蔽。模拟过程中，采用平面波作为激励源，平面波电场极化方向为y方向，垂直于接地平面；在±x，±z和-y方向采用open类型吸收边界，用于模拟无限大接地平面[20-21]，在+y方向采用open(add space)类型边界用于截断无限大空间；模拟频率设置为0～10 GHz。

图4为全波电磁仿真单极渐近圆锥天线幅频特性曲线。由图4可见，当ω0=2πf0=32.42 GHz时，寄生电感L=2.06 nH。至此，单极渐近圆锥天线二阶RLC等效电路模型的所有参数都已确定，利用式(14)由负载响应Vo便可重建被测电场。

为验证等效电路模型参数的准确性，分别计算了一阶RC等效电路模型与二阶RLC等效电路模型的幅频特性G1(f)和G2(f)，并与全波电磁仿真结果进行了比对。3种方法得到的幅频特性曲线，如图5所示。

由图5可见：二阶等效电路模型与全波电磁仿真结果吻合较好；在10 GHz以内，渐近圆锥天线可较好地等效为图2中的二阶电路模型；而一阶等效电路模型在低频时与仿真结果吻合较好，但高频时的差异较大。用G2(f)-G1(f)表示一阶与二阶等效电路模型幅频曲线的偏差，G2(f)-G1(f)随频率的变化关系如图6所示。由图6可见：当频率低于3.12 GHz时，2种等效电路模型的幅频特性偏差小于3 dB；当频率小于1.71 GHz时，二者的偏差小于1 dB。

为直观展示2种等效电路模型对被测电场时域波形重建的影响，利用图3所示模型对不同入射电场激励时，单极渐近圆锥天线的响应进行了全波电磁仿真模拟。CST模拟过程中，入射电场信号选用幅度为1 V·m-1的方波，入射电场波形的上升时间tr分别取0.2，0.6，1.0，2.0 ns，方波平顶持续时间为5 ns，仿真得到的渐近圆锥天线负载输出电压Vo与入射电场上升沿的关系，如图7所示。

将仿真得到的Vo分别代入式(15)和式(14)对应的一阶和二阶等效电路模型的电场强度重建公式，对被测电场波形进行重建。图8为2种等效电路模型重建的被测电场波形。由图8可见，二阶等效电路模型较为准确地还原出了入射电场的幅值和波形特征。一阶等效电路模型还原的入射电场波形出现了过冲现象，tr越短过冲越大。当tr为0.6 ns时，过冲为5%，而当tr为0.2 ns时，过冲达到了11%。因此，当电场测量精度要求较高时，采用二阶等效电路模型重建被测电场更合理。

3 结论

本文分析了渐近圆锥天线的等效电路模型，提出了利用电路谐振频率结合全波电磁仿真方法获得渐近圆锥天线寄生电感的方法，从而得到了二阶RLC等效电路模型的全部参数。对比渐近圆锥天线一阶和二阶等效电路模型对被测电场的重建效果，表明，在被测电场前沿上升时间较短时，一阶等效电路模型重建的被测电场的结果存在较大偏差，而二阶等效电路模型对被测电场的重建结果更准确。