考虑时间窗约束的多无人机任务分配
2022-08-11魏兆恬赵晓林李俊涛纪良杰
魏兆恬, 赵晓林, 李俊涛, 纪良杰
(空军工程大学,a.研究生院; b.装备管理与无人机工程学院,西安 710000)
0 引言
随着人工智能技术快速发展,无人机(UAV)相关技术也在朝着智能化的方向发展。在现代战场侦察、攻击等任务中,无人机因其灵活、隐蔽等特点而被广泛使用。单架无人机可以独立地完成侦察、攻击等一系列作战任务。但由于其任务执行能力差、效率低,在面对更为复杂的作战任务时往往需要多架无人机协同的方式进行[1]。多无人机系统是由多架同构或异构无人机组成,相比于单架无人机具有明显的优势,可以有效地提高任务的可靠性。多无人机的任务规划问题是其进行高效协同作战的关键。如何对任务区进行合理的最优化分配仍是当前研究的重点。
多无人机任务分配问题的建模方法,可归纳为旅行商问题(Travelling Salesman Problem,TSP)模型[2]、定向问题(Orientation Problem,OP)模型[3]、其他模型以及随之衍生出的拓展模型[4]。TSP模型假设无人机会对所有目标访问一遍,并最终回到出发点。将多无人机拓展到TSP模型中可得到MTSP模型,该模型可用于对多无人机协同任务分配问题的研究。车辆路径问题(Vehicle Routing Problem,VPR)模型是TSP模型的另一种拓展模型。在该模型中,无人机的燃料、载弹能力、侦察载荷等约束条件被视为车辆的运载能力,侦察、攻击任务被视为“客户”。VPR模型能够在车辆运载能力的范围内尽量满足客户的需求。OP模型中,无人机可以对执行的目标进行选择,使各无人机在自身的能力范围内找到最优的任务分配方案。因此,OP模型更能满足实际战场环境的需要,得到了广泛的应用。
任务分配问题的求解方法可分为集中式、分布式、混合式等。应用较多的群智能算法就是集中式求法中的启发式算法。文献[5]针对多无人机动态侦察资源分配问题提出了一种改进的人工蜂群(Artificial Bee Colony,ABC)算法。基于合同网的拍卖算法[6]是应用广泛的一种多无人机的任务分配算法,该方法是一种分布式智能优化算法,它通过防止冲突,对每个任务进行通信协商来解决问题。整个过程可分为“招标-投标-中标-确认”4个阶段。拍卖算法的演化算法被广泛地提出,如基于共识的捆绑算法(Consensus-Based Bundle Algorithm,CBBA)[7],使用这种算法可以获得无冲突的最优解。CBBA算法被提出后,国内外学者就算法的改进做了诸多研究。针对异构多无人机协同侦察任务决策问题,文献[8]提出了一种分布式的扩展CBBA算法;文献[9]通过更改本地拍卖信息的存储方式,提出新的冲突分配解决办法,从而解决在轨装配航天器的任务分配问题;文献[10]提出了异步CBBA(ACBBA),它通过一组新的本地消除冲突规则,不需要访问全局信息状态,在保持收敛特性的同时最小化通信负载和时间延迟,并且它使用相对较小的带宽并且不需要人为的时间延迟来产生一致的任务分配。
本文在现有研究的基础上,以异构多无人机执行带有时间窗约束的侦察、攻击任务为场景,以任务执行收益为目标,在无人机的任务执行能力、载弹能力以及任务执行时间的约束下,通过引入时间窗约束的CBBA算法消除了任务冲突,实现了合理分配。
1 问题描述和数学模型
1.1 问题描述
在现代化的战场环境中,多无人机在参与战争时,需要先对目标区域进行侦察,侦察完毕后再对其进行打击,这种作战模式带来的一个关键问题就是异构多无人机多任务分配问题。针对上述问题,本文的描述如下:多无人机飞往任务区执行侦察、攻击任务。首先考虑无人机与目标点的距离、到达目标点的时间等条件的约束。在执行攻击任务时,一些目标需要多枚武器才能够摧毁,且无人机的载弹量有限,只能装载一定数量的武器。


在完成任务之后,无人机将获得收益。问题的关键在于如何在综合各种约束条件的前提下,一方面实现无人机收益的最大化,另一方面实现最短的完成任务时间。为了简化问题,提出如下假设:1)各无人机在执行任务时的速度一致,即不考虑无人机之间的碰撞问题;2)无人机对于每个任务的选择可能性相同;3)不考虑无人机飞行过程中的转弯半径;4)不考虑油耗代价的影响,即每架无人机的油量充足;5)作战任务区域中每个攻击任务的类型相同。
1.2 数学模型
1.2.1 目标函数
对于每个任务设置时间窗Wj=(tj,start,tj,end,tj,last),其中,tj,start为任务开始的时间,tj,end为任务结束的时间,tj,last为任务的持续时间。无人机Ui沿着路径pi执行任务k的收益为
(1)
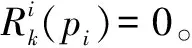
无人机在执行任务时存在任务风险,任务风险程度由无人机自身的任务执行能力和任务威胁程度决定,任务风险表示为
(2)
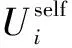
无人机在沿路径pi执行任务k的过程中会产生距离折扣,它与无人机沿路线飞行的距离有关。飞行距离越长,折扣越大。飞行距离和折扣函数可以表示为
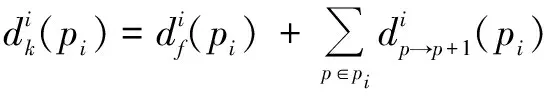
(3)
(4)
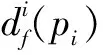
根据式(1)、式(2)、式(4)可得到代表任务效益的函数为
(5)

本文设计的目标是对任务进行分配,使多无人机执行任务的收益最高,飞行距离最短。综上可得目标函数为
(6)
1.2.2 约束条件
每个任务需要多枚武器以确保完全摧毁目标。此外,每架无人机有一定的载弹能力,其所使用的武器总数不超过每架无人机的载弹总数。
1) 对于侦察任务,无人机的任务执行能力约束为
(7)
表示每架侦察无人机Ui所能执行的侦察任务数量不超过其所能执行的最大任务数量。
2) 对于攻击任务,无人机的任务执行能力约束为
(8)

3) 每个任务要求必须在任务时间窗内完成,即
μi(pi)=max(tj,start,tj,arrive)μ(pi) (9) CBBA算法由两个阶段构成,即任务包构建阶段和冲突消解阶段,算法在这两个阶段迭代[11-12]。在任务包构建阶段,每个代理将任务插入到自己的路径中,并进行排序,直到所有任务均被分配完毕或代理的载荷资源被耗尽为止。在冲突消解阶段,消除代理之间的任务冲突,使利益最大化。算法流程如图1所示。 图1 CBBA算法流程图Fig.1 Flow chart of CBBA algorithm 在CBBA算法中,不同无人机的任务分配和通信中介是独立的。每架无人机都有一定的信息,如下所述。 1)Bi为任务包集,包括无人机Ui在任务空间上已知的所有任务。Bi表示无人机Ui通过竞拍获得的依次排列的任务序列,若无人机Ui尚未竞拍到任务,则Bi=∅。 2)pi为路径集,代表无人机Ui分配到的所有任务,按照执行的先后顺序排列。 每架无人机构建一个任务包,根据自己的载弹能力将能使自己的收益达到最大的任务依次加入到任务包中,按照无人机计划完成任务的顺序进行排序。用Bi表示添加到无人机Ui的一组任务,pi表示任务包中任务的分配顺序。当向任务包中插入任务Tj导致得分增加,则可以表示为 (10) (11) (12) (13) (14) pi=pi⊕ni,j*{j*}。 (15) 在任务包构建完成之后,无人机之间需进行通信来交流竞拍得到的任务信息。无人机需要考虑自己对所选任务的出价是否高于最高出价,以及每个任务可以被分配的无人机,这就需要一定的规则来消解冲突。冲突消解的目的就是确保每个任务只能分配给一架无人机。 在CBBA算法中,无人机根据其当前分配的任务集将任务添加到其任务包中。因此,如果一架无人机对某一个任务的出价高于其他无人机,它也应该释放在它之后添加到包中的任务,因为它们可能不再是最佳选择。通过允许无人机出价高于较早选择的任务,该算法能够完成比以前的迭代方法更有价值的任务。但这也导致了算法更加复杂,为了避免多架无人机分配到相同的任务,需要一定的冲突消解规则来解决这一问题。 在冲突消解阶段,每架相邻的无人机之间通过交互通信共享以下3个信息:1) 中标任务集合Yi;2) 中标无人机集合Zi;3) 其他每架无人机最后一次更新消息的时间Si。 在接收到信息之后,无人机Ui会通过比较来确定自己能否中标。如果Ui的出价更高,则它将通过竞争得到任务Tj,那么其他在任务集中含有任务Tj的无人机将会释放任务Tj,路径集中任务Tj之后的所有任务也会随之被删除,在下一次的迭代中进行重新分配。 表1 接收者Ui对于发送者Uk信息所采取的方案 收到信息后,无人机会根据表1中方法验证哪些信息状态是正确的,并采取相应的行动。在表中,Zi有4种不同的考虑情况:1) 认为发送者Uk中标;2) 认为接收者Ui中标;3) 认为其他无人机Um中标,发送者Uk认为Zi是Um时,在接收者中会增加考虑不是Ui,Uk,Um的情况,即Un;4) 不知道谁赢得投标,即∅。 如果出价列表在第2阶段被更改,且更改的任务在其任务包中,则释放此任务以及在它后面添加到任务包中的所有任务。相应的Yi,Zi重置,即:Yi,bin=0,Zi,bin=∅,bin=∅。通过这种方式解决在分配过程中的任务冲突,然后算法会重新返回第1阶段继续添加任务。算法会一直迭代这两个阶段直到相应的Yi,Zi不再发生变化,表明所有的冲突被消解完毕,证明各无人机已完成对各攻击目标的分配方案。 设计采用侦察、攻击无人机分别执行侦察和攻击的任务。侦察任务的时间窗口为5 min,攻击任务的时间窗口为15 min。假设执行攻击任务的无人机和执行侦察任务的无人机的飞行速度相同,并且有充足的油量维持飞行。为了验证算法的可靠性,选取6架侦察无人机,4架攻击无人机,11个侦察任务,9个攻击任务。多无人机的位置坐标及类型如表2所示。在引入时间窗的情况下,仿真结果如图2所示。每架无人机具体执行任务的时间表如图3所示。 表2 无人机属性 图2 带有任务窗的任务分配细节图Fig.2 Task allocation details with task window 图3 每架无人机具体分配时间图Fig.3 Specific time allocation of each UAV 图2显示了X,Y轴随时间的位置变化。从图中可以看出,多无人机已经完成了所有子任务,且每架无人机之间在执行任务时不存在任务冲突。 图3显示了每架无人机的具体任务分配时间表。用矩形的长短表示时间窗的不同。从图3可以看出,由于每架无人机的能力不同,在任务分配中有些无人机可能执行多个任务。此外,在侦察和攻击任务时间窗不同的情况下,该算法可以成功地解决带有复杂时间约束的多任务分配问题。 综合图2、图3可以得出,实验所得到的任务分配结果合理并且达到了预期的效果。在相同的情况下,将引入时间窗的CBBA算法(即本文算法)与未引入时间窗的CBBA算法进行对比,如表3所示。 表3 两种算法任务分配结果对比 通过两种算法的对比可以看出,引入时间窗后的任务收益明显提高,这是由于无人机对目标进行侦察、攻击时,如果停留的时间过长,容易被目标发现并被摧毁,使无人机的任务执行效率降低。引入时间窗之后,多无人机在执行任务过程中被发现的概率会降低,提高了任务的完成效率,能够得到更高的任务收益。图4所示为每个任务下无人机的毁伤概率,从中可以看出,使用引入时间窗的CBBA算法的无人机在执行任务时,毁伤概率大大降低。由此可知,本文算法明显优于未引入时间窗的CBBA算法。 图4 每个任务下无人机的毁伤概率Fig.4 Damage probability of UAV in each task 本文研究了异构多无人机的多任务分配问题。在进行任务分配的过程中考虑了以下限制:无人机的载弹能力、任务的时间窗,引入了基于无人机飞行距离的折扣函数进一步优化任务分配方案,通过对发送者与接收者无人机对于任务竞价分数的各种情况的分析,成功地消除了在任务分配阶段产生的冲突。利用CBBA算法对侦察、攻击两种任务进行分配,并进行了仿真实验与分析。实验证明,算法能够在任务不同时间窗的情况下对任务进行合理的分配,执行任务的收益明显高于未引入时间窗的CBBA算法。综上所述,根据本文提出的异构多无人机多任务分配算法可以得出在任务分配过程中的无冲突的方案,能够保证多任务的成功分配。但在实际的战场环境中,无人机在执行作战任务时可能遇到雷达、障碍物等威胁,可能存在执行任务区的数量发生骤降的情况,无人机本身也会出现突发故障等情况。因此,多任务区任务分配方案的实时性问题将是接下来研究的重点内容。2 CBBA算法设计

2.1 信息结构
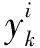


2.2 任务包构建

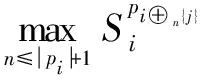
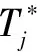

2.3 冲突消解

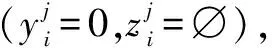

3 仿真验证
3.1 任务场景
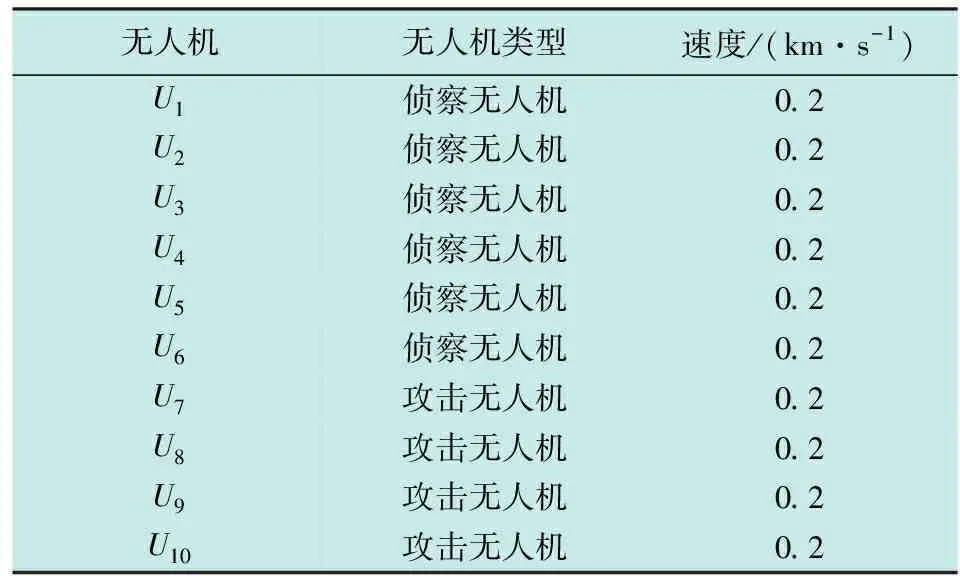
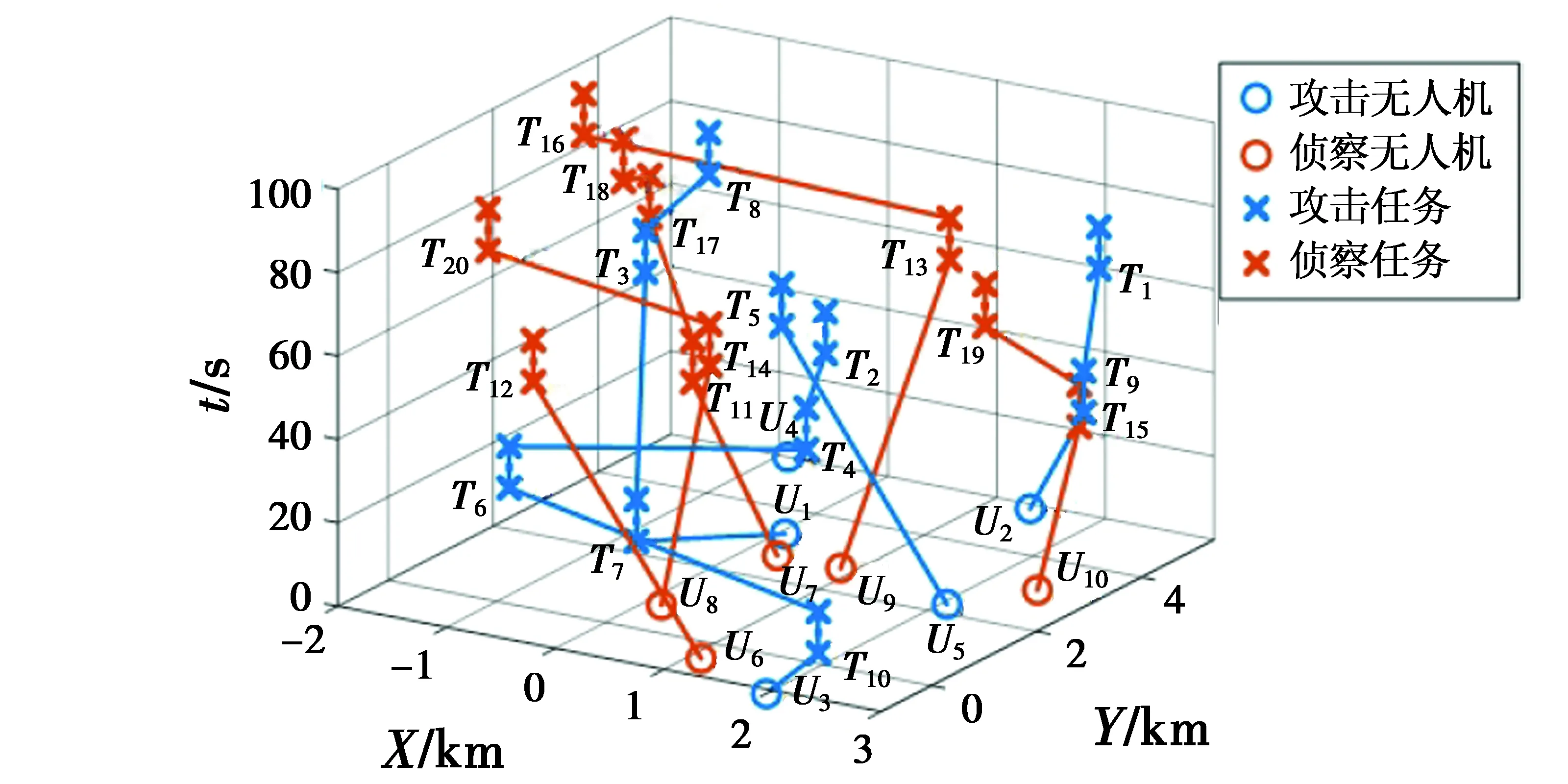

3.2 结果分析

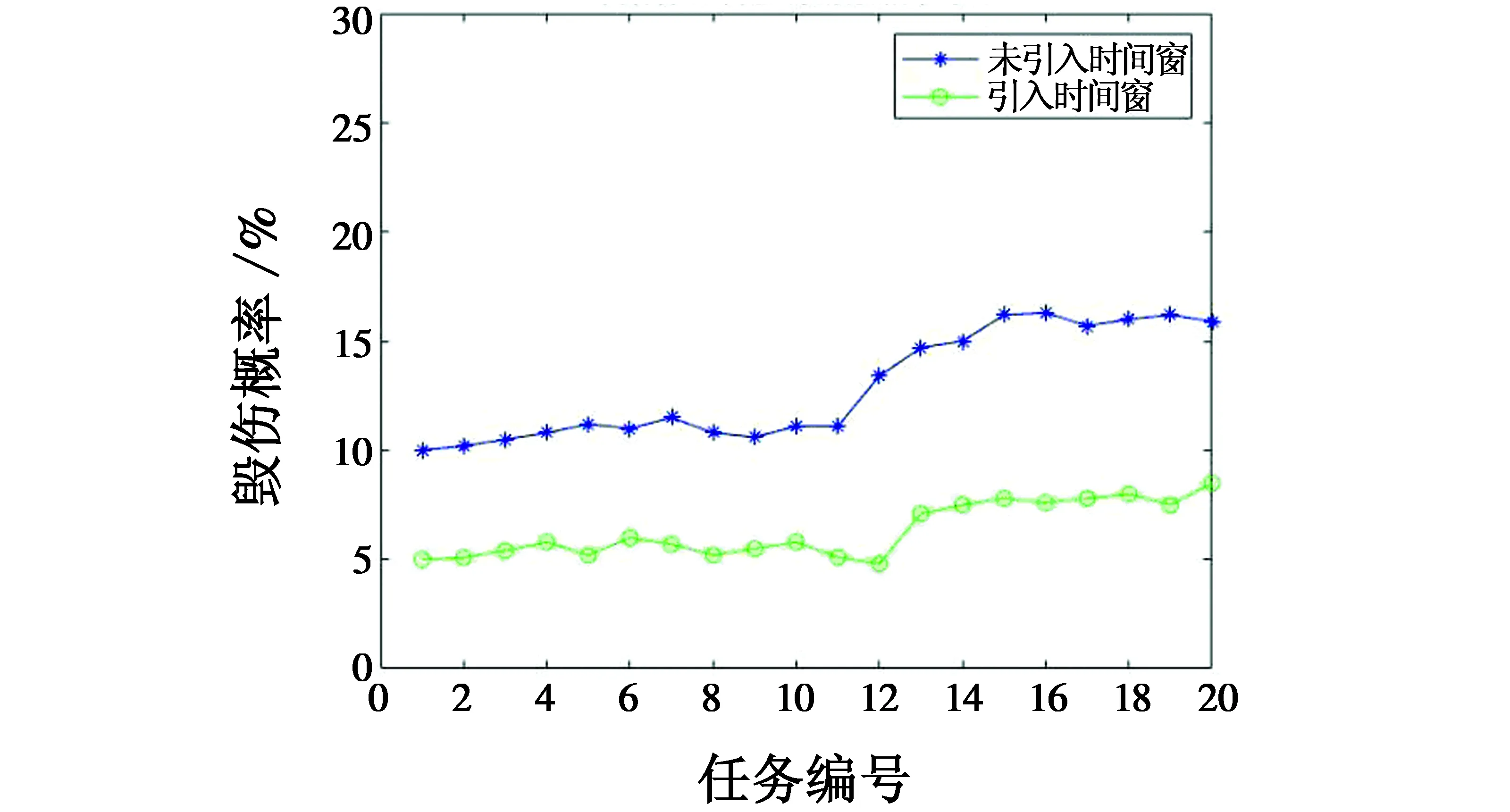
4 结论
