Sc、Ti、V、Zr 掺杂Cr2B3 高压力学性质的第一性原理计算

张 畅，孙小伟，宋 婷，田俊红，刘子江

（兰州交通大学数理学院, 甘肃 兰州 730070）

超硬材料是指维氏硬度大于40 GPa 的材料[1-2]。这些材料具有优异的性能，如高硬度、良好的导热性和不可压缩性、稳定的折射率和化学性质，广泛应用于工业和日常生活中，如磨料涂层、切割和抛光工具等[3-5]。2005 年，Kaner 等[6]提出，过渡金属具有较高的价电子密度和较强的不可压缩性，轻元素之间的共价键为结构提供了较高的剪切模量，过渡金属硼化物、碳化物和氮化物具有较高的硬度，甚至可能达到超硬材料的标准。铬硼化物是一种耐磨材料，人们从实验和理论上对其特性进行了广泛的研究[7-8]。铬硼化物中，通过实验证实其结构有CrB4、CrB2、Cr2B3、Cr3B4、CrB、Cr5B3和Cr2B[9-13]。其中，CrB4因其高硬度备受关注，例如：Niu 等[14]计算出空间群为Pnnm的CrB4的硬度为48 GPa，而后，Zhang 等[15]利用第一性原理方法系统地研究了CrB4的硬度随压力的变化规律。其余铬硼化物普遍具有较低的硬度[16-20]，限制了其工业应用。掺杂是一种提高材料硬度的行之有效的方法。Dovale-Farelo 等[21]采用第一性原理方法研究了不同浓度下Cr1-xMoxB2的机械性能，结果表明，CrB2的硬度为17 GPa，不满足硬质材料的标准，而Cr3MoB8、Cr2MoB6、CrMoB4、CrMo2B6和CrMo3B8的硬度均超过20 GPa，为硬质材料。在铬硼化物体系中，Cr2B3的力学性质仍缺少系统的理论计算。1985 年，Okada 等[22]通过高温Al-Cr-B 熔体制备了一种新型硼化铬晶体，即Cr2B3，随后采用单晶衍射法对Cr2B3的结构进行了研究[11]；1996 年，该团队发现Cr2B3结晶呈正交晶系，空间群为Cmcm，在(010)平面上测得的硬度为(22.4±1.7) GPa[17]。由此可见，Cr2B3的硬度仅达到硬质材料的标准。通过元素掺杂方式提高Cr2B3的硬度，将有助于拓展其工业应用范围。此外，在实际应用中，往往会遇到高压这一特殊工况。因此，研究掺杂Cr2B3在高压下的结构和力学性质尤为重要。

本工作首先将Cr2B3中的部分Cr 元素分别替换为Sc、Ti、V 和Zr 元素，考虑两种不同的替换方式，然后筛选出更优的替换位置；而后，利用第一性原理方法，计算掺杂结构的晶格常数、弹性常数、态密度、电子局域函数等；最后，基于电子结构讨论过渡金属元素Sc、Ti、V、Zr 的掺杂对Cr2B3维氏硬度和弹性模量的影响。

1 计算方法

采用密度泛函理论框架下的赝势平面波方法，运用CASTEP 软件包[23]对Cr2B3及其掺杂化合物的结构进行优化。实验中证实Cr2B3为正交晶系结构[22]，晶胞中共包含20 个原子，考虑50%的掺杂浓度，则其掺杂化合物的化学式可表示为CrMB3（M=Sc, Ti, V, Zr）。电子与电子之间的交换关联能采用Perdew 等[24]修正的PBESOL 形式的广义梯度近似（generalized gradient approximation，GGA），离子实与价电子之间的相互作用势用超软赝势描述[25]。Cr 原子和B 原子的电子组态分别为 3d54s1和2s22p1，掺杂原子 Sc、Ti、V 和 Zr 的电子组态分别为3d14s2、3d24s2、3d34s2和4d25s2。倒易空间布里渊区k点采用Monkhorst-Pack[26]方法选取，积分网格为14×2×14，平面波基函数的截断能量取为650 eV。迭代过程中系统能量的收敛标准为5×10-6eV/atom，作用在晶胞中每个原子上的力小于0.01 eV/Å，晶胞应力偏差低于0.02 GPa，最大位移的收敛公差小于5×10-4Å。

2 结果与讨论

2.1 结构稳定性

Cr2B3晶胞包含4 个Cr2B3单元，其空间群为Cmcm，晶格常数a= 3.026 4 Å，b= 18.115 0 Å，c= 2.954 2 Å。该结构共包含8 个Cr 原子、12 个B 原子，其中：Cr 原子有2 种占据方式，Cr1 和Cr2 占据的Wyckoff 位置分别为4c (0, 0.427 66, 0.25)和4c (0, -0.296 30, 0.25)；B 原子有3 种占据方式，即4c (0, 0.023 60, 0.25)、4c (0, 0.118 60, 0.25)和4c (0, -0.171 30, 0.25)，晶体结构如图1(a)所示。将该结构作为母体结构，对Cr2B3进行掺杂。用 Sc、Ti、V 和Zr 分别替换Cr2B3晶格中的Cr1 和Cr2，并对其进行几何优化，计算结果如表1 所示。除Sc 替换Cr2 位置外，其他替换情况下计算结果均可达收敛标准。Ti、V、Zr 掺杂元素替换Cr1 位置时具有更低的形成能和生成焓，由此可见，Cr1 位置为更优的替换位置。因此，将Cr2B3晶格中的Cr1 原子分别替换为过渡金属原子 Sc、Ti、V 和Zr，获得了掺杂结构CrMB3（M = Sc, Ti, V, Zr），如图1(b)所示。表1 也给出了优化后的晶格常数，与实验值[11]比较发现，二者之间的差异很小，表明本研究选取的计算参数是可靠的。同时，掺杂结构的空间群未发生变化。由此可知，原子的替换并未对Cr2B3的晶格结构产生明显的影响。

图1 (a) Cr2B3 和 (b) CrMB3（M = Sc, Ti, V, Zr）的晶体结构（蓝色、绿色和粉色小球分别代表 Cr、B 和过渡金属原子）Fig. 1 Crystal structures of (a) Cr2B3 and (b) CrMB3 (M=Sc, Ti, V, Zr), where the blue, green and pink spheres represent Cr, B and transition metal atoms, respectively

为研究掺杂元素对Cr2B3弹性性质的影响，首先要判断掺杂结构的稳定性。固体的结构稳定性可通过热力学稳定性、力学稳定性和动力学稳定性判断。

对于母体结构Cr2B3，其热力学稳定性可通过生成焓判断

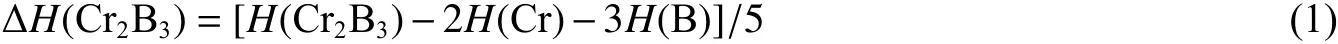
式中：ΔH(Cr2B3) 为化合物 Cr2B3的生成焓，H(Cr2B3)为Cr2B3的焓值，H(Cr)和H(B)分别为Cr 和B 作为单质存在的焓值。对于掺杂结构，则需要计算其形成能Ef[27]

式中：Ef为化合物 Cr2B3的形成能，E(CrMB3)为Cr2B3中掺杂Sc、Ti、V 和Zr 原子的总能量，E(Cr2B3)为Cr2B3的能量值，n为掺杂的原子数，µ为相应原子的化学势。 ΔH和Ef的计算结果也列于表1 中。可以看出，在零压下，Cr2B3的ΔH为负值，通过替换 Cr1 位置得到的掺杂结构CrMB3（M = Sc, Ti, V, Zr）的ΔH和Ef均为负值，表明它们都具备热力学稳定性。

表1 零压下Cr2B3 及掺杂结构CrMB3（M=Sc, Ti, V, Zr）的晶格常数、形成焓及掺杂结构的形成能Table 1 Lattice constants, formation enthalpy of Cr2B3 and CrMB3 (M = Sc, Ti, V, Zr), and impurity formation energy of CrMB3 (M=Sc, Ti, V, Zr) at zero pressure

本研究将通过计算上述结构的弹性常数来判断它们的力学稳定性。上述所有结构都属于正交晶系，该晶系具有9 个独立的弹性常数，即C11、C22、C33、C44、C55、C66、C12、C13和C23。根据Born 稳定性准则[28]，有

图2 和图3 给出了根据应力-应变关系计算得到的Cr2B3及其掺杂结构在不同压力下的弹性常数。上述所有结构在 0～150 GPa 的压力范围内均满足正交晶系的力学稳定性条件。将掺杂结构的弹性常数与 Cr2B3比较发现，V 掺杂可使Cr2B3的弹性常数C11、C22和C33均增大。C11、C22和C33是表征材料在a、b和c轴抗形变能力的参数，其值越大，抗形变能力越强。图2 显示，随着压力的升高，Cr2B3晶体在a、b和c轴上的抗形变能力逐渐增强。C44作为剪切弹性常数，其值越大，材料的剪切变形抗力越强。由图3 可知，CrTiB3和CrVB3的C44高于其他几种结构，这两种结构对应的剪切模量也高于其他几种结构，因此，CrTiB3和CrVB3具有更强的剪切变形抗力。

图3 CrMB3（M=Sc, Ti, V, Zr）的弹性常数随压力的变化Fig. 3 Pressure dependence of the elastic constants for CrMB3 (M=Sc, Ti, V, Zr)

为判断Cr2B3的动力学稳定性，通过有限位移法分别计算了Cr2B3在零压和150 GPa 高压下的声子色散曲线，如图4 所示。零压下，Cr2B3晶体的声子色散关系在整个布里渊区内未出现虚频，表明Cr2B3在零压下满足动力学稳定性；相比于零压，Cr2B3在150 GPa 下的声子色散曲线的频率有一定的提高，但其在X附近表现出虚频，因而动力学不稳定。图5 为CrScB3、CrTiB3、CrVB3和 CrZrB3在零压下的声子色散曲线，其中 CrVB3在G点出现微小虚频，CrScB3、CrTiB3和 CrZrB3出现了明显虚频，均不满足动力学稳定性。

图4 Cr2B3 在零压(a)和 150 GPa (b)下的声子色散曲线Fig. 4 Phonon-dispersion curves of Cr2B3 at (a) 0 GPa and (b) 150 GPa

2.2 弹性性质

根据弹性常数，可获得材料的体积弹性模量、剪切模量以及杨氏模量等力学参量。体积弹性模量B和剪切模量G采用Voigt-Reuss-Hill 近似法计算[29]， 杨氏模量E可由B和G推导得出，计算公式如下

式中：BV和BR为Voigt 和Reuss 模型的体积弹性模量，GV和GR分别为Voigt 剪切模量和Reuss 剪切模量。图6 为Cr2B3和CrMB3（M=Sc, Ti, V, Zr）的体积弹性模量、剪切模量和杨氏模量随压力的变化。可以看出，随着压力增加，Cr2B3及其掺杂结构的体积弹性模量、剪切模量、杨氏模量均增大。Cr2B3在整个压力范围内的体积弹性模量比其他4 种结构更大。相比于零压下的Cr2B3，零压下CrVB3和CrTiB3的剪切模量分别提高14.3%和16.2%，杨氏模量分别提高8.2%和12.0%。

图6 Cr2B3 和 CrMB3（M=Sc, Ti, V, Zr）的体积弹性模量(a)、剪切模量(b)和杨氏模量(c)随压力的变化Fig. 6 Pressure dependence of (a) the bulk moduli, (b) the shear moduli, (c) the Young’s moduli for Cr2B3 and CrMB3 (M=Sc, Ti, V, Zr)

硬度是材料抵抗永久变形能力的量度，是材料的重要力学参数。Cr2B3及其掺杂结构的理论维氏硬度采用半经验模型[30]计算

图7 为 Cr2B3及其掺杂结构的维氏硬度随压力的变化曲线。可以看出，在研究的整个压力范围内，除压力超120 GPa 的Zr 掺杂外，Sc、Ti、V 和Zr 元素的掺杂均使Cr2B3的维氏硬度有所提高。值得注意的是，Ti 掺杂使Cr2B3的硬度从26.3 GPa 提高至40.2 GPa，提高52.9%，达到超硬材料的标准。随着压力的增加，Cr2B3的硬度呈线性增加，但其硬度仍较低，150 GPa 下仅为28.3 GPa，CrZrB3的硬度总体呈下降趋势， CrVB3的硬度在37 GPa 上下小幅波动，而CrScB3和CrTiB3的硬度随着压力的增加发生明显的波动。在CrScB3的硬度随压力的变化曲线中，100 GPa 时出现明显的波动，计算得到该点的形成能Ef为0.083 295 eV，为正值，不满足热力学稳定性，因此出现了力学性质异常。CrTiB3在零压下的维氏硬度明显高于其他压力下的硬度，达到超硬材料的标准，且在整个压力范围内，CrTiB3的硬度始终高于另外4 种结构。总体看来，CrVB3同时具备较高的硬度以及较小的压力依赖性，是理想的硬质材料。

Cr2B3的硬度随压力变化呈现出明显的规律性，因此针对Cr2B3在不同压力下的B-B 键的键长及布居数做进一步计算，结果如表2 所示。通常，键长越短，材料的硬度越高。表2 显示，随着压力的升高，Cr2B3的3 类B-B 键，即B1-B1、B1-B2 和B2-B3 的键长均缩短。此外，还可通过布居数判断B-B 共价键强弱（通常，正值表示共价键，正值越大，共价性越强），进而分析硬度随压力变化的原因。Cr2B3的B-B 键的布居数随压力升高均增大，表明B-B 键的共价性随压力的升高而增强，与Cr2B3的硬度随压力的变化趋势一致。

表2 Cr2B3 中B-B 键的键长以及布居数随压力的变化Table 2 Pressure dependence of B-B bond length and population for Cr2B3

过渡金属元素的掺杂虽提高了Cr2B3的硬度，但同时使材料的韧性有所降低。根据Pugh 规则[31]，可以判断出固体的韧脆性。一般说来，当B/G小于1.75 时，材料表现出脆性，反之则表现出韧性。图8给出了Cr2B3和CrMB3（M=Sc, Ti, V, Zr）的B/G随压力的变化。零压下，Cr2B3及其掺杂结构的B/G均小于1.75，表现出脆性，而掺杂结构的B/G比Cr2B3的更小，表现出更明显的脆性；Cr2B3和CrZrB3分别在65.0 和93.7 GPa 由脆性转变为韧性。

图8 Cr2B3 及 CrMB3（M=Sc, Ti, V, Zr）的B/G 随压力的变化Fig. 8 Pressure dependence of the B/G for Cr2B3 and CrMB3(M=Sc, Ti, V, Zr)

图9、图10、图11 和图12 为零压下Cr2B3及其掺杂结构的体积弹性模量和杨氏模量在xy、xz和yz面的投影图。在yz平面上，Cr2B3及其掺杂结构的体积弹性模量的二维投影近似为圆形，表明材料的体积弹性模量在yz平面上呈各向同性；在xy平面和xz平面上，Cr2B3及其掺杂结构的体积弹性模量和杨氏模量的二维投影偏离圆形，表明材料的体积弹性模量和杨氏模量在xy和xz平面上呈各向异性。掺杂结构与Cr2B3的体积弹性模量大致相同，说明掺杂对体积弹性模量的各向异性没有明显的影响。CrTiB3和CrVB3的杨氏模量在xz平面上的投影相比于Cr2B3仅出现微小变化，说明在xz平面上V 和Ti 元素的掺杂对杨氏模量各向异性的影响较小。

图9 零压下 Cr2B3 的体积弹性模量的三维表示(a)及其在 xy、xz 和 yz 面上的投影(b)Fig. 9 (a) 3D representation and (b) 2D projections on xy, xz and yz planes of the bulk modulus for Cr2B3 at 0 GPa

图10 零压下 Cr2B3 的杨氏模量的三维表示(a)及其在 xy、xz 和 yz 面上的投影(b)Fig. 10 (a) 3D representation and (b) 2D projections on xy, xz and yz planes of the Young’s modulus for Cr2B3 at 0 GPa

图11 零压下 CrMB3（M=Sc, Ti, V, Zr）的体积弹性模量在 xy、xz 和 yz 面的投影Fig. 11 2D projections of the bulk modulus for CrMB3 (M=Sc, Ti, V, Zr) on xy, xz and yz planes at 0 GPa

图12 零压下 CrMB3（M=Sc, Ti, V, Zr）的杨氏模量在 xy，xz 和 yz 面的投影Fig. 12 2D projections of the Young’s modulus for CrMB3 (M=Sc, Ti, V, Zr) on xy, xz and yz planes at 0 GPa

2.3 电子结构

电荷密度和态密度（density of states，DOS）可以用于揭示结构的电子性质。计算了零压下 Cr2B3及其掺杂结构的总态密度和分波态密度，如图13 和图14 所示，其中虚线所处位置为费米能级。在费米能级上，各结构的态密度值均大于零，表明所有结构都具有明显的金属性。通过态密度分析可以看出：对于Cr2B3，在-5.0～-3.4 eV 区间，B-2p 和Cr-3d 具有相似形状的峰，出现杂化现象，说明Cr 原子与B 原子之间的化学键存在共价键成分，而在8.9～12.3 eV 区间，B-2p 与B-2s 发生了强烈的杂化，使得Cr2B3具有较高的硬度；对于CrScB3，在2.3～3.2 eV 区间，B-2p 与Cr-3d 发生杂化；对于CrTiB3，在-3.8～-2.5 eV 区间，B-2p 与Ti-3d 发生杂化；对于CrVB3，在-4.4～-3.0 eV 区间，V-3d 与B-2p 发生杂化；对于CrZrB3，在-3.4～-2.3 eV和1.5～3.0 eV 区间，B-2p 与Cr-3d 以及Zr-4d 出现了形状相似的峰，说明此处出现杂化现象。

图13 零压下 Cr2B3 的总态密度以及分波态密度Fig. 13 Total density of states and partial density of states for Cr2B3 at 0 GPa

图14 零压下 CrMB3（M=Sc, Ti, V, Zr）的总态密度以及分波态密度Fig. 14 Total density of states and partial density of states for CrMB3 (M=Sc, Ti, V, Zr) at 0 GPa

金属与非金属之间的B―M 共价键有利于提高剪切模量，形成的M―M 金属键将降低材料的剪切模量。为了揭示化学键合的性质与维氏硬度的关系，计算了Cr2B3和CrMB3（M=Sc, Ti, V, Zr）的电子局域函数（electronic local functions，ELF）[32]，并选取了(100)平面和( 0 01)平面进行分析，结果如图15 所示。图15 中电荷高度局域位置用红色显示，表明该处存在强的共价键。对比Cr2B3及其掺杂结构在(100)面上的电荷局域分布情况，可以看出掺杂结构B-B 之间的红色区域相较于Cr2B3均有所扩大。在( 0 01)晶面上，Cr2B3的电荷主要集中在B-B 之间的连线上，而掺杂结构的B 原子被红色区域包围，代表着电子集中在B 原子的周围。材料的硬度往往与B-B 共价键的强弱相关。掺杂结构具有更强的B-B共价键，因而拥有更高的硬度。

图15 零压下(a) Cr2B3、(b) CrScB3、(c) CrTiB3、(d) CrVB3、(e) CrZrB3 在(100)平面的 ELF 以及零压下(f) Cr2B3、(g) CrScB3、(h) CrTiB3、(i) CrVB3 和(j) CrZrB3 在( 001)平面的 ELFFig. 15 Electronic local functions contours for (a) Cr2B3, (b) CrScB3, (c) CrTiB3, (d) CrVB3 and (e) CrZrB3 in plane(100) at 0 GPa, and electronic local functions contours for (f) Cr2B3, (g) CrScB3, (h) CrTiB3,(i) CrVB3 and (j) CrZrB3 in plane ( 001) at 0 GPa

3 结 论

利用第一性原理方法，对Cr2B3的生成焓，CrMB3（M=Sc, Ti, V, Zr）的形成能，以及他们的弹性常数、弹性模量和电子结构进行了详细的计算和讨论。结果表明，在零压下 Sc、Ti、V 和 Zr 元素的掺杂均使Cr2B3的维氏硬度有所提高。其中，CrTiB3的硬度达到40.2 GPa，为潜在的超硬材料。在 0～150 GPa压力范围内，Cr2B3、CrVB3和CrZrB3的硬度随压力的变化趋势呈现一定的规律性：Cr2B3的硬度随压力的增加而单调增加；CrVB3的硬度受压力的影响很小，且相较于Cr2B3具有更高的硬度；CrZrB3的硬度随压力的增加，总体呈下降趋势。Cr2B3的B-B 键长随压力增大而缩短，同时布居数增大，表明Cr2B3的B-B 共价键增强，导致Cr2B3的硬度随压力的增加而增大。