抗侵彻孔结构装甲的可靠性优化设计
2022-08-10姚晨辉李安祺
姚晨辉,杨 刚,张 哲,李安祺
(湖南大学机械与运载工程学院特种装备先进设计技术与仿真教育部重点实验室, 湖南 长沙 410082)
孔结构装甲是兼顾抗侵彻性能和轻量化设计的防护装甲之一。通过在实心装甲上设计一定形状、一定尺寸和一定分布方式的孔洞,装甲可具备独特的结构效应,能对入射子弹产生有效的消蚀和偏转,从而在满足抗侵彻需求的同时有效降低装甲重量[1-2]。由于孔结构装甲所具有的优点,不少学者对孔结构装甲进行了抗侵彻机理和结构设计的研究。Chocron 等[1]研究了在侵彻孔结构装甲过程中子弹的侵蚀机理,指出子弹与孔边缘发生碰撞时受到的不对称力作用导致弹体侵蚀或者断裂。Kiliç等[3]阐述了孔结构装甲抗侵彻机理,主要包括弹道偏转、弹体断裂和弹芯侵蚀3 种形式。Mishra 等[4]研究了开孔的形状和尺寸对孔结构装甲抗弹性能的影响。Radisavljevic 等[5]研究了不同的弹芯直径与孔径尺寸比下孔结构装甲的毁伤机理和抗弹性能。王郑[6]研究了间隙对穿孔装甲抗弹性能的影响,表明在一定设计范围内,增大间隙可提高孔结构装甲的抗弹性能。王建波等[7]研究了不同弹着点对孔结构装甲的防护性能的影响。胡丽萍等[8]采用残余穿深法对孔结构装甲的抗弹性能进行了评估分析。秦庆华等[9]基于数值仿真,探讨了不同弹目交汇条件下孔结构装甲的抗侵彻性能。肖红亮等[10]研究了不同弹丸类型作用下,倾角效应对孔结构装甲抗弹性能的影响。李换芝[11]采用数值仿真分析了弹体旋转及靶板倾角等对孔结构装甲抗弹性能的影响。彭吉祥等[12]设计了斜孔结构装甲,并基于数值模型分析了其抗弹性能及规律。Burian 等[13]通过实验和数值模拟,研究了不同孔径尺寸和间隙尺寸下孔结构装甲的抗弹性能及机理。此外,还有学者在孔结构装甲材料选型方面开展了相关研究。Cui 等[14]采用一种由非晶合金涂层和孔结构金属基板组成的非晶合金增强穿孔装甲,并研究了该装甲的弹道极限和失效机理。
由上述分析得知,当前的已有研究主要集中在孔结构装甲抗侵彻机理及规律的探讨,孔结构装甲的尺寸设计主要是在机理分析的基础上由经验或枚举式分析确定。孔结构装甲在满足抗侵彻性能的前提下,其孔径和间隙尺寸是否可以进一步优化,到目前为止尚未见从优化设计理论的角度开展相关研究报道。此外,在孔结构装甲的制造与实际应用中存在诸多不确定因素,例如子弹侵彻的弹着点、入射速度、入射角以及装甲孔系的结构尺寸等。这些不确定因素会直接影响孔结构装甲抗侵彻性能的可靠性。因此,对孔结构装甲进行轻量化及可靠性设计时,除满足一定的抗侵彻性能条件外,还需考虑关键不确定因素的影响。
本研究以孔结构装甲的轻量化设计为目标,探讨适用于孔结构装甲的可靠性优化设计方法。结合已有的孔结构抗侵彻机理的分析研究[1,3],以孔结构装甲的最薄弱抗弹工况为设计原型,通过可靠性优化设计对孔结构装甲进行减重。由于是在与原型抗弹性能一致的最薄弱抗弹工况下进行可靠性优化设计,因此设计后的孔结构装甲在其他工况下的抗弹性能可得到保障。
1 孔结构装甲可靠性优化设计的整体流程框架
孔结构装甲可靠性优化设计流程如图1 所示。采用代理模型构建孔结构装甲的抗侵彻性能的功能函数。为了保证代理模型在抗侵彻性能方面的样本的准确性和有效性,通过ANSYS 软件进行弹体侵彻孔结构装甲的仿真模型建立与验证,并在此基础上对ANSYS 软件进行二次开发,实现弹体侵彻孔结构装甲的参数化建模和样本数据提取。在有效的侵彻响应数据的基础上,应用Kriging代理模型构建方法完成孔结构装甲抗侵彻响应代理模型的建立。代理模型可有效表征弹目交汇条件、孔结构装甲特征尺寸等因素与抗侵彻响应之间的关系。最后,在考虑孔结构装甲尺寸、弹体入射速度、入射角度均具有一定不确定性的情况下,通过序列优化与可靠性评估方法(sequential optimization and reliability assessment, SORA)实现孔结构装甲的可靠性优化设计。
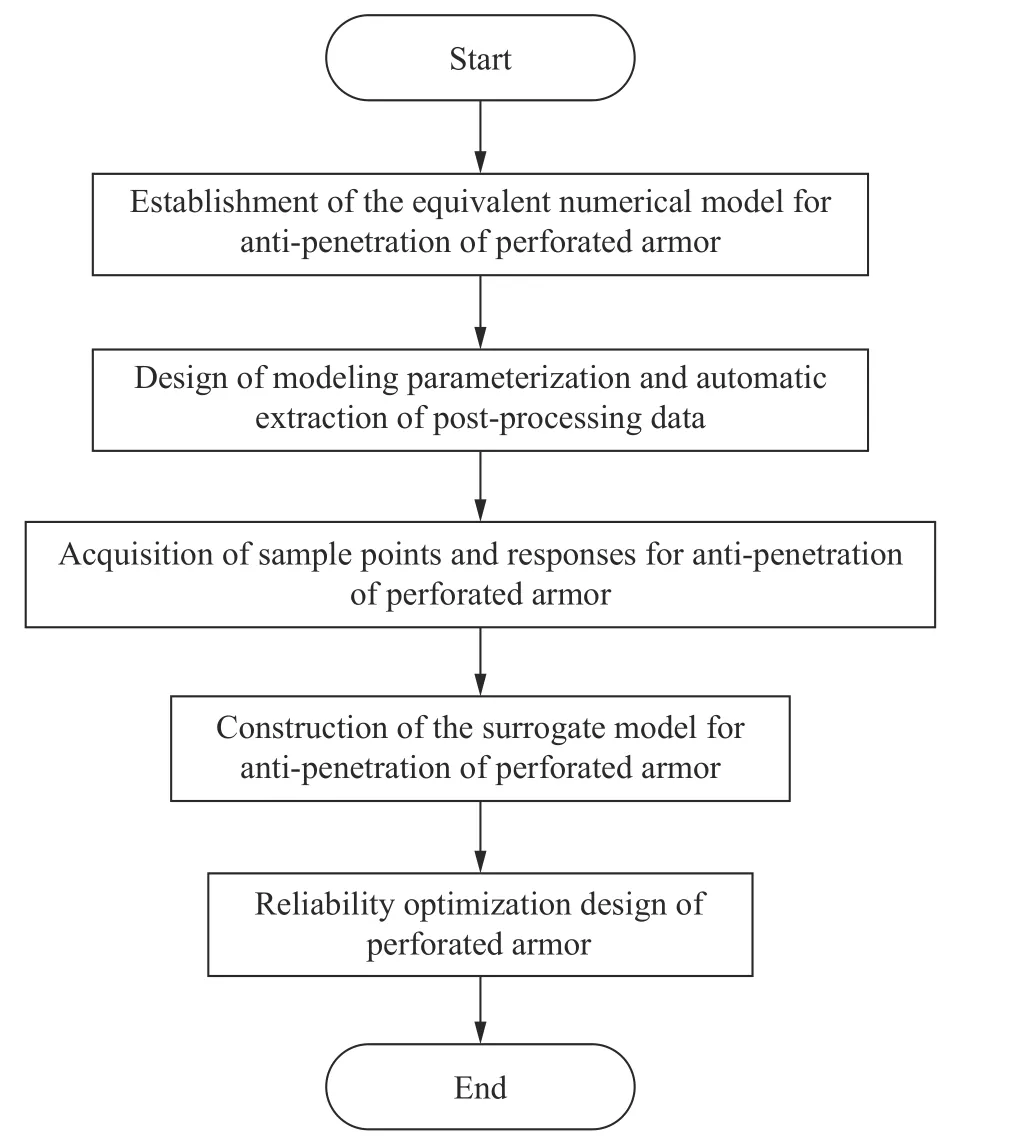
图1 孔结构装甲可靠性优化设计流程Fig. 1 Flow chart of reliability optimization design for perforated armor
2 数值模型的建立与有效性验证
孔结构装甲可靠性优化设计需要大量的样本数据,但实弹侵彻的成本高昂,因此需借助有效的数值模型获得样本数据。本研究建立的弹体侵彻孔结构装甲模型以Kiliç等[3]的实验研究为依据。
子弹侵彻孔结构装甲的数值模型如图2 所示。孔结构装甲和后效实心装甲的材料均为Secure 500 钢,且均为四周固定约束。子弹为7.62X54R 穿甲弹,以854 m/s 的初始速度垂直入射孔结构装甲,弹着点分别为两孔中心连线的中点(见图2(b)中弹着点Ⅰ)和3 孔中心连线构成的三角形中心(见图2(b)中弹着点Ⅱ)。
根据文献[3]中孔结构装甲的尺寸设计,孔结构装甲上的圆形孔以等距交错的形式分布,其中孔直径为6 mm,孔间距为10 mm,如图2(b)所示。为了提高数值模型的计算效率,仅在弹体与装甲有接触影响的有效尺寸范围内构建等效孔结构装甲模型。等效孔结构装甲数值模型的长为54 mm;宽为50 mm;厚度与实际模型一致,为6 mm。采用扫掠网格方法对孔结构装甲进行网格划分,在弹体与装甲接触区域进行网格细化处理以提高仿真结果的准确性,如图2(b)所示,其中网格单元尺寸为0.5 mm。后效实心装甲的网格采用相同方法和相近尺寸进行划分。
实际7.62X54R 穿甲弹由黄铜外壳、尖端填充剂、淬硬钢芯、尾端填充剂、弹底板等组成。考虑到填充剂的质量较轻,在侵彻过程中对装甲的毁伤作用相对弹芯、弹底板和外壳可忽略不计,因此在子弹数值模型的建立过程中仅考虑弹芯、弹底板和外壳。其中弹体的外径为7.8 mm,芯径为6.2 mm,芯长为28.2 mm,弹头呈椭圆状,整个弹体的总重约为10 g。数值模型建立过程中,弹体各部分采用扫掠网格生成方法划分,网格单元尺寸为0.3 mm,如图2(c)所示。

图2 子弹侵彻孔结构装甲的数值模型Fig. 2 Numerical model of bullet penetration into perforated armor
采用显式动力分析有限元软件LS-DYNA 进行数值模拟,弹体和装甲均选用Johnson-Cook 本构模型[15]和Grüneisen 状态方程描述,其中Johnson-Cook 本构模型为
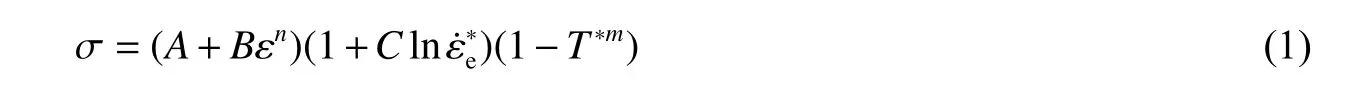
式中: σ为等效应力;A为 屈服应力;B为硬化模量; ε为等效塑性应变;n为硬化系数;C为应变率敏感系数; ε˙∗e= ε˙/ε˙0为 无量纲应变率,其中, ε˙0为 参考应变率, ε˙为 应变率;T∗为 无量纲温度,T∗=(T−T0)/(Tm−T0),其中T0为 室温,Tm为 材料熔化温度;m为温度敏感性系数。
数值模型中弹体外壳、弹芯和装甲等选用的材料的具体参数见表1[3],其中ρ 为密度,E为弹性模量,G为剪切模量,v为泊松比,cp为比定压热容。

表1 弹体与装甲材料参数[3]Table 1 Material parameters of bullet and armor[3]
数值模型的有效性验证是通过将数值仿真计算获得的孔结构装甲毁伤特征与实验结果对比实现的。子弹侵彻孔结构装甲的数值仿真结果与实验结果的对比分别如图3 和图4 所示。图3 为弹着点Ⅰ、Ⅱ处孔结构装甲毁伤的数值仿真结果与实验结果对比。由图3 可以看出,孔结构装甲毁伤的数值仿真结果与实验结果基本吻合。图4 给出了数值仿真和实验得到的子弹贯穿孔结构装甲后后效实心装甲产生的损伤结果,其中数值仿真获得的弹着点Ⅰ、Ⅱ处后效装甲产生的损伤深度D的平均值为1.75 mm,文献[3]给出的多次实验不同弹着点的平均损伤深度D为1.8 mm。孔结构装甲毁伤形貌的数值仿真结果与实验结果一致,并且后效实心装甲损伤深度的数值仿真结果与实验结果相近,说明所建的数值模型有效。

图3 子弹侵彻后孔结构装甲毁伤的仿真结果与实验结果[3]对比Fig. 3 Comparison of the simulation and the experimental[3] results of the damage in the perforated armor after the bullet penetration

图4 实心装甲损伤的数值仿真结果与实验结果[3]对比Fig. 4 Comparison of the numerical simulation and the experimental[3] results of the damage in the solid armor
3 孔结构装甲抗侵彻响应代理模型建立
为满足高效采样和可靠性优化设计的需求,在孔结构装甲可靠性优化时需构建孔结构装甲抗侵彻性能的功能函数。工程结构可靠性优化的常规处理方法一般是通过代理模型建立结构响应功能函数[16]。因此,本研究拟通过分析有限次数的数值仿真结果,建立包含孔结构装甲的结构特征尺寸参数、弹目交汇条件参数与孔结构装甲抗侵彻响应关键参数间相互关系的代理模型。
根据已有文献对孔结构装甲抗侵彻机理的分析[7-8],弹着点在孔中心时孔结构装甲的抗侵彻性能最弱,因此在考虑不确定性情况下的孔结构装甲轻量化设计时,为保障抗侵彻性能,选用弹着点为孔中心的最弱工况进行可靠性优化设计。代理模型中孔结构装甲的抗侵彻性能采用弹体侵彻孔结构装甲后弹芯的剩余速度v′和剩余质量m′进行表征。
孔结构装甲抗侵彻响应代理模型的构建流程如图5 所示。首先利用最优拉丁超立方法生成一定数目的初始样本集,并通过子弹侵彻装甲数值模型的参数化流程自动获取样本集对应的响应集。然后根据样本集和响应集,利用Kriging 代理模型方法建立孔结构装甲的抗侵彻代理模型,并利用平均绝对误差及最大绝对误差准则,判断抗侵彻代理模型是否满足一定的精度要求。如果不满足精度要求,则利用期望改变量(expected improvement, EI)加点法在设计空间域内拟合精度较差的区域进行样本点补充;如果满足精度要求,则终止加点,获得孔结构装甲的抗侵彻性能函数。最后,根据设计要求,将孔结构装甲的抗侵彻性能函数作为可靠性优化的约束条件。
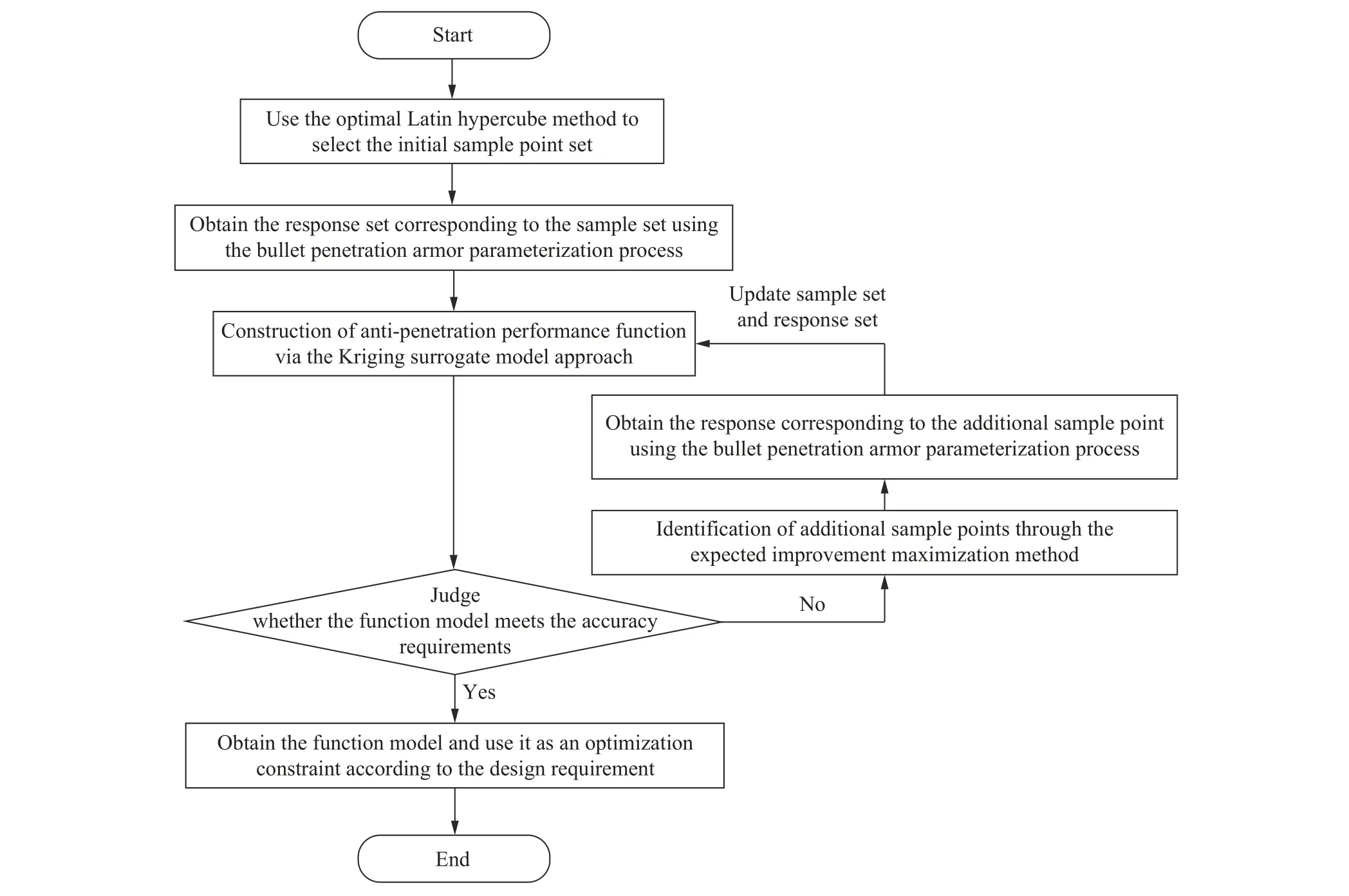
图5 孔结构装甲抗侵彻性能函数代理模型构建流程Fig. 5 Flow chart of the construction process of surrogate model for anti-penetration performance function of perforated armor
3.1 代理模型与参数化建模
孔结构装甲抗侵彻性能代理模型的构建需通过数值模型仿真分析获得数据样本。通常情况下,在代理模型的构建过程中,设计变量及响应的样本点需进行实时选取分析。为减少每次采样时人为重建孔结构装甲抗侵彻的有限元模型所耗费的时间成本,本研究在确立孔结构装甲抗侵彻的可靠性优化原型模型后,通过参数化建模的方法实现不同采样工况下有限元模型的自主构建与计算分析。
由于孔结构装甲的抗侵彻性能采用弹芯的剩余速度和剩余质量进行表征,因此在代理模型的构建过程中,对于抗侵彻孔结构装甲原型,不考虑后效实心装甲,如图6 所示。代理模型中,主要设计参数为孔结构装甲的孔直径和孔间距,主要的输入变量为子弹的入射速度和入射角度。
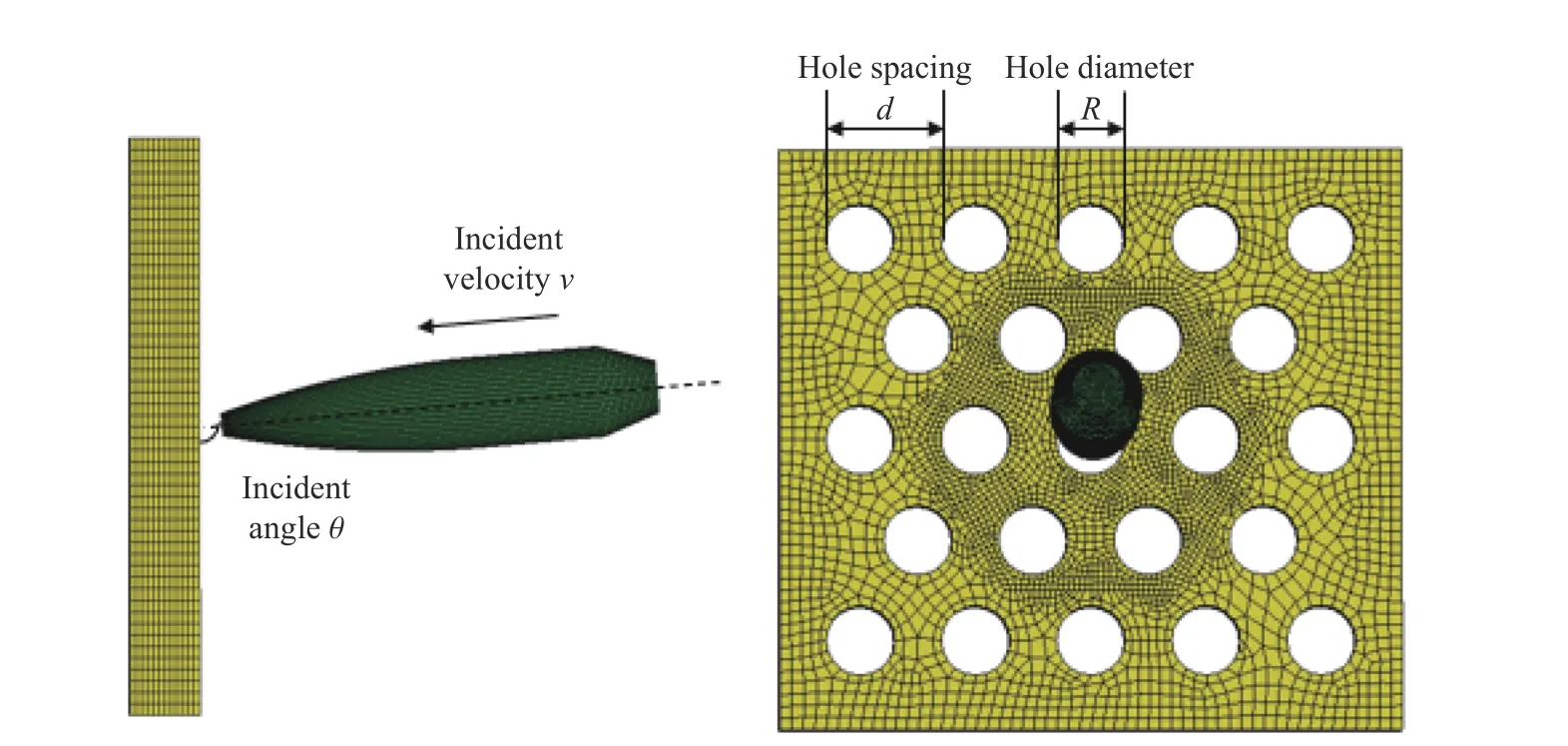
图6 抗侵彻孔结构装甲的原型Fig. 6 Numerical model of the prototype of the anti-penetration perforated structure armor
确立孔结构装甲抗侵彻原型的数值模型后,采用ANSYS/LS-DYNA 动力学仿真软件进行参数化建模[17],参数化建模与数据提取流程如图7 所示。参数化建模采样嵌套在代理模型的构建过程中,因此需实现代码的程序化,本研究采用MATLAB 来实现。参数化建模计算与数据提取的过程是以代理模型构建的样本为输入,然后结合ANSYS 的APDL 参数化建模命令流完成子弹侵彻装甲数值模型的前处理阶段,随后进入求解阶段进行计算分析,计算完成后将生成的D3PLOT 文件导入LSPREPOST 进行后处理,通过相关宏命令程序完成输出响应变量的提取过程。实现孔结构装甲抗侵彻的参数化建模后,在整个代理模型的构建过程中可根据需求自行实现建模分析和采样,不再需要人为干预,可有效提高代理模型的构建效率。
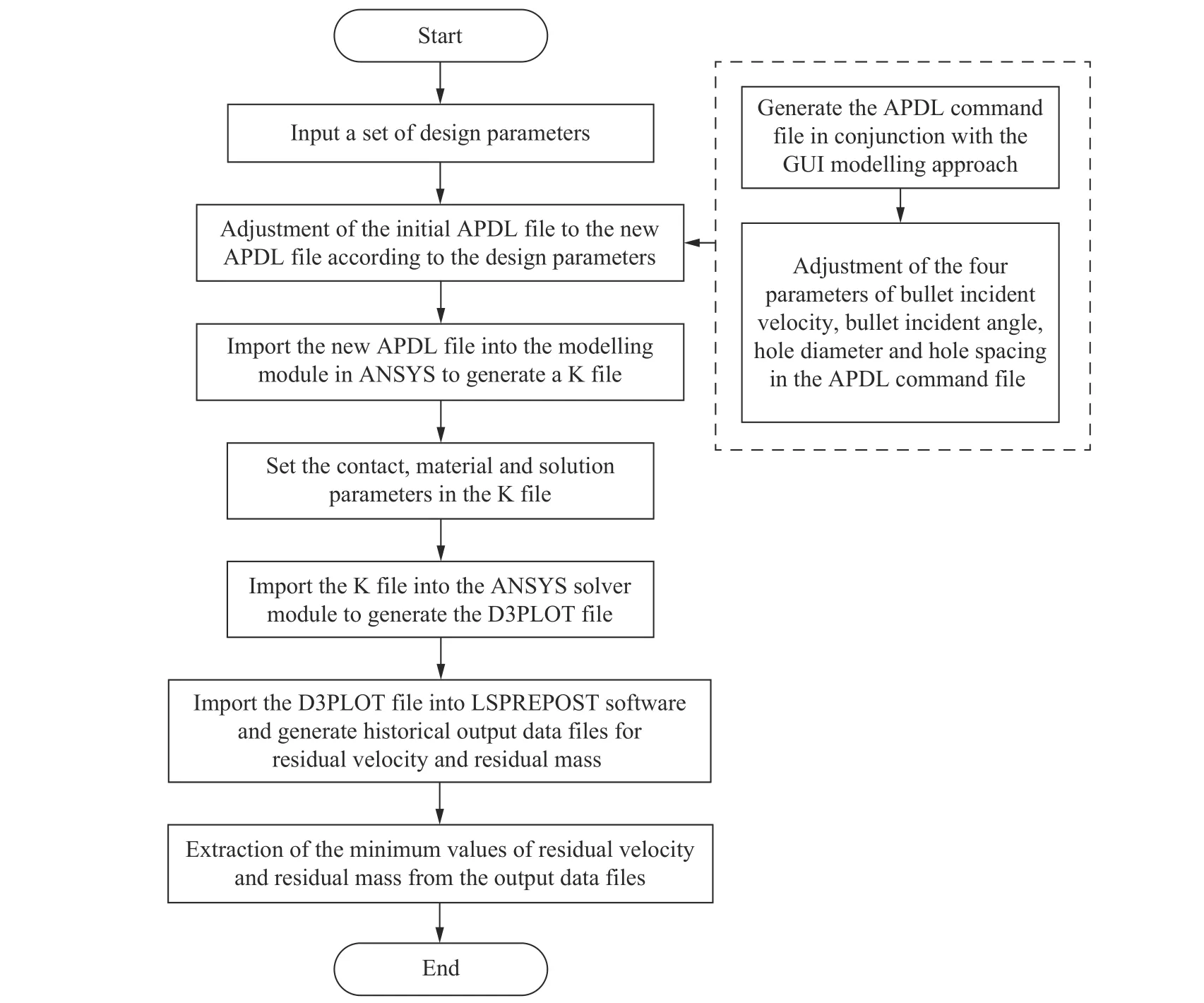
图7 孔结构装甲抗侵彻分析的参数化流程Fig. 7 Flow chart of parameterized process of anti-penetration analysis of perforated armor
3.2 Kriging 代理模型构建方法及EI 加点法


3.3 孔结构装甲代理模型
根据孔结构装甲可靠性优化设计需求,本研究在构建孔结构装甲抗侵彻响应代理模型时考虑的结构尺寸变量和弹目交汇变量包括孔直径R、 孔间距d、子弹入射速度v、子弹入射角 θ等。输出响应为子弹侵彻孔结构装甲后弹芯的剩余速度和剩余质量。根据已有的相关文献[21]对孔结构装甲机理与规律的研究及相关装甲防护设计3 级防护标准要求[22],代理模型设计中相关变量的约束范围列于表2 中。

表2 孔结构装甲可靠性优化设计相关变量的约束范围Table 2 Ranges of the relevant variables in reliability optimization design of perforated structure armor
按照表2 中给出的相关变量的约束范围,采用Space-Filling 抽样结合补充抽样的方法选取总样本点集。首先,利用最优拉丁超立方方法抽取一定组数的初始样本点,并利用弹体侵彻孔结构装甲参数化流程获取初始样本点集对应的响应集;然后,通过对这些样本点拟合构建的代理模型进行精度校核,判断得到的代理模型是否满足精度要求;最后,根据校核结果决定是否采用EI 加点准则补充样本点数,一般情况下,补充的样本点数不宜过多,避免出现过拟合现象,以保证代理模型具有较好的整体和局部拟合精度。
根据研究问题的拟合精度需求,本研究在Space-Filling 取样环节中利用最优拉丁超立方法抽取24 组样本点(如表3 所示)拟合代理模型,并利用EI 加点准则,基于24 组拟合结果和不同响应输出分析分别增加6 组样本点(分别如表4、表5 所示),其中各变量及响应的数值均保留3 位有效数字。
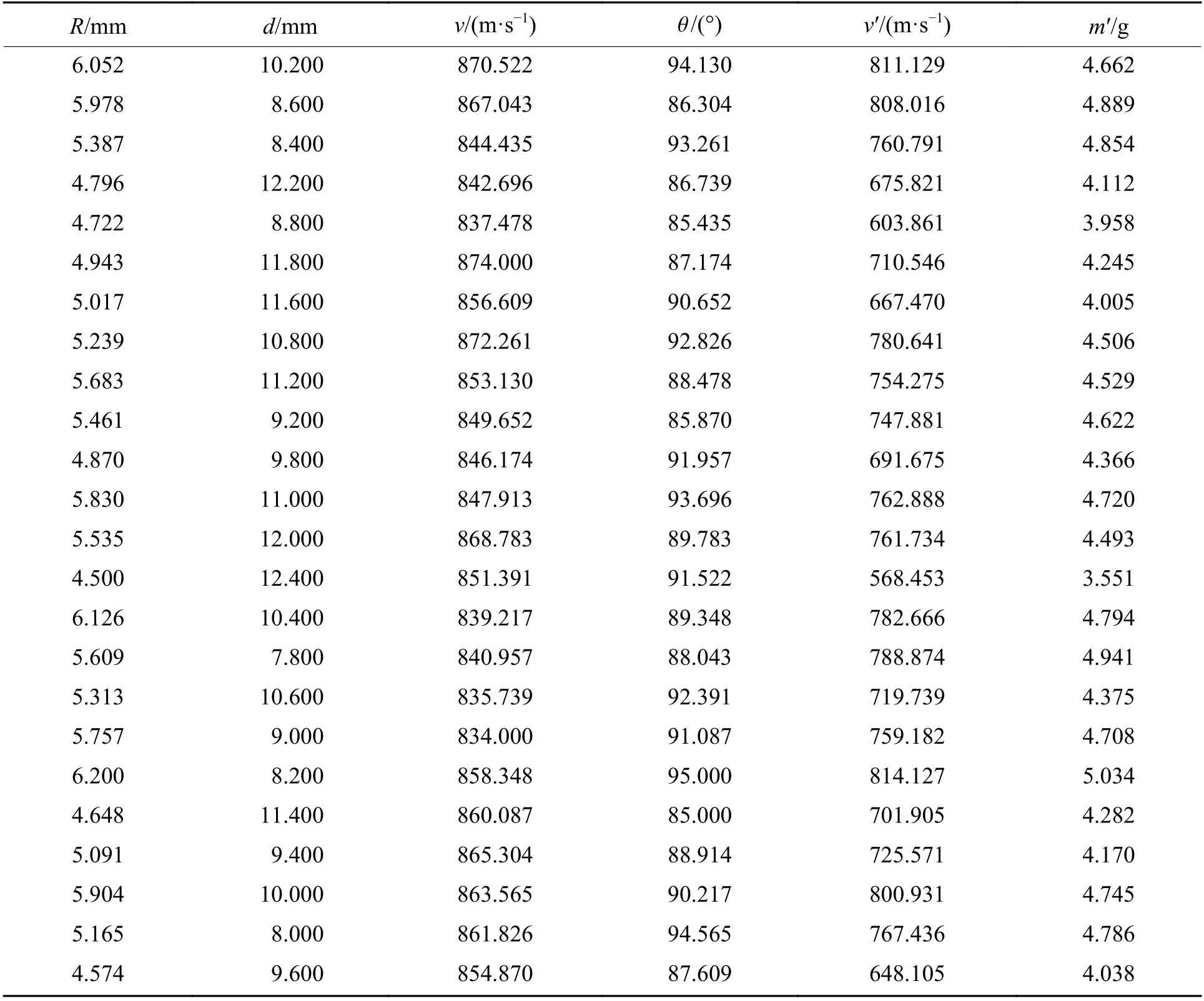
表3 最优拉丁超立方法抽取的采样点和响应Table 3 Sampling points and responses obtained by the optimal Latin hypercube method
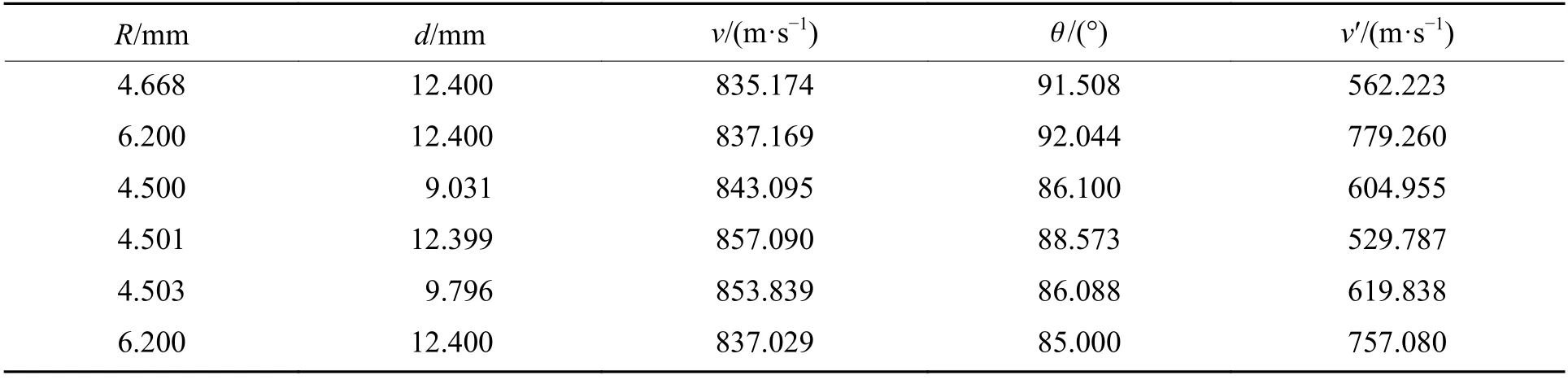
表4 剩余速度响应代理模型构建的新增样本和响应Table 4 Added samples and responses built by residual velocity response surrogate model
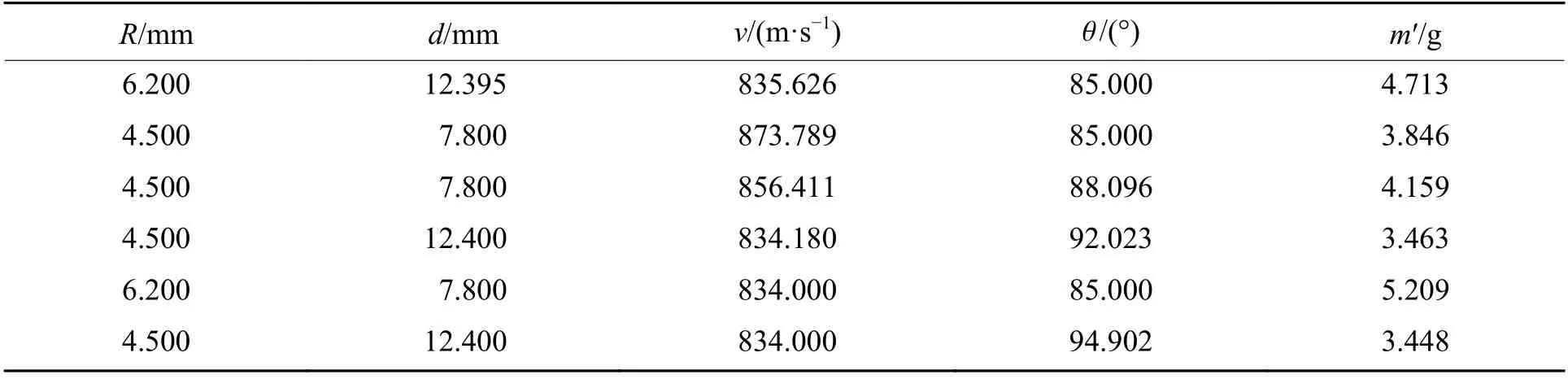
表5 剩余质量响应代理模型构建的新增样本和响应Table 5 Added samples and responses built by residual mass response surrogate model


式中:AAE为平均绝对误差,MAE为最大绝对误差,n为 校核样本点的数目,yi和yˆi分别为校核样本点的真实值和代理模型的预测值。校核样本点和结果如表6 所示。
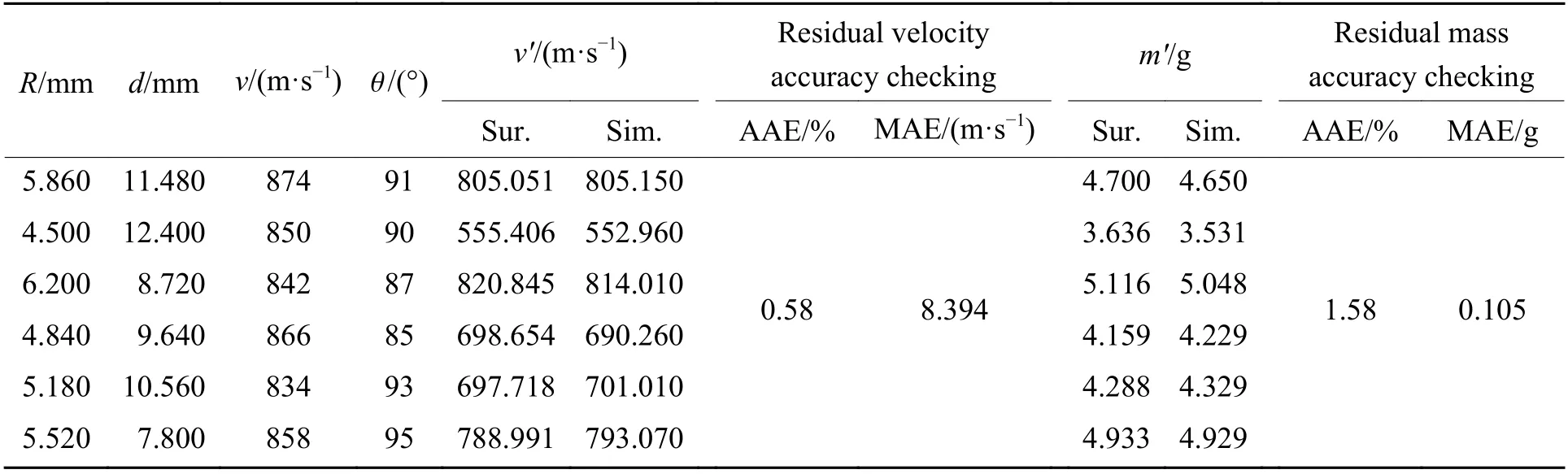
表6 校核样本点和结果Table 6 Check samples and results
选定的总样本点构建的代理模型的校核结果显示,速度响应代理模型的AAE 为0.58%,MAE 为8.394 m/s,质量响应代理模型的AAE 为1.58%,MAE 为0.105 g。因此,所构建的剩余速度和剩余质量的代理模型均具有较好的整体精度和局部精度,可作为孔结构装甲可靠性优化的约束条件。
4 孔结构装甲可靠性优化设计
孔结构装甲可靠性优化设计时,以孔结构装甲的轻量化为设计目标,抗侵彻性能的功能函数为约束条件,弹体入射速度、入射角度为随机性参数,孔数为确定性设计变量。此外,为了对孔结构装甲进行充分的可靠性优化设计,以孔系的孔直径、孔间距为随机性设计变量,并假定孔系中所有孔的尺寸均符合相同的随机性特征。
本研究采用的可靠性优化方法为序列优化与可靠性评估(SORA)方法。SORA 方法是一种经典的解耦方法[23-26],该方法的主要思想是通过构造移动矢量,使概率性约束转化为等效的确定性约束,从而将可靠性优化流程分解为可靠性分析和确定性优化的迭代过程。该方法可避免传统可靠性方法将可靠性分析嵌套于设计优化环节的不便,具有较高的求解精度和求解效率。结合SORA 方法,孔结构装甲可靠性优化设计流程如图8 所示。
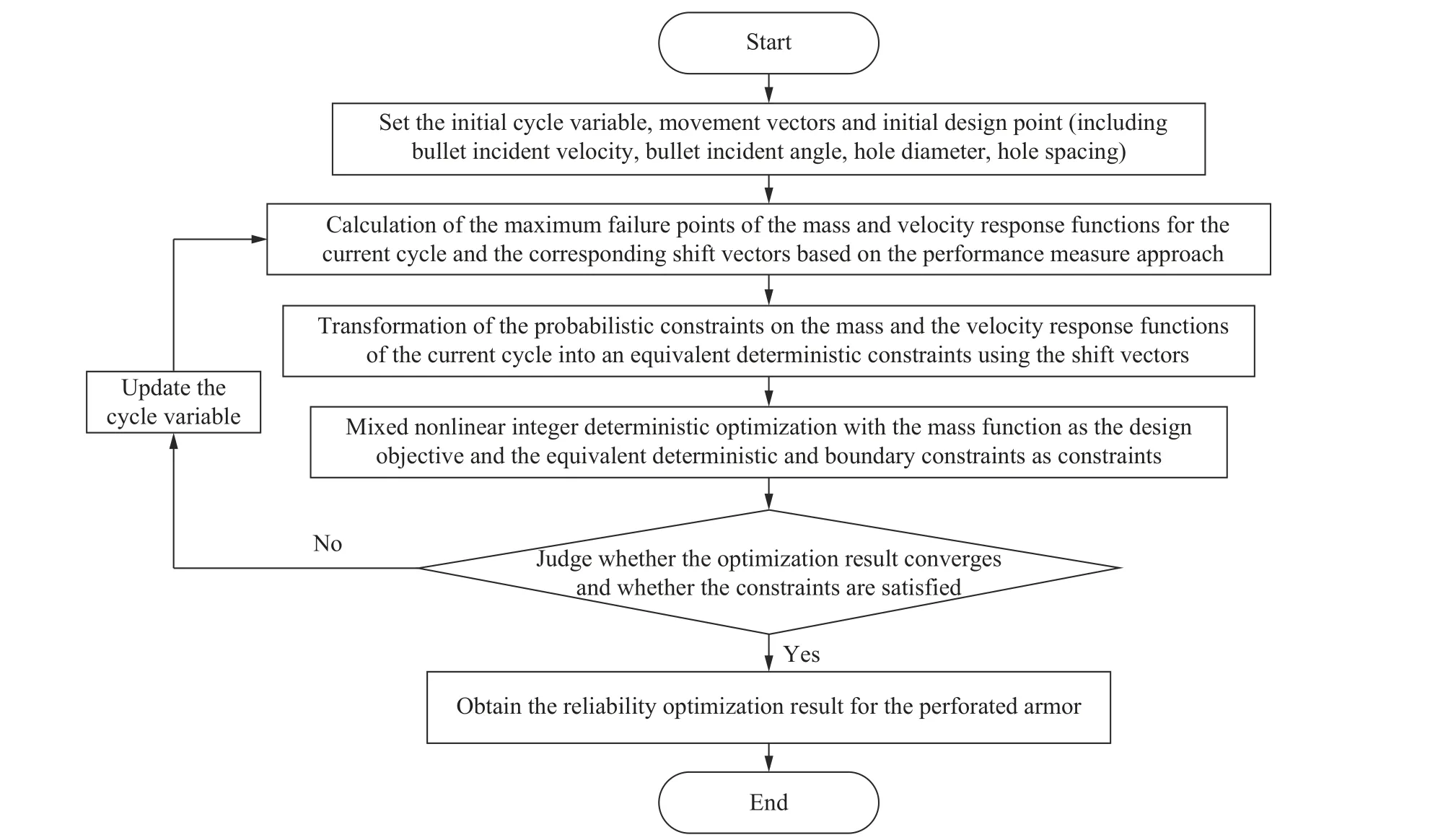
图8 孔结构装甲可靠性优化流程Fig. 8 Flow chart of reliability optimization process of perforated armor
首先,设定初始循环变量、移动矢量和初始设计点。其次,基于功能度量法分别计算当前循环的剩余速度性能函数和剩余速度性能函数的最大失效点及对应的移动矢量,并利用移动矢量将当前循环的概率性约束等效为确定性约束。然后,以孔结构装甲的质量函数最小化为设计目标,等效确定性约束为约束条件,进行确定性优化,另外由于本研究中孔结构装甲的确定性设计变量孔数为整型变量,故确定性优化方法为混合非线性整数优化。最后,判断优化是否收敛以及约束条件是否满足要求,如果不满足就更新循环变量,进入下一个循环,直至优化收敛并且约束条件得到满足,从而获得孔结构装甲可靠性优化结果。
4.1 可靠性优化数学模型
本研究以孔直径R、 孔间距d为随机性设计变量,弹体入射速度v、入射角度 θ为随机性参数,孔数为确定性设计变量。按照工程上的一般假设,设定各个随机变量和参数在设计空间内均服从正态分布且变异系数取0.02。以长100 mm、宽100 mm、高6 mm 的孔结构装甲为设计典型。此外,由于孔系中圆孔为三角状交错分布,且孔直径和孔间距属于设计变量,导致装甲的孔数不易于采用单一变量进行表达,因而研究中设定2 个变量联合表征,即孔结构装甲长度方向上(每行)可容纳的最大孔数n1和宽度方向上(每列)可容纳的最大孔数n2。各随机变量参数的概率分布信息如表7 所示。

表7 随机变量参数的概率分布信息Table 7 Probability distribution information of random variables and parameters
考虑到孔结构装甲的质量函数与孔数密切相关,且用以表征孔数的函数由于边界约束为多段函数,因此孔结构装甲的质量函数也采用多段函数的形式描述,具体如式(12)中的M′所示。研究以弹芯的剩余速度功能函数和剩余质量功能函数为优化的概率性约束条件,并取约束上限为确定性优化结果中的剩余速度768.512 m/s 和剩余质量4.686 g。结合工程实际应用的一般要求,取概率性约束的可靠度为0.9,即同一批次的孔结构装甲在给定的约束条件和工况下,有90%的装甲满足抗侵彻性能要求。此外,根据孔结构装甲孔系设计的分布特征与几何约束,优化过程中引入相关几何约束条件,如式(12)的g3、g4、g5、g6所示。最终,构建的孔结构装甲可靠性优化模型为
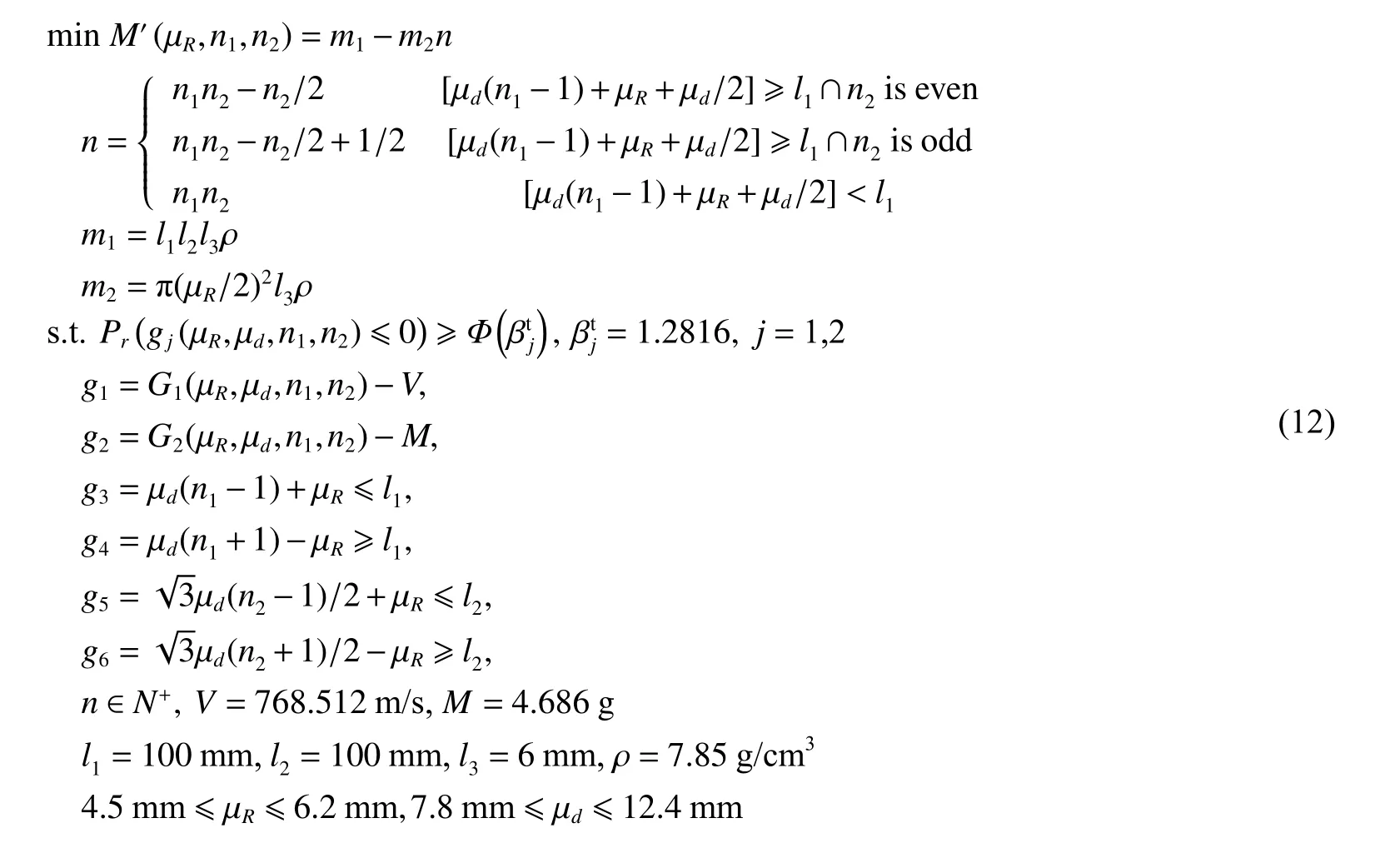


4.2 优化结果分析和验证
通过可靠性优化后得到的孔结构装甲的优化参数结果如表8 所示,其中,孔直径和孔间距的数值结合工程实际保留2 位有效数字。由表8 可知,在可靠度为0.9 的要求下进行可靠性优化后,孔结构装甲的孔直径由6.00 mm 减小为5.06 mm,孔间距由10.00 mm 减小为7.83 mm,而装甲上的总孔数呈现增加趋势。

表8 孔结构装甲优化参数结果Table 8 Parameter results of the optimization of perforated structure armor
为了验证可靠性优化的效果,在入射角度为90°、入射速度为854 m/s 的条件下,将孔结构装甲的优化参数代入数值模型进行分析计算,可得优化前后的输出响应以及装甲的质量属性,如表9 所示。优化前后孔结构装甲的结构如图9 所示。

表9 输出响应和孔结构装甲质量属性Table 9 Output responses and the quality attributes of perforated structure armor
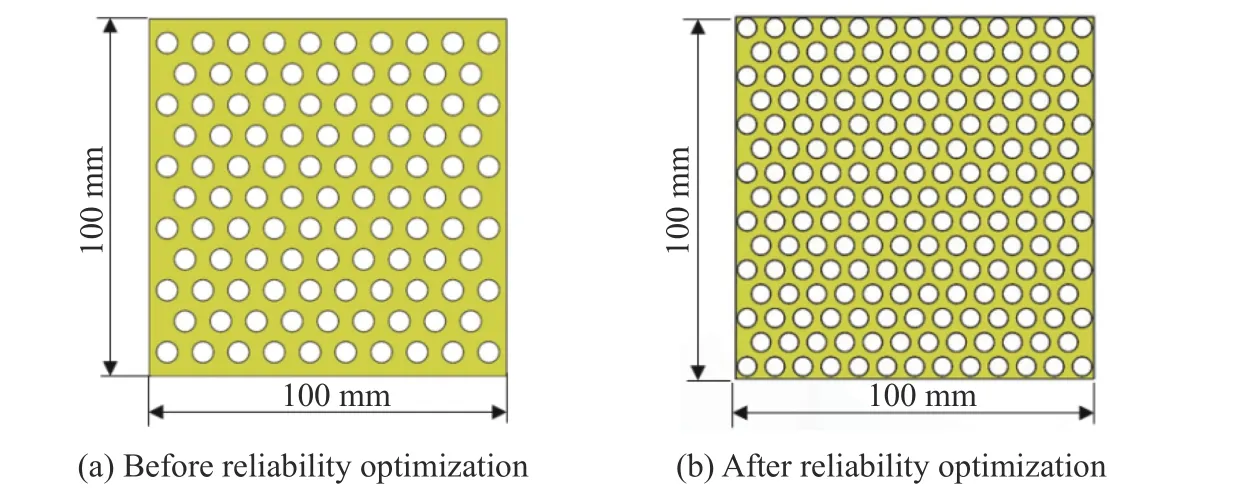
图9 可靠性优化设计前后的孔结构装甲Fig. 9 Perforated armor before and after reliability optimization
由表9 可知,经过可靠度为0.9 的可靠性优化后,在同样的外界条件下,剩余速度响应和剩余质量响应与初始设计相比略有下降,孔结构装甲的面密度下降至2.93 g/cm2,与初始设计相比降低了11.5%。可见,孔结构装甲经可靠性优化设计后质量显著减轻,并且相应工况下的防护性能也得到一定提升。
5 结 论
针对孔结构装甲开展了考虑不确定性情况下的轻量化设计,首先建立弹体侵彻孔结构装甲的数值模型,并进行参数化建模,然后通过代理模型构建孔结构装甲抗侵彻性能的功能函数,最后进行孔结构装甲的可靠性优化。可得以下结论:
(1) 在抗侵彻孔结构装甲的可靠性优化设计时,参数化建模技术方法的引入可实现样本和响应数据的高效采集,相关的方法及流程易拓展到其他抗侵彻结构的设计;
(2) Space-Filling 抽样与补充抽样方法相结合可在确保代理模型精度的前提下减少代理模型构造过程中所需的样本点数量;
(3) 针对本研究的工况类型,在可靠度为0.9 的要求下孔结构装甲可靠性优化设计结果显示,孔结构装甲的面密度由3.31 g/cm2下降至2.93 g/cm2,比初始设计降低11.5%,轻量化效果显著。
本研究以抗侵彻孔结构装甲为典型研究对象开展的可靠性优化设计方法可为其他抗侵彻防护结构的可靠性优化设计提供设计参考。
