压装连接对加速度计层间信号粘连的影响

邱云潇，何丽灵,2，陈 刚,2，吴 昊，李继承,2

（1. 中国工程物理研究院总体工程研究所, 四川 绵阳 621999；2. 西南科技大学工程材料与结构冲击振动四川省重点实验室, 四川 绵阳 621010；3. 同济大学土木工程学院, 上海 200092）

引信控制技术是战斗部研制的关键技术之一[1]。计层起爆作为引信起爆控制方式之一，其关键技术是利用加速度计测量的信号判断弹体着靶、出靶，实现计层[2]。穿过多层间隔靶时，若加速度计测量的信号出现粘连[3-4]，将无法识别层间及穿靶过程，从而导致计层错误。支撑引信决策的加速度信号是通过特定的加速度测量装置（简称“装置”）获得的。装置可采用多种方式与弹体相连，如螺纹连接、压装连接、法兰连接等[5-9]。不同连接界面必然引入不同类型的几何间断，改变装置的结构动态响应。这可能加剧装置内加速度计测量的层间加速度信号的粘连，导致信号不能准确反映弹体的加速度响应[5,9]。

为实现连接结构与理想刚性连接的近似，一方面，工程实践中采用辅助手段，如压装连接中引入初始安装预紧等，削弱连接界面对装置结构动力学响应的消极影响。准静态的经验公式可判定初始预紧装配时连接结构的强度[10]。然而，在侵彻类高过载动态加载时，无经验公式预判预紧压装对弹体及装置的结构动力学响应的影响，且缺乏动态加载下压装连接与理想刚性连接近似的判定准则。此外，当压装连接与理想刚性连接偏离时，压装连接对加速度层间信号粘连的影响也缺乏研究。另一方面，基于经典振动理论将加速度计测量信号分解为弹体刚体过载与弹体结构振动的加速度[11-12]。但理论分析中假设装置与弹体间为理想刚性连接，未考虑几何间断可能引入的间隙碰撞等附加影响。

本研究将主要依托数值仿真，针对多层靶侵彻问题，研究压装连接时装置与弹体间隙的动态变化；基于频域响应建立压装连接与理想刚性连接近似的判定方法；讨论压装连接时可能影响加速度信号粘连的因素。研究结论将为压装连接时层间信号粘连的机理识别与控制奠定基础。

1 侵彻引入的压装连接几何间断特征的动态变化与控制

1.1 数值仿真模型校核

本研究依托的弹体及靶标与文献[13]中的工况3-2 一致。弹体为头部尖卵形的圆柱，弹头曲径比为3，形状及尺寸见图1，装置与弹体压装连接。数值仿真模型见图2。试验中弹体以597 m/s 速度垂直侵彻靶标。靶标为两块675 mm×675 mm 钢筋混凝土板，前板厚200 mm，后板厚100 mm，间距270 mm[13]。试验前，尾盖将装置压装在弹舱中，并施加适当预紧。分析模型中将尾盖与弹体的螺纹连接简化为理想刚性连接，即连接面共节点处理。

图1 含加速度测试装置的试验弹[13]Fig. 1 Projectile containing accelerometer equipment[13]

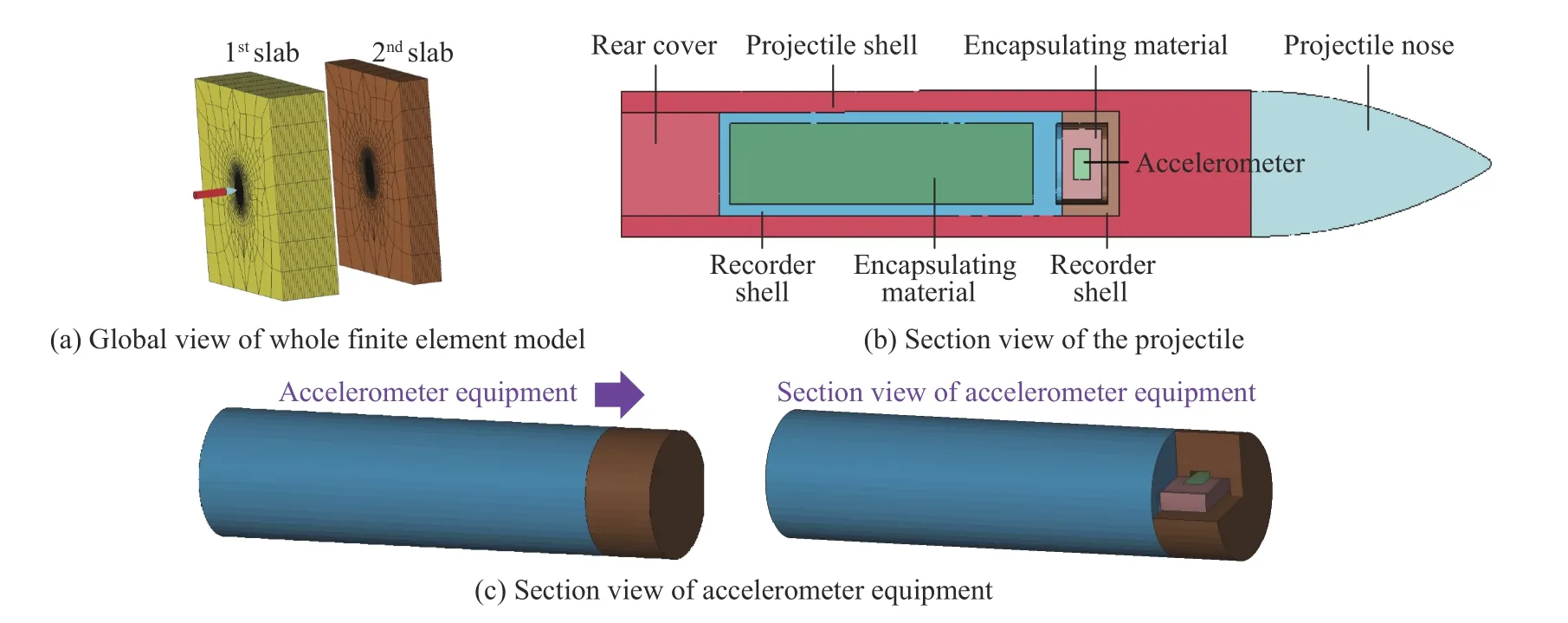
图2 数值仿真模型Fig. 2 Finite element model for numerical simulation

弹体外壳与尾盖为45CrNiMoV 钢，装置外壳为TC4 钛合金，数值仿真时均采用Johnson-Cook 模型描述其力学性能。灌封材料和靶板的力学性能分别采用双线性弹塑性本构模型和HJC 模型描述。弹靶本构模型参数见表1、表2 和表3[14-17]，其中：ρ 为密度，G为剪切模量，ν 为泊松比，Tm为熔化温度，cp为比定容热容，A为参考应变率及参考温度下的初始屈服强度，B和n为材料的应变硬化参数，C为材料应变率强化参数，m为材料的热软化参数，D1～D5为损伤模型中的材料参数，σy为屈服强度，Etan为正切模量，fs为失效应变，a为归一化黏聚强度参数，b为压力硬化系数，c为应变率系数，N为压力硬化指数，Smax为最大特征化等效应力，fc为准静态单轴抗压强度，T为拉伸强度，EFMIN为材料断裂时的最小塑性应变，pcrush为弹性极限压力，Ucrush为pcrush下的弹性极限体积应变，plock为压实静水压力，Uplock为对应于plock的体积应变，K1、K2、K3为压力常数。

表1 弹体外壳、尾盖与测试装置外壳的材料参数[14–15]Table 1 Material parameters for shell and rear cover of projectile and shell of accelerometer equipment[14–15]

表2 灌封材料参数[16]Table 2 Material parameters for encapsulating compound[16]

表3 靶板材料参数[17]Table 3 Material parameters for target[17]

图3 展示了数值仿真得到的弹体运动参数与试验结果的对比。图3 显示，弹体的加速度最大值和剩余速度的数值仿真结果分别为6.4×104g和274 m/s，试验测试结果（滤波后）分别为6.7×104g和247 m/s，二者的相对偏差分别为4.5%和-11.0%，积分后位移的相对偏差在5%以内。数值仿真与试验结果较为一致，验证了数值仿真模型的合理性。

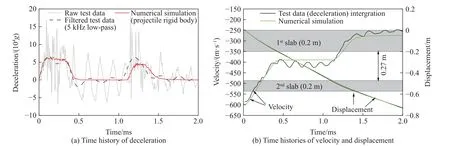
图3 弹体运动学参数试验结果与数值仿真结果对比Fig. 3 Comparison of kinematic parameters of projectile obtained by experimental measurement and numerical simulation

1.2 侵彻多层靶时装置与弹体间隙的动态变化与控制

装置的典型压装连接方式见图4，加速度计安装在装置中，其中δAB与δCD为装置端面与弹体外壳端面中心点间的距离。鉴于加速度计尺寸相对较小，且其采用螺接、胶粘与灌封等相结合的方式与装置连接，本研究将二者的连接关系简化为理想刚性连接。若装置与弹体为理想刚性连接，则侵彻过程中及侵彻后均应满足δAB≡δCD≡0。对于实际压装结构，初始装配时δAB=δCD=0。

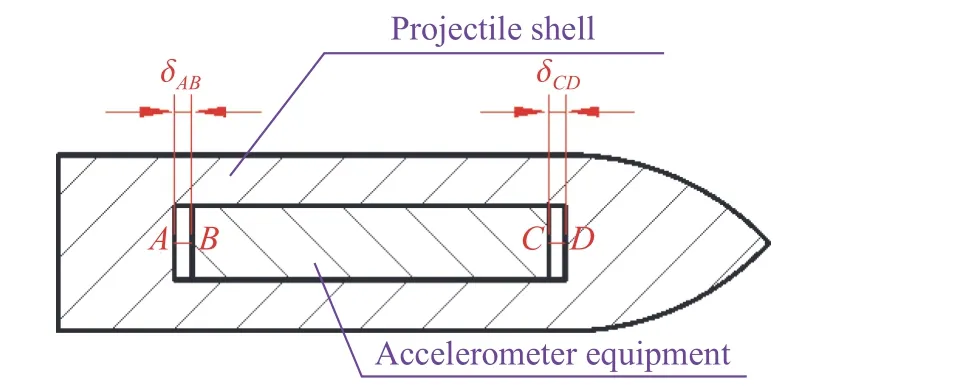
图4 装置在弹体内安装的示意图Fig. 4 Schematic diagram of pressed connection between projectile and accelerometer equipment

为分析预紧压装连接对弹体结构动态响应的影响，以理想刚性连接以及无预紧压装为参考工况，在4 种预紧压装连接工况下（预紧力分别为1.0、2.2、5.3 和10.3 kN）开展了弹体以597 m/s 的速度正侵彻双层靶的数值仿真。工况设计见表4。

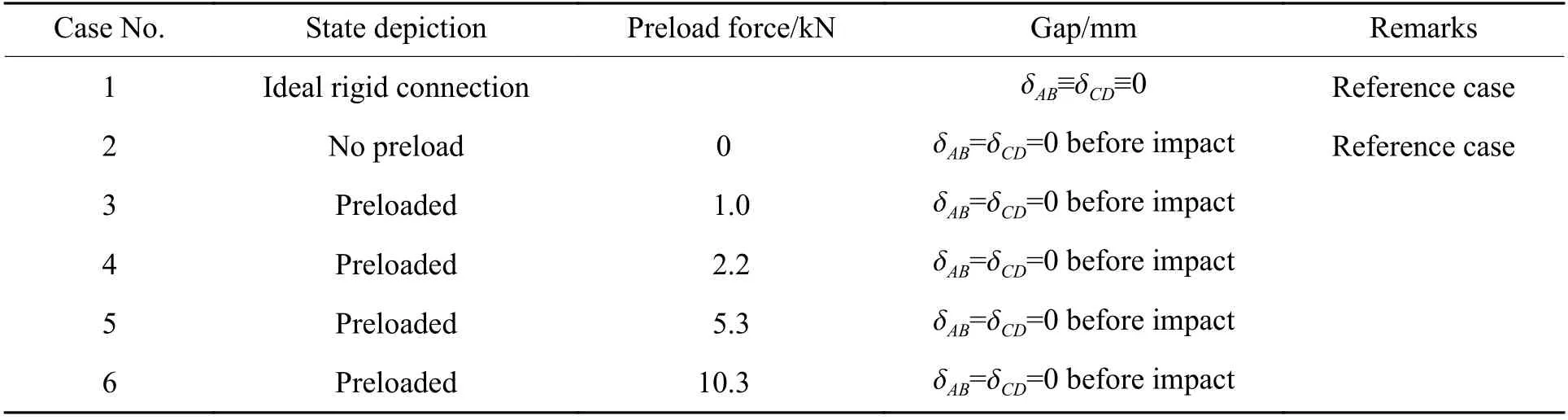
表4 弹体以597 m/s 正侵彻的数值仿真工况设计Table 4 Different conditions of numerical simulations for normal impact at projectile velocity of 597 m/s

图5 显示了表4 中工况2～工况6 下装置与弹仓的间隙δAB和δCD的动态变化。由图5 可知，在弹体与靶板的相互作用阶段，δCD约为0 µm，δAB>0 µm。在此阶段，初始安装预紧对装置与弹仓间隙变化的影响较小。在层间及靶后飞行阶段，整弹无外载作用。无预紧压装时，δAB>0 µm 与δCD>0 µm交替出现。当预紧力为5.3 与10.3 kN 时，δAB和δCD被抑制，并趋近于0 µm。因此，存在可抑制层间间隙的最小预紧力，其值在2.2～5.3 kN 之间。

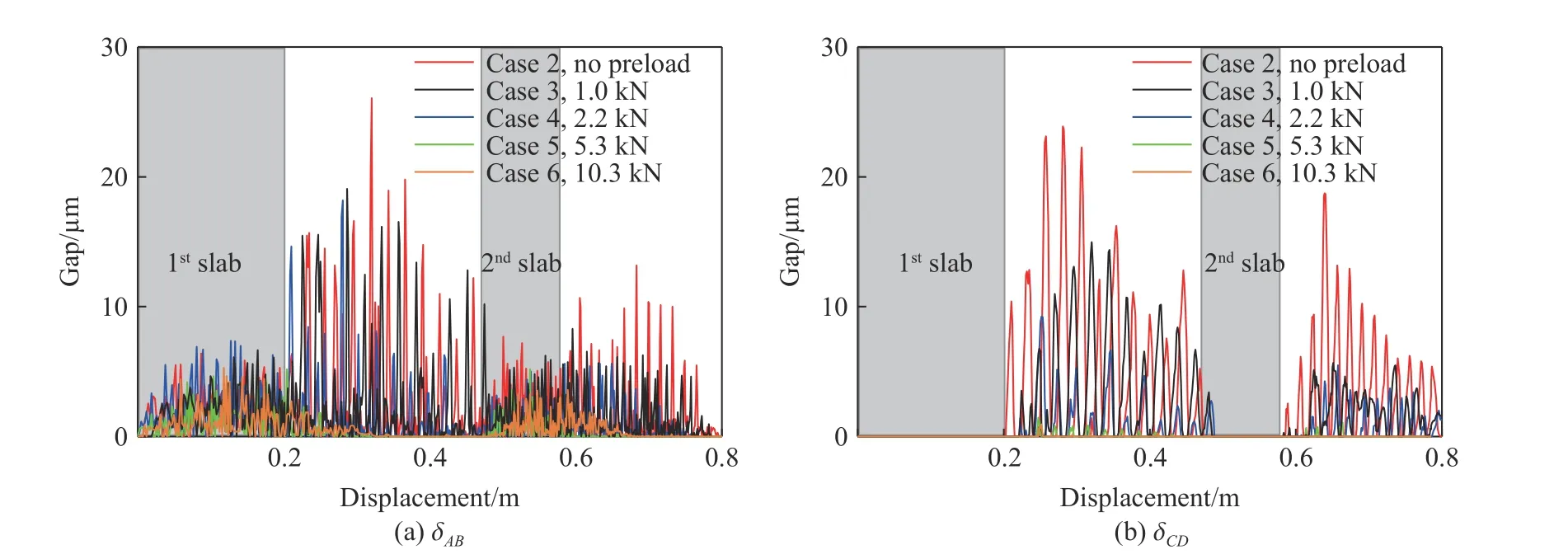
图5 不同预紧安装时装置与弹仓间隙（δAB，δCD ）的变化历程Fig. 5 Gaps of δAB and δCD versus the displacement of projectile with different preloads

综上所述，当装置与弹体为压装连接时，侵彻时二者间隙出现动态变化。抑制层间间隙的最小安装预紧力在2.2～5.3 kN 之间。层间阶段非零间隙的存在将引入间隙碰撞，后面将基于加速度信号的时频特征分析，研究间隙碰撞等对信号粘连的影响。

2 压装连接与加速度计层间信号粘连的关联性

2.1 压装连接与理想刚性连接近似的判断方法

加速度计测量的信号反映的是经多个连接结构、间断界面等传递至加速度计局部位置的加速度响应a(t)，主要包括整弹刚体过载ar(t)以及应力波传播、界面间隙碰撞等引入的附加加速度av(t)，可表示为

本研究将数值仿真获得的加速度计过载与试验中加速度计测量的加速度信号对应。

图6 展示了表4 中6 种工况下的整弹过载时域曲线。图7 展示了没有预紧压装时整弹和加速度计过载时域曲线。由图6 和图7 可知，压装连接不影响整弹的刚体运动，且加速度计过载为弹体刚体过载与一定幅值的高频振荡的叠加，符合式(1)的理论描述。

图6 6 种工况的整弹过载时域曲线Fig. 6 Time histories of deceleration of the whole projectile for 6 cases

图7 6 种工况的加速度计及整弹的过载时域曲线Fig. 7 Time histories of deceleration of the accelerometer and whole projectile for 6 cases

以着靶时刻为零时刻，将侵彻过程划分为4 个阶段。阶段Ⅰ：弹体侵彻第1 层靶板，0 ms≤t<0.52 ms。阶段Ⅱ：弹体在两层靶板之间飞行，0.52 ms≤t<1.10 ms。阶段Ⅲ：弹体侵彻第2 层靶板，1.10 ms≤t<1.65 ms。阶段Ⅳ：弹体在第2 层靶后飞行，t≥1.65 ms。

在阶段Ⅰ和阶段Ⅲ，6 种工况的加速度计过载特征无明显差别。在阶段Ⅱ和阶段Ⅳ，加速度计过载振荡的幅值在理想刚性连接时最小，无预紧压装时最大。安装预紧力可适当减小过载振荡幅值，更接近理想刚性连接。然而，时域特征的定性分析无法定量判断压装连接能否与理想刚性连接近似。

采用加窗傅里叶分析获得加速度计过载的频响特征，时间窗口与图7 的阶段划分一致。在理想刚性连接（工况1）与无预紧压装（工况2）时，各阶段加速度计过载频响分别如图8 和图9 所示。由图8 和图9 可知，在阶段Ⅰ与阶段Ⅲ，加速度响应主要集中在小于5 kHz 的低频区域，在16.8 kHz有较小的响应峰。两种连接状态的频域曲线类似。不论是理想刚性连接（工况1）还是无预紧压装（工况2），在相同的工况下，阶段Ⅱ与阶段Ⅳ的频响特征相似。工况1 的加速度计过载频响均为单峰结构，而工况2 则均为多峰结构。

弹体模态分析显示：图8 和图9 中的响应峰值频率16.8、16.2 kHz 与整弹一阶伸缩固有频率接近；图9(b)中响应峰值频率32.5 kHz 与装置一阶伸缩频率接近。弹体的典型固有频率与振型描述见表5。对于工况2，弹体在层间及靶后飞行阶段，装置与弹仓的最大间隙约25 µm，二者发生高频碰撞，这是图9(b)中出现32.5 kHz 高频响应峰的可能原因。

表5 理想刚性连接时弹体典型的固有频率及振型描述Table 5 Eigen frequency and vibration modes of projectile with ideal rigid connection

图8 在理想刚性连接（工况1）与无预紧压装（工况2）时弹靶相互作用阶段加速度计过载频域曲线Fig. 8 Frequency response of deceleration of accelerometer for ideal rigid connection (Case 1) and pressed connection without preload (Case 2) during stage Ⅰ and stage Ⅲ

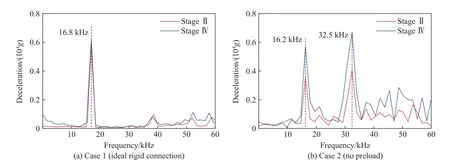
图9 理想刚性连接（工况1）与无预紧压装（工况2）时靶间及靶后飞行阶段加速度计过载的频域曲线Fig. 9 Frequency response of deceleration of accelerometer for ideal rigid connection (Case 1) and pressed connection without preload (Case 2) during stage Ⅱ and stage Ⅳ

本研究主要关注层间信号的特征。图10 展示了不同初始预紧压装时层间阶段加速度计过载的频响。由图10 可知，预紧力小于2.2 kN 时，加速度计过载呈多峰结构；预紧力大于5.3 kN 时，加速度计过载频响为单峰结构，与理想刚性连接时的特征一致。层间加速度计过载频响的单峰特征可用于判定压装连接与理想刚性连接近似是否成立。本研究中当弹靶的最小预紧力在2.2～5.3 kN 区间时，可以将压装连接近似为理想刚性连接。

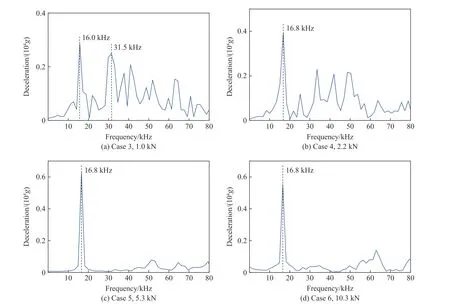
图10 层间飞行时不同安装预紧下加速度计过载频域曲线Fig. 10 Frequency response of deceleration of accelerometer with different preloads between two slabs

2.2 压装连接对加速度层间信号粘连的影响

2.2.1 着靶速度的影响

前面的研究仅关注着靶速度为597 m/s 时的情况。当撞击速度分别增至800 与1 000 m/s 时，理想刚性连接与无预紧压装连接时加速度计过载的时域响应，如图11 所示。由图11 可知：着靶速度越高，层间加速度信号粘连越显著；无预紧压装时，加速度信号的粘连现象更加明显。施加适当的预紧力可减小层间加速度过载振荡的幅值，缓和信号粘连的问题，如图12 所示。

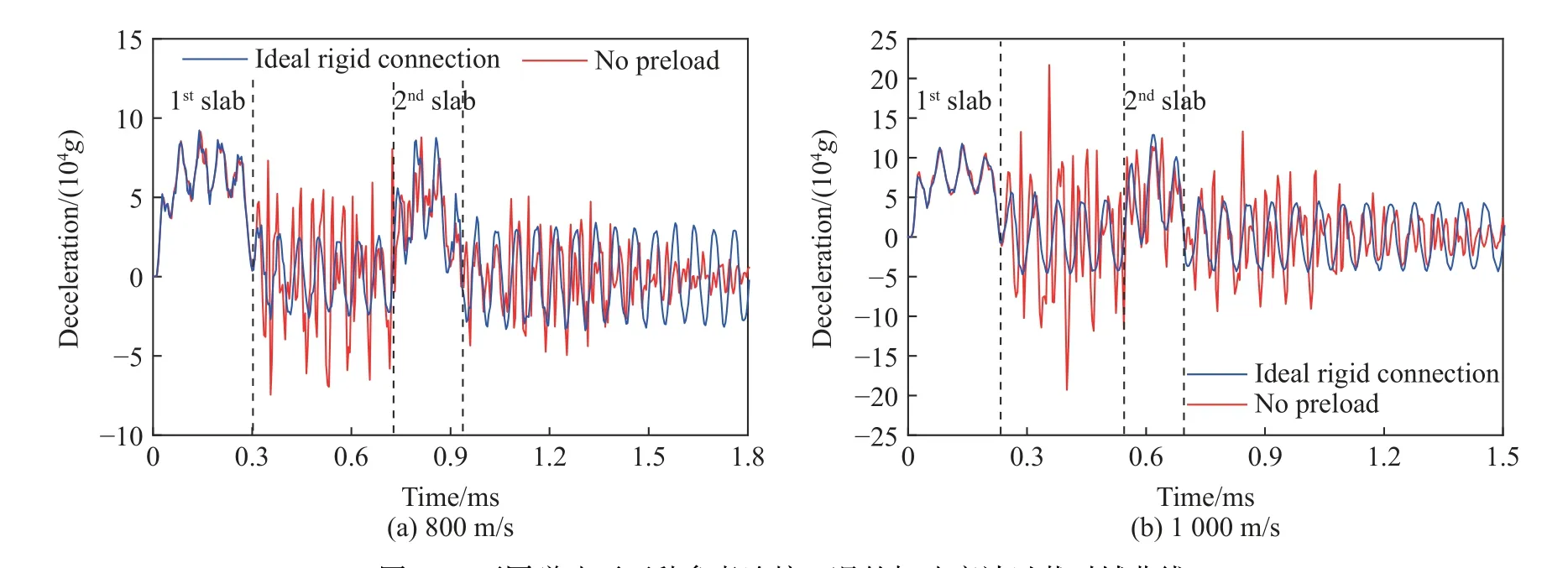
图11 不同弹速下两种参考连接工况的加速度计过载时域曲线Fig. 11 Time histories of deceleration of accelerometer for two reference cases at different impact velocities

图12 预紧压装时不同速度下加速度计过载的时域曲线Fig. 12 Time histories of deceleration of accelerometer for pressed connection with different preloads at different impact velocities

采用加窗傅里叶分析不同连接状态的层间加速度过载信号，所得结果如图13 所示。很明显，即使撞击速度不同，刚性连接时，加速度计层间过载频响均呈现单峰结构，响应峰值频率均在16.8 kHz 附近；无预紧压装时，对应的过载频响均呈现多峰结构，响应峰值频率在16.2 kHz 及更高位置处。以加速度计层间过载频响单峰结构判断：初速为597 m/s 时，压装连接与理想刚性连接近似成立的最小安装预紧力在2.2～5.3kN 之间；初速为800 m/s 时，其值在5.3～10.3kN 之间；初速为1 000 m/s 时，其值大于10.3 kN。撞击速度越高，压装连接与理想刚性连接近似成立所需的最小预紧力越大。

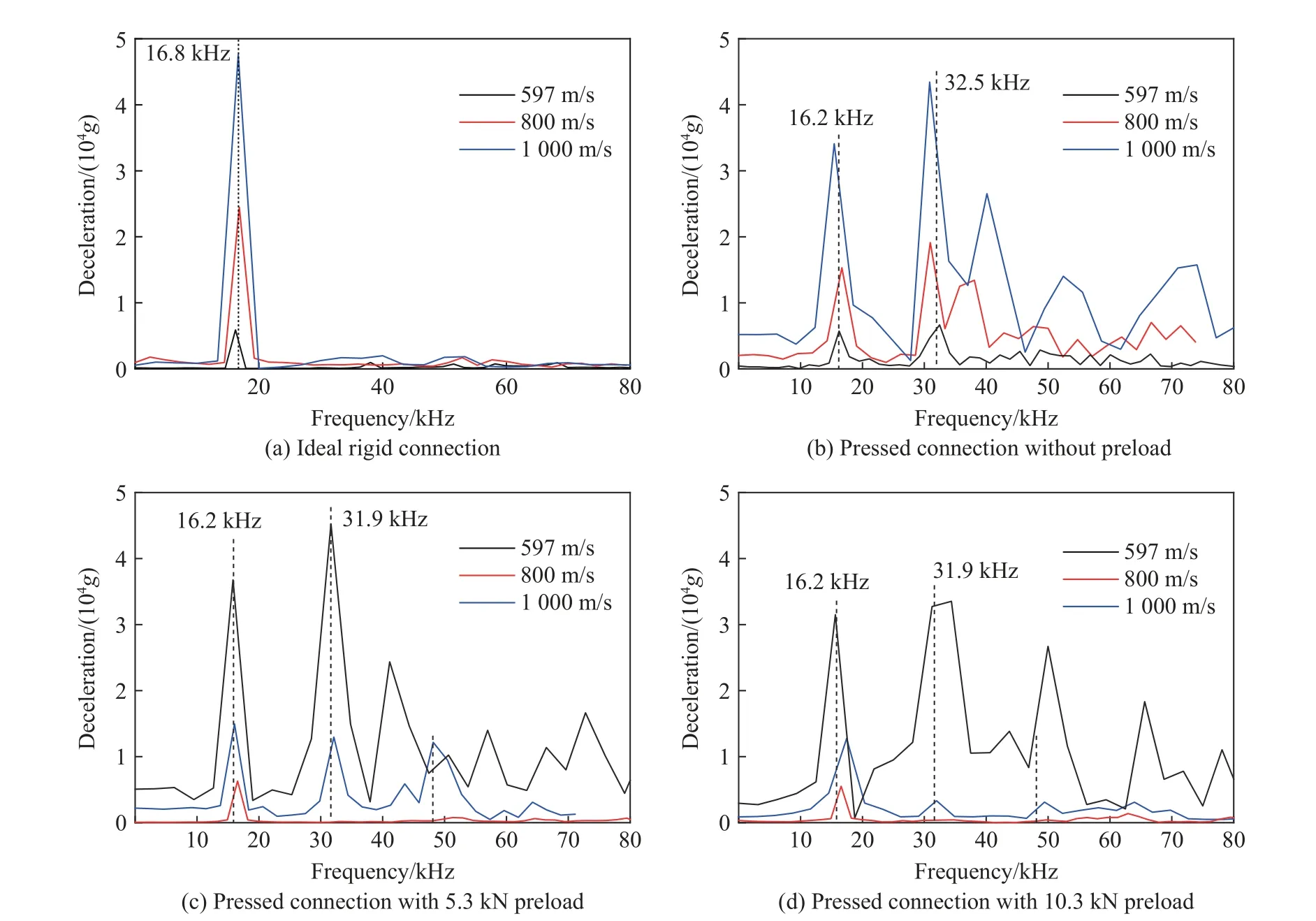
图13 不同连接状态时不同着靶速度下加速度计层间过载信号的频域响应Fig. 13 Frequency response of deceleration of accelerometer between two slabs for different connection modes at different impact velocities

不同撞击速度时弹体中典型位置的等效应力随时间变化历程如图14 所示。由图14 可知，撞击速度越高，弹体中相同位置的等效应力最大值越大。尽管在层间及靶后飞行时弹体无外载作用，但仍有高幅值的应力波留存在弹体中。由简单的弹性变形理论可知，应力越大，对应的变形量越大，装置与弹体间更易形成间隙。这就是更高撞击速度时需要更大安装预紧才能使压装连接与理想刚性连接近似的原因。

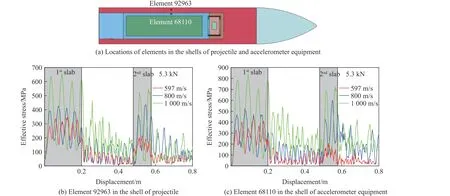
图14 以不同着靶速度穿越双层靶时弹体与装置典型位置的应力变化历程Fig. 14 Time histories of effctive stress for the elements in projectile and in accelerometer equipment during perforating two slabs at different initial impact velocities

2.2.2 靶标层数的影响

实际多层靶可能在3 层以上[3-5,18]，加速度层间信号粘连可能更显著。为此，设计了5 层多层间隔混凝土靶标（单层厚50 mm），靶间距150 mm，弹体以着靶速度600 m/s 正侵彻靶标，其余条件与文献[13]保持一致。分析了装置与弹体在理想刚性连接、无预紧压装以及5.3 与10.3 kN 预紧压装4 种连接状态下加速度计与整弹的过载时域响应，结果如图15 所示。由图15 可知，即使装置与弹体为理想刚性连接，第2 层靶板后层间信号粘连加剧。无预紧压装连接时，层间信号粘连更显著。施加适当的安装预紧后，加速度计的层间信号的时域响应与理想刚性连接时信号的时域响应类似。

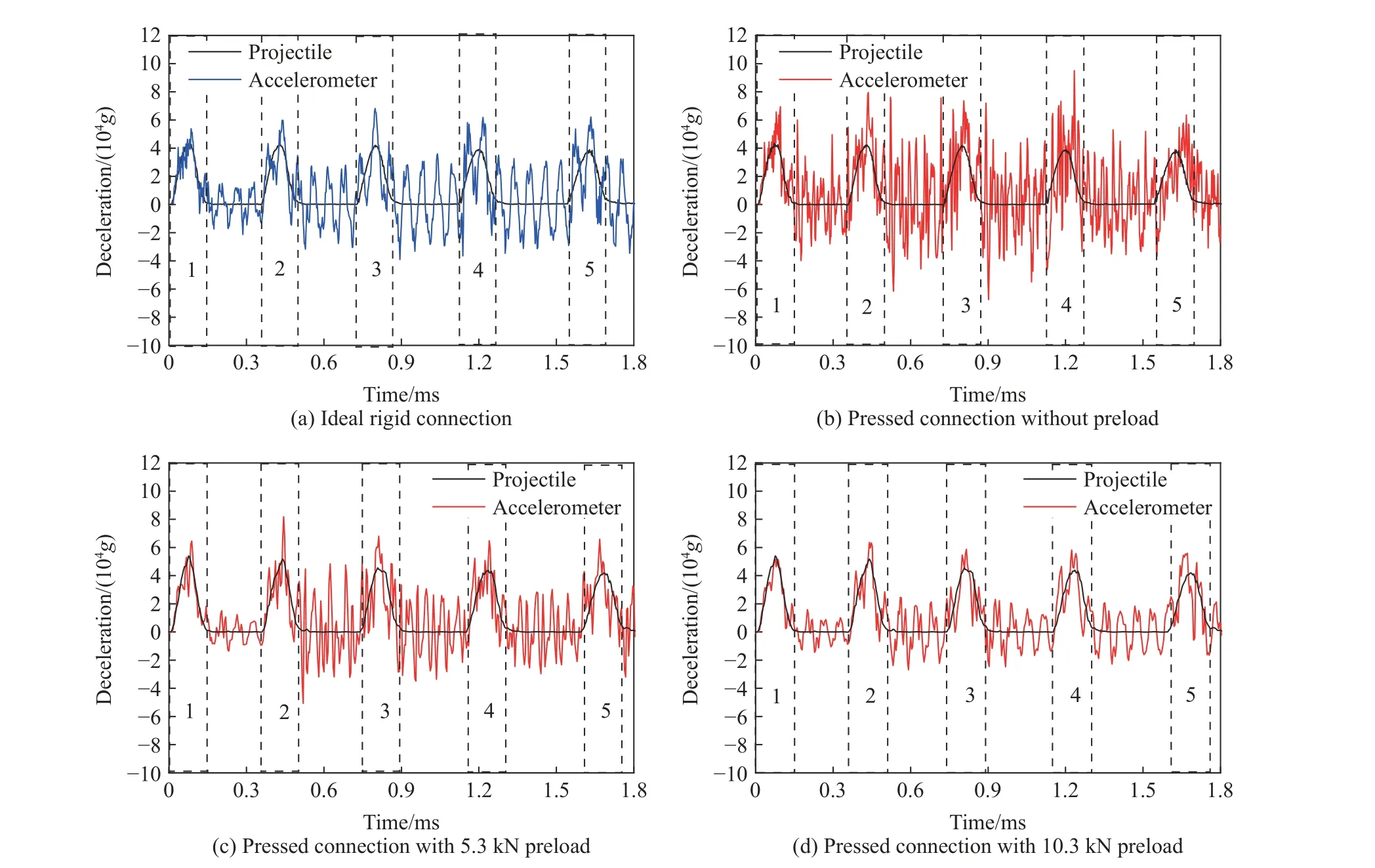
图15 初速为600 m/s 的弹体侵彻5 层靶时加速度计和弹体刚体过载的时域曲线Fig. 15 Time histories of deceleration for accelerometer and projectile during perforating 5-layer target at an initial impact velocity of 600 m/s

图16 展示了与图15 对应的层间加速度计过载的频域响应。由图16 可知，理想刚性连接时，各个层间的加速度计过载频响均为单峰结构。无预紧压装时，各层间加速度计过载频响为多峰结构。当初始安装预紧力为5.3 kN 时，第1 层与第2 层（1-2 层）之间的加速度计过载频响为单峰结构；在后续的2-3 层、3-4 层、4-5 层及第5 层靶板后，加速度计过载频响均为多峰结构。当安装预紧力增至10.3 kN时，各层间加速度计过载频响均为单峰结构。这说明弹体以初速600 m/s 打击多层靶时，可将压装连接近似为理想刚性连接的最小安装预紧力在5.3～10.3 kN 之间。因此，在类似的弹体初速下，打击多层靶时的最小安装预紧力较打击双层靶时有所增加。

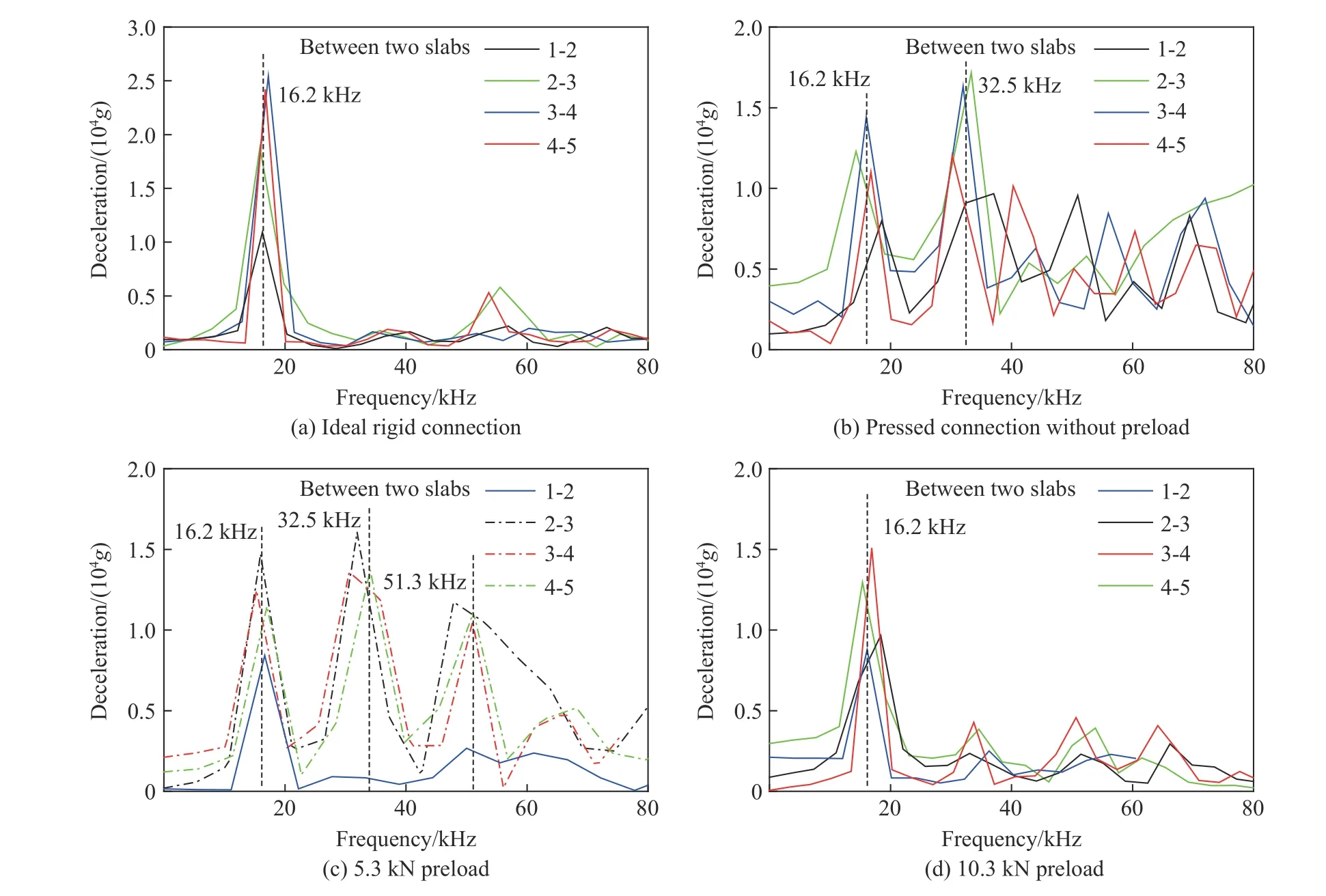
图16 弹体初速为600 m/s 时4 种连接状态下层间加速度计过载频域响应Fig. 16 Frequency responses of the deceleration of accelerometer with 4 connection modes as a function of frequency during perforating two neighboring slabs at an initial impact velocity of 600 m/s

图17 展示了穿过5 层靶时弹体和装置的典型位置的应力时程曲线。由图17 可知，在1-2 层间，弹体外壳与装置内留存的应力波最大值小于100 MPa；在后续的2-3、3-4、4-5 层间及5 层后，应力波最大值可达200 MPa，与图14 中着速800 m/s 时层间飞行留存的应力波最大值相当。这说明打击5 层靶时，压装连接与理想刚性连接近似所需的最小预紧力应与弹体初速800 m/s 打击双层靶的预紧力相当。二者的最小预紧力均在5.3～10.3 kN 之间，与分析结论一致。

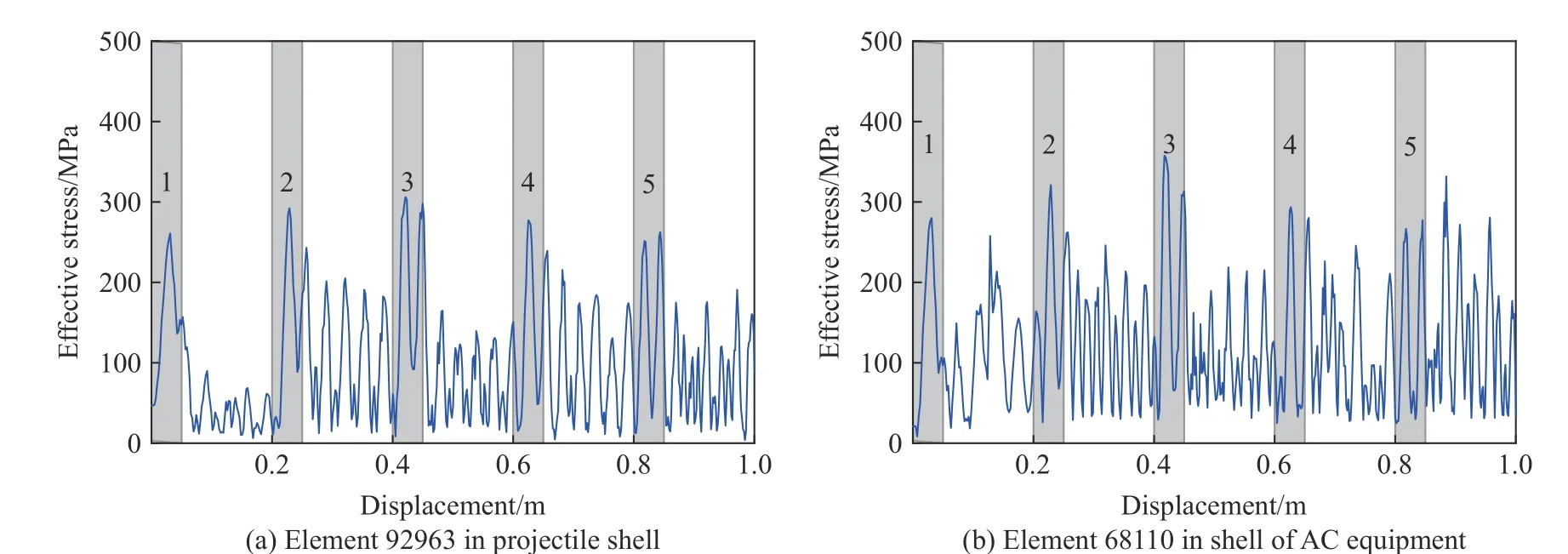
图17 弹体以600 m/s 的初速穿过5 层靶时弹体与装置典型位置的应力变化历程Fig. 17 Time histories of elements for projectile and accelerometer equipment during perforating five slabs at an initial impact velocity of 600 m/s

综上所述，装置与弹仓的间隙碰撞会加剧加速度层间信号粘连。存在可使压装连接与理想刚性连接近似的最小的安装预紧力，当预紧力超过最小安装预紧力时，间隙碰撞可以被抑制，此时，加速度计层间过载频响为单峰结构，响应峰值频率在弹体一阶伸缩固有频率附近。最小安装预紧力随撞击速度、穿靶层数的增加而增大，其机理在于弹体中留存的应力波最大值随撞击速度、穿靶层数增加而增大。

3 结 论

采用数值仿真手段，并辅以理论分析，对装置与弹体在理想刚性连接和不同预紧压装连接下弹体侵彻多层靶的动力学响应进行了分析，获得了如下结论。

(1)压装连接时，在侵彻的高过载环境下，加速度测量装置与弹体间形成动态间隙，产生高频间隙碰撞。存在最小安装预紧力，可在层间阶段抑制二者的间隙，如本研究中弹体以着速597 m/s 撞击双层混凝土靶时，最小安装预紧力在2.2～5.3 kN 之间。

(2)可利用层间及靶后飞行阶段加速度计的过载频响特征来判断压装连接能否与理想刚性连接近似。频响为单峰结构，且响应峰值频率在弹体一阶伸缩固有频率附近时，压装连接可近似为理想刚性连接；频响为多峰结构，则压装连接不能近似为理想刚性连接。存在最小安装预紧力，可使压装连接与理想刚性连接近似，缓和压装连接引入的附加层间加速度信号粘连的问题。

(3)本研究的弹靶撞击速度从597 m/s 增至800 和1 000 m/s 时，压装连接与理想刚性连接近似的最小预紧力从2.2～5.3 kN 区间分别增加至5.3～10.3 kN 以及大于10.3 kN 区间。以600 m/s 撞击5 层靶所需最小预紧力在5.3～10.3 kN 之间。这说明撞击速度越高，或靶标层数越多，压装连接与理想刚性连接近似的最小安装预紧力越大。这是因为层间阶段弹体中应力波最大值随撞击速度、穿靶层数增加而增大。

本研究结果可为引信中硬件滤波截至频率的选择提供参考，对压装连接的预紧力施加也有一定的指导作用。未来将关注加速度测量装置形态、弹体侵彻姿态等对压装连接动态响应的影响，全面分析各参数对压装连接与理想刚性连接近似的影响，为消除压装连接引入的信号粘连提供支撑。