基于质心频率的薄层识别研究及应用

杨登锋，吴 静，白海军

(中海石油(中国)有限公司深圳分公司 研究院，广东 深圳 518054)

1 引 言

随着勘探开发的不断深入，岩性圈闭逐渐成为勘探开发的重点领域。岩性圈闭的储层具有隐蔽性强、厚度薄的特点。因此，薄层砂体厚度的准确识别及其平面展布的有效刻画是岩性圈闭勘探的关键[1-3]。

对于薄层识别，众多专家学者已经做了大量研究。Widess首次通过楔状体模型研究薄层地震反射特征，将厚度小于子波1/8主波长的地层定义为薄层[4]。Neidell等在研究振幅强度与薄层厚度的关系时，引入了调谐厚度概念并将其作为划分薄层的依据,即小于1/4主波长的地层为薄层[5]。地震反射振幅在薄层厚度等于1/4主波长时达到最大，随着薄层逐渐变薄，地震反射振幅也逐渐减小。薄层地震反射的这一特性为利用地震振幅属性识别薄层奠定了理论基础[6-8]。例如，凌云研究小组根据地震反射振幅的调谐作用探测地层厚度小于1/4波长的薄层[9]。另外，很多研究同样发现薄层厚度的变化会影响地震波的频谱特征，即当地层厚度小于1/4波长时，薄层厚度逐渐变薄，反射波峰值频率逐渐变大[10-13]。根据这一特征，峰值频率同样被用来识别薄层[14-16]。

由于实际地震资料中通常存在噪声干扰，会影响均方根振幅和峰值频率两种属性识别薄层的稳定性。另外，受地震采集、处理等因素影响，导致反射波的振幅能量不均衡，降低了振幅属性识别薄层的可靠性。为了提高薄层识别的稳定性和可靠性，提出利用质心频率来识别薄层，并通过模型测试和实际资料应用以验证质心频率识别薄层的有效性。

2 基本理论

当假定薄层顶底反射系数分别为r1和r2，经过傅里叶变换薄层反射系数序列频谱可以表示为[11]

R(f)=r1e-i2πft1+r2e-i2πft2

(1)

其中，f为频率，单位Hz；t1和t2分别为薄层顶底界面的双程旅行时,单位s。经整理得到反射系数序列振幅谱为[15]

(2)

其中，Δt=t2-t1为子波在该薄层中传播的双程旅行时，单位s。

主频为fm的雷克子波振幅谱可表示为[17]

(3)

当地震子波在地层中传播时，地层可以看成一个滤波器，地震子波为该滤波器的输入。地震子波经过薄层其地震响应振幅谱A(f)可以表示为地震子波振幅谱与薄层反射系数振幅谱的乘积，如下所示

A(f)=W(f)•AR(f)

(4)

将上式对频率f求导并令其为零，得到峰值频率fp有如下关系式[14]

(5)

其中,R=r1/r2。对上式进行泰勒展开近似，并令R=-1，经整理得到峰值频率fp与薄层厚度Δt之间关系式为[15]

(6)

由上式可以看出，薄层厚度Δt越小，峰值频率fp越大，因此可以用峰值频率fp刻画薄层厚度。由于峰值频率是振幅谱最大值对应的频率，其稳定性很容易受噪声影响。为了提高峰值频率属性识别薄层的稳定性，这里选用质心频率替代峰值频率，质心频率fc表达式为[18]

(7)

质心频率求取过程中涉及到能量谱积分求和，受噪声影响小、更稳定[19-21]。

3 理论模型研究

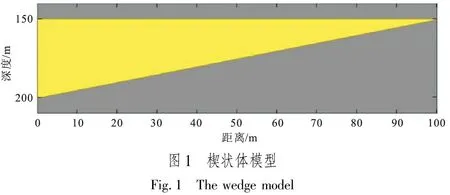
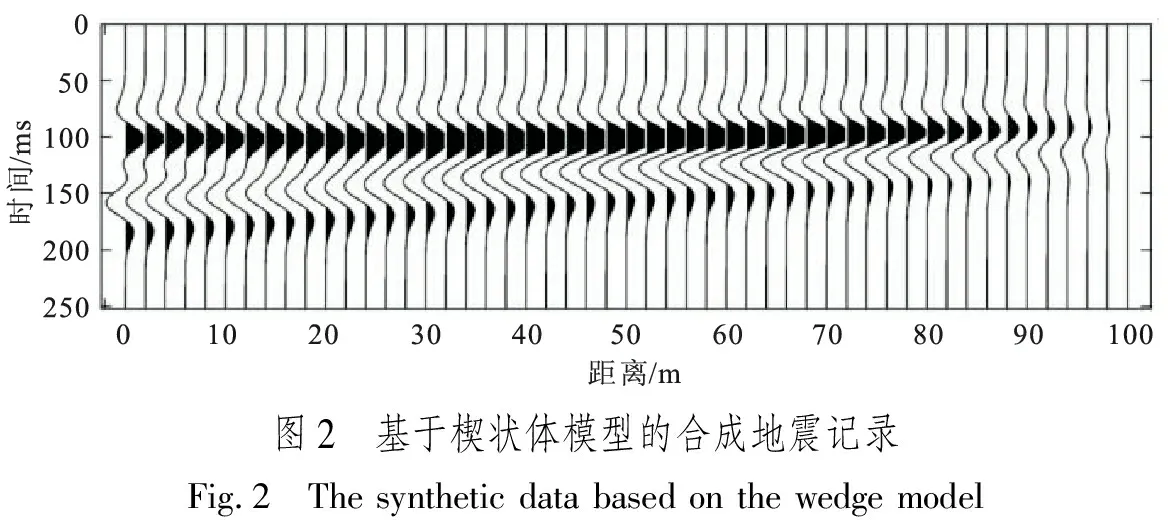
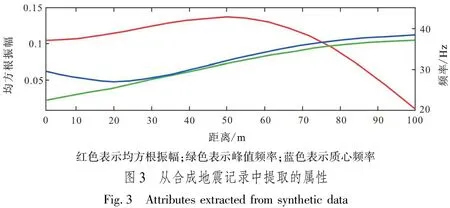
首先设计一个楔状体模型，研究质心频率与砂体厚度之间的关系，分析其识别薄层的可行性。图1为该楔状体模型，其中黄色代表砂岩，速度为3 500 m/s，密度为2.5 g/cm3，最大厚度为50 m；灰色代表泥岩，速度为3 000 m/s，密度为2.25 g/cm3。图2是选用主频30 Hz的雷克子波与该楔状体模型进行褶积运算得到的合成地震记录。基于该合成地震记录提取楔状体顶面地震反射均方根振幅、峰值频率和质心频率三种属性，如图3所示。从图3中可见，均方根振幅在砂体厚度约为25 m(水平距离50 m)处达到最大，该厚度对应于1/4波长；随着砂体厚度减薄，振幅逐渐减弱。当砂体厚度小于1/4波长时，图3中峰值频率和质心频率都随着砂体的变薄而逐渐增大。砂体越薄，质心频率越大，从而证实利用质心频率定性识别薄层砂体厚度是可行的。

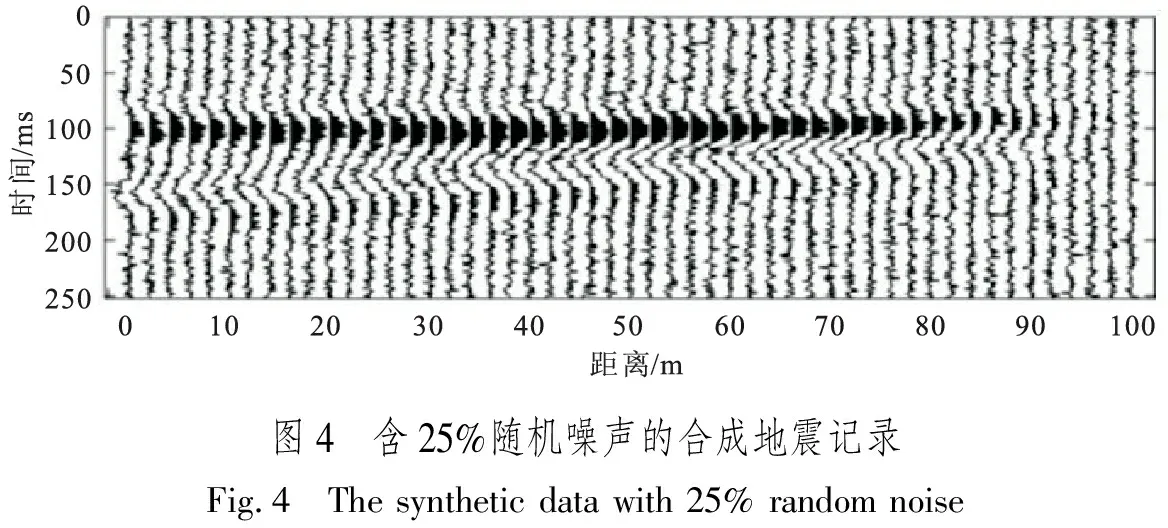
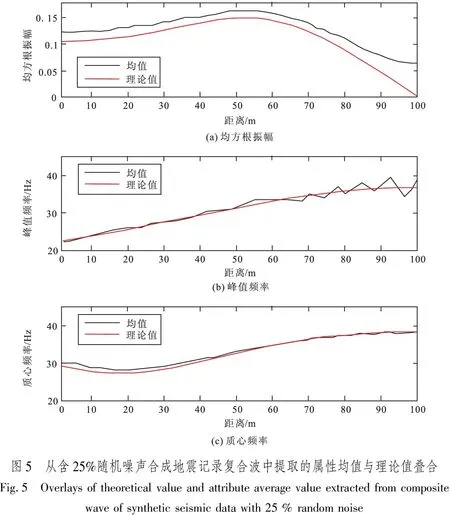
实际地震资料通常存在一定的噪声干扰，影响地震属性识别薄层的稳定性。这里，在图2合成地震记录中加入随机噪声，对比分析均方根振幅、峰值频率和质心频率识别薄层的稳定性。图4为含25%(最大振幅值的25%)的随机噪声的合成地震记录。在含噪声的合成地震记录中分别提取以上三种属性，进行200次独立试验，每次独立试验都重新生成25%的随机噪声，计算它们的均值和相对标准差(标准差除以理论值)。图5为计算的各属性均值和理论值叠合图，其中红色线条为理论值、黑色线条为计算均值。从图5中可以看出，均方根振幅均值与理论值叠合程度稍差，砂体越薄均值越偏离理论值；峰值频率的均值与理论值在薄层段叠合一致性较差且波动明显；质心频率的均值与其对应的理论值叠合的比较好，当砂体变薄时，均值曲线呈现细微波动。另外，图6展示了三种属性的相对标准差。从图中可见，当砂体厚度小于1/4波长时，随着砂体厚度变薄，相对标准差都逐渐变大，三种属性识别薄层的稳定性都有所降低。但是，当砂体厚度小于1/4波长时，在同一水平距离处，质心频率相对标准差要明显小于均方根振幅和峰值频率相对标准差。通过含噪声数据测试证实：相较于均方根振幅和峰值频率，质心频率均值与理论值匹配的更好、波动更小，并且其相对标准差最小；即质心频率识别薄层的稳定性表现得更好，抗噪能力更强。

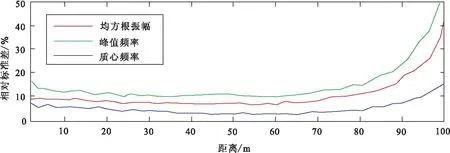
图6 从含25%随机噪声合成地震记录复合波中提取三种属性相对标准差

此外，由于受地震采集、处理等客观因素影响，导致地震反射波振幅不保幅，不同地震道中地震波的能量不均衡。这里通过合成能量不均衡的地震记录，对比分析上述三种属性识别薄层的可靠性。基于图1楔状体模型合成能量不均衡地震记录，如图7所示。从中提取均方根振幅、峰值频率和质心频率，如图8所示。从图8(a)中可见，当地震反射波能量不均衡时，均方根振幅曲线与理论值曲线存在明显差异；而图8(b)中的峰值频率和图8(c)中的质心频率曲线与理论值曲线完全重合，不受地震波振幅强度的影响。图8表明，在能量不均衡的地震记录中，质心频率依然能够可靠地识别薄层。

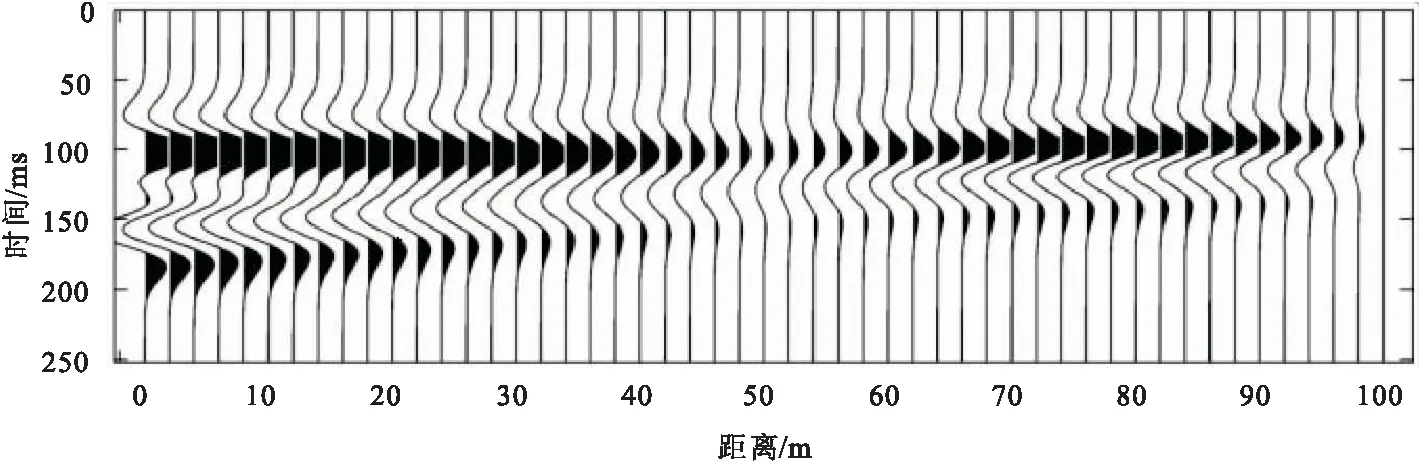
图7 能量不均衡的合成地震记录

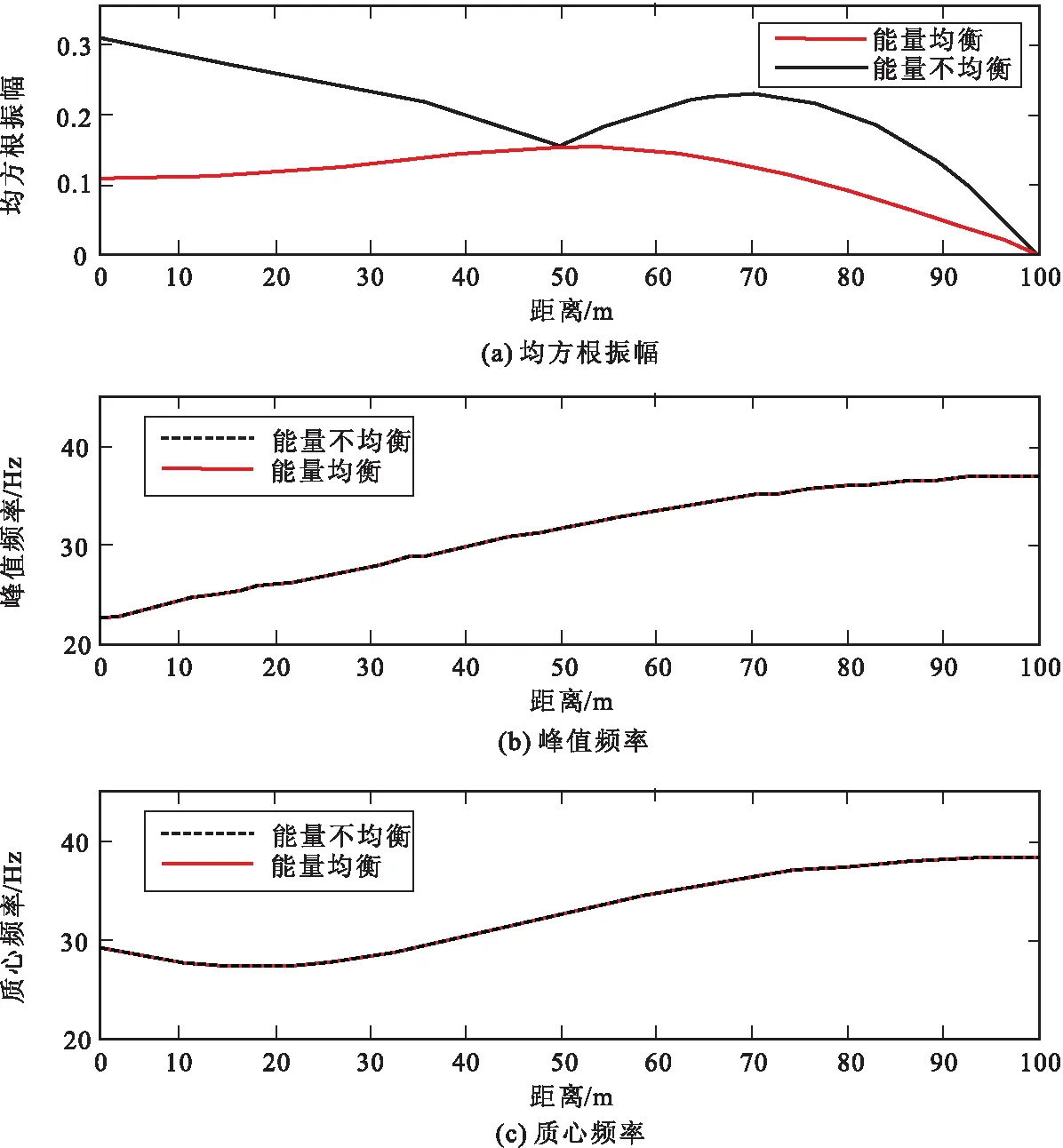
图8 基于图7合成地震记录提取的属性

4 应用实例和效果

珠江口盆地A凹陷南部珠江组以三角洲前缘近端或远端沉积为主，沉积过程中由于受波浪搬运和改造，在三角洲前缘外侧常形成平行于岸线的条带状陆架砂脊和砂席。这些陆架砂脊和砂席沉积厚度较薄，常规地震剖面上难以直接识别。

图9是沿着主要目的层地震反射分别提取的均方根振幅和质心频率属性。从图9中可见，该目的层在研究区内的分带特点比较明显。在研究地区的西部，均方根振幅属性图上振幅能量较强，与之相对应的区域质心频率表现为低频特征。该地区靠近古珠江物源方向，砂体沉积厚度相对较厚，与模型测试中相对厚砂体表现为强振幅、低频率的特征相匹配。在研究地区的东部，均方根振幅属性图上呈现北东向分布的振幅能量强弱分明的条带；在质心频率属性图上同样的位置也表现为明显的条带状，强振幅条带对应于低频条带，弱振幅对应于中高频条带。图上强振幅、低频率区发育相对较厚的陆架砂脊，储层物性相对较好。在该区域钻探3口探井H1、H2和H3井，三口井在该目的层条带区都钻遇薄层砂体。砂体厚度H1井为20m、H2井为16m、H3井为7.2m。实钻砂体厚度与质心频率属性对应关系比较好，相对厚砂体对应低频率，薄砂体对应高频率。实际应用证实了质心频率属性定性识别薄层砂体厚度是可行、有效的。

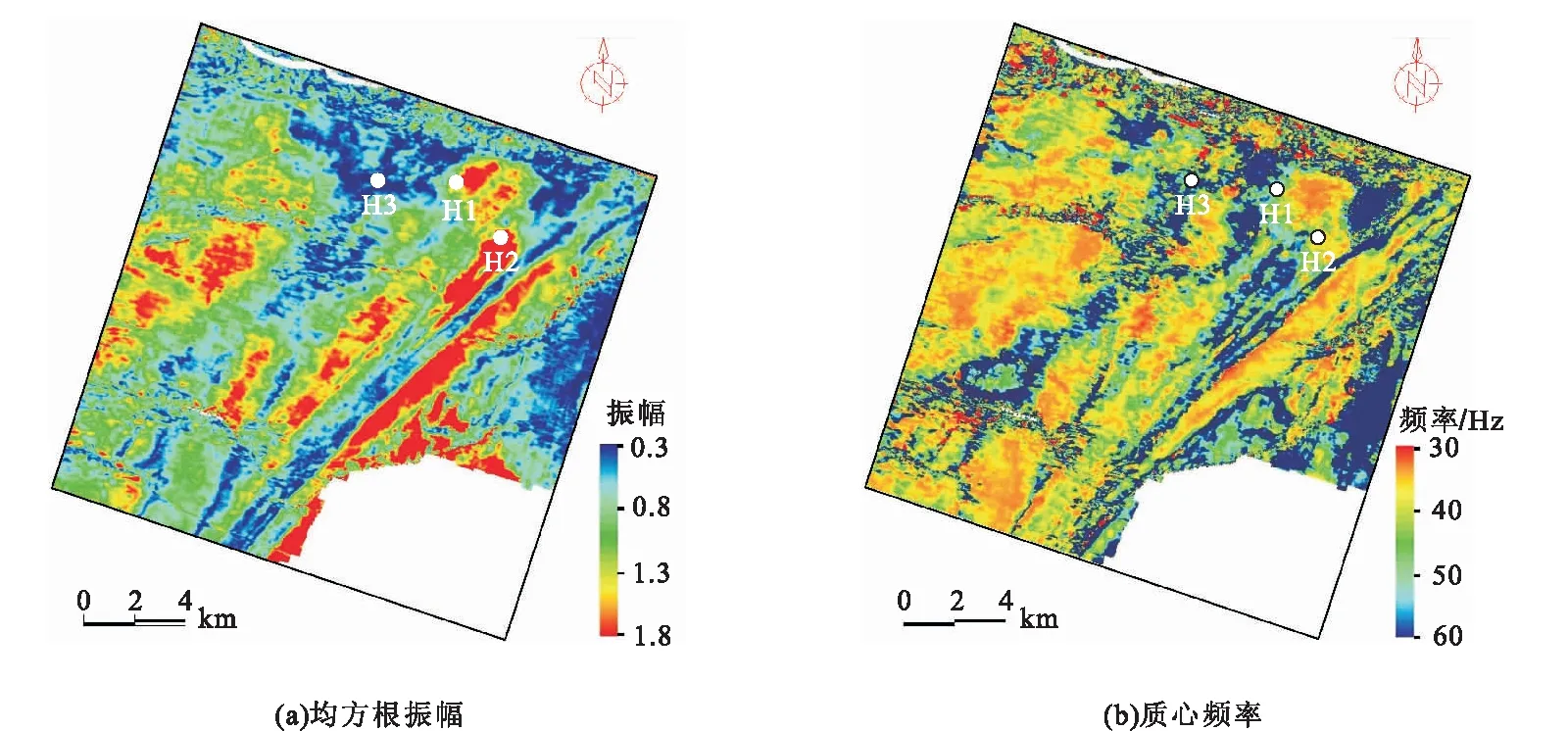
图9 沿目的层提取的属性平面分布

另外，A凹陷面积大、范围广，拥有多套不同年度采集处理的三维地震资料。部分地质目标就处在这些三维地震资料的拼接处，不同年度采集处理的地震资料振幅能量存在差异，影响振幅属性识别薄层厚度的可靠性。某薄层岩性体范围内包含两套地震资料，拼接线两边地震反射振幅能量不均衡，如图10所示。在目标区目的层提取均方根振幅和质心频率属性，分别如图11(a)和图11(b)所示。图11(a)中的均方根属性上存在明显的拼接痕迹，拼接线两边均方根振幅差异明显，不能可靠地反映目的层薄层砂体的平面展布特征。然而，图11(b)中的质心频率属性不受资料拼接的影响，在拼接线两边没有明显的突变，可以有效反映薄层砂体的厚度的平面变化和沉积特征。通过该实际资料的应用，证实了在能量不均衡的地震资料中质心频率可以可靠识别薄层。

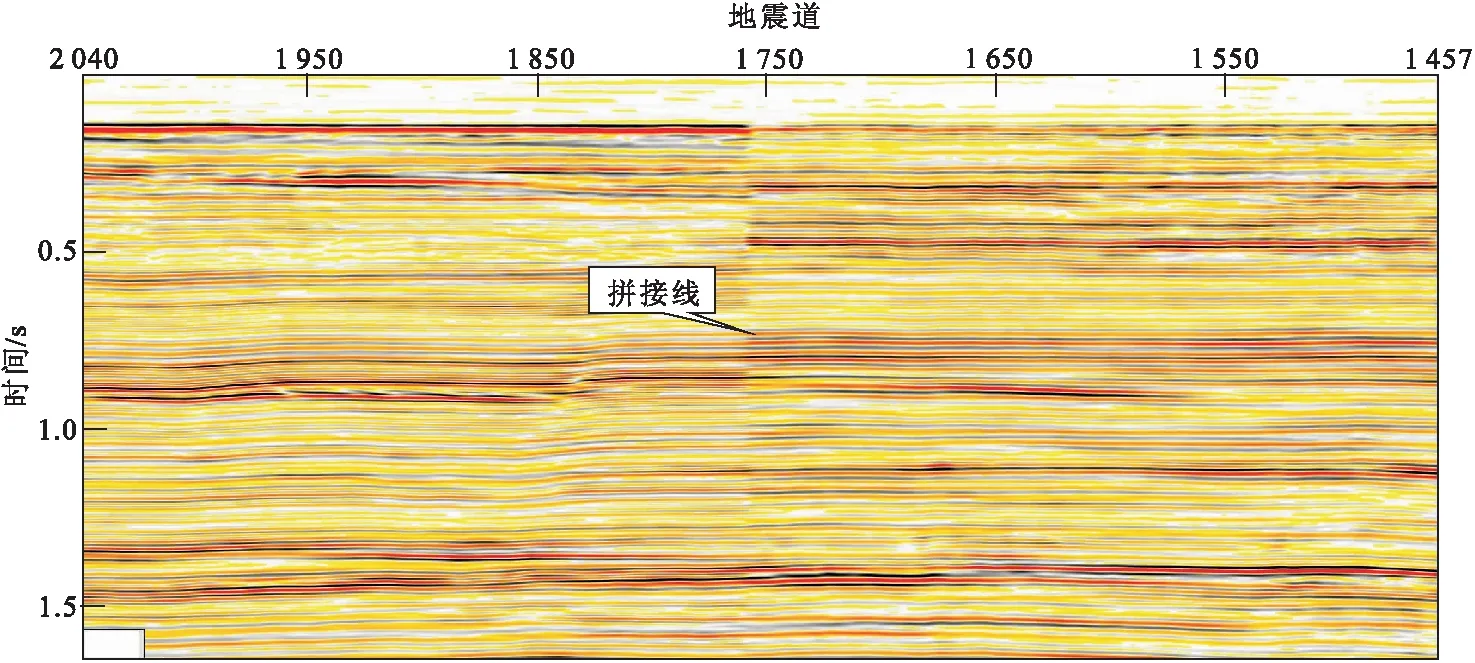
图10 目标区过拼接线的地震剖面

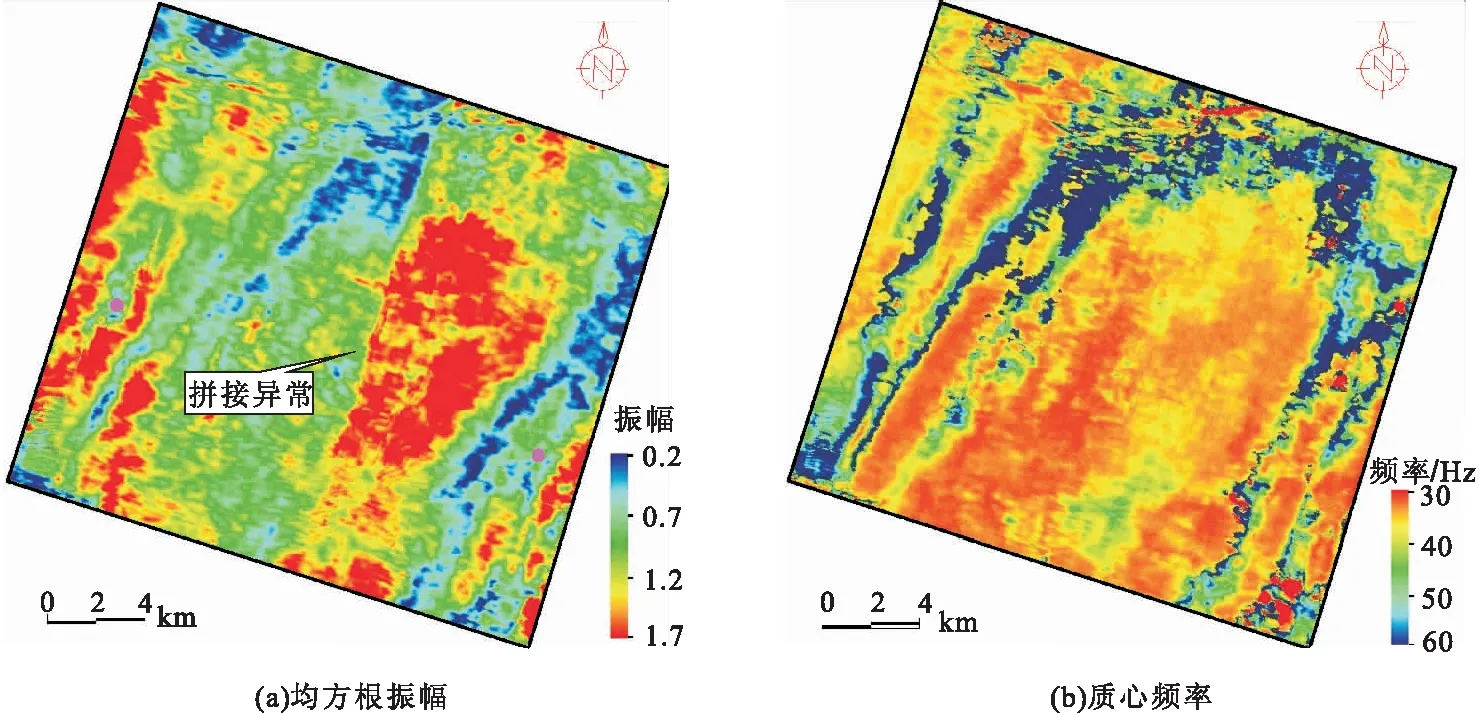
图11 沿目的层提取的属性平面分布

5 结 论

1)薄层厚度与质心频率之间表现如下关系：当砂体厚度小于1/4波长时，砂体越薄，质心频率越大。利用质心频率定性识别薄层砂体厚度是可行的。

2)在随机噪声干扰的地震记录中识别薄层，相对于均方根振幅和峰值频率，质心频率的稳定性表现得更好，具有更强的抗噪能力。

3)相对于均方根振幅，在能量不均衡的地震记录中，质心频率识别薄层更可靠。