重磁异常独立成分分析的多道信号构建方法

杨明豫，杜劲松,3，王 震，袁常青，胡正旺

(1.中国地质大学 地球物理与空间信息学院，湖北 武汉 430074；2.中国地质大学 地球内部多尺度成像湖北省重点实验室，湖北 武汉 430074；3.中国地质大学 地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

1 引 言

重磁勘探通过测量与校正处理获得的重磁异常观测数据，是地下不同规模与不同埋深的地质异常体在测点上产生的重磁异常信号的线性叠加，而往往勘探目标是明确的，因此异常分离是重磁资料处理的一个基本的也是关键的环节之一。该问题实际上可以将其视为盲源信号分离问题(Blind Source Separation, BSS)，即从若干观测到的混合信号(观测重磁异常数据)中恢复出无法直接观测的各个原始信号(地下不同规模与不同埋深的地质异常体在测点上产生的重磁异常信号)的过程，而独立成分分析(Independent Component Analysis, ICA)是盲源信号分离的一种经典方法[1]。

ICA是基于信号统计独立性最大的混叠信号分析方法，自20世纪90年代由Hyvarinen[2，3]、Cardoso[4]、Comon[5]、Jutten[6]推出快速计算方法以来，就被广泛地应用于图像处理、语音识别、生物医学、雷达探测等诸多领域[7]，在地震勘探、大地电磁与GNSS信号处理与分析等方面也取得了比较显著的应用效果[8-11]。在位场领域，由于ICA为多道信号分析方法，因此主要用于重磁时空变化信号分析方面[12-15]。对于重磁异常数据，已有一些学者开展了相关的研究工作，例如：张念[16]使用了多种盲源信号分离方法(包括ICA方法)，对比分析了其在静态重磁数据处理中的应用效果，并利用模型试验验证了重磁异常信号的非高斯性，从而使其满足ICA算法的基础假设，之后利用相邻剖面法构建输入数据，对重磁理论与实际信号进行ICA分解，证明了方法的有效性；王成彬等[17]利用ICA方法对EMD分解得到的固有模态函数进行ICA分解，有效地对东天山的航磁数据进行了分离；马龙等[18]运用基于负熵最大的FastICA(固定点算法)，利用相邻剖面法来构建ICA方法所需的多道数据输入，并采用幂次方迭代的ICA算法进行了重力异常仿真实验，验证了方法在重力异常的分离和弱异常提取中的有效性，最后将其应用于实际磁测资料处理，有效地识别了不同异常体产生的磁力异常信号。上述研究表明，ICA在重磁异常去噪、异常分离与弱信号提取等方面具有较好的应用前景。但是，为了构建多通道数据，以往研究一般均是采用相邻剖面法，而张念[16]的研究表明，对于2D重磁异常，基于相邻剖面法的ICA分解具有较好的应用效果，但是对于3D情况，ICA分解效果受剖面位置影响。因此，亟须寻找一种合适的多道信号构建方法，使其在满足ICA方法对输入信号的要求的同时，具有良好的重磁异常信号分解效果，从而使ICA方法基于统计独立性的算法优势得到充分的发挥。

本文针对重磁异常ICA分析的多通道信号构建问题，提出两种多通道信号构建方法，即相空间重构法和空间延拓法，进而基于仿真数据对三种基于多通道信号构建方法的应用效果进行了对比分析，最后将基于空间延拓的ICA方法应用于实测重磁异常数据，结合其他异常分离方法计算结果以及地质资料，对本文所提方法的计算结果进行了综合分析与评价。

2 独立成分分析方法

2.1 基本原理

ICA方法是一种解决盲源信号分离问题的信号处理方法。盲源信号分离问题，即观测信号是由未知的原始信号通过未知的混合方法进行叠加得到的，进而采用可行的方法对观测信号进行分解得到原始信号的问题。如果假设观测信号是原始信号通过线性混合得到的，那么可用公式(1)表示原始信号进行混合得到观测信号的过程：

x=As

(1)

式(1)中，观测信号向量x∈Rm×n;混合矩阵A∈Rm×m;原始信号向量s∈Rm×n;m为观测信号个数;n为信号向量的长度。

由于式(1)中的已知量仅有观测信号向量x，原始信号向量s以及混合矩阵A均未知，则可知式(1)的解不唯一。为了求解式(1)，得到需要的原始信号s，需要进行如下假设：

1)原始信号向量s均值为零，且为实随机变量并统计独立；

2)原始信号向量s具有非高斯分布，且最多允许原始信号中的一个分量具有高斯分布，因为多个服从高斯分布的信号进行线性混合后得到的新信号依旧符合高斯分布，所以其不可分；

3)观测信号向量x的个数与原始信号向量s的个数相等，即混合矩阵A为方阵。

ICA方法作为一种解决盲源信号分离的方法，其目的就是为了计算得到一个解混矩阵W：

y=WTx=WTAs

(2)

式(2)中，上标T表示矩阵的转置。

通过ICA方法计算得到解混矩阵W，便可以计算出原始信号的估计y。通过式(2)也可以看出，当解混矩阵WT=A-1时，计算得到的原始信号s的估计y即为原始信号s。为了能够快速计算出解混矩阵，且使分解结果之间尽量相互独立，具有多种信号非高斯性度量参数可以作为信号间相互独立的强约束条件，包括峭度、负熵、最大似然估计等。

2.2 基于负熵的FastICA算法

FastICA算法是使用负熵作为随机变量的非高斯性的度量得到的ICA算法。熵是信息论中的基本概念，表示随机变量包含的信息量，变量越随机、越不可预测、其熵越大，对于随机变量Y而言，其熵H的定义如下：

(3)

式(3)中，ai表示随机变量Y的可能取值。此定义可以推广到具有连续值的随机变量，此时其被称为“微分熵”或“差分熵”，定义概率密度为f(y)的随机变量y的微分熵H如下：

(4)

根据相关的信息理论，在所有方差相等的随机变量中，高斯分布的随机变量具有最大的微分熵。于是根据微分熵便可以构造出一种随机变量的非高斯性度量，为了获得高斯变量为零,并且总是非负的非高斯性度量，定义随机变量y的负熵J如下：

J(y)=H(yGauss)-H(y)

(5)

式(5)中，yGauss是与y具有相同方差的高斯随机变量。由上式易知，当y具有高斯分布时，J(y)=0。随机变量y的非高斯性越强，其微分熵越小，值越大。但是，利用式(5)计算负熵非常复杂，且需要估计随机变量y的概率密度函数。为了简化计算，对负熵进行如下近似：

J(y)∝{E[G(y)]-E[G(yGauss)]}

(6)

上式中常用的函数G(y)为：

(7)

其中，1≤a1≤2。

在使用FastICA算法之前，通常需要对数据进行预处理，包括中心化与白化。中心化即保证观测信号向量的均值为零，从而保证观测信号向量满足ICA算法的假设；白化的目的是对观测信号矩阵X进行线性变换，使其协方差矩阵为单位矩阵，进而使得白化后的观测信号向量之间不相关且方差一致。观测信号矩阵X的白化过程可用下式表示：

(8)

ICA算法的目标是求解使WTx的非高斯性最大的解混矩阵W，在使用负熵作为非高斯性度量的情况下，通过式(6)简化负熵的计算复杂度后，即求解使E[G″(WTx)]达到最大值的解混矩阵W。根据Kuhn-Tucker条件，在解混矩阵W满足正交矩阵的条件下，通过系列推导可得FastICA算法迭代计算解混矩阵W的迭代公式如下[1,3,18]：

W+=E[xG′(WTx)]-E[G″(WTx)]W

(9)

迭代终止的条件可以设置为：当两次迭代计算的解混矩阵W的某一行向量的L1范数之差小于某一阈值，或迭代次数达到最大值时终止迭代。同时在迭代过程中对解混矩阵W进行正交化，从而保证求解的结果满足约束条件[1,3,18]。

2.3 重磁异常信号的非高斯性

同一高度二维规则网格点的重磁异常数据是由不同深度及不同尺度的地质异常体在该观测高度产生的重磁异常相叠加的结果。反之，同一高度二维规则网格点的重磁异常数据可以分解为多种深度以及多种尺度的重磁异常体在该观测高度产生的重磁异常。根据位场数据的叠加性原理，可以对重磁异常数据进行分场。但是，在应用ICA进行重磁异常分解之前，需要证明源信号具有非高斯性。

信号的非高斯性度量可以采用峭度系数K。当K=3时，表示信号为高斯分布即随机变量x具有零峭度；当K<3时，则为亚高斯分布即随机变量x具有负峭度；当K>3时，则为超高斯分布即随机变量x具有正峭度。对于本文使用的模拟重磁异常数据以及实际重磁异常数据(图2a3与图2b3、图7所示数据)，其概率密度曲线如图1所示。可见本文使用的模拟重磁数据与实际重磁数据均具有非高斯性，且根据中心极限定理，假定源信号的趋势场与局部场信号也具有非高斯性。此外，根据概率密度函数的定义以及重力异常数据与总磁场强度异常数据的特征，可以推知其在数据幅值极值点处的概率密度函数也一定位于极值点。对于实测的重磁异常数据，其概率密度估计函数的极值点个数一定不少于两个，由此可知其概率密度估计函数一定不符合高斯分布，从而证明实测信号为非高斯信号，这与其他学者所得结论一致[16,18]。

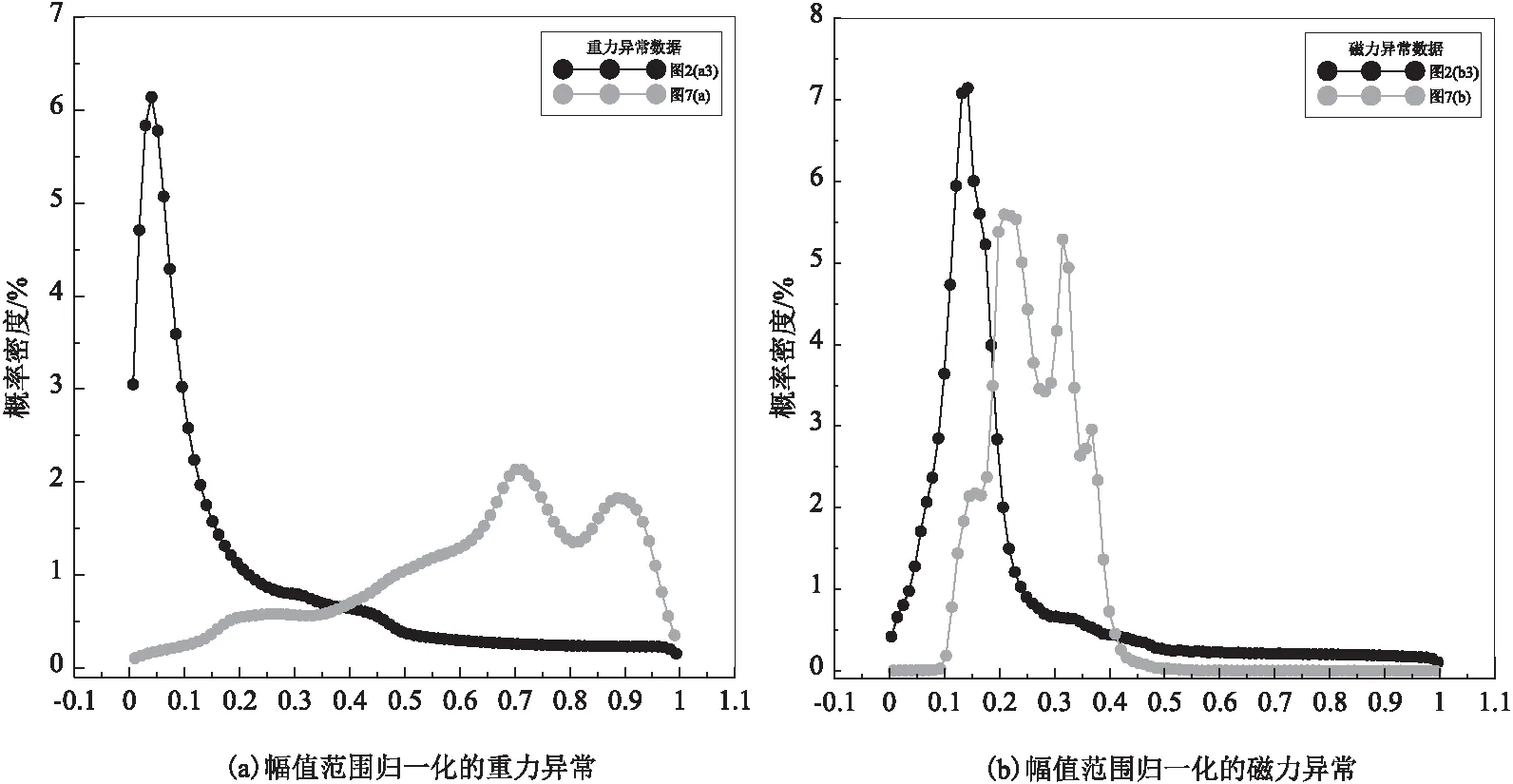
图1 重力异常与磁力异常的概率密度曲线

3 多道信号构建方法

ICA方法是一种多道信号分解方法，相对于主成分分析与奇异值分解等多道数据分解方法，ICA方法对于源信号的要求极为严格，即要求源信号之间相互统计独立，且具有非高斯性。所以，作为源信号线性叠加得到的ICA输入信号如何构建，是ICA方法能否有效应用于重磁异常信号分解中的关键问题。

3.1 相邻剖面法

相邻剖面法是可以用于ICA方法的多道信号构建方法之一，即利用相邻的两条同方向测线数据来构建多道信号。张念[16]与马龙等[18]使用相邻测线的重磁剖面数据构建多道输入数据，利用ICA方法进行重磁异常信号分场，实现了理论重力数据与实际磁测数据的多尺度分解。但这种方法实际操作较为繁琐，对二维数据进行分场需要不断地选择相邻剖面进行分解，且相邻剖面的重磁异常数据对应的是其下的地质异常体，位置还是有些许差异，属于不同的信号源，在使用ICA方法进行分解的过程中会引入一定的系统误差。

3.2 平移法或相空间重构法

平移法又称相空间重构法。对一个长度为M的初始信号，如果需要的多道信号个数为N个，则设置大小为M-N+1的信号截取窗口，从初始信号的首个数据开始，逐次向后平移一个数据长度，直到窗口位于初始数据的末尾。利用平移法，可以从长度为M的单道初始信号得到一个大小为N×(M-N+1)的多道信号矩阵，从而可对单道初始信号利用ICA方法进行分解。平移法常用于利用主成分分析和奇异值分解方法对地球物理时变信号的分解中[19]，本文尝试利用平移法进行ICA多道信号构建，并将其应用于重磁异常数据分解中。

3.3 空间延拓法

考虑到相邻剖面法与平移法的应用效果、效率与优缺点，本文提出利用对重磁数据进行频率域向上延拓的方法来构建多道信号。对于重磁规则网格平面数据，采用频率域二维延拓方法来分别构建多道信号[20,21]，从而可以利用ICA方法分别对数据进行分解。如果考虑不同高度的重磁延拓数据是由可近似的空间域固定延拓信号与不同尺度重磁场信号的线性叠加，则利用空间延拓法构建的多道信号与ICA方法对输入信号的要求及其算法原理相匹配。

4 基于仿真数据的对比分析

为了直观地展示三种多道信号构建方法在ICA平面重磁异常数据分离中的效果，建立理论模型，并进行正演得到模拟平面重磁异常数据，通过计算分离的局部与区域异常和理论的局部与区域异常之间的差异性，定量分析三种方法的重磁异常分离效果。

4.1 理论场源模型与仿真数据

平面重磁异常数据的正演模型为四个不同位置与尺度的长方体模型组合而成，其中深部设置一个高剩余密度与磁化率差异的大尺度长方体模型，浅部同一深度设置三个小尺度具有相同剩余密度与磁化率差异的低磁、低重长方体。其中，正演数据南北方向与东西方向长度均为15 km，测线方位角为0°，线距与点距均为100 m，设置异常体磁化方向与主磁场方向一致，主磁场强度为57 793 nT，主磁场倾角与偏角分别为67°与4°，主磁场参数与后文实际应用地区的地磁场参数一致。模型参数如表1所示，理论模型的重磁数据正演结果如图2所示。

表1 理论场源模型参数

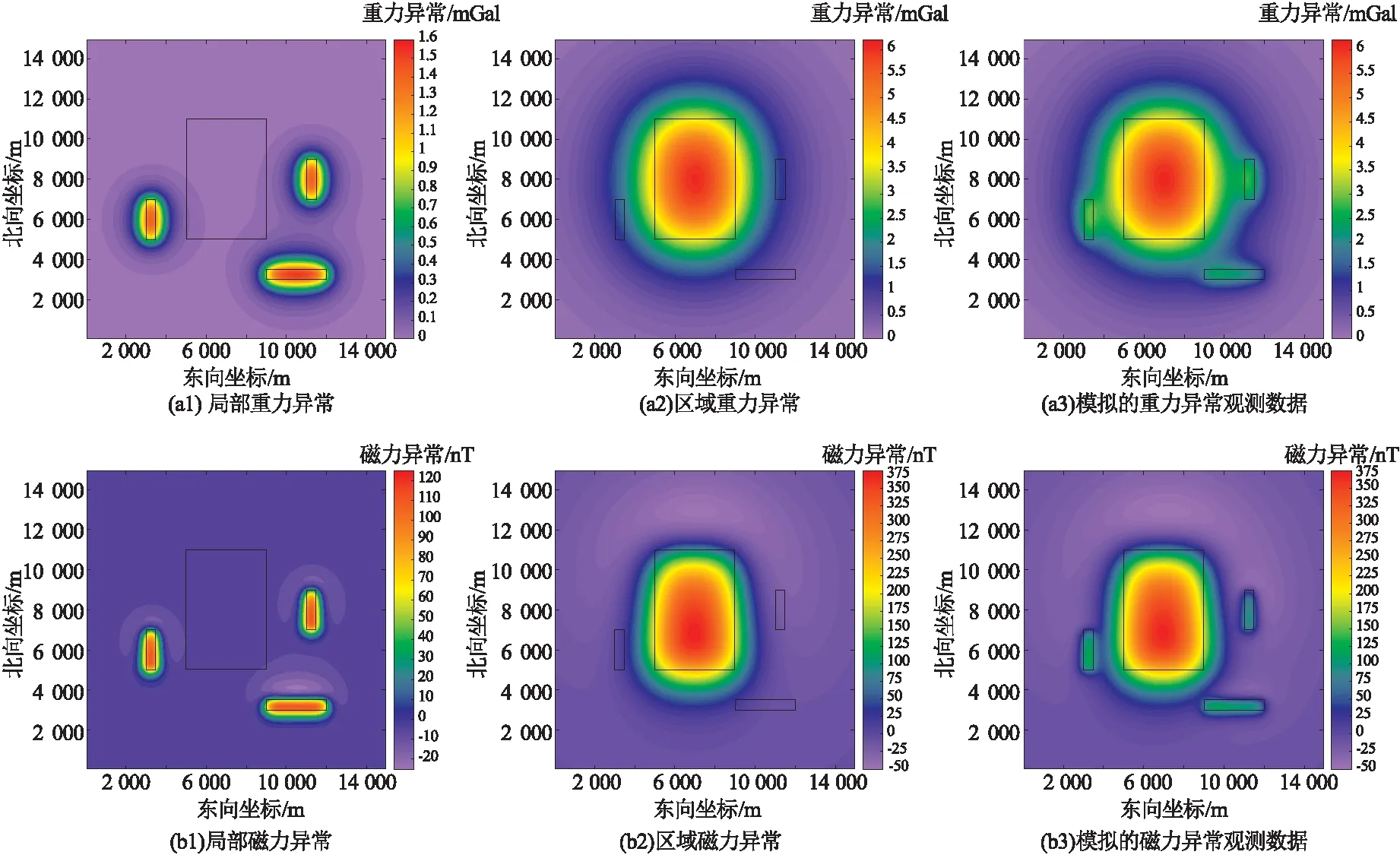
图2 仿真模拟的重力异常和磁力异常数据

4.2 异常分离结果的对比分析

利用相邻剖面法，连续选择平面数据中两条相邻的剖面数据作为ICA输入数据，每个输入信号的数据个数为150，进行ICA分解之后将分解结果进行拼接，由于每次ICA分解只有两道输入数据，因此无法计算其分解结果的累加贡献率曲线。

利用相空间重构法，首先将平面二维数据排列成为一维数据，且其信号长度为150×150，设置通道个数为10个，为了避免展开的一维数据还原为二维数据时不同通道的数据还原方式不同的问题，把平移步长设为一个测线长度(150个测点)，则信号截取窗口大小为150×(150-10+1)，从而获得一个大小为10×[150×(150-10+1)]的多道信号矩阵，这样既避免了过于复杂的数据还原的问题，又使多道信号矩阵内的数据遍历了整个原始数据。对多道信号矩阵进行ICA分解，得到分解结果的累加贡献率曲线如图3灰色点划线所示。由图3可知，对于重磁异常均将1阶模态对应的独立成分视为趋势场、2～10阶模态对应的独立成分视为局部场。

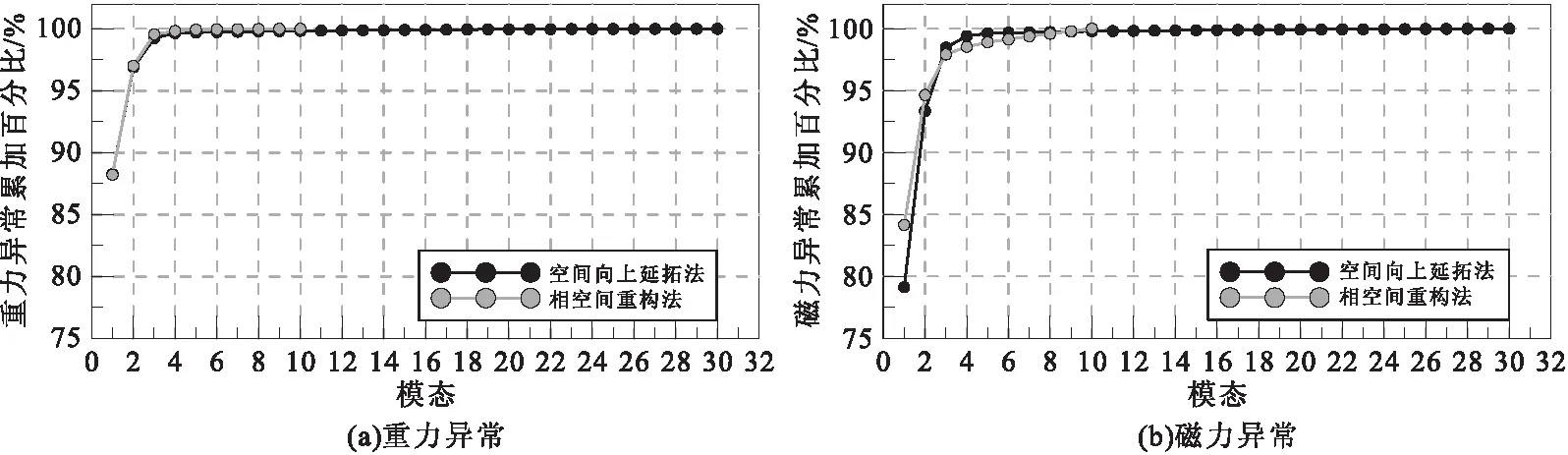
图3 仿真模拟的重力异常和磁力异常模态贡献率累加曲线

采用空间向上延拓法，首先对平面重磁异常数据在波数域按照测点点距等间隔向上延拓29个高度，获得30套平面重磁异常数据，分别将其排列成为一维数据，从而构建成一个30×(150×150)的多道信号矩阵，对其再进行ICA分解，得到分解结果的累加贡献率曲线如图3黑色点划线所示。根据图3，对于重磁异常也均将1阶模态对应的独立成分视为趋势场、2～10阶模态对应的独立成分视为局部场。

基于三种构建多道输入信号方法的ICA分解结果如图4所示。对比图4分离出的局部、区域重磁异常与图2所示的理论局部、区域重磁异常可以看出，基于空间延拓多通道信号构建方法的ICA分离效果明显优于其他两种方法，提取出的局部异常更加完整，受区域异常的影响更弱；此外，如图4所示，基于相邻剖面法的ICA分离结果存在1行数据丢失，而基于相空间重构法的ICA分离结果存在9行数据丢失，这是由于此类多通道信号构建方法本身的缺陷导致的。

图4 仿真模拟重磁异常的分离结果

5 实际应用

为了验证本文所提方法的有效性与实用性，首先对实际重磁资料采用向上延拓法构建多通道信号，再进行ICA分解，最后对分离结果与经典的匹配滤波法[23]分离结果以及地质资料进行综合分析。

5.1 研究区域概况

本文选取的研究区域为新疆维吾尔族自治区克拉玛依后山地区，主体处于西准噶尔区域加依尔山中段，东南部为准噶尔盆地，属于盆山结合部位。如图5所示，研究区地理坐标范围为东经84°～85°30′、北纬45°～46°20′，面积约为1.7×104km2。研究区域所属的西准噶尔山区地貌为中低山地貌，相对高差不大，山体之间镶嵌一些小型的盆地，地势总体西北高、西南低。

从大地构造角度看，克拉玛依后山既处于中亚大地构造带的核心位置，又位于几个次级板块的交汇地处，即塔里木板块、西伯利亚板块和哈萨克斯坦板块的汇合段。古生代期间特别是晚古生代期间经历了复杂的洋陆转换过程，残留了系列近东西向及北东向蛇绿构造混杂岩系以及古大陆边缘的增生体系，造就了测区复杂的岩石地层系统。在古生代洋陆转化过程以及后期陆内演化过程中，产生包括古洋盆、洋岛、俯冲岛弧、碰撞及碰撞后等多种不同类型构造背景下的岩浆活动和构造活动，形成测区复杂的侵入岩和火山岩体系；多期次的构造变形及其叠加改造也造就了测区复杂的构造变形格式。

研究区内侵入岩发育(图5)，从超基性岩至酸性岩均有出露，主要是晚古生代岩浆活动的产物。其中，中酸性侵入岩既有深成相的巨大岩基和中小型岩株，也有超浅成相的岩枝或岩脉。这些侵入岩的组成较为复杂，从闪长岩、石英闪长岩，到中酸性的花岗闪长岩和酸性的二长花岗岩、碱性花岗岩均有出露。研究区域的主要岩体为阿克巴斯陶、庙尔沟、红山、小西湖、夏尔蒲、克拉玛依、铁厂沟、哈图8个岩体，还发育玛里雅、达尔布特、白碱滩3条蛇绿混杂岩带以及大棍、哈图、克拉玛依3条构造混杂岩带，以及达尔布特断裂和哈图断裂等。其中，达尔布特深大断裂是研究区内最大的且最重要的一条构造带，该断裂北东-南西向延伸长约400 km，倾向北西，倾角80°近于垂直，断裂宽约1 km，是塔城盆地与准噶尔盆地的界限，具有平移走滑性质。

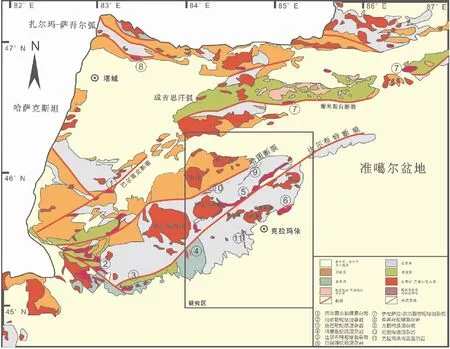
图5 研究区域的地理位置图与地表地质简图[22]

5.2 重磁异常数据

实际数据选取为克拉玛依后山地区布格重力异常数据(图7a)和化极处理之后的航空ΔT磁力异常数据(图7b)，空间分辨率均为500 m×500 m。研究区域布格重力异常具有中部山区高两边盆地区低的特点，与地势展布特征(中间高两侧低)呈负相关关系，整个异常高值区与达尔布特大断裂的展布方向一致，即呈NE-SW向展布，这也与该区域的构造走向一致，在盆山结合部位呈现为明显的重力梯度带。由于较强的背景异常掩盖了研究区内浅部不同地质体反映出来的异常特征，区内不同的岩体及蛇绿岩带的异常特征不能直接反映出来，因此需要进一步进行异常分离以突显局部异常特征。与重力异常相比，化极航空磁力异常的空间分布特征更加复杂，表现为在大面积正、负磁异常区块上叠加了复杂的局部异常，在铁厂沟北部的盆地地区表现为低磁异常特征，且与低重异常特征对应，在准噶尔盆地西北部表现为大面积高磁异常特征。除此之外，航磁异常没有表现出与地质构造明显的对应关系，因此需要进一步对其进行异常分离处理。

5.3 结果对比分析

为了提取图6所示的局部重磁异常，首先采用上延法构建了30套重磁异常数据，然后将平面二维数据排列成为一维数据，构成30道多通道信号，最后对其进行ICA分解，得到如图7所示的研究区域的布格重力异常与化极磁力异常模态贡献率累加曲线。

图6 研究区域的布格重力异常与化极磁力异常分布

图7 研究区域的布格重力异常与化极磁力异常模态贡献率累加曲线

由图7可以看出，研究区域的重磁异常可以分解为三套独立成分，即第1模态对应成分主要反映区域场特征，第2模态对应成分主要反映次级区域场特征，第3～30阶成分主要反映局部场特征。进而，对分解的三套独立成分进行重构，获得的研究区域布格重力异常与化极磁力异常ICA分解结果如图8所示。

图8 研究区域布格重力异常与化极磁力异常ICA分解结果

由图8可以看出，相比传统的局部异常和区域异常二分法，虽然ICA分解提取出了次级区域场成分(图8a2与图8b2)，但是分解结果具有一定的模态混叠效应，例如在第2模态对应的重磁异常中明显存在波长较短的局部异常，因此为了与传统分场方法对比，本文对2阶模态对应的重磁异常(图8a2与图8b2)进行了匹配滤波处理[23]，将其分离的区域和局部成分分别叠加于1阶模态对应的重磁异常(图8a1与图8b1)和3～30阶模态对应的重磁异常(图8a3与图8b3)中，从而获得最终分离出的区域与局部重磁异常，如图9(a)所示，笔者将此方法称为ICA-匹配滤波联合法。对比直接匹配滤波法分离结果(图9b)，可以看出，一方面匹配滤波法存在比较严重的边界效应(如图9b2)，另一方面ICA-匹配滤波联合法分离出的局部重磁异常相比而言具有更高的空间分辨率。

由图9可以看出，区域重力异常主要反映了基底埋深变化，且与地表地质单元分布比较一致；对于区域磁力异常，铁厂沟岩体北部的盆地区域为北东-南西向的低磁异常区带且与低重力异常特征比较一致，在克拉玛依后山表现为南北两个低磁异常区的分界，但是在准噶尔盆地西北部表现为高磁特征，这与18～26 km深度的高横波速度异常[24]一致，可能反映了古洋壳的高磁性特征[24,25]。

对于局部重磁异常，主要反映了岩体、蛇绿混杂岩带、结晶基底起伏等。在达尔布特蛇绿混杂岩带出露的地方表现为串珠状的高磁异常与低重异常；克拉玛依蛇绿混杂岩带并未表现出明显的高磁异常，而表现为带状低磁异常。研究区内出露多个性质不同的花岗岩体，主要成分为闪长岩、二长花岗岩、碱长花岗岩，其地质年代均在295 Ma～322 Ma之间，属于晚古生代石炭纪时期形成的[22]。根据各岩体的岩性物性不同，其表现出的重磁异常特征亦不相同。其中，以碱长花岗岩为主要岩性的庙尔沟岩体、阿克巴斯陶岩体、克拉玛依岩体主要表现为重力高与磁力低；以闪长岩为主要岩性的包古图岩体、柳树沟岩体主要表现为重力高与磁力高；以二长花岗岩为主要岩性体的小西湖岩体、夏尔莆岩体主要表现为重力低与磁力高；而红山岩虽然其岩性是碱长花岗岩，但是表现为重力低与磁力高，出现这种情况的原因是其与达尔布特蛇绿混杂岩带的位置较近，可能在深部随着断层倾向的变化二者发生接触蚀变，或者其岩性与小西湖、夏尔莆岩体一致为二长花岗岩。

6 结 论

1)结合ICA方法的基本原理与算法特征，为了更好地对重磁异常数据进行ICA分解，本文提出了基于相空间重构法以及基于空间延拓法的多道信号构建方法；

2)基于模拟数据，对比分析了相邻剖面法、相空间重构法与空间延拓法三种多道信号构建方法在重磁异常分离中的应用效果，结果表明基于上延法的多通道信号构建方法具有更好的应用效果；相邻剖分法仅适用于2D重磁异常，对于3D重磁异常其分解结果受剖面位置影响；虽然相空间重构法会丢失数据，但是理论上可以用于不规则分布数据；

3)在实际资料应用中，ICA方法虽然能够对重磁异常进行多尺度分解，但是各模态对应的重磁异常存在模态混叠效应。针对此问题，本文提出将ICA与匹配滤波相结合的联合法。实际分解结果表明，ICA-匹配滤波联合法不仅具有较弱的边界效应,而且分离出的局部重磁异常具有更高的空间分辨率，且分离的区域场、局部场和实际地质构造具有较好的对应性。

综上所述，ICA方法相较于传统的位场分离方法，其通过最大化输入数据源信号之间的统计独立性来对输入数据进行分解，在统计学角度，为研究位场分离问题提供了一种新的选择，且通过空间延拓方法构建ICA多道输入数据并进行ICA分解的位场分离结果也表明，该方法具有有效性与实用性，且在地下先验信息较少等特殊情况下，利用ICA方法分解重磁异常数据能够从一个新的角度为异常分离结果提供更好的参考。