黄土地层浅埋暗挖隧道松散围岩压力计算*
2022-08-10商学旋陈箐芮郑选荣叶万军
戴 俊,杨 康,商学旋,陈箐芮,郑选荣,叶万军
(1.西安科技大学 建筑与土木工程学院,陕西 西安 710054;2.陕西建工集团股份有限公司,陕西 西安 710003)
0 引言
围岩压力来源确定是地下洞室按照荷载-结构法进行衬砌结构设计的关键,是地下建筑结构课题研究的重点[1-2]。对于黄土地层浅埋隧道围岩压力的研究,主要通过理论分析、现场监测、模型试验和数值模拟展开[3-5]。目前,常用松散体围岩压力计算方法包括全土柱理论、岩柱理论、太沙基压力理论、谢家烋理论和基于岩柱理论的修正算法(比尔鲍曼理论)[6]。全土柱理论适用于埋深较浅的洞室或采用明挖法施工的地下工程,该理论不考虑开挖洞室跨度,认为围岩压力大小仅与洞室埋深有关,埋深较大时,全土柱理论计算的围岩压力偏于保守且计算结果大于实际压力;岩柱理论在全土柱理论基础上,考虑岩柱的应力传递、土体黏聚力、摩擦角以及朗金主动土压力系数[7],该理论所取岩柱宽度大于实际宽度,计算结果偏于安全;太沙基压力理论扩大开挖隧道上方岩柱范围,并假定岩体为散体,考虑土体的强度参数(c,φ)、埋深和隧道尺寸等对围岩压力的影响,但仅适用于围岩条件较差的隧道围岩压力计算;谢家烋理论将隧道开挖后的土体假定为隔离体,按照静力平衡法计算松散围岩压力,但该理论未考虑黏聚力且人为假定θ角对结果影响较大;比尔鲍曼理论考虑岩柱宽度减少和上覆土体强度(c,tanφ)折减,认为上覆土体给支护结构施加的围岩压力等于岩柱重力减去两侧破裂面上摩阻力。由于黄土具有垂直节理发育、土质疏松、遇水易崩解剥蚀等特性[8],利用比尔鲍曼理论计算围岩压力时,黄土的土体强度参数可考虑折减3倍[9],其理论值大于太沙基公式,与岩柱理论计算公式相近,但该理论易受围岩条件限制,使计算结果为负值。上述理论大多基于施工经验,由于不同地区岩土体力学参数差别较大,使围岩压力理论值与实测值误差较大。
鉴于此,本文通过对西安地铁2号线二期工程何家营暗挖隧道的破坏模式进行分析,将隧道开挖后的周边土体受力模式进行简化,按照静力平衡分析推导出适用于黄土地层浅埋暗挖隧道围岩压力的解析式,分析该公式适用范围,研究单因素改变对围岩压力的影响,并将新方法计算的围岩压力值、现场实测值和既有理论计算值进行对比分析,验证新方法的合理性和适用性。
1 隧道松散围岩压力计算方法
1.1 黄土地层围岩压力计算
根据施工现场既有情况,导洞周围存在多处微小裂缝,主要分布在导洞开挖面两侧,裂缝沿洞两侧斜向上扩展,直达横通道顶部,横通道顶部至地面段的微裂缝扩展无法观测。为防止导洞拱顶沉降过大而使裂缝继续扩展,在导洞内设置横向与纵向临时钢支撑,并对微裂缝进行注浆加固。导洞内临时支撑结构如图1所示,浅埋黄土洞室的破坏模式如图2所示。

图1 导洞内的临时支撑示意

图2 浅埋黄土洞室的破坏模式
假定AC,BD为隧道开挖后,隧道上方土体为达到稳定,受自身重力下滑而形成的破裂面,与水平面夹角为β。洞室开挖后,导洞施工区形成临空面,导洞上方土体EFHG受重力作用下沉,带动导洞两侧土体EAC,FDB下沉。由于斜面AC,BD提供的黏聚力和内摩擦角限制土体EAC,FDB下沉,导致土体EFHG下沉受到约束,最终土体ACBD达到极限平衡状态。因两侧三棱体和土体EFHG间接触面的土体强度参数未知,该滑面摩擦角θ由经验给出,且θ取值影响围岩压力计算结果的准确性[10]。
1.2 围岩压力计算推导过程
假设浅埋黄土洞室的破坏模式呈对称分布,洞室破坏范围内的土体强度参数也呈对称分布。因结构力学中正对称结构的反对称内力为0,故对称轴上不存在沿轴向的剪应力。为简化计算,取洞室破坏模式的1/2进行受力分析,如图3所示。

图3 洞室受力分析
为减少因三棱土体EAC与土体EMNG间滑面摩擦角θ带来的误差,对土体EAC与EMNG进行整体受力分析。取土体ACGNME进行整体受力分析,力的矢量图如图4所示。导洞开挖方向取1 m,根据图3~4建立力的平衡方程,如式(1)所示:
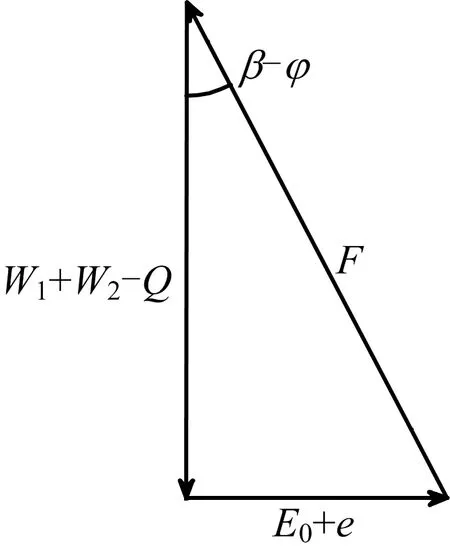
图4 力的矢量图
W1+W2-Q=(E0+e)cot(β-φ)
(1)
式中:W1为导洞上方土体EMNG的重力,kN;W2为三棱土体EAC的重力,kN;Q为作用在NG面上的垂直压力总值,kN;E0为中轴线上的静止土压力总值,kN;e为作用在支护结构上的侧向土压力总值,kN;β为滑动面AC与水平面的夹角,(°);φ为土体的内摩擦角,(°)。
土体ACGNME的自重如式(2)所示:
(2)
式中:γ为土体重度,(kN/m3);H为隧道埋深,m;B为隧道开挖宽度的1/2,m;h为隧道开挖高度,m。
作用在NG面上的垂直压力总值如式(3)所示:
Q=qB
(3)
式中:q为作用在NG面上的垂直围岩压力,kPa。
侧向土压力总值如式(4)所示:
e=λqh
(4)
式中:λ为侧压力系数。
静止土压力如式(5)所示:
(5)
式中:K0为静止土压力系数。
联立式(1)~(5)可得式(6):
(6)
整理得到作用在NG面上的松散围岩压力解析式,如式(7)所示:
(7)
若将q看作关于H的函数,则有式(8):
(8)
即隧道埋深为0时,作用在支护结构上的围岩压力不为0,这与实际情况不符,故对式(7)进行修正,得到作用在NG面上的垂直松散围岩压力解析式,如式(9)所示:
(9)
水平围岩压力解析式如式(10)所示:
qh=λq
(10)
式中:qh为支护结构上的水平围岩压力,kPa。
1.3 深埋和浅埋分析判据
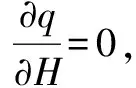
(11)
按极限平衡理论进行分析,隧道开挖后,土体ACGNME恰好处于临界平衡状态,隧道上方无垂直土压力作用,对应隧道埋深记为H0,故有式(12):
P=0⟺W1+W2-Fcos(β-φ)
(12)
根据图4所示三角形正弦定理,则有式(13):
(13)
简化后如式(14)所示:
K0Hcot(β-φ)=2B+(H+2h)cotβ
(14)
求解得式(15):
(15)
由此,当隧道埋深H∈(0,Hmax),作用在支护结构上的围岩压力随隧道埋深增大而增大;隧道埋深为Hmax时,对应作用在支护结构上的围岩压力取得最大值,此时隧道上方土体达到极限平衡状态,即隧道处于最危险状态;隧道埋深H∈(Hmax,H0),作用在支护结构上的围岩压力随隧道埋深增大而减小,这是因为土体力学性质随隧道埋深增大逐渐变好;隧道埋深为H0时,隧道上方土体恰好达到临界平衡,且无围岩压力作用到支护结构上;但隧道埋深H∈(H0,∞),新方法得到的围岩压力为负值,与实际情况不符,应选取适用于深埋隧道的围岩压力理论,故Hmax为隧道深浅埋的分界深度。式(15)得到的隧道深埋与浅埋分界深度主要由隧道开挖宽度B、高度h、土体内摩擦角φ和静止土压力系数K0确定。
2 围岩压力计算公式参数影响分析
以西安地铁2号线何家营站导洞暗挖段为工程背景,验证新方法的合理性。将新方法、全土柱理论、岩柱理论、太沙基理论、谢家烋理论以及比尔鲍曼理论随单一参数改变时的垂直围岩压力变化规律进行对比分析。其中,暗挖导洞开挖跨度为4 m、开挖高度为5 m的导洞暗挖段土层力学参数见表1。因采用新方法计算围岩压力时引入侧压力系数和静止土压力系数[11],该系数一般由经验公式得到,系数来源的准确性决定围岩压力计算结果的可靠性,且从现有围岩压力计算理论来看,围岩压力随隧道埋深变化易出现负值,即隧道埋深影响该理论的适用范围,需要通过对隧道埋深进行研究,以确定新方法的适用性[12]。

表1 导洞暗挖段土层力学参数
2.1 隧道埋深
对比隧道埋深变化对不同理论围岩压力值的影响,如图5所示。由图5可知,太沙基法和全土柱法的围岩压力随隧道埋深增大而增大;岩柱法、比尔鲍曼法、谢家烋法和新方法的围岩压力曲线呈抛物线形式变化,且先增大后减小;在围岩压力未达到峰值前,全土柱法的围岩压力值相对最大,新方法的围岩压力值相对最小,太沙基法的围岩压力值介于全土柱法和新方法之间,岩柱法、比尔鲍曼法和谢家烋法的围岩压力曲线非常接近,且介于全土柱法和太沙基法之间;当围岩压力大于峰值,谢家烋法的围岩压力衰减速率较大,岩柱法、比尔鲍曼法和新方法的围岩压力衰减速率接近,且小于谢家烋法;随隧道埋深增大,岩柱法、比尔鲍曼法、谢家烋法和新方法的围岩压力均会出现负值,与工程实际不符,此时应慎重选取围岩压力计算理论进行相关设计。何家营暗挖导洞埋深18.65 m,此时新方法计算的围岩压力比较接近峰值,隧道埋深较接近深浅埋隧道的临界深度Hmax(Hmax=20.98 m),但仍然小于临界深度,因此,在何家营导洞暗挖的埋深范围内,采用新方法计算围岩压力符合工程实际。
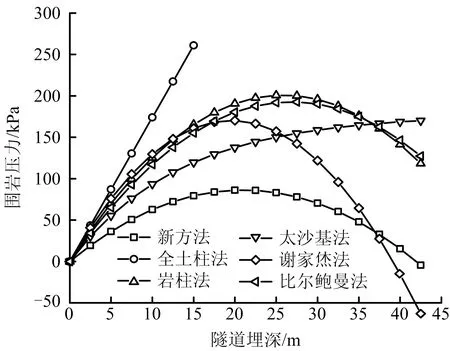
图5 隧道在不同埋深下的围岩压力曲线
2.2 侧压力系数
现有黄土隧道侧压力系数介于0.6~2.0[13],不同侧压力系数下的围岩压力曲线如图6所示。由图6可知,新方法和太沙基法的围岩压力随侧压力系数的增大逐渐减小,但新方法的围岩压力值小于太沙基法的围岩压力值。
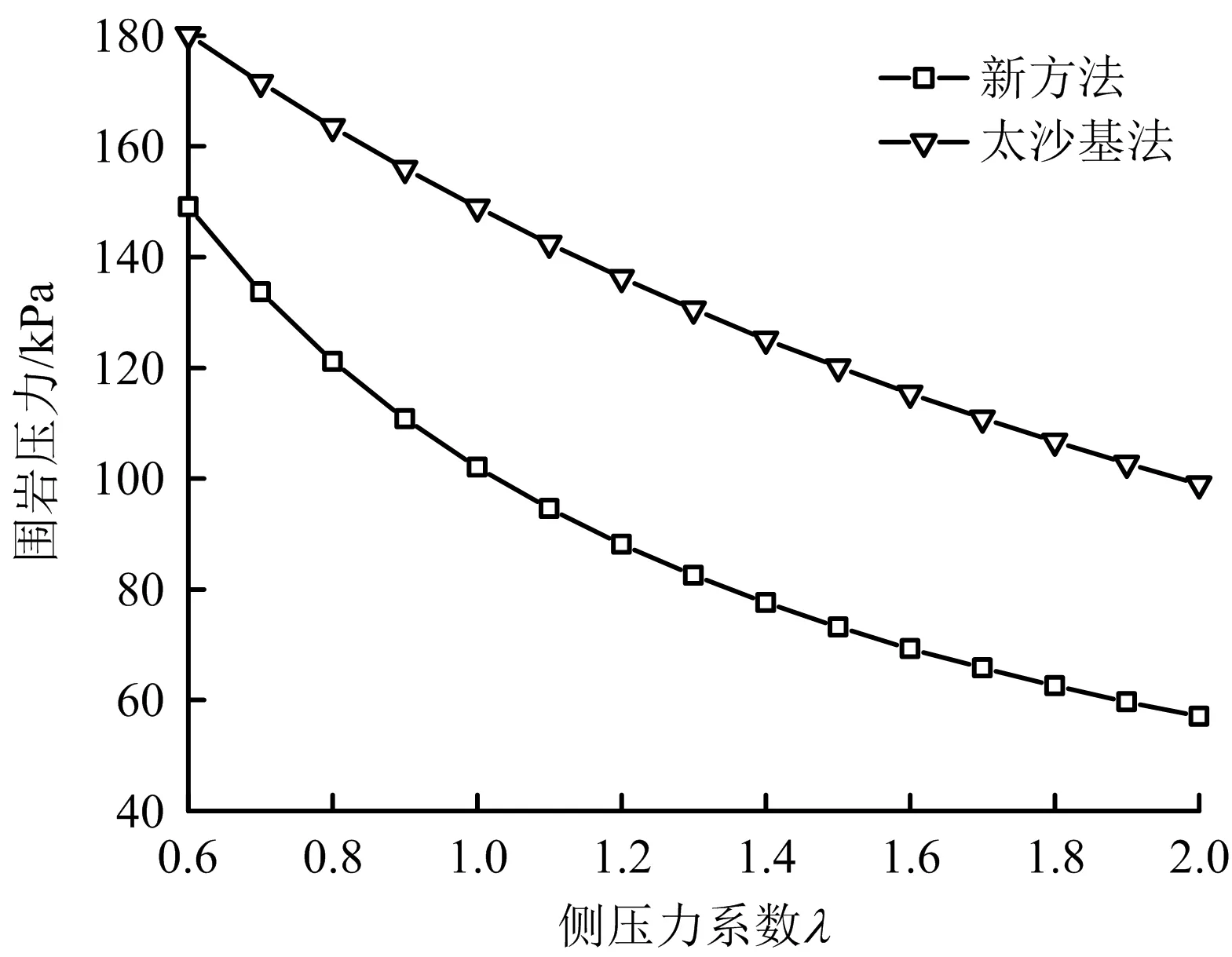
图6 不同侧压力系数下的围岩压力
新方法在侧压力系数改变时,围岩压力曲线呈反比例函数变化,当侧压力系数介于0.6~1.0时,新方法的围岩压力值随侧压力系数增大急剧下降,在该区间内,侧压力系数对新方法的围岩压力影响较大,应慎重选取侧压力系数;当侧压力系数介于1.0~2.0,随侧压力系数增大,围岩压力降低速率逐渐趋于平缓,表明侧压力系数越大且越接近2时,对新方法的围岩压力影响越小,这与太沙基法的围岩压力随侧压力系数变化规律类似。
2.3 静止土压力系数
静止土压力系数的确定对新方法的围岩压力计算至关重要。对于大型工程,一般通过现场试验确定静止土压力系数,包括室内K0试验、现场旁压试验或扁铲侧胀等原位试验[13-14];无试验条件时,一般采用Jaky[15-16]提出的正常固结土的静止土压力系数经验公式如式(16)所示:
(16)
式中:φ′为土的有效内摩擦角,(°)。
将式(16)简化得到静止土压力系数如式(17)所示:
K0=1-sinφ′
(17)
由式(17)可知,静止土压力系数与土的内摩擦角有关,且该系数取值介于0~1.0,但式(17)仅适用于砂性土[16],如何确定黄土地层的静止土压力系数比较困难。不同静止土压力系数下的围岩压力如图7所示。由图7可知,随静止土压力系数增大,新方法的围岩压力曲线呈线性趋势减小,当静止土压力系数大于0.83时,围岩压力计算值为负,此时新方法的围岩压力计算公式不再适用。

图7 不同静止土压力系数下的围岩压力
不同土压力系数下的围岩压力如图8所示。由图8可知,在单因素改变情况下,随不同类型压力系数增大,静止土压力系数K0改变下的新方法围岩压力值减小速率较大,侧压力系数λ改变下的新方法围岩压力值减小速率次之,侧压力系数改变下的太沙基法围岩压力值减小速率较小,即围岩压力受静止土压力系数的影响大于侧压力系数。采用新方法计算围岩压力时,静止土压力系数的选取应慎重,避免因参数选取不当带来的误差。
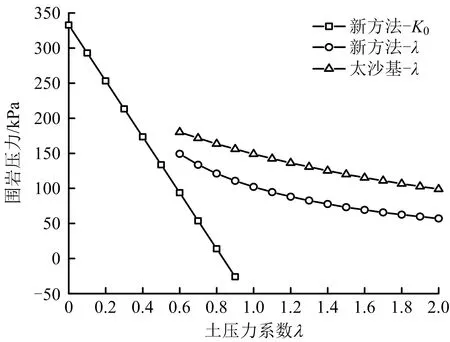
图8 不同土压力系数下的围岩压力
综上,在侧压力系数影响下,新方法和太沙基法计算的围岩压力均介于50~175 kPa之间,仅当静止土压力系数介于0.4~0.7时,新方法的围岩压力值在该区间内,故新方法中静止土压力系数的值介于0.4~0.7,符合黏性土的静止土压力系数取值介于0.5~0.7[17]的规律。
3 围岩压力计算值对比分析
将新方法的围岩压力值、现场实测值和既有理论围岩压力值对比分析,进一步验证本文推导的围岩压力计算公式的适用性。围岩压力现场实测值与不同理论计算值见表2,不同理论得到的围岩压力值与实测值误差如图9所示。
由表2和图9可知,无论垂直围岩压力还是侧向围岩压力,何家营暗挖导洞的现场实测值均小于不同方法计算的理论值。一方面因为隧道断面小且黄土直立性较好,隧道开挖后,围岩压力可能因土体自然成拱而减小[18];另一方面因为理论计算时存在较多理想化假设,计算中未能考虑土体颗粒间、土体与支护结构间相互作用,理论计算结果偏于保守。对于垂直围岩压力,全土柱法计算的围岩压力值相对最大,与其他理论值相比,误差高达83.16%;岩柱法、太沙基法、谢家烋法和比尔鲍曼法的围岩压力值偏大,且计算结果较接近,误差为63.33%~70.51%;新方法的围岩压力值相对最小且最接近实测值,与其他计算理论的围岩压力相比误差最小,为35.92%。对于侧向土压力,全土柱法的围岩压力值相对最大,误差高达85.15%;太沙基法的围岩压力值相对最小,误差为21.11%;而新方法与其他计算理论相比,误差仅次于太沙基法和比尔鲍曼法,且误差小于36%。本文计算的垂直、侧向围岩压力值均大于现场实测值,表明新方法在计算围岩压力并进行支护结构设计时,具有一定安全储备且更适用于黄土地层浅埋暗挖隧道的围岩压力计算。

表2 围岩压力实测值与理论值对比
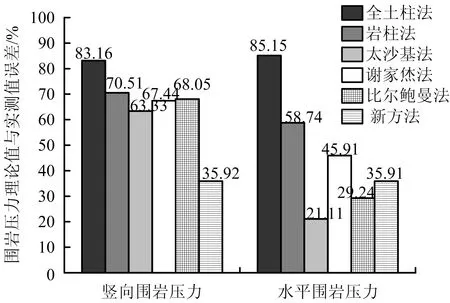
图9 不同理论的围岩压力值与实测值误差
4 结论
1)本文在已有围岩压力理论基础上,考虑侧向土压力、静止土压力、隧道尺寸、隧道埋深和土层参数对围岩压力的影响,基于极限平衡理论推导出适用于黄土地层浅埋隧道围岩压力的计算公式。
2)在新方法围岩压力计算公式基础上,确定深埋与浅埋隧道的临界埋深,且临界埋深主要取决于隧道开挖断面宽度、高度、土体内摩擦角和静止土压力系数等。随隧道埋深增大,新方法的围岩压力值曲线呈抛物线变化,呈先增大后减小的趋势。
3)新方法在计算围岩压力时,引入静止土压力系数和侧压力系数,在以上系数取值范围内,随静止土压力系数和侧压力系数增大,围岩压力计算值均呈减小趋势,但静止土压力系数对围岩压力的影响略较大。
4)对新方法计算的围岩压力值、既有理论的围岩压力值和现场监测值对比分析,现场监测值均小于新方法和既有理论计算的垂直、侧向围岩压力,但新方法计算的误差相对较小,可用于黄土地层浅埋暗挖隧道的围岩压力计算。
