基于近场动力学的煤体单轴压缩全过程损伤演化规律研究*
2022-08-10任天娇卞红杰
何 峰,任天娇,周 刚,卞红杰,杨 松
(1.辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000;2.陕西火石咀煤矿有限责任公司,陕西 咸阳 713599)
0 引言
地下煤岩体通常受到区域顶板及底板岩层的挤压作用,这与单轴压缩条件下的受力方向只在同一直线上,受单一作用力,产生压缩变形的载荷作用近似。基于此,导致煤体具有一定的初始损伤。由于在现场进行实验的困难,通过在真实岩石和类岩石材料上预先制造裂隙的室内模型进行单轴压缩实验研究裂隙岩体的破坏过程[1]。朱其志等[2]利用单轴压缩实验分析煤体受载内部裂纹扩展情况,得到裂纹均是在预制裂缝尖端首先产生,随后逐渐扩展贯通,最终导致试件的整体失稳破坏,煤体整体宏观力学性能劣化。但在分析煤样破坏时,采用的微分方程通常会发生求解不连续、位置偏导不存在的情况,由此导致分析困难。
近场动力学(Peridynamics,PD理论)作为1种新兴的非局部思想建立模型,通过求解空间积分方程来描述物质力学行为的方法;同时还兼有分子动力学方法、键基理论和无网格方式等多种分析手段,有效避免上述空间微分方程求解不连续的奇异性,突破在计算尺度上的局限,在宏观破坏与微观能量及键的断裂问题上均表现出很高的求解精度[3]。Silling等[4]提出的近场动力学方法通过损伤变量与空间积分方程来描述材料的损伤破坏情况,是1种非局部理论算法,从理论上克服局部计算时对计算网格的依赖,并总结岩体裂纹尖端部分数值模拟方案和内部能量来源及扩散情况;黄丹等[5]概述PD方法的理论基础、建模思路等,并介绍PD方法在不同尺度上、非连续力学问题中,均匀与非均匀材料和结构的大变形、损伤、断裂、冲击、穿透和失稳问题的应用。继而出现了很多关于函数的构建、裂纹损伤的数值模拟以及算法优化的研究。PD理论用于分析工程材料断裂过程中的裂纹扩展问题,构成该理论的本构关系—用键的断裂表示材料断裂[6]。从理论上克服局部化方法存在的数值结果对计算网格的依赖性。
基于上述研究,对煤体破坏全过程裂纹扩展情况进行单轴压缩实验,根据近场动力学与损伤变量演绎推导PD损伤本构力函数,进而基于PD损伤本构力模型分别在宏、微观2个方面对煤体损伤规律进行探讨,根据所构建的本构力函数模型来进行lammps软件数值模拟,比对室内实验与模拟结果来研究煤体损伤过程及损伤规律。
1 实验
1.1 煤体制备与实验
样品取自于陕西火石咀煤矿有限责任公司,共3组煤:1组靠近煤层顶板、1组为煤层中部、1组靠近煤层底板,煤样加工为50 mm×50 mm×100 mm的长方体。每种煤样进行5次实验。通过万能拉伸实验机对不同煤样进行单轴压缩实验,以0.05 mm/s的位移速率加载直至煤样破坏,由于实验中,部分试件裂纹不明显或煤样破碎,无法进行更进一步的研究,所以本次研究主要分析3组中最优煤样。其压缩前、后对比如图1所示。
根据图1可知,煤样都会经历压密阶段、弹性阶段、屈服阶段以及破坏阶段。实验开始时,煤样处于微压力初值阶段,紧接着煤样进入稍微压密阶段,随后煤样微节理逐渐稳定;压力逐渐增加,煤样内部微节理开始扩展;随着压力的进一步加大,煤样在微裂纹的基础上迅速扩展,导致煤样开裂;最后压力增大导致微裂纹相互贯通,煤样破坏。
卸载后,分叉裂纹开始完全贯通,形成十字交叉的主裂纹,同时有多条新的裂纹出现,试件彻底破坏。煤样裂纹形式以“X”型裂纹以及“Y”型裂纹为主,同时伴有其他微裂纹的产生及扩展。
1.2 结果分析
煤体材料内部存在不同角度、不同尺寸、不同形状的孔隙、裂隙。原生微裂隙的存在使煤体宏观力学特性表现为非线性、非均匀的特点。研究表明,应力-应变曲线能够很好地反应材料损伤状况,而岩石应力-应变曲线可分为弹性阶段、塑性阶段、峰后软化阶段和残余应力阶段,这是岩石类材料压缩过程中常见现象[7]。实验所得煤样应力-应变曲线与岩石类材料全应力-应变曲线对比如图2所示。
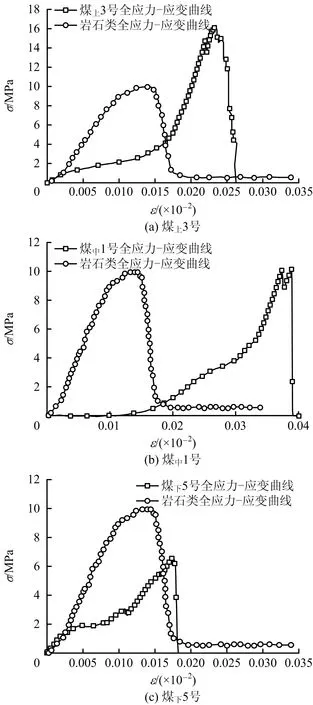
图2 不同煤样应力-应变曲线
根据图2,不同煤体的损伤与岩石类材料的应力-应变曲线有很好的对应性。另外轴向应变的变化过程大致分为:达到峰值→短暂下降→急剧上升→垂直下降。这种变化现象其实是岩石类材料的相继屈服现象,当煤体试件初始屈服后,随着应力和变形的增加,屈服应力不断提高(应变硬化或强化)或者提高到一定程度后降低,这是一般煤体试件压缩过程中常见的现象。煤样的垂直应力σ越大垂直应变εy就越大,损伤变量越大煤样的破碎效果表现得越好。继而煤体的受力破坏过程,即其内部裂隙和节理的产生、发展的过程越快。
2 近场动力学(PD)理论
2.1 PD理论
PD理论是在传统连续介质力学基础上对固体力学中的运动方程的重新描述,该理论的积分方程代替传统力学中微分方程,应用于求解非连续位移处,避免了微分方程出现奇异解的问题。与传统的连续力学相比,PD理论是物质点在其邻域内与其他物质点之间发生相互作用。可以描述位移的连续、非连续变化;模拟非连续位移处裂纹的损伤扩展过程。同时PD理论具有其本身自己的破坏准则,在求解损伤破坏问题时,无需引入其他的破坏准则,通过求解积分方程的方式描述物体的整个损伤断裂过程,裂纹可以沿任意方向扩展。因此,PD理论在求解非连续问题时展示出其独特优势,能够精确模拟复杂的损伤和裂纹扩展过程[8-9]。
将空间R离散为点单元,其中某质点x在t时刻的基本方程如式(1)所示:
(1)
式中:ρ(x)表示t时刻质点x的密度,g/cm3;ü(x,t)表示t时刻质点x的加速度,m/s2;u(x,t)与u(x′,t)表示物质点x与x′的位移,m;b(x,t)表示物质点x受到的外力,MPa;函数f是点x与x′之间的相互作用力函数,仅与物质点对x与x′之间键的变形有关[10];H为位置点的作用域。
根据式(1)可知,物质点x与x′在t时刻分别产生u(x,t)与u(x′,t)的位移,2质点在初始时刻的相对位置向量表示为:x′-x=ξ,并经过时间t之后2点间的相对位移向量为:u(x′,t)-u(x,t)=η,所以发生变形之后的相对位置向量为:ξ+η。此时,物质点x在区域内其他点的共同作用下而保持运动状态或平衡状态,其示意图如图3所示。
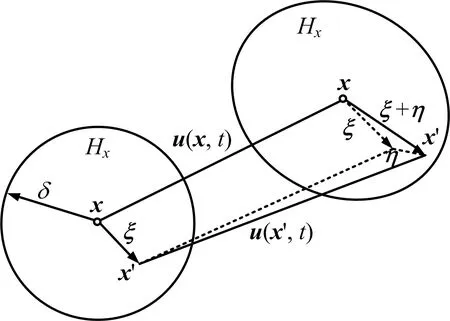
图3 近场动力学原理示意
PD理论中使用的积分方程替代传统力学中的微分方程,避免在非连续位移处导数不存在的问题,解决了煤体在损伤失效过程中产生的非连续问题。PD模型其中一种特例就是键基近场动力学模型,在该模型中,假设物质点之间的力密度矢量仅与物质点之间相对位置有关,而与物质点近场区域内的其他物质点变形无关。2物质点之间存在大小相等、方向相反、满足牛顿第三定律的力密度矢量,根据这种特性,键基近场动力学模型在保证计算精度的准确性情况下会一定程度上减少计算量,在解决复杂裂隙扩展方面尤为突出,其理论示意如图4所示。

图4 键基PD模型示意
该理论将模型区域离散成有限的物质点,在以δ为半径的近场区域H内物质点间存在着相互作用力——近场力。
其中,Hx是x的δ领域(近场区域的大小),是Hx内的点,定义在与物质点x距离为δ以内的点才会与其中心点x发生相互作用,与x有相互作用的点可以用集合Hx表示,如式(2)所示:
(2)
通过键的断裂,PD理论能够完整地模拟煤体的全部损伤失效过程。键破坏模式表示在1个物质点对内,相互作用的2个物质点间经过一定的相对位移后,当点对之间键的伸长率s超过临界伸长率s0时,该点对破坏,2物质点间不再有相互作用,将发生损伤。键的断裂和裂纹的关系示意如图5所示。

图5 键的断裂和裂纹的关系示意
若将物质点对键看作中心弹簧的铰接杆单元,可得本构力表达形式如式(3)所示:
(3)

(4)
近场力与键伸长率的关系如图6所示。当键的伸长率s超过s0时,键发生断裂,物质点之间不再存在力的作用。

图6 近场力与键伸长率关系
由于键型PD模型本构力函数包含损伤和断裂条件,不需要引入其他的破坏准则,如传统的临界应力强度因子等,运动方程中通过把力密度矢量用不可逆的方式表达损伤,荷载会在物质点之间产生重新分配,导致宏观损伤以自动发展的方式逐渐扩展。因此,在分析破坏问题时不必进行传统的开裂判断和裂纹路径等分析,裂纹将自然萌生并扩展。修正后的f(η,ξ)函数很好地体现了“近场”的思想,在近场范围内物质点对之间存在相互作用。现有的损伤模型和方程都是在静态实验条件下完成,得到的大多是宏观的规律,缺乏可靠的微观实验基础[11]。该模型中,本构力函数f与物质点对的伸长率s线性相关,这里的伸长率s可以看作是连续介质力学中的“应变”,故该模型可以用于宏观领域,即能在微观和宏观上达到统一。
2.2 脆性材料本构力函数模型
前苏联学者Kachanov[12]定义的损伤变量如式(5)所示:
(5)
式中:D为损伤变量;A*为煤体受损后损伤面积,m2;A为煤体初始无损横截面积,m2。
根据PD本构力函数f和损伤变量D通过数学拟合得到式(6),脆性材料本构力函数曲线如图7所示。

图7 脆性材料本构力函数曲线
(6)
式中:sc,st分别为断裂时的压缩率和伸长率,即当伸长率s超过断裂临界值时,材料将发生破坏;s0c,s0t分别为临界压缩率和临界伸长率,即压缩或拉伸状态下煤体试件不会产生裂纹的最大伸长率;sec,set分别为弹性压缩率和弹性伸长率,当sec≤s≤set时,材料受拉压表现为弹性性状,在不受力时,材料会恢复原状。
由图7可知,阴影区为键的损伤演化阶段,呈非线性。②,③阴影区分别表示材料在受拉伸或压缩时产生部分键的断裂并伴有微裂纹的产生;①,④阴影区分别表示材料在受拉伸或压缩时,产生键的断裂并有宏观裂纹的产生和扩展。在该模型中,物质点之间的作用力随着伸长率增大先增大后减小,力在到达临界伸长率时键发生破坏,而不是到达峰值作用力时突然发生破坏,符合岩石类材料先应变硬化再应变软化的变形机制[13-14]。
在式(6)伸长率s与键的损伤变量D关系中,当伸长率小于线弹性伸长率时,键不会出现变形断裂;当伸长量大于弹性伸长率时,键的损伤会随着伸长率呈指数增长直至断裂,键的断裂意味着裂纹的形成。具有线性和非线性的力学行为的本构力函数的基本形式如式(7)所示:
(7)
式中:s可根据物质点的相对位移η和相对位置ξ求出。
由于煤体受到外荷载作用后内部微结构会产生不同程度的损伤,损伤产生过程中必然有不同程度上微观的键的断裂。因此,在PD理论的基础上,结合损伤变量改进PD模型,进而对煤体损伤规律进行探究和总结是可行的。
3 数值模拟
以近场动力学的角度利用lammps原子分子并行模拟器来模拟并建立无网格的PD离散型模型,对于岩石类材料的冲击模拟,将模型设定为50 mm×50 mm×100 mm的长方体试样。密度、泊松比、弹性模量等材料参数均使用数值软件所定义的参数。为便于计算,将总时间步设定为20 000步。将模拟试样离散为250 000物质点,物质点间距为Δ=0.1 mm,δ=3.015Δ[15-16]。下边界固定,上边界以0.1 mm/min的速度施加均布荷载,为了使模拟结果更为准确,增加驰豫时间以卸载初始应力使模拟试样从激化的状态回复到平衡排列状态,强化驰豫过程,观察其裂纹扩展及内部能量的转换情况。
在模拟过程中采用PD模型来模拟岩体材料的力学特性,采用式(1)作为数值软件中的动力学控制方程,式(7)作为本构力函数。
利用compute stress/atom命令所计算出来的应力是通过对Virial定理所定义的体系应力按原子分解,即将Virial定理中按原子求和的算符删除(同时应将体系的体积换为单个原子的体积)。但由于单个原子的体积计算太麻烦,所以lammps计算时直接去掉了体积项,导致所算出来的“应力”具有能量的单位。因此,所输出应力需经过换算才能与实际符合,利用“compute v all voronoi/atom”等命令进行后续换算,对原子应力进行Voronoi体积加权平均即可得到系统瞬时应力,系统瞬时应力的系综平均值为宏观测量的系统应力值。换算后煤体内部产生破坏的最大应力约为0.1 MPa。经过后续可视化等分析处理可以得到模拟结果,如图8~11所示。

图8 压力闭合阶段模拟损伤云图
第1阶段:压力闭合阶段。由图8可以看出,模拟开始时,模型处于压密阶段,模型内部微裂隙、微孔隙逐渐闭合,模型所能承载的最大应力主要集中在模型中部位置,边缘位置应力较小,煤体模型中部出现了应力集中的现象。此时,模型中部位置发生轻微变形,宏观表现不明显。


图9 线弹性变形阶段损伤云图
第3阶段:非线性变形阶段。由图10可以看出,模型应力分布逐渐稳定,呈“X”分布。随着压力逐渐增加,模型内沿着应力分布区域大量的键发生断裂,模型产生损伤。此时模型宏观表现出有裂纹的产生,伸长、汇合、交叉、贯通,主裂纹呈“X”状,并在主裂纹附近有很多微小裂纹产生。从煤样宏观角度分析,大量裂纹迅速扩展,出现“X”型裂纹,导致模型开裂,裂纹走向及形状基本稳定。

图10 非线性变形阶段损伤云图
第4阶段:宏观破坏阶段。由图11可以看出,随着压力的增大,“X”型裂纹内所积聚的应力达到极限状态,无法继续承载多余应力,微观上表现为“X”型裂纹周围键全部断裂,多余应力贯彻遍布整个模型,宏观上损伤演化加剧,达到屈服应力,裂纹继续发展、交叉、相互汇合、贯通,导致试样破坏。

图11 宏观破坏阶段损伤云图
图8~11可以直观反映煤体试样损伤破坏全过程,试件微观键基变形损伤规律、应力扩散情况、宏观裂纹扩展情况能够较好地对应。宏观裂纹的萌生与扩展是微观键的断裂的外在表现,微观上键的断裂是宏观裂纹发生的内在原因。根据模拟方案,模拟煤体在单轴压缩条件下其内部应力-应变变化趋势,模拟应力-应变曲线如图12所示。
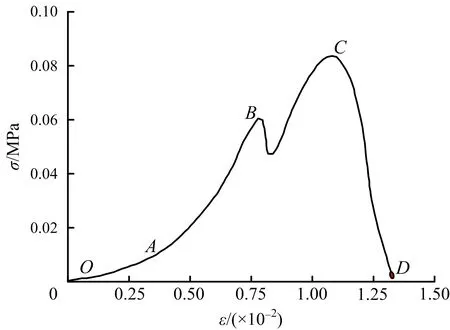
图12 模拟应力-应变曲线
与实验结果对比,实验结果曲线与模拟曲线走势大体相同,在受压闭合阶段及线弹性阶段均有回弹,表明在受压过程中均有弹性变形的发生与恢复,该阶段不发生损伤。在进入非线弹性阶段后应力突然下降,即大量键产生断裂,导致试样产生“X”型宏观破坏,此时试样发生损伤。印证了实验的准确性与模拟的真实性,说明近场动力学能够反映煤体的物理力学机制,并且作为一种脆性材料,煤体的本构关系与所构建的脆性本构力函数关系相同。
4 结论
1)煤体受到外荷载作用后内部微结构会产生不同程度的损伤,损伤产生过程中有不同程度上微观的键的断裂。利用演绎推导出的本构力模型来反演煤体内部微结构变化从而得到煤体损伤规律切实可行。
2)煤体损伤过程可分为:压密阶段、微裂纹的萌生扩展阶段、断裂破坏阶段3个阶段,除受压闭合阶段其余阶段均伴随键的断裂,至破坏阶段时,键几乎完全断裂,导致煤样失稳破坏。
3)模拟实验中,模型在受到外载荷作用下,内部能量开始聚集,随着压力的增大,内部能量散开,最终呈“X”型分布,这与实验加载后煤样的损伤效果基本一致,可为地下采煤及冲击地压防治提供理论支撑。
