基于马尔科夫链-多目标模型的应急供应链决策优化研究*
2022-08-10陈伟炯董雯玉李咪静张善杰李晓恋康与涛
陈伟炯,董雯玉,李咪静,张善杰,李晓恋,,康与涛
(1.上海海事大学 物流科学与工程研究院,上海 201306;2.上海海事大学 物流供应链风险控制研究中心,上海 201306;3.上海海事大学 海洋科学与工程学院,上海 201306)
0 引言
突发灾难事件频发,严重影响人类生活、社会稳定和经济发展。国家应急管理部数据显示,2020年我国自然灾害以地质灾害、洪涝为主,全年受灾人群达1.38亿人,死亡及失踪人数共591人,造成直接经济损失3 701.5亿元[1]。2020年新冠疫情曾造成口罩、防护服等相关应急医疗物资短缺,严重威胁公众生命安全。应急救援亟待低风险、高效率的应急供应链。
目前,应急供应链风险分析与应急物资优化调度成为国内外研究热点。在应急供应链风险分析方面,研究趋势逐渐由静态向动态转变,动态研究能够更加真实、客观地反应供应链风险及其变化。一方面,学者基于马尔可夫过程、混合数学规划、动态贝叶斯网络、鲁棒控制优化等[2-4]方法构建动态应急供应链模型,在灾情更新情况下分析供应链中的潜在风险,为应急管理提供实时有效的政策调整建议。另一方面,单一目标的应急物资调度规划模型已无法满足应急管理实际需求,因此,部分学者聚焦于多目标规划模型的研究,包括以最小化延迟时间、最小化运输成本或系统损失的双目标规划模型[5-6],在此基础上考虑最大化线路可靠性[7]、最大化供应链可视性[8]、最小化物资短缺[9]等因素的3目标优化模型。为有效提高应急供应链中断响应效率,学者展开应急供应链决策优化研究,基于可持续性、鲁棒性、韧性等,设计优化应急组织配置策略[10]、协同优化方法[11]、韧性优化策略[12],增强应急供应链恢复力,高效地应对风险,降低灾害损失。
在应急供应链风险动态变化基础上,现有研究对应急物资的多目标规划与决策优化的综合性研究尚有不足,且在算法求解上仍有改进空间。因此,本文提出离散时间马尔科夫链—多目标规划模型(DTMC-MOP),综合考虑供应率、时间、成本3个因素,动态识别、分析、应对应急供应链风险,并采用改进自适应NSGA-Ⅱ算法优化求解模型,以实现应急物资的最大满足率供应、最短时间供应和最低成本供应目标,研究结果可为及时控制灾情和最大限度地降低灾害损失提供参考。
1 DTMC-MOP应急供应链模型的构建
突发灾难事件发生时,应急供应链易受内外部不同程度的风险扰动。为保障应急救援工作的顺利开展,构建由应急管理部门、供应商、制造商、需求方组成的4级动态应急供应链网络,基于离散时间马尔科夫链(DTMC)模型,将状态转移概率及平稳概率分布引入多目标规划(MOP)模型,构建供应物资满足率最大、供应时间最短、供应成本最低的DTMC-MOP模型。
1.1 基于离散时间马尔科夫链的应急供应链模型
1)定义
①离散时间马尔科夫链
若随机序列{Xn,n=0,1,2,…}为状态离散的随机过程,其中状态空间I={i0,i1,…,in,j},时间集合T={0,1,2,…},如果对于任意状态满足式(1):
(1)
则称{Xn,n=0,1,2,…}是离散时间马尔科夫链[13]。
②k步转移概率及矩阵如式(2)所示:
(2)

(3)
③平稳概率分布
若分布概率π=(π1,π2,…,πj)满足式(4):
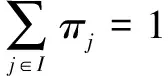
(4)
则称分布概率π是{Xn}的唯一平稳概率分布。
2)DTMC应急供应链模型
突发灾难事件是1个随机过程,且应急供应链的下一种状态仅和当前状态有关,具有马尔科夫性。通过DTMC模型动态描述应急供应链所处状态,直观反映应急供应链的运行状况。
考虑到供应链的韧性特征,即受到风险扰动导致供应链部分失效时仍能维持供应状态,并以最快的速度恢复到正常供应状态的能力。假设应急供应链在t时刻处于受不同程度干扰的有限个离散状态,由于供应链具有韧性,在t+1时刻可以向其他状态转移或保持该状态不变。当发生风险扰动时,假设应急供应链存在以下4种状态:状态0即完全吸收干扰的正常供应状态;状态1~3分别表示受到30%,60%,90%干扰的供应状态。任意2个状态之间可相互转移,用α1~α6和β1~β6(αi,βi≤1,i=1,…,6)表示状态转移概率。应急供应链DTMC模型如图1所示。
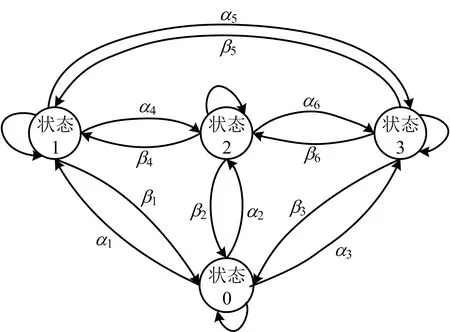
图1 应急供应链的DTMC模型
由图1可知,若t时刻供应链处于状态1,则在t+1时刻分别有β1,α4,α5的概率向状态0,2,3转移,有1-β1-α4-α5概率保持状态1;在t+2时刻,可从t+1时刻的状态转移至其他状态。根据式(2)~(3),该模型的状态转移概率矩阵Pij如式(5)所示:
(5)
通过了解应急供应链中每个状态的转移概率,能够动态识别、分析、应对风险。当供应链状态逐渐向中断状态(状态3)转移时,能够及时提醒供应链节点企业制定或修改应急措施,以减轻干扰风险;当供应链状态逐渐向正常供应状态(状态0)转移时,能够体现出供应链的韧性特征,并验证应急措施的有效性。
1.2 基于DTMC-MOP的应急供应链模型
突发灾难事件的发生具有不确定性和突发性。当发生突发事件时,灾区的应急物资需求量会急剧增加,在此之前相关部门应急物资的储备量远小于需求量,因此,需要将应急生产纳入考虑范围。应急供应链具有不确定性、强时效性和弱经济性等特征,为制定高效的应急物资供应方案,本文提出DTMC-MOP模型,研究供应率、时间和成本3方面因素对应急供应链的影响。
1)模型假设
由于应急供应链涉及多个供应环节及多个节点企业,为简化模型且不失一般性,本文提出以下3点假设:
假设1:应急供应链在0时刻处于状态0,在t时刻进行第1步状态转移,在t+1时刻进行第2步状态转移,直到得到平稳概率分布,结束状态转移。
假设2:制造商没有原材料和产品库存,应急物资是收到供应商提供的原材料后进行生产制造,而后通过应急物流送往需求地。
假设3:模型仅考虑原材料、应急物资的生产时间和运输时间,其他耗时忽略不计。
2)DTMC-MOP模型
I为供应链状态i的集合,i∈I(i=0,1,2,3);T为时刻t的集合,t∈T(t=0,t+1,…);D为需求地d的集合,d∈D(d=1,2,…);S为供应商s的集合,s∈S(s=1,2,…);M为制造商m的集合,m∈M(m=1,2,…)。
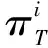
(6)
(7)
(8)
(9)
(10)
(11)

(12)
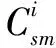
在DTMC-MOP模型中,式(6)描述最大供应物资满足率目标,即最小化物资需求未满足率;式(7)描述最短时间供应目标,即最小化原材料运输时间、应急物资生产、运输时间的总和;式(8)描述最低成本供应目标,即最小化供应商原材料成本和运输成本以及制造商物资生产和运输成本;约束(9)表示制造商M向需求地D供应物资的数量不超过需求地的物资需求数量;约束(10)是需求地D的物资需求满足率公式,它等于物资的实际供应数量除以需求数量;约束(11)是离散时间马尔科夫链中平稳概率分布公式;约束(12)表示决策变量为正整数。
2 改进NSGA-Ⅱ算法模型及评价
2.1 改进NSGA-Ⅱ算法模型
对于多目标规划问题的求解,国内外学者进行大量研究,比较常见的求解方法包括将多目标转化为单目标的精确算法[14-15]以及粒子群算法、模拟退火算法、遗传算法等智能算法[16-18]。与前人研究相比,本文将采用收敛速度快、计算精确度高、计算复杂度低的NSGA-Ⅱ算法求解模型,但该算法在搜素性能、种群多样性方面仍存在不足,为避免陷入局部最优,本文通过改进传统NSGA-Ⅱ算法,进一步适应应急供应链风险快速、准确响应并决策的特性,提升算法的收敛速度和搜索能力。改进自适应NSGA-Ⅱ算法流程示意如图2所示。
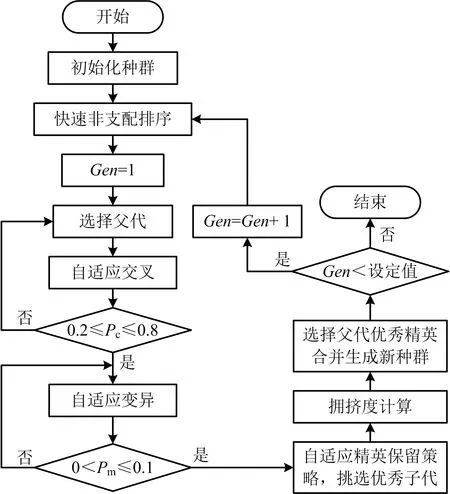
图2 改进自适应NSGA-Ⅱ算法流程
1)初始化种群改进
在应急供应链实际应用中,初始数据较大且关系构造复杂,本文通过以下3个步骤对数据及编码方式进行改进处理:
①采用实数编码方式对初始自变量进行处理。
②运用反编译将数据编码范围限定为0~1的随机数乘以基数的形式,可以大幅提高算法的运行速度。
③对反编译后的数据进行归一化处理,构造种群规模N的初始种群E0。
2)自适应遗传算子改进
①自适应多点交叉
在锦标赛选择中得到N个新个体中随机选择2个个体进行多点交叉,算法中交叉点的位置和数量是随机产生的。为避免陷入局部最优,本文采用自适应交叉法进行调节,从而大幅度提升算法的全局搜索能力。交叉概率Pc如式(13)所示:
(13)
式中:pfmax是该种群中适应度最大值;pf′为2个个体中适应度较大的值;pfmean为种群中平均适应度。
②自适应变异
随机选择交叉后的个体及基因位置以Pm的概率进行变异,如式(14)所示:
(14)
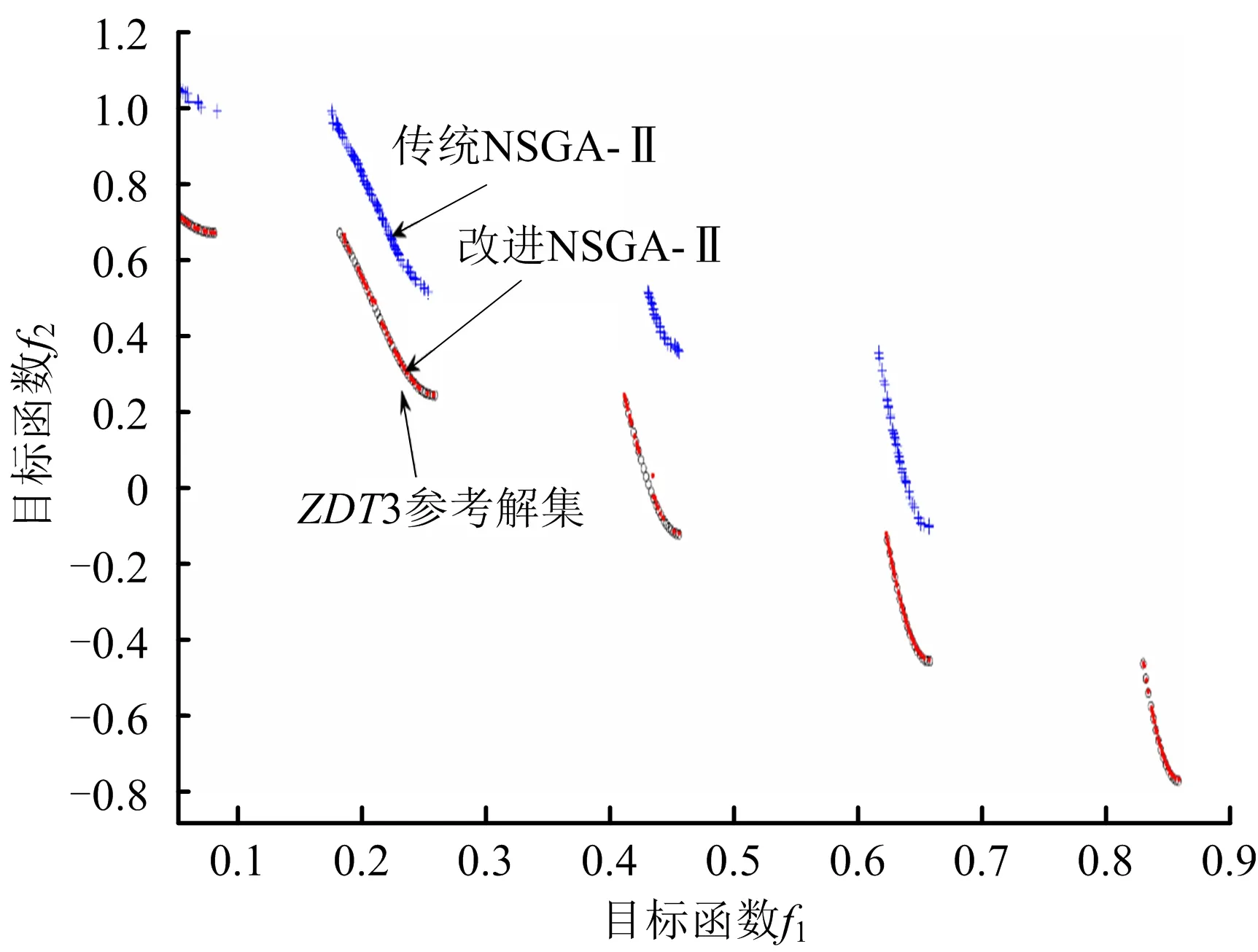
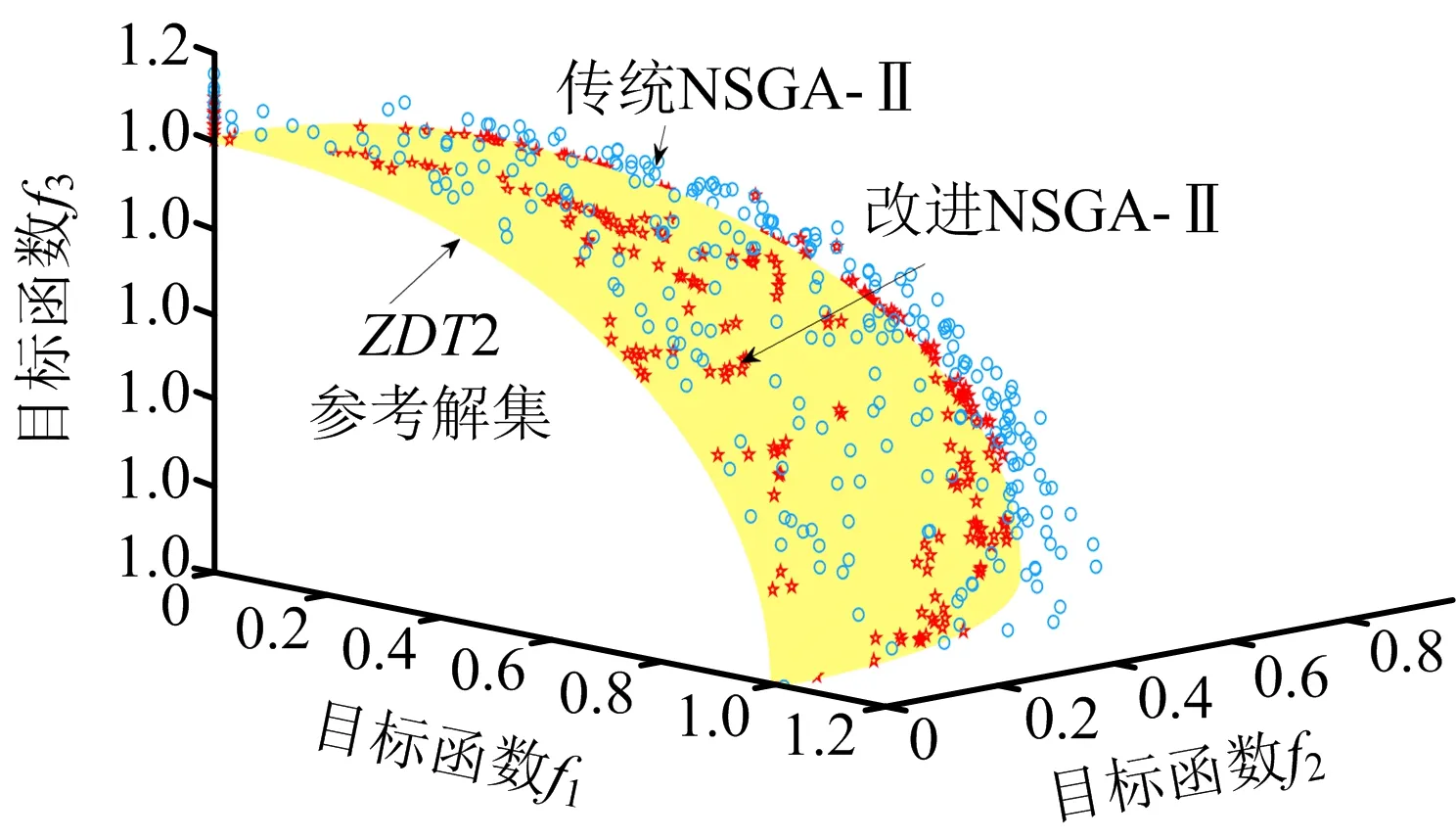
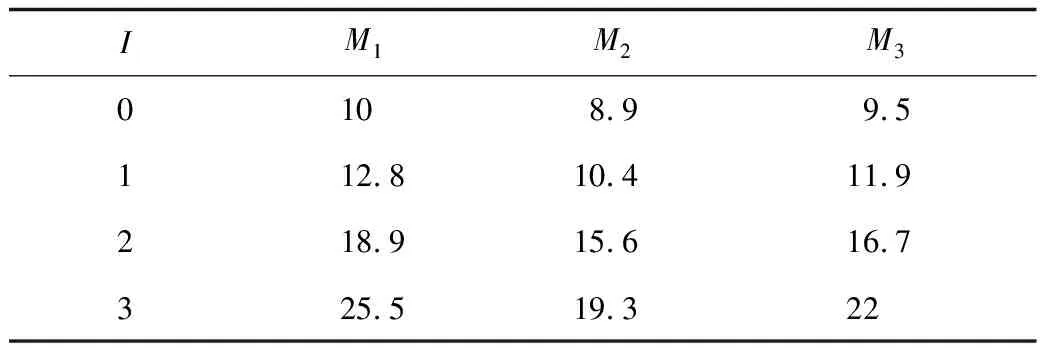
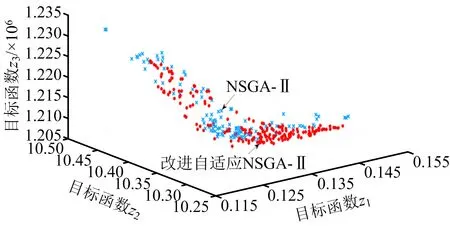
自适应变异算子0 3)自适应精英保留策略改进 将产生的子代种群Gn按式(15)随机挑选出新子代精英种群NGn,同时为防止父代精英个体基因遗失,选择父代种群En中Pareto等级低、拥挤度大的个体合并生成新种群Ln,直到Ln的规模达到N为止。该方法与传统的父、子代种群合并生成新种群相比,前期精英规模较小,可以丰富种群的多样性;后期随精英规模增加,不断提高种群的收敛性,可避免产生极端解,实现全局最优,如式(15)所示: (15) 式中:an为第n代精英保留规模的影响因子。 应用多目标化算法解决实际问题时,主要从分布性及收敛性2方面进行分析。因此,本文将从基于欧氏距离的收敛性[19]和分布性指标[20]进行评估。 1)世代距离的收敛性指标 收敛指标ca可以评估算法理想的Pareto最优前沿程度,定义如式(16)所示: (16) 式中:Nd为算法求出的非支配向量个数;di为算法已知个体边界与真正Pareto的欧几里得距离。 2)空间评价的分布性指标 指标sa用于评价多目标优化算法所求的解集的分布性,如式(17)所示: (17) 本文通过标准测试函数ZDT3和DTLZ2对该模型进行测试与评估,并与传统NSGA-Ⅱ算法对比,2种测试函数最优前沿对比如图3~4所示。 图3 ZDT3测试函数最优前沿比较 由图3可知,改进个体与参考解集基本重合,而传统算法解集个体则与参考值存在偏差。由图4可知,改进算法求得的个体紧密附着于Pareto前沿,而未改进算法求解的个体大多漂浮于Pareto前沿,甚至有少数个体脱离。由此,改进的NSGA-Ⅱ算法更接近最优Pareto前沿,算法精度相对更高。 图4 DTLZ2测试函数最优前沿比较 假设我国某地区发生突发灾难事件,应急管理部门需要制定应急预案,并根据实际情况及时对应急方案进行调整。根据该地区目前灾情和以往发生灾害情况,该地区有2个需求地D1,D2,需要应急生产和运输某应急物资共35 000件;由2个供应商S1,S2提供原材料,1 kg原材料可生产1件应急物资,其中S1最多可供应19 000 kg,S2最多可供应17 000 kg;3个制造商M1,M2,M3负责应急物资的生产和运输。本文运用DTMC-MOP模型模拟应急生产与调度情况,制定最佳应急方案。该模型具体参数设置如下: 应急供应链初始状态概率分布P0及状态转移概率矩阵Pij如式(18)所示: (18) 本文运用MATLAB R2020b软件编程求解模型。首先依据式(4)、初始概率分布P0和状态转移概率矩阵Pij经过200次迭代实现应急供应链状态的动态转移,求得唯一平稳概率分布π=(0.461 0 0.294 8 0.169 8 0.074 4),将表1~5的参数依据平稳概率分布进行加权处理,并输入如下参数:Cs1=6.3,Cs2=6.5,元;Cm1=18,Cm2=19.5,Cm3=19,元;k1=89,k2=92,k3=90,%;Q1=20 000,Q2=15 000,件。其次,对于改进的NSGA-Ⅱ算法基础参数设置如下:种群规模N=200,自适应交叉概率Pc在0.2~0.8之间,变异概率Pm在0~0.1之间,最大迭代次数MG=200,运行2种算法程序得到Pareto最优前沿,如图5所示。 表参数设置 表参数设置 目标函数Z1供应物资需求未满足率大小、Z2供应时间长短以及Z3供应成本高低3者之间的关系。由图5可知,最优解在三维空间中形成1个分布均匀的曲面,能够较好地收敛于Pareto最优前沿,改进自适应NSGA-Ⅱ算法曲线分布在传统算法曲线下方,获得更贴近理想值的Pareto前沿,目标结果更优。 表参数设置 表参数设置 表5 ti参数设置 图5 Pareto最优前沿 从改进自适应NSGA-Ⅱ算法的Pareto最优前沿中分别选取单个目标函数值最小的3组具有代表性的解,见表6。根据决策者的偏好差异可以选择不同的解决方案,若决策者倾向于物资未满足率最低,最佳方案是方案1;若决策者追求物资供应时间最短,应该选择方案2;若决策者希望实现最低的物资供应成本,方案3是最好的选择;若决策者想综合考虑3方面的因素,可以在其他Pareto最优前沿中选择相适应的应急方案。 表6 Pareto典型解 1)提出DTMC-MOP模型,制定有效的应急物资生产与调度方案。基于DTMC模型中的状态转移概率矩阵刻画应急供应链的动态性特征,可用于识别、分析、应对应急供应链风险。在此基础上结合MOP模型,构建供应物资满足率最大、供应时间最短、供应成本最低的DTMC-MOP模型,运用该模型可以很好地解决因风险扰动引起的生产、运输能力变化,得到3个目标的总体最优策略。 2)采用改进自适应的NSGA-Ⅱ算法求解模型,优化算法的收敛性和分布性,得到精度更高、更加贴近理想Pareto最优前沿的结果。通过改进初始化种群、自适应交叉和变异算子、自适应精英保留策略,提高算法的全局、局部搜索能力,决策者可以依据应急管理核心目标或是不同的偏好选择相适应的应急方案。2.2 模型评价指标
2.3 模型测试结果与分析
3 算例分析
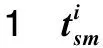

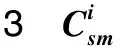
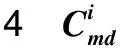

4 结论
