截面形状对旋转扰流柱通道流动换热特性的影响
2022-08-10房兴龙方堪羡李和群
房兴龙,方堪羡,王 澜,李和群
(1.中国航发湖南动力机械研究所,湖南 株洲 412002;2.哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001)
0 引言
涡轮动叶尾缘区域承受着离心力、交变热应力/气动力以及结构强度等的限制,是冷却结构设计时重点关注的区域。目前随着涡轮前入口温度的不断提高,对涡轮动叶区域尾缘的冷却结构设计提出了新的挑战[1]。因此强化尾缘区域的冷却能力显得尤为重要。
涡轮尾缘区域一般采用扰流柱进行冷却,扰流柱通过增加流体的扰动不断带走壁面附近的热量达到冷却叶片表面的目的[2]。目前国内外对于扰流柱的研究主要集中在静止状态,研究结果表明扰流柱几何参数对换热和流动阻力有着显著影响。这些几何参数包含扰流柱的高径比[3]、间距[4]、排布方式[5]以及扰流柱的截面形状等[6-7]。和其他几何参数相比,扰流柱的形状对换热的影响更大[13-18]。扰流柱的不同形状通过影响马蹄涡/尾迹的产生和发展过程改变流动换热特性。
近些年一些学者开始研究旋转扰流柱通道中的流动换热特性,研究表明旋转通道中的流动换热特性和静止通道有显著区别[19-20]。在旋转通道中,科里奥利力和浮升力改变了马蹄涡/尾迹的发展过程。然而上述研究主要是揭示旋转作用的影响,尚未有人研究不同扰流柱参数在旋转作用下对流动换热特性的影响。
基于此,本文拟采用数值研究方法,探究不同扰流柱形状在旋转条件下的流动换热特性,获取通道内部的流阻和换热系数分布,得到旋转作用下较佳的扰流柱形状,为后期的涡轮动叶尾缘设计提供参考。
1 数值计算
1.1 计算模型和边界条件
本次计算的几何模型参考文献[21],为了减少计算量,仅选择一个通道进行计算,几何参数模型如图1所示。通道高度H/D=3,扰流柱的横向间距为S1=2.5D,纵向间距为S2=5.0D,扰流柱通道的旋转半径为R=81.9D。
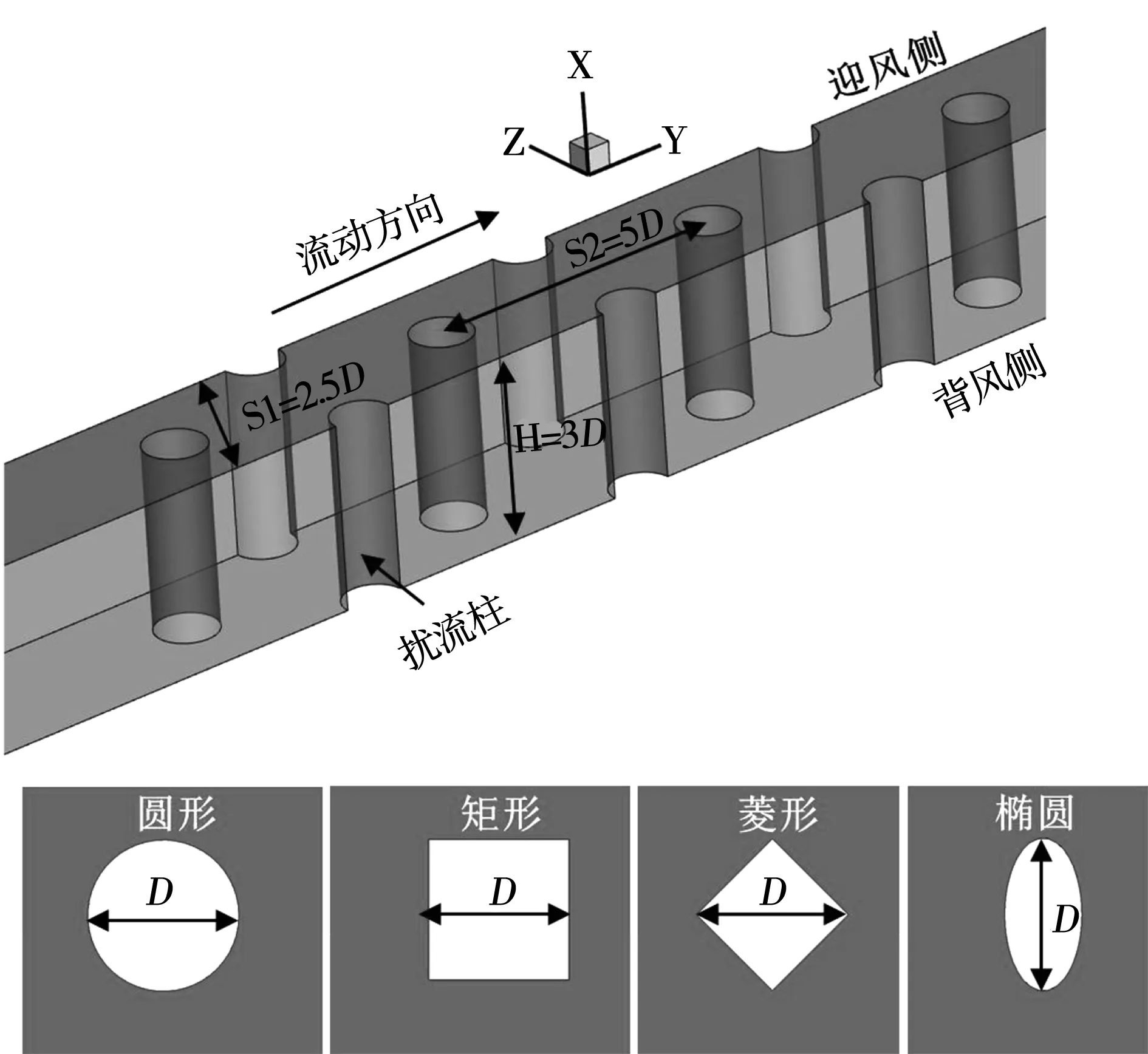
图1 扰流柱通道模型示意图
1.2 参数定义
雷诺数(Re)的定义为
(1)
式中ρ——通道入口处的密度/kg·m-2;
U——通道入口处的平均速度/m·s-1;
DH——通道入口处的当量直径/m;
μ——通道入口处的动力黏度/Pa·s。
通道的旋转数(Ro)的定义为
(2)
式中ω——通道旋转角速度/rad·s-1。
通道中的换热系数(h)定义为
(3)
式中q——热流密度/W·m-2;
Tw——壁面温度/K;
Tb——气体平均温度/K。
通道中的努塞尔数(Nu)定义为
(4)
式中λ——热流密度/W·(m·K)-1。
1.3 数值验证
数值计算过程中湍流模型的选取至关重要,本文研究的工作条件包含静止状态和旋转数状态。因此湍流模型必须能够同时准确预测这两种工作条件下的流动换热特性。静止状态下的数值验证采用文献[22]的实验数据。图 2(a)展示了不同湍流模型时努塞尔数和实验数据对比。可以看出在静止条件下Realizablek-ε湍流模型拥有较好的精度,此外国内相关研究也表明静止扰流柱通道的数值计算中,Realizablek-ε拥有较高的精度。基于Park等人[21]的实验数据用来选择合适的湍流模型预测旋转状态下流动换热特性。图 2(b)展示了迎风面的努塞尔数分布。可以看出在扰流柱的后方有一个低换热区域,各种湍流模型均捕捉到了该特征。在扰流柱前缘出现了高换热系数区域,k-ω和SSTk-ω湍流模型的预测值低于实验结果,但是Realizablek-ε湍流模型的预测数值和实验接近。图 2(c)展示了背风侧的努塞尔数分布,背风侧的换热系数低于迎风侧,各种湍流模型均捕捉到了该趋势,但是Realizablek-ε湍流模型结果和实验值更加吻合。基于上述数值验证的结果,本文采用Realizablek-ε湍流模型进行后续的数值研究工作。

图2 扰流柱通道数值和实验结果对比
1.4 边界条件
本文边界条件参考文献[21]的实验工况。入口雷诺数Re=7 000,湍流度5%,入口空气温度为300 K,端壁和扰流柱表面给定恒定热流q=1 000 W·m2,出口给定一个大气压。
计算域的离散采用多面体网格,如图3所示。多面体网格具有质量高、网格节点少、精度高和收敛速度快等优势,近些年开始广泛的使用在航空发动机涡轮传热领域的研究工作[23-24]。

图3 扰流柱通道多面体网格划分示意图
为了保证传热计算的准确性,壁面第一层网格高度为 0.01 mm,y+<1,壁面棱柱层网格为15层,增长比为1.2。根据网格无关性的验证,最终多面体网格数量为150万。
2 结果分析
2.1 一维结果分析
图4是不同扰流柱截面形状和旋转数条件下的壁面平均努塞尔数分布。在静止条件下圆形扰流柱的换热能力最低,椭圆形和菱形的换热能力最强。该结论和之前国内外的研究结论保持一致。在旋转状态下,换热能力产生了较大的变化。在迎风面随着旋转数的增加,不同形状扰流柱的努塞尔数均有提高,但是提高的速度不一,矩形通道的努塞尔数对旋转数的改变并不敏感。当旋转数大于0.4之后,矩形扰流柱的换热能力最差。此外随着旋转数的增加,菱形和椭圆形扰流柱通道的努塞尔数逐渐趋于一致。图4还显示出背风侧的努塞尔数和迎风侧有较大差距。在旋转数为0.2时,背风侧所有扰流柱通道的努塞尔数均比静止状态小。当旋转数大于0.2之后,努塞尔数均随旋转数的增加而增加。此外随着旋转数的增加,扰流柱形状对换热的影响逐渐减小。对比迎风面和背风面的努塞尔数可以看出,菱形和椭圆形扰流柱通道的迎风面努塞尔数高于背风面,矩形扰流柱通道的背风面换热系数高于迎风面。圆形通道在低旋转数时迎风面的努塞尔数高于背风面,然而在高旋转数时迎风面努塞尔数低于背风面。

图4 旋转数和努塞尔数之间的关系
对冷却结构设计而言,阻力损失也是核心指标之一。对于静止通道一般采用阻力系数进行衡量,旋转通道中有外界做功,采用阻力系数衡量不合理。本文采用壁面剪切应力衡量通道内部的阻力损失。图5展示了迎风面和背风面的壁面剪切应力分布。在静止状态,矩形通道的壁面剪切应力最低,菱形通道的剪切应力最高。旋转状态下,迎风面的剪切应力随着旋转数的增加而不断增加,不同扰流柱截面形状的增加幅度类似;背风侧的壁面剪切应力随着旋转数的增加而降低,但是随着旋转数的增加扰流柱形状的影响逐渐减小。
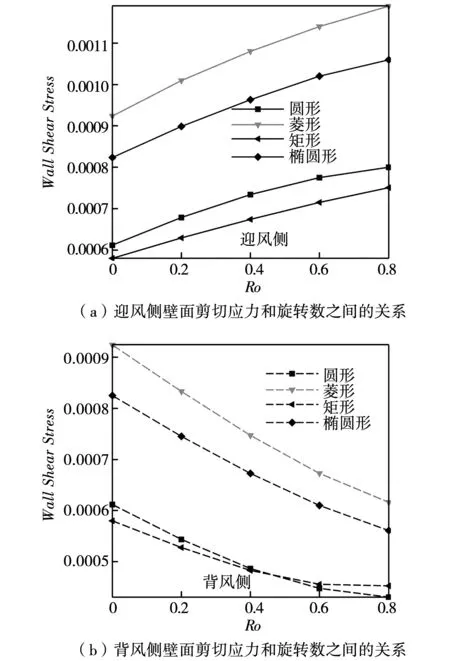
图5 旋转数和壁面剪切应力之间的关系
2.2 努塞尔数分布特性
图6展示了不同截面形状和旋转数条件下扰流柱通道表面努塞尔数分布。可以看出扰流柱通道内部换热增强得益于前缘马蹄涡的生成。圆形扰流柱前缘马蹄涡对应的高换热区域面积较小,因此圆形扰流柱通道的换热能力较弱;椭圆形扰流柱前缘马蹄涡对应的高换热区域面积最大,因此总体换热性能最强。此外不同扰流柱形状也导致了不同的尾迹区域,尾迹区域的换热一般较小。

图6 不同截面形状时扰流柱通道Nu数分布
与静止状态时努塞尔数分布相比,旋转状态下的努塞尔数分布产生了较大变化。随着科里奥利力的增强,扰流柱通道背风面尾迹区域后方出现了长条形的高换热区域。其中圆形和矩形扰流柱通道的该高换热区域面积较小,因此壁面平均努塞尔数较小,如图4所示。随着旋转数的增加,背风面尾迹区域对应的低努塞尔区域逐渐增加,但是迎风侧尾迹区域对应的低努塞尔区域逐渐减小。
图7显示了展向平均努塞尔数沿着流动方向的分布。图7(a)可以看出在背风面扰流柱形状对努塞尔数的影响大于旋转数的影响。矩形和椭圆形扰流柱通道在前缘附近换热能力均优于其余两种形状。菱形扰流柱的前缘努塞尔数最低,这和前缘附近马蹄涡较弱有较大关系,然而菱形扰流柱尾缘附近的努塞尔数较高,在尾迹区域圆形和矩形扰流柱的努塞尔数最低。图7(b)展示了迎风面的努塞尔数分布。可以看出旋转数和形状均对努塞尔数带来了较大的影响。从旋转数角度而言,旋转数越高迎风面的换热能力越强,尤其是尾迹区域的换热能力的增加幅度较高。菱形扰流柱尾迹区域努塞尔数的增长最迅速,矩形扰流柱通道的增长相对缓慢。椭圆形扰流柱前缘附近的换热能力最强,圆形扰流柱前缘附近换热最弱。扰流柱形状还影响了前缘到尾缘的努塞尔数下降速率,菱形扰流柱通道的努塞尔数下降趋势最缓慢,换热分布更加均匀。

图7 展向平均努塞尔数沿流动方向分布
2.4 流场分布特性
图8展示了不同旋转数和不同扰流柱形状时中间截面的流线和速度分布。在旋转作用诱导出的科里奥利力作用下,主流区域的流体从背风面推向迎风面,导致迎风面附近的速度较高。随着旋转数的不断增加,迎风面的速度也在不断增加。此外在旋转作用下,尾迹区域出现了从迎风面指向背风面的纵向二次流,该纵向二次流的存在已经在相关文献中证明。该二次流削弱了背风面扰流柱后方壁面边界层厚度,导致了背风面尾迹后方狭长的高换热区域。随着纵向二次流的增强,背风面尾迹区域高换热系数的区域不断增加。图8还表明扰流柱的形状对流场有较大的影响。首先影响的是扰流柱尾迹区域的范围,菱形扰流柱尾迹区域最长,矩形扰流柱尾迹区域最短。尾迹区域较短,则尾迹区域不易受旋转作用的影响,反之亦然。扰流柱形状还改变了前缘附近的速度分布。矩形通道较大的尾迹区域挤占了主流的通流面积,因此流速较快。

图8 中间截面流场分布和速度分布
为了进一步展示旋转效应和扰流柱形状对流场的影响,图9展示了背风面壁面极限流线和壁面剪切应力分布。从图9可以清晰的看到不同形状扰流柱尾迹区域的形状有显著差异。在静止状态下圆形和矩形扰流柱的尾迹区域形态较为相似,以一对螺旋点为主要特征。菱形和椭圆形扰流柱的尾迹区域显著长于其他两种扰流柱诱导出的尾迹区域。随着扰流柱从静止状态转向旋转状态,扰流柱尾缘区域形态有了较大的变化。在纵向二次流的影响下,背风面尾迹区域的螺旋点逐渐消失,意味着尾迹区域不断被破坏。同时由于旋转数不断增加,纵向二次流的影响范围逐渐扩大,扰流柱后方低壁面剪切应力区域的面积不断扩大。然而不同扰流柱形状尾迹区域的变化呈现出一定的差异。当Ro=0.4的时候,矩形通道的尾迹区域的螺旋点依然存在,这也结解释了矩形扰流柱背风面努塞尔数对旋转数的变化不敏感。菱形扰流柱尾迹区域的螺旋点已经完全消失,对应着菱形扰流柱背风面换热系数对旋转数的变化较为敏感。除了尾迹区域,前缘马蹄涡也有较大改变。一般而言,前缘马蹄涡附近的壁面剪切应力随旋转数的增加而增加,圆形扰流柱对应的剪切应力偏小,椭圆形扰流柱对应的剪切应力偏大。

图9 背风面壁面极限流线和壁面剪切应力分布
图10展示了迎风面的壁面极限流线和剪切应力分布。和背风面相比,旋转作用对迎风面的作用效果较弱。主要因为纵向二次流在输运过程中不断减弱和耗散,到达迎风面时的动量较小,不足以对迎风面的流动产生较大的影响。然而科里奥利力指向迎风面,导致迎风面主流区域的壁面剪切应力随旋转数不断增加。此外形状对迎风面的影响和静止状态基本一致。扰流柱的形状主要影响了迎风面尾迹区域的长度和宽度。

图10 迎风面壁面极限流线和壁面剪切应力分布
3 结论
本文采用数值模拟方法,以涡轮动叶尾缘扰流柱通道为研究对象,分析了不同旋转数和扰流柱形状对换热和流动的影响规律,探究了努塞尔数、壁面极限流线以及剪切应力的分布,主要结论如下:
(1)扰流柱的形状显著改变了马蹄涡和尾迹的特征,进而改变了通道内部的流场和换热特性。椭圆形和菱形扰流柱的换热能力最强,矩形和圆形扰流柱通道的换热较弱。
(2)旋转扰流柱通道的尾迹区域出现了迎风面至背风面的纵向二次流,该二次流显著改变了背风面尾迹区域的流动形态和换热分布,诱导出了狭长高换热区域。
