自动机曲线导轨动载冲击研究
2022-08-10赵建中刘建斌任弘毅
豆 征,赵建中,刘建斌,任弘毅
(西北机电工程研究所, 陕西 咸阳 712000)
1 引言
自动机是中小口径常规武器的核心构成,导轨是自动机遂行一系列功能的重要依托。导轨的精度、可靠性是自动机整体寿命的关键体现,研究导轨受冲击情况,改善其导引特性,对于延长自动机使用寿命具有重要意义。
文献[1-2]研究了冲击作用下的结构性能;文献[3-8]研究了直线导轨的静态性能、动态特性、接触力学状态等;文献[9-12]研究了曲线导轨输出特性、疲劳寿命、试验状况等;文献[13]分析了自动机导轨的动力学特性,结合约束条件和内弹道安全,建立了优化的轮廓方程,利用多刚体动力学理论,对比优化前后的动力学性能;降低了自动机驱动功耗;文献[14-15]研究了曲线导轨的设计;文献[16]根据试验中自动机导轨发生卡滞和磨损情况,研究了闩体滚轮和导轨正压力问题,依据达朗贝尔原理,得到星形体运动平衡方程,分析了正压力与导轨倾角的关系;文献[17]基于内弹道理论和气体动力学理论,采用旋转活塞驱动转管武器,建立了相关数值模型;文献[18-19]研究了曲线导轨传动过程中的碰撞和传动问题;文献[20-21]研究了直线导轨精度与结构的关系;文献[22]研究了导轨的阻尼和振动问题。
2 工作原理
星形体与闩体的传动属于空间凸轮机构运动,闩体通过直线滑道安装于星形体内,通过滚轮与镶嵌在炮箱内壁的曲线槽连接。闩体沿曲线槽成空间分布关系,从轴线方向上看,相邻2个闩体的时间相位差为72°。闩体在曲线槽及星形体中的运动属于复合运动,是闩体绕星形体中心线的转动和沿星形体导轨纵向直线运动的叠加,所以可以把星形体的运动分两部分来考虑。自动机工作时,星形体带动5个闩体做旋转运动,同时闩体在导轨约束下做周期性前后运动。星形体组件如图1所示。

图1 星形体组件示意图
3 导轨曲线
自动机曲线导轨数学模型的轮廓曲线生成步骤是:先设计一段曲线,再把设计好的曲线绕制在一定规格的圆柱体表面上;设计曲线是根据导轨遂行的功能、运动特性、各时段分布等由不同的曲线段拼接而成;拼接的约束条件由空间边界、一阶可导、二阶连续等进行权衡优化,既要保证完成功能,又有特定的尺寸条件,尽可能减小硬冲击和柔性冲击。
3.1 坐标体系
导轨曲线如图2,在加速、减速段采用二次抛物线连接。图中:
=×
其中:为曲线的横坐标;为星形体中心到闩体滚轮中心的距离;为星形体的转角;

图2 导轨曲线
根据自动机结构及循环图,可先求出曲线的最高点坐标(,),最前端点(,),(,)及两等速直线段的方程,然后根据已知条件,求出各加速、减速过渡段曲线方程,计算结果见表1。
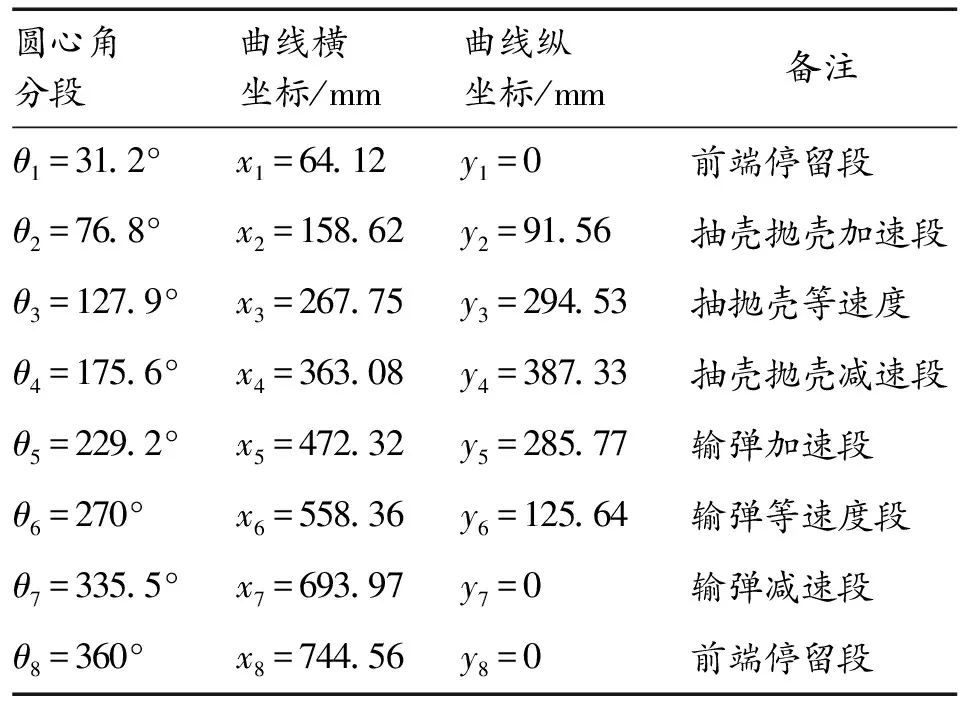
表1 曲线段数据 Table 1 Curve data
3.2 各曲线段方程
抽壳抛壳加速段(≤≤)抛物线过渡段曲线方程为
=(-)(-)
(1)
抽壳抛壳等速段(≤≤)直线方程为
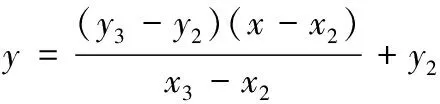
(2)
抽壳抛壳减速段(≤≤)抛物线过渡段曲线方程为
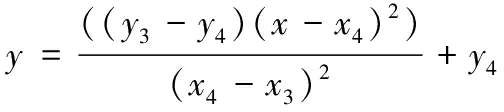
(3)
输弹加速段(≤≤)抛物线过渡段曲线方程为
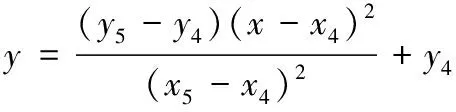
(4)
输弹等速段(≤≤)直线方程为
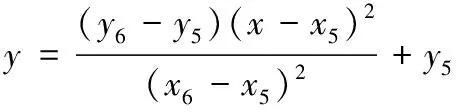
(5)
输弹减速段(≤≤)抛物线过渡段曲线方程为
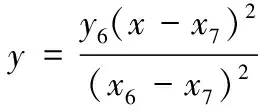
(6)
其中为以闩体闭锁时滚轮的位置为零点,向后为正,闩体滚轮在导轨上的前后位置。
3.3 转动角度
闩体在运动过程中,相对于星形体的姿态的不断变化;考察其转动角度的时变性,利于分析闩体动载变动情况。
如图3所示,附着于星形体中心的坐标系为,附着于闩体的坐标系为′′′,在坐标系中假设有一点,点坐标为(、、),然后围绕轴旋转角,得到′′′。
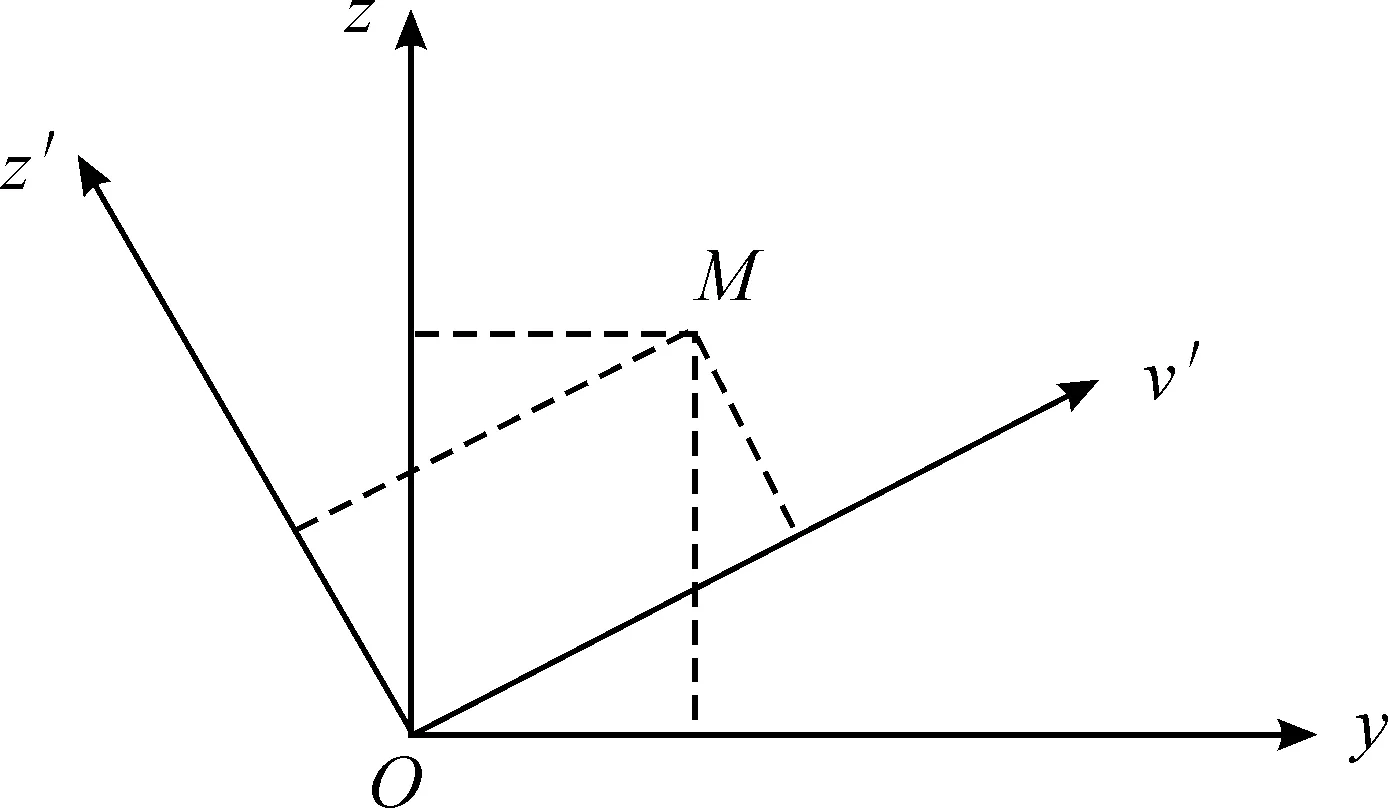
图3 对应点坐标关系图
2种坐标系的对应点坐标关系如下:
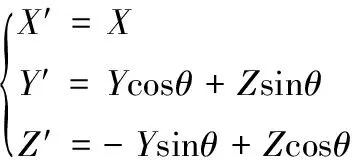
矩阵形式
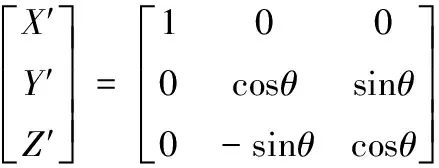
分别绕轴旋转角,绕轴旋转角,得到

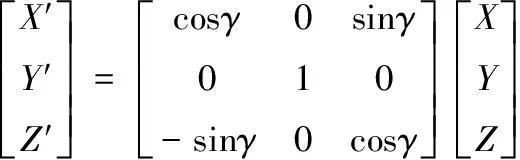
其姿态矩阵为

其中,
=sincos+cossinsin
=sinsin-cossincos
=coscos
根据姿态矩阵可以求解出闩体任一位置相对星形体的坐标关系,从而分析其动力学特性及位移、速度、加速度变化情况。
3.4 曲线引入
设引入的3次样条曲线为
=+++
根据连续性条件,在不同曲线的连接点,dd、(dd)d连续,这一连续性条件,保证了位移、速度、加速度的连续,降低了动载冲击。
4 动载冲击对导轨的影响
4.1 闩体的速度及加速度变化
闩体一方面可以在星形体的滑槽上反复滑动,由于星形体转动而获得动能,一方面在导轨上周而复始的运动,完成输弹、关闩、闭锁、抽壳一系列动作,闩体在一个运动周期内(几十毫秒),速度、加速度急剧变化,速度的剧变意味着导轨承受着局部弹塑变及摩擦力,加速度剧变对导轨形成柔性冲击,引发疲劳破坏。
星形体转动为闩体提供运动能量,由于星形体本身转动惯量很大,转动角速度及角加速度幅值高,角加速度变化剧烈,其巨大的周向冲击(包括硬性冲击和柔性冲击)最终通过闩体传导给导轨,造成导轨局部反复弹塑变,引发疲劳破坏、精度下降、可靠性降低。
参考一般工况,在自动机转速4 000(°)/s,角加速度1 200(°)/s的情况下对闩体与星形体组件进行运动仿真。
在三维设计软件UG中建模,为防止导入其他动力学分析软件数据格式交换可能引起的畸变,直接启用UG动力学分析模块。各运动副中不设置摩擦和阻尼,不考虑装配误差及动态形变,各构件视为刚体。
仿真条件:采用右手坐标系,射击方向与轴方向同向,仿真时长1 s,步长2 000步。
如图4、图5所示,闩体相对星形体的姿态角、反复急剧变化,1~2 ms内90%以上的变动幅度(0.46 s时,角位移从154°降至7°用时0.05 s;0.6 s时,角位移从178°降至-162°用时0.02 s),20 Hz以上的变动频率,而姿态角的每一次变化意味着能量的传导过程在1~2 ms内完成,这样的能量传导过程每秒高达20次以上;如果没有柔性冲击,闩体与导轨之间只有摩擦磨损,柔性冲击的存在,使得每一次冲击能量被相应位置的闩体和导轨接触处吸收,变成弹性能与塑变能,同时还伴随着摩擦磨损,反复的弹塑变会导致疲劳破坏,精度下降。
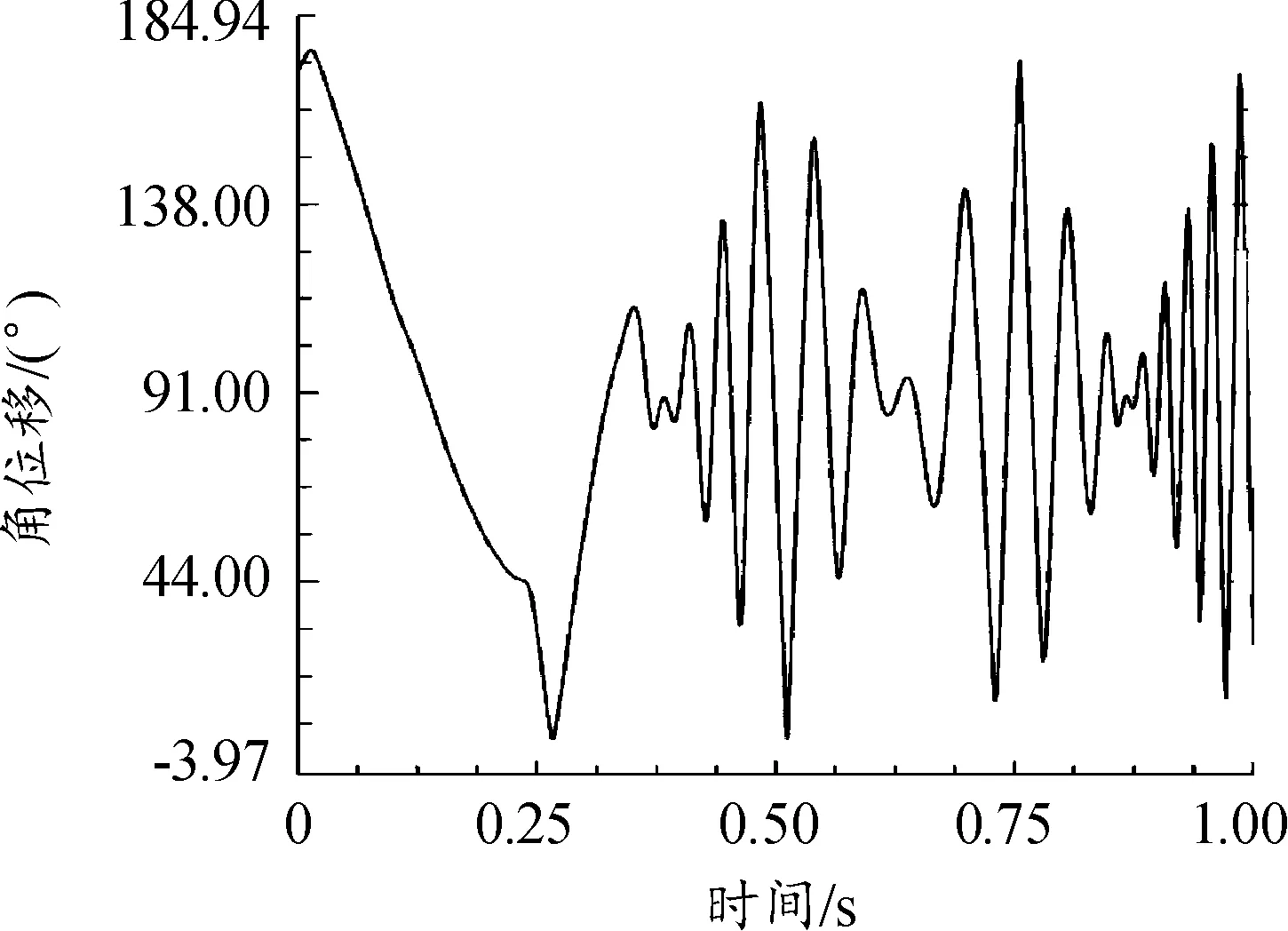
图4 闩体相对星形体的姿态角ψ角位移曲线
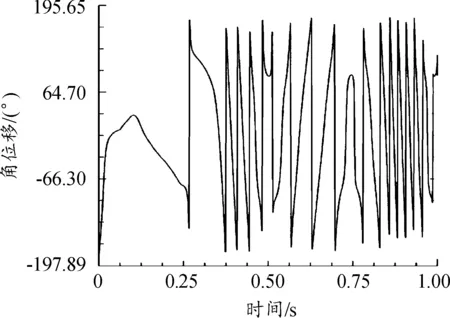
图5 闩体相对星形体的姿态角γ角位移曲线
星形体的角速度与角加速度变化如图6、图7所示。星形体转动惯量大,角速度的急剧变化(0.33 s时,1 950(°)/s升至1 098(°)/s用时0.04 s)使得惯性矩变动幅值巨大,意味着曲线导轨通过闩体对星形体进行频繁“制动”,而每一次“制动”,星形体转动能量大部分被曲线导轨吸收;在图7中,星形体角加速度变动剧烈频繁(0.28 s、0.6 s、0.88 s时),这表明星形体转动的惯性矩动载对导轨的冲击具有较大幅值和较高频度。反复的动载冲击不仅破坏装配可靠性、导转精度、疲劳寿命,还会对弹的运行安全造成隐患。

图6 星形体角速度曲线
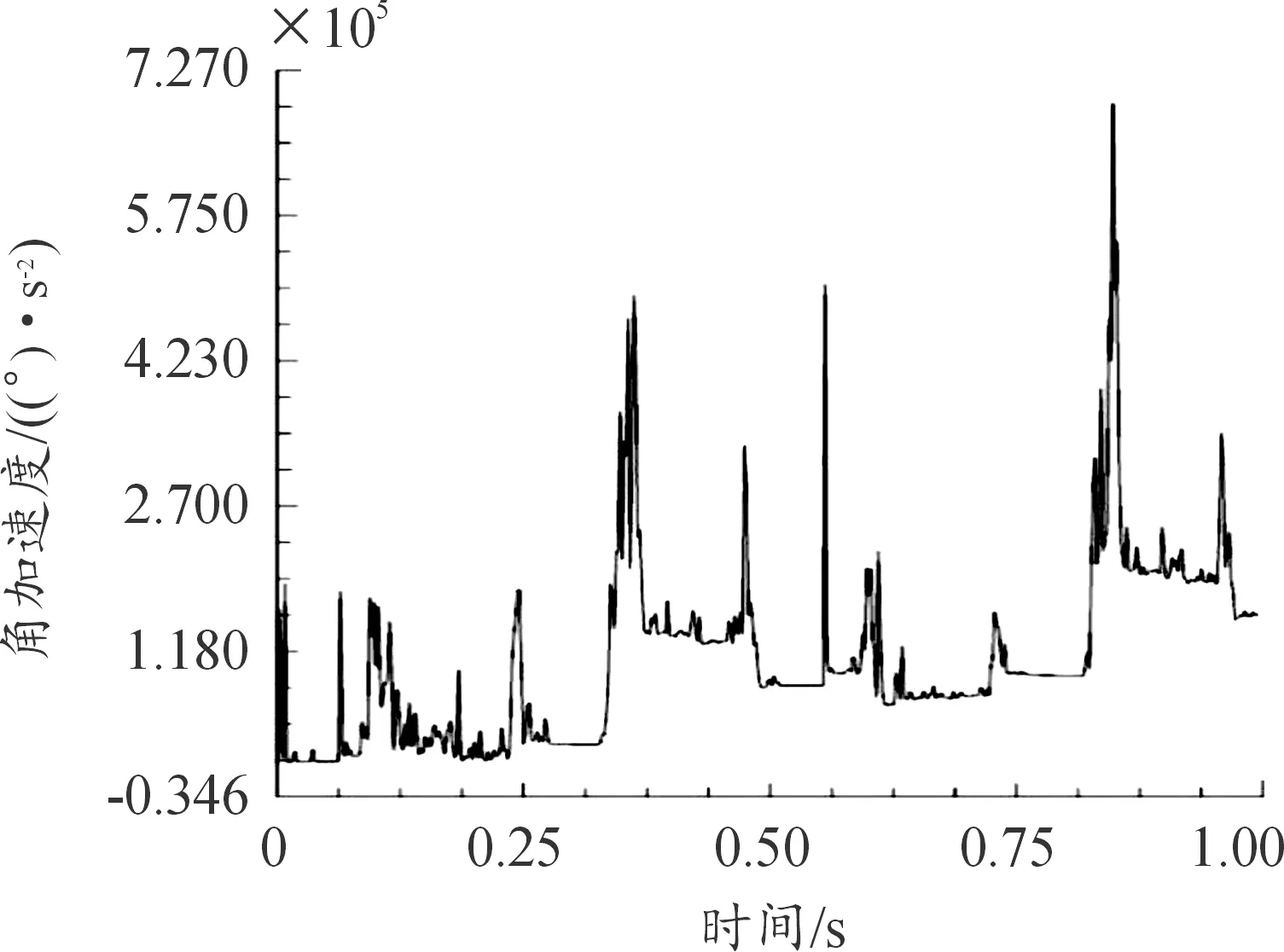
图7 星形体角加速度曲线
闩体在星形体的槽轨中是直线运动,闩体滚轮在曲线导轨中的运动属于空间凸轮运动,这种复合运动由于零部件的破损很容易造成卡滞;由于星形体转动惯量大,角加速度突变幅值大,一旦出现卡滞现象,排除故障非常困难,尤其在实弹运行的情况下。
4.2 闩体与星形体的动载冲击
作用在导轨上的动载有闩体的惯性力和星形体的惯性矩,由于速度突变和加速度突变同时存在,导轨受到的动载冲击既有硬性冲击,亦有柔性冲击,硬性冲击的反复出现易造成导轨局部塑变,柔性冲击的交替发生带来的是局部疲劳破坏。闩体相对导轨曲线运动示意图如图8,闩体动载对导轨的瞬时冲击功微分方程为
=sin()dd
星形体动载对导轨的冲击功微分方程
=sinsin()dd
其中,d为d微时段内的导轨形变量,d为d微时段内的导轨相对星形体中心夹角的微形变量。
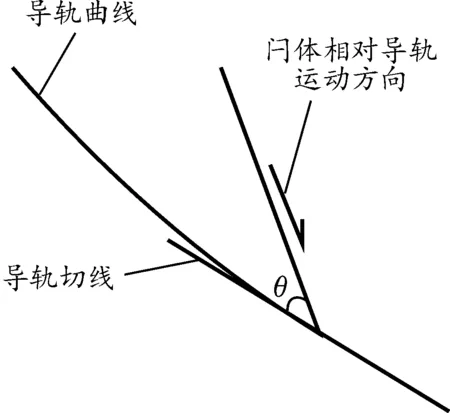
图8 闩体相对导轨曲线运动示意图
4.3 修正设计
通过运动仿真分析,并结合实际情况,较为严重的磨损发生在抽壳抛壳加速段与抽壳抛壳等速段连接处,抽壳抛壳等速段与抽壳抛壳减速段连接处,输弹加速段与等速段连接处,原因是这些节点两边2阶不可导,产生跃度突变(dd),由于自动机射频(发s)反复切换,转速及转动角加速度变化形式多样,克服一系列阻力需要较大的力矩,这就使得跃度幅值较大,对导轨造成较大的反复冲击。
有了曲线的特征点后,可以使用样条插值的方法,拟合出一条在接点处光滑的的曲线。设函数()的自变量区间在[,],=<<…<=,如果函数()通过+1个型值点(,),即()=(=0,1,…,),且在[,]区间上二阶连续,在每一个微小区间(-1,)上均为三次多项式,则函数()为三次样条函数,此函数的几何图形为三次样条曲线。
设和分别表示函数()的一阶和二阶导数,由于函数()在每一个微小区间是三次多项式,所以"()是分段线性函数,于是在(-1,)上,
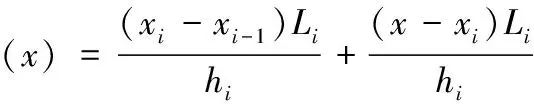
其中,="(),=--1,对"()二次积分,
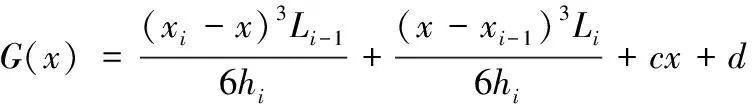
再由(-1)=-1,()=,确定出积分常数、,代入上式并整理:
-1+2++1=(=1,2,…,-1)
其中,=(++1),=1-,
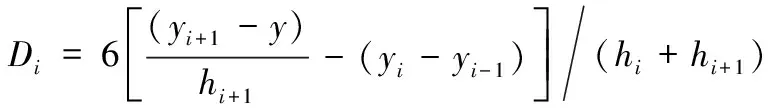
凸轮曲线每一点对应一组数据(,),可以使用3次样条插值法来构造凸轮曲线。3次样条插值曲线,一阶和二阶导数处处连续。这条曲线由通过相邻3个点的3次多项式构成。一系列三次多项式串在一起就组成了完整的3次样条曲线。
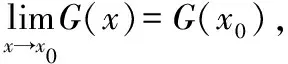
修正前后闩体对导轨的冲击功如图9、图10所示。修正后冲击功峰值降低368,闩体对导轨的冲击工况得到改善。
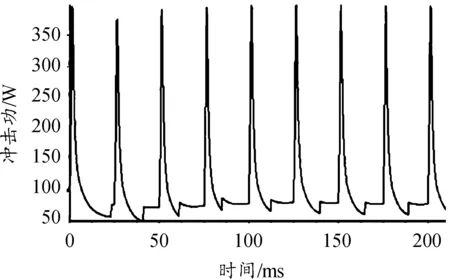
图9 修正前的闩体对导轨冲击功曲线
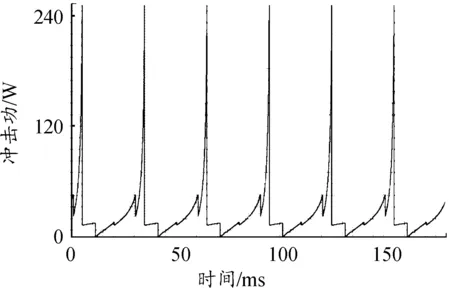
图10 修正后的闩体对导轨冲击功曲线
5 试验
各测点平均声级为,单位为dB;总振级为,单位为dB。
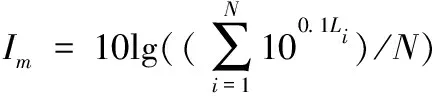
其中,为测点数,为各测点在同一中心频率对应的振级,单位为dB,总振级
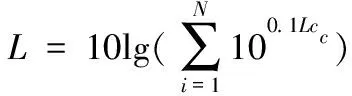
其中,为13倍频程频段数,为倍频程中心频率振级,单位为dB。
在星形体转速为1 200 r/min,闩体携带教练弹的情况下,对2种不同导轨结构的自动机进行噪声测试;测点布置于炮箱周围。
导轨曲线修正以后,由于动载冲击的降低,在同样的星形体转动角速度及角加速度的情况下,幅值下降17%,中心区噪声幅值下降17.5%,测试结果如图11、图12所示。自动机如图13所示。
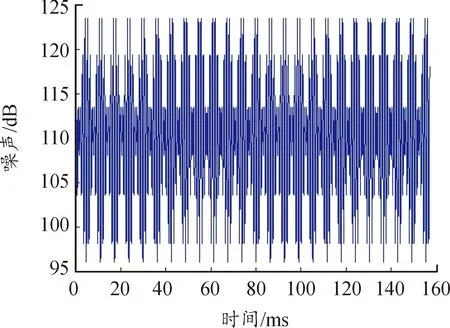
图11 修正前的中心区噪声曲线
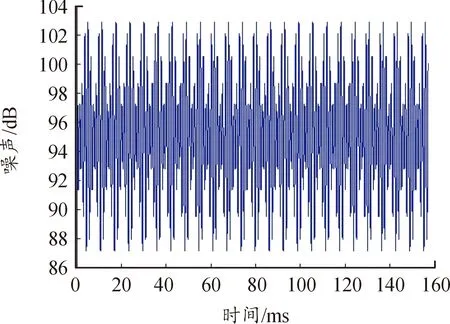
图12 修正后的中心区噪声曲线

图13 自动机示意图
6 结论
1) 导轨曲线段部分连接二阶不连续,由于闩体的加速度突变和星形体的角加速度突变,通过闩体滚轮对曲线导轨造成动载柔性冲击;改进后,动载加速度和冲击功分别减弱23%、36.8%。
2) 通过构建3次样条曲线插值,对导轨曲线连接处二阶不连续的曲线段进行改造,改造后冲击功降低;
3) 通过对2种不同曲线导轨的自动机运行噪声测试,优化后的曲线导轨噪声下降明显。
