基于命中破片数的高炮武器射击控制理论建模与数值预测

王亮宽，吴潇璞，杨卫超，唐 旭，李 鑫

(西北机电工程研究所, 陕西 咸阳 712099)

1 引言

高射速高炮能通过发射预制破片弹来提高对目标的命中概率，受到了世界各国的高度重视。随着军事需求的不断变化，预制破片弹技术仍在高速发展。例如，典型的35 mm多束定向预制破片弹，其主要配用于35 mm高炮武器，通常，高炮炮口装有3个线圈，前2个线圈用来测量弹丸的炮口速度；第3个线圈用来装定弹丸的起爆时刻，以使弹丸在目标前方的某一较佳位置起爆，形成子弹幕以对目标造成高效的命中和毁伤；典型的中口径高炮配用中口径预制破片弹，通过开舱距离的优化，在目标附近形成密集破片提升对导弹的命中概率。

近年来，一些学者在射击弹药数量一定条件下，针对高射速高炮发射多束定向预制破片弹对来袭目标命中及毁伤概率开展了大量的研究工作，也从精确控制发射弹丸数量的角度开展了火炮射击控制模型的相关研究。在命中或毁伤概率研究中,主要的不足是：对射击距离方向上的误差进行了简化处理，命中概率仿真精度不高，难以指导高炮武器的射击控制。关于高炮武器射击控制方法的研究中，没有涉及火炮射击弹药种类带来的射击控制模型的变化；特别是对于高炮武器发射多束定向预制破片弹的射击控制具有一定的随意性、主观性，不利于高炮武器发挥最佳作战效费比。若选择的点射长度较小，点射弹数少，作战费用低，但命中目标破片数少，不能对目标形成有效毁伤；若选择的点射长度大，点射弹数多，命中目标破片数多，可对目标进行有效毁伤，但作战费用高。因此，基于命中破片数，研究高炮武器系统射击控制具有重要意义。

本文从高炮武器的实际射击过程着手，在研究弹丸开舱点三维分布密度函数的基础上，建立了基于命中破片数的高炮武器射击控制模型；进一步地，通过仿真计算了某装备在不同命中破片数条件下不同最远开火距离所需射弹数与点射长度之间的关系。建立的射击控制模型已成功应用于某装备的鉴定试验，效果良好。

2 单发弹丸命中目标破片数建模

如图1所示，建立空间直角坐标系-，-。其中，-坐标系为弹丸开舱点位置的计算坐标系，-为弹丸开舱后的破片命中目标坐标系。点为目标未来点，轴为炮目连线的延长线，正向无穷远。轴与轴位于与垂直的平面上，轴为过铅垂面与垂直平面的交线，轴与轴垂直，正向与航路方向同侧；轴与轴位于过炮目连线的铅垂面上，轴与弹丸速度同向；轴垂直于轴，正向朝上；轴与轴位于与轴垂直的平面上，与重合，方向相反。坐标系-与-各坐标轴夹角的余弦见表1，表中为提前点处的目标高低角，为提前点处的弹道倾角。

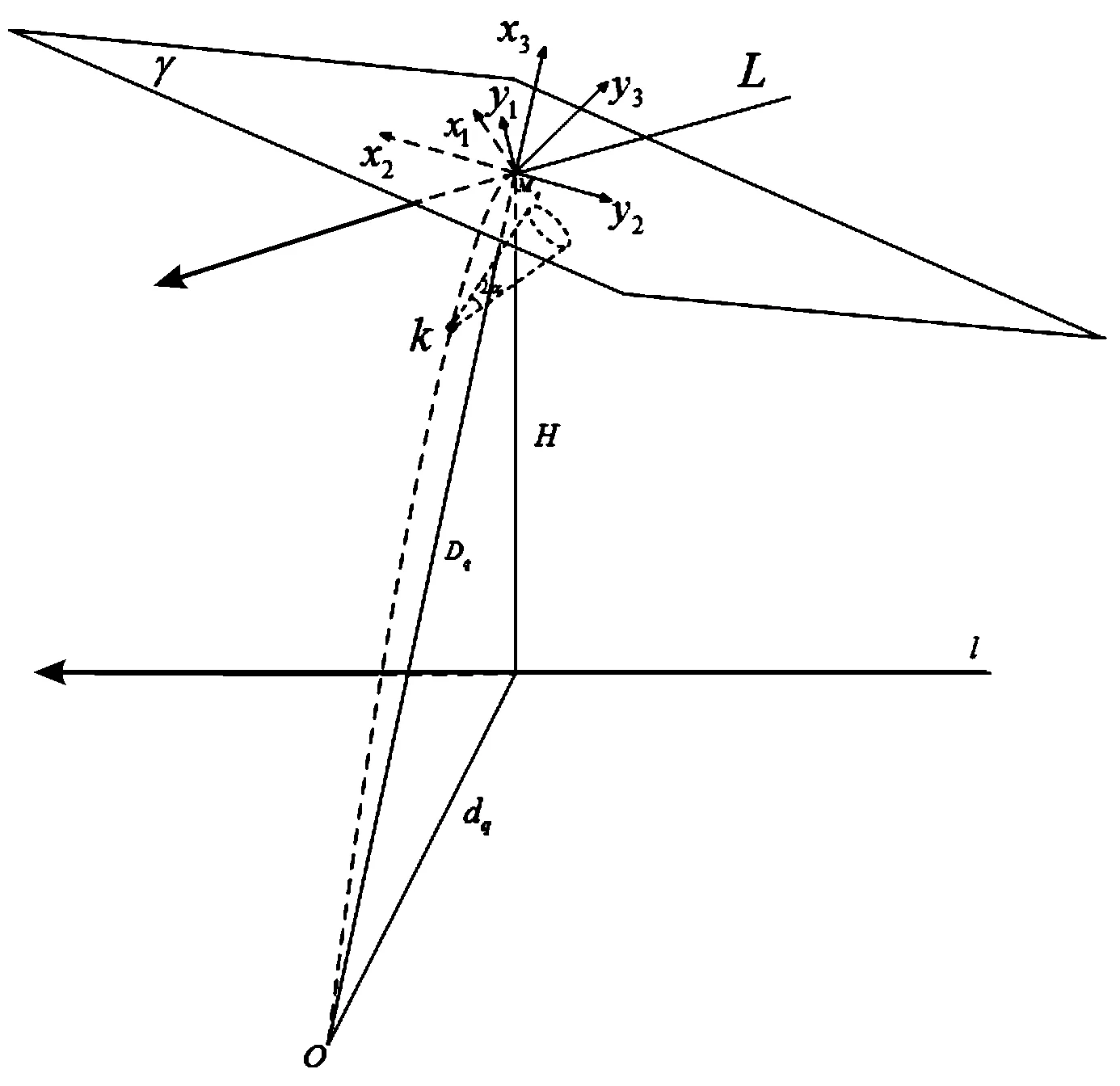
图1 空间直角坐标系示意图

表1 Mq(x1x2x3)与Mq(y1y2y3)坐标轴 夹角的余弦cos(xj,yj)

图1中，为弹丸开舱点。若已知弹丸开舱点在坐标系-中的坐标为[1,2,3]时，在-中的坐标[123]=cos(,)[123]。弹丸开舱后，破片以倒圆锥状向目标飞去，忽略弹丸开舱点与目标点处弹道倾角的变化，且认为弹轴与弹丸速度重合及所有破片近似同时到达拦截平面，则破片在拦截平面上的散布圆半径为：

=3·tg

(1)

式中，为破片飞散半锥角。

假设弹丸抛洒出的破片在拦截平面上是均匀分布的，则在分布圆内的破片密度为：

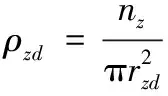
(2)

式中，为单发弹丸抛洒出的破片数。

高炮武器以跟踪射击的方式来拦截目标，每发弹丸对应一个射击诸元。由于探测跟踪误差、火控解算误差、随动误差、火力发射误差、气象条件等因素的影响，每发弹丸的开舱位置是随机的，且服从相互独立的三维正态分布规律。在-坐标系下，开舱点的分布密度函数为：

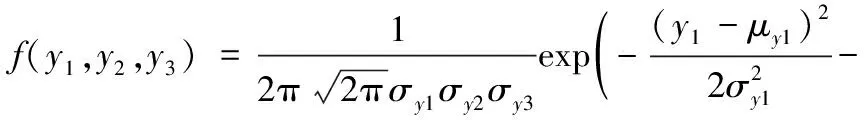
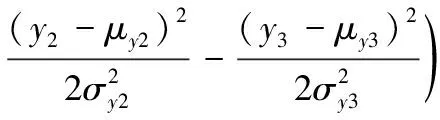
(3)

式中，1、1，2、2，3、3分别为开舱点沿1、2、3三个坐标方向的期望与均方差。

单发弹击中拦截平面上任意一点(1,2)的概率为：

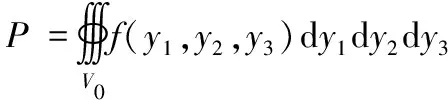
(4)

式中，为开舱点散布椭球体与以子弹散布圆为底的圆柱体相交形成的区域，且满足：

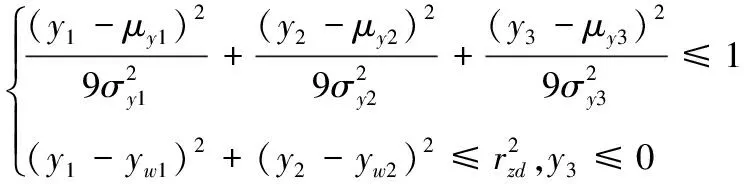
(5)

只有开舱点在区域内时，破片才能覆盖点，则武器系统射击一发多束定向预制破片弹在点处的破片密度函数为：

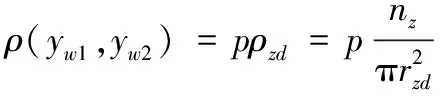
(6)

发射一发多束定向预制破片弹命中目标的破片数为：

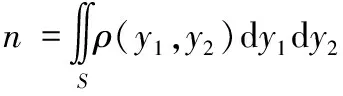
(7)

式中，为目标在拦截平面上的投影面积，可根据目标几何外形与拦截平面法线的夹角确定。

3 基于命中破片数的射击控制模型

高炮武器系统射击过程中，假定期望对某来袭目标的命中破片数量为，统计发射每发多束定向预制破片弹对目标的命中破片数；当统计数量大于所要求的破片数时停止统计，累计的射弹数即为一次射击所需弹丸数；再根据高炮武器的射速，可确定该次射击的点射时间长度。

为了工程应用中的可操作性和有利于保证期望的命中破片数，以最远开火距离点单发弹丸的命中破片数为基础，建立射击控制模型，有

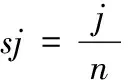
(8)

式中，为所需射击弹药发数。

则点射长度为：

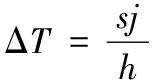
(9)

式中，为高炮武器射速。

4 射击控制模型预测效果

4.1 射击控制参数影响规律

针对S-70靶机目标，编程进行了某型高炮武器系统发射多束定向预制破片弹拦截的射击控制效果预测。单发弹丸命中破片数期望随最远开火点距离的变化如图2所示，预期命中破片数一定条件下所需发射弹数随最远开火点距离的变化如图3所示，预期命中破片数一定条件下点射长度随最远开火点距离的变化如图4所示。

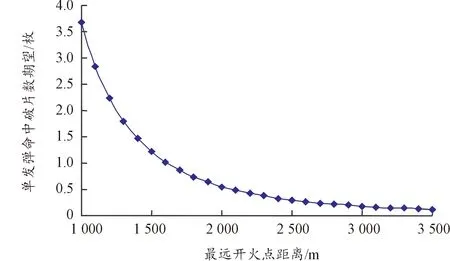
图2 单发弹丸命中破片数与最远开火点 距离关系曲线

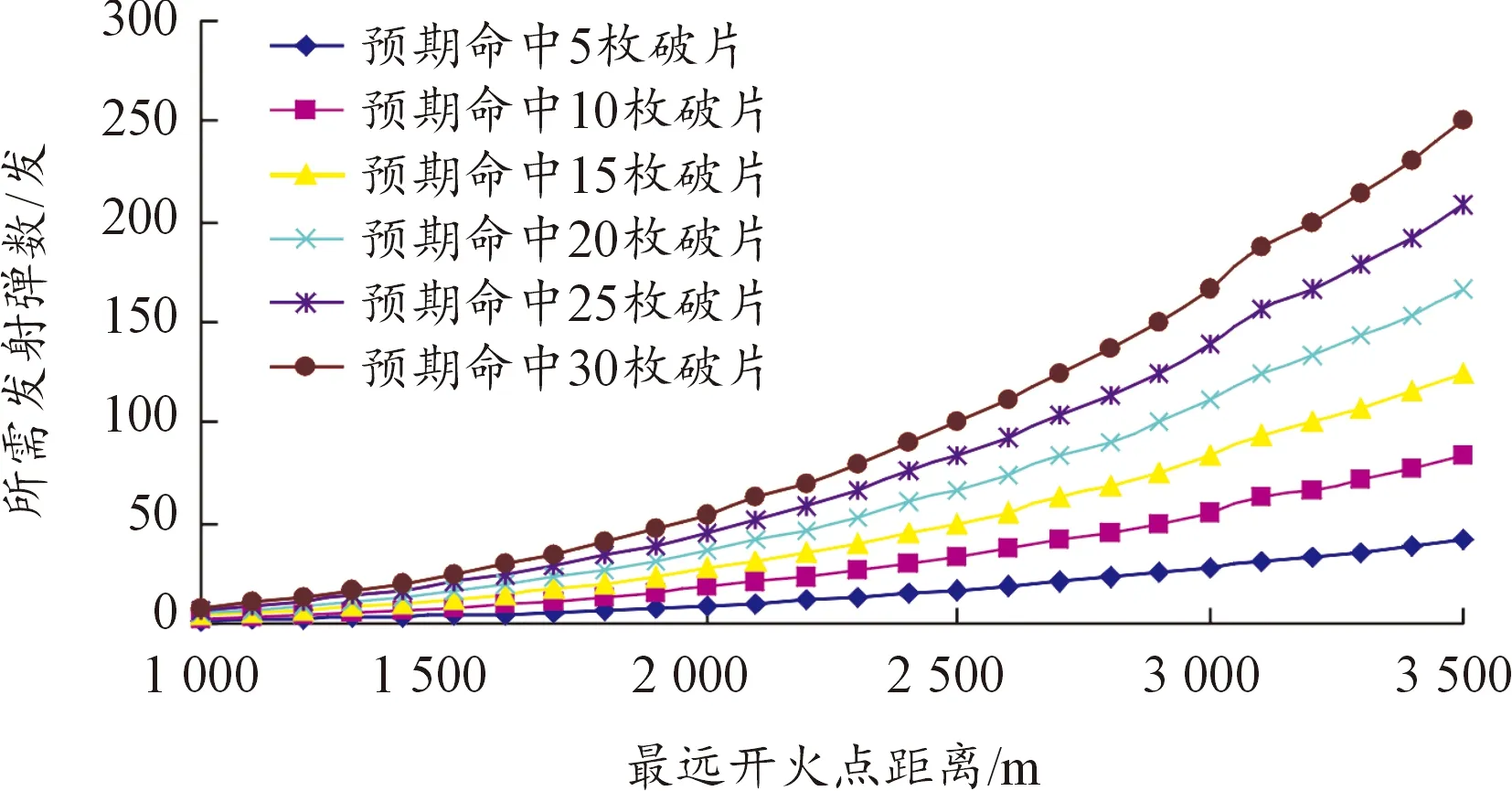
图3 所需发射弹数与最远开火点距离关系曲线

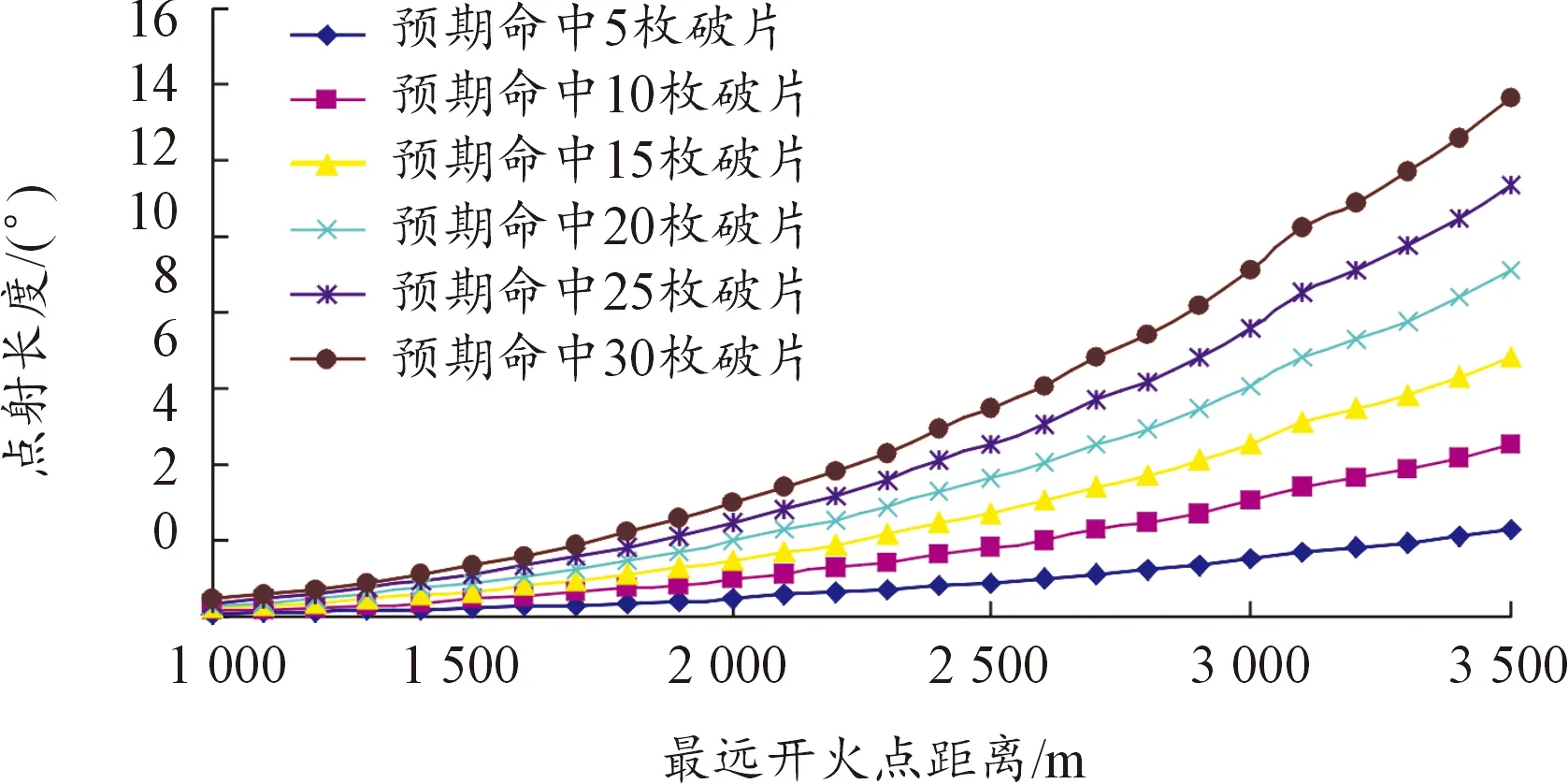
图4 点射长度与最远开火点距离关系曲线

分析图2可知：单发弹丸命中破片数期望随着最远开火点距离的增加而减小；最远开火点距离小于1 500 m时，单发弹丸命中破片数期望减小速率较大；最远开火点距离1 600 m时，单发弹丸命中破片数期望为1.02枚，也即表明最远开火点距离大于1 600 m后，单发弹丸命中破片数期望不到1枚。因此，针对S-70靶机目标，某高炮武器系统最远开火距离不应大于1 600 m。

分析图3可知：预期命中破片数一定，高炮武器系统所需发射的弹药数随最远开火点距离增大而增加；随着预期命中破片数的增大，不同最远开火点距离上高炮武器系统所需发射弹药数增加，且最远开火点距离越远，所需发射弹数增加幅度越明显。

分析图4可知：由于某高炮武器系统射速一定，预期命中破片数一定，高炮武器系统点射长度随最远开火点距离增大而增加；随着预期命中破片数的增大，不同最远开火点距离上高炮武器系统点射长度增加，且射击最远开火点距离越远，点射长度增加幅度越明显。

4.2 射击控制模型应用

某高炮武器系统在某靶场的鉴定试验中，需评估其发射多束定向预制破片弹对S-70靶机的拦截效果。在确定的某高炮武器系统技术状态及靶机飞行航路条件下，要求最远开火点距离为1 500 m。基于上述射击控制模型，在1 500 m最远开火点距离、预期不同命中破片数条件下，某高炮武器系统发射弹数及点射长度预测结果见表2。

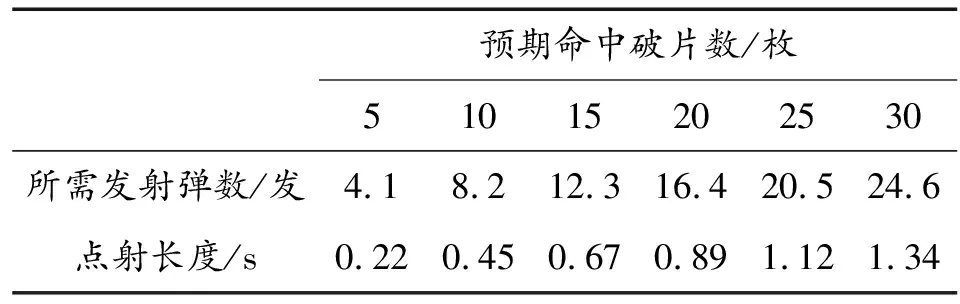
表2 某高炮武器系统发射弹数及点射长度

预期对S-70靶机命中15枚破片即可达到毁伤目的。基于射击控制预测结果，确定某高炮武器系统需射击弹药12发，装定射击点射长度0.67 s，成功将S-70靶机击落(见图5)，回收分析统计命中破片数约为19枚。实际命中破片数大于仿真命中破片数，原因可能是靶机等效投影面积偏小、预测分析按最远开火点距离装定点射长度。

图5 击落的S-70靶机(红圈标注为破片侵彻位置)图

5 结论

针对高炮武器系统发射多束定向预制破片弹精确控制点射长度问题，本文从高炮武器系统实际射击过程着手，制定了基于命中破片数的高炮武器系统射击控制模型，预测了不同命中破片数条件下，不同最远开火点距离某高炮武器系统射击控制方法，得到结论如下：

1)在研究弹丸开舱点三维分布密度函数的基础上，建立的高炮武器系统命中目标破片数模型能够反应高炮武器实际射击全过程、射击控制模型能够很好指导高炮武器对空射击控制。

2) 预测结果表明，命中破片数期望随着最远开火点距离的增加而减小；最远开火点距离小于1 500 m时，命中破片数期望减小速率较大；预期命中破片数一定时，所需发射的弹药数及点射长度随最远开火点距离的增大而增加；随着预期命中破片数的增大，不同最远开火点距离上所需发射弹药数及点射长度增加，且最远开火点距离越远增加幅度越明显。

3) 预测结果表明，由于1 600 m开火距离以远命中目标破片数期望小于1.0枚，则某高炮武器系统最远开火点距离应不大于1 600 m；与预测结果相比，预测命中破片数与试验结果统计破片数量为19枚相比，误差小于25%，验证了模型的准确性。