基于三粒子和五粒子纠缠态的量子隐形传态通信
2022-08-09苏孙庆南彩珍廖文良雷国伟
苏孙庆,南彩珍,廖文良,雷国伟
(集美大学,福建 厦门 361021)
量子通信利用量子信道对信息进行编码、传输和处理,具有安全性高、信道容量大的特点。量子秘密通信的主要目标是信息安全,主要有量子密钥分发[1]、安全直接量子通信[2]和量子秘密共享[3]等方式。量子纠缠是量子力学中的一种独特现象,是量子力学与经典物理学的最大区别,是量子通信和量子信息处理的重要资源[4],并且已经在量子保密通信方面[5]被广泛应用。量子隐形传输是纠缠的一个重要体现[6],从Bennett等[7]提出第一个单粒子未知态的传输方案之后,量子隐形传态就成为了量子信息研究的重点。从单个粒子量子态的隐形传输发展到多个粒子的隐形传输,再从一般的量子态的隐形传输,发展到受控量子态的隐形传输。可以看出,人们在理论和实验上对量子隐形传态进行了广泛的研究[8-11]。
考虑到量子通信的实际应用,本文提出了基于三粒子纠缠态和五粒子纠缠态的量子隐形传态通信。首先,制备了三粒子、五粒子的纠缠态并给出了相应的量子线路图。然后,基于该纠缠态,提出任意单粒子未知量子态的隐形传态方案和任意二粒子未知量子态的隐形传态方案。前一个方案中,在监察者Monitor的控制下,发送方Sender进行Bell基测量和经典通信;后一个方案中,发送方Sender进行四粒子投影测量和经典通信。最后接收方Receiver采用简单的酉变换就可以以100%的概率成功地恢复原始未知量子态。
1 纠缠态的制备
1.1 三粒子纠缠态的制备
所要制备的三粒子纠缠态为
(1)
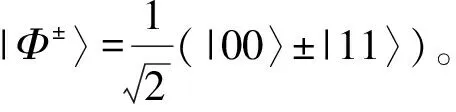
|ζ0〉=|0〉2|0〉3|0〉1
(2)
分别用Hamdmard门和CNOT(受控非门)进行H运算和Cij运算,其中

cij=|i〉|i⊕j〉
(3)
式中⊕是关于模2的加法运算。具体制备步骤如下:
1)对粒子1进行H运算,|ζ0〉变换为|ζ1〉
(4)
2)对粒子(1,2)做一次CNOT运算cij,粒子1作为控制量子,粒子2为目标量子,经此运算后|ζ1〉就变换为|ζ2〉
(5)
3)对粒子2进行一次H运算,|ζ2〉变换为|ζ3〉

|01〉31(|0〉-|1〉)2]
(6)
4)对粒子(2,3)做一次CNOT运算Cij,粒子2作为控制量子,粒子3作为目标量子,经此运算后|ζ3〉就变换为式(1)所示的三粒子纠缠态|Q〉

(|00〉23-|11〉23)|1〉1]=
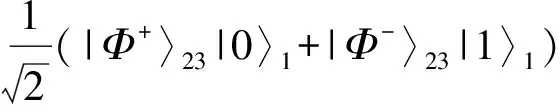
(7)
上式所示三粒子纠缠态的制备过程的量子线路图如图1所示。

图1 制备三粒子纠缠态的量子线路图
1.2 五粒子纠缠态的制备
所要制备的五粒子纠缠态为

|Ψ-〉23|Ψ-〉45|1〉1)
(8)
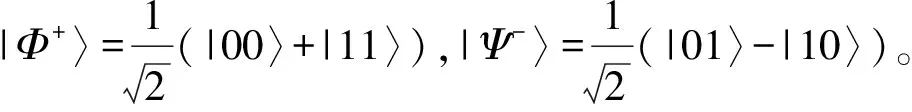
(9)
具体制备步骤如下:
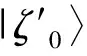
(10)

(11)


(|01〉-|11〉)23(|01〉-|11〉45|1〉1]
(12)


|Ψ-〉23|Ψ-〉45|1〉1)
(13)
上式所示的五粒子纠缠态的制备过程的量子线路图如图2所示。

图2 制备五粒子纠缠态的量子线路图
2 量子隐形传态通信
2.1 任意单粒子量子隐形传态通信
设发送方Sender处,待传送的未知的任意单粒子态为
|ξ〉l=a|0〉l+b|1〉l
(14)
其中,a和b都为复数,且满足归一化条件:
|a|2+|b|2=1。
发送方Sender、控制方Monitor和接收方Receiver共享式(1)中所示的三粒子纠缠态作为量子信道。其中,Sender拥有粒子2,Receiver拥有粒子3,Monitor拥有粒子1。则整个系统的量子态为
|Γ〉=|ξ〉l⊗|Q〉231
(15)
再将式(15)用Bell基表示得
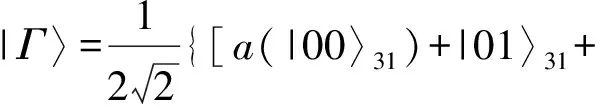
b(|10〉31-|11〉31)]β00〉12
+[a(|10〉31-|11〉31)+b(|00〉31+|01〉31)]β01〉12
+[a(|00〉31+|01〉31)-b(|10〉31-|11〉31)]β10〉12
+[a(|10〉31-|11〉31)-b(|00〉31+|01〉31)]β11〉12
(16)
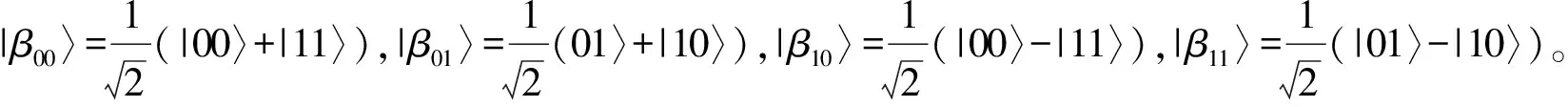
任意单粒子量子隐形传态通信方案可由以下几个步骤完成:
1)Sender对自己所拥有的粒子l和粒子2进行联合Bell基测量,并将结果经由经典信道反馈给Monitor和Receiver。由式(16)可知,Sender获得其中一个测试结果的概率为四分之一。例如:Sender的测试结果若为|β00〉l2,则粒子3和粒子1的态将塌缩为
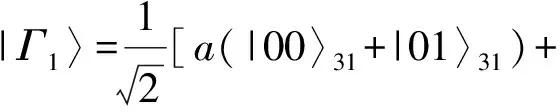
b(|10〉31-|11〉31)]
(17)
2)若Monitor同意Sender和Receiver之间的通信,则Monitor收到信息后,就用计算基{|0〉,|1〉}对自己所拥有的粒子1进行测量,并将测试结果反馈给Receiver。
当Sender的测试结果为|β00〉l2时,若Monitor对粒子1的测试结果为|0〉,则粒子3的态就塌缩为
|Γ2〉=a|0〉3+b|1〉3
(18)
若Monitor对粒子1的测试结果为|1〉,那么式(17)的态就变为
|Γ3〉=a|0〉3-b|1〉3
(19)
3)Receiver收到Sender和Monitor的测试结果后,就可以采用适当的酉变换,重构Sender的原始未知态式(14)。
如果Sender的测试结果为|β00〉l2时,而Monitor对粒子1的测试结果为|0〉时,则Receiver对粒子3执行酉变换I,即可重构原始未知态
I|Γ2〉=a|0〉3+b|1〉3
(20)
若Monitor对粒子1的测试结果为|1〉时,则Receiver对粒子3执行酉变换σz,同样能完成原始未知态的重构
σz|Γ3〉=a|0〉3+b|1〉3
(21)
表1是Sender和Monitor所有可能的测量结果(分别为|βjk〉l2、|Ψ〉1)、粒子3的塌缩态|Γx〉以及Receiver的重构酉变换U之间的对应关系,见表1。

表1 Sender和Monitor的测量结果、塌缩态以及重构酉变换之间的对应关系
不论Sender与Monitor的测量结果如何,Receiver都可以找到对应的酉变换进行重构,使得Receiver的粒子3的量子态与Sender的单粒子未知态具有相同的形式,这就说明量子隐形传态通信总能实现。
对于Sender和Monitor的任何测量,式(14)的原始态总能被成功地传送给Receiver。Sender获得4个可能测量结果中任意一个的概率均为1/4;Monitor得到两种测量结果中任意一种的概率均为1/2,表1中有8种情况,所以该方案成功的总概率为
即该方案的成功概率为100%。
2.2 任意二粒子量子隐形传态通信
设发送方Sender处有待发送的任意的二粒子未知态
|ξ〉mn=(a|00〉+b|01〉+c|10〉+d|11〉)mn
(22)
其中a,b,c,d均为复数,且|a|2+|b|2+|c|2+|d|2=1。Sender、Monitor和Receiver三方共享式(8)所示的五粒子纠缠态作为量子信道。其中,粒子2、4属于发送方Sender,粒子3、5属于接收方Receiver,粒子1属于控制方Monitor。则整个系统的量子态为
(23)
任意二粒子量子隐形传态通信方案可由以下几个步骤完成:
1)Sender对自己所拥有的粒子m、n、2和4进行四粒子Von Neumann测量,并将结果经由经典信道反馈给Monitor和Receiver。其测量基由如下向量构成
|ε0〉=(|0000〉+|0101〉+|1010〉+|1111〉)/2
|ε1〉=(|0000〉-|0101〉+|1010〉-|1111〉)/2
|ε2〉=(|0000〉+|0101〉-|1010〉-|1111〉)/2
|ε3〉=(|0000〉-|0101〉-|1010〉+|1111〉)/2
|ε4〉=(|0001〉+|1011〉+|0100〉+|1110〉)/2
|ε5〉=(|0001〉+|1011〉-|0100〉-|1110〉)/2
|ε6〉=(|0001〉-|1011〉+|0100〉-|1110〉)/2
|ε7〉=(|0001〉-|1011〉-|0100〉+|1110〉)/2
|ε8〉=(|0010〉+|1000〉+|0111〉+|1101〉)/2
|ε9〉=(|0010〉+|1000〉-|0111〉-|1101〉)/2
|ε10〉=(|0010〉-|1000〉+|0111〉-|1101〉)/2
|ε11〉=(|0010〉-|1000〉-|0111〉+|1101〉)/2
|ε12〉=(|0011〉+|1001〉+|0110〉+|1100〉)/2
|ε13〉=(|0011〉+|1001〉-|0110〉-|1100〉)/2
|ε14〉=(|0011〉-|1001〉+|0110〉-|1100〉)/2
|ε15〉=(|0011〉-|1001〉-|0110〉+|1100〉)/2
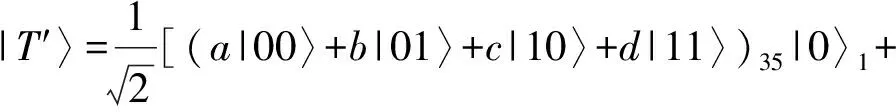
(a|11〉-b|10〉-c|01〉+d|00〉)35|1〉1]
(24)
2)若Monitor同意Sender和Receiver之间的通信,则Monitor收到信息后,就用计算基{|0〉,|1〉}对自己所拥有的粒子1进行测量,并将测量结果反馈给Receiver。
当Sender的测试结果为|ε0〉时,若Monitor对粒子1的测试结果为|0〉,那么式(24)的态就变为:
|T2〉=(a|00〉+b|01〉+c|10〉+d|11〉)35
(25)
若Monitor对粒子1的测试结果是|1〉,那么式(24)的态就变为
|T3〉=(a|11〉-b|10〉-c|01〉+d|00〉)35
(26)
3)Receiver收到Sender和Monitor的测试结果后,Receiver就可以采用适当的酉变换,重构Sender的原始秘密态式(22)。
如果Sender的测试结果为|ε0〉,而Monitor对粒子1的测试结果为|0〉时,则Receiver对粒子3和5执行的酉变换为I⊗I
(I⊗I)|T2〉=(a|00〉+b|01〉+c|10〉+d|11〉)35
(27)
若Monitor对粒子1的测试结果为|1〉时,则Receiver对粒子3和5执行的酉变换为iσy⊗iσy
(iσy⊗iσy)|T3〉=(a|00〉+b|01〉+c|10〉+d|11〉)35
(28)
上述两种情况经过酉变换之后所得结果式(27)和式(28)均为Sender所要传送的原始二粒子未知态。
表2是Sender和Monitor所有可能的测量结果(分别为|εj〉mn24、|Ψ〉1)、粒子3和5的塌缩态|Tx〉以及Receiver的重构酉变换U之间的对应关系。由表2可知,对于每一个测量结果,Receiver都可以找到相应的幺正变换进行重构,使Receiver可以将粒子3和粒子5的量子态还原为Sender的两粒子未知纠缠态。结果表明,无论Sender和Monitor的测量结果如何,Receiver总能重构出式(22)所示的原始未知纠缠态。
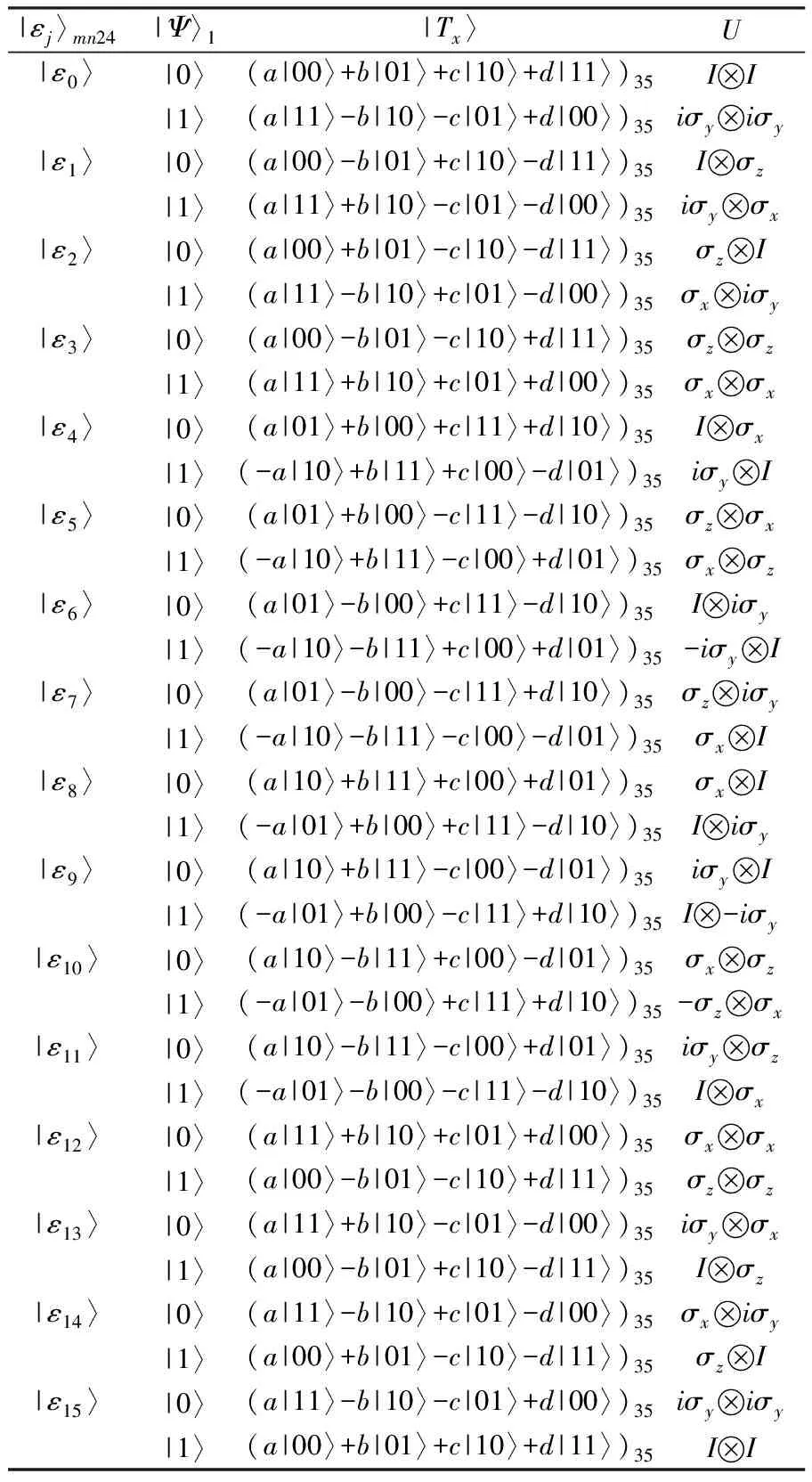
表2 Sender和Monitor的测量结果、塌缩态以及重构酉变换之间的对应关系
此外,还需要考虑的是量子通信任务成功的概率。Sender获得16个可能测量结果中任何一个的概率均为1/16;Monitor得到两个测量结果中任何一个的概率均为1/2,表2中有32种情况,所以该方案的成功总概率为
即本方案的成功概率为100%。
3 结论
纠缠是一种重要的量子资源,不断挖掘和开发各种量子资源对量子通信的发展有着重要的意义。本文用Hamdmard门和受控非门这两种常见量子操作,制备了三粒子和五粒子纠缠态,并给出了相应制备过程的量子线路图。运用三粒子纠缠态的量子信道,实现未知单粒子态的量子隐形传态通信方案。在该方案中,发送方Sender对3粒子纠缠态中自己所拥有的粒子2和处于未知单粒子态的粒子l进行Bell基测量,使得接收方Receiver在控制方Monitor的配合下,只需执行简单酉变换就能恢复原始量子态,其中控制方Monitor对自己所拥有的粒子1运用计算基{|0〉,|1〉}对其进行测量。同时也提出了一种运用五粒子纠缠态的量子信道,以完成任意二粒子未知量子态的隐形传态通信方案。在该方案中,发送方Sender使用16维希尔伯特空间中的一组特殊的完全正交状态作为测量基,实现投影测量(四粒子Von Neumann测量),使接收方Receiver在得到发送方的测量结果和控制方Monitor的配合下,只需再做一个简单的幺正变换(酉变换)就可以恢复原始量子态。另外,测量基的选择使得信息传递过程简单明了,方案成功的概率为100%。二种方案涉及的变换有Hamdmard门、受控非门和Pauli算子、Bell基测量、以及简单的投影测量,这些都能在现代光学技术中实现。而且这两种方案,不论最后塌缩态为何,都有相应的酉变换去重构原始量子态,因此普适性较强。
