“双碳”目标下造纸企业低碳转型的动态演化博弈仿真分析
2022-08-09胡茂斌
周 斌 胡茂斌
1 引 言
2020年9月,习近平总书记在第七十五届联合国大会上提出,争取在2030前中国二氧化碳排放量达到峰值,在2060前实现碳中和(“双碳”目标)。实现碳达峰、碳中和是一场广泛而深刻的经济社会系统变革(王怡, 2022[1])。在当今气候变化日益严峻的形势下,“双碳”目标的提出是中国作为负责任大国的表现之一。完成这个目标,中国必须立足实际,统筹协调好经济、社会、资源等,协同推进低碳、绿色、循环发展(邬彩霞, 2021[2])。2021年国务院印发《关于加强企业温室气体排放报告管理相关工作的通知》确定发电、石化、化工、建材、钢铁、有色、造纸等重点碳排放单位,明确要求各省级生态环境部门对相应企业的碳排放数据进行报送与检查。造纸企业作为唯一的轻工业行业被纳入其中(张杨,胡永钢, 2021[3])。在政策的约束下,发展低碳经济是我国必然趋势,造纸企业进行低碳改造是顺势而为,否则必将会被社会淘汰。造纸企业作为高排放、高消耗的代表,在快速发展的过程中势必会带来高碳排放、能源消耗巨大等环境问题,阻碍造纸企业的发展。由于造纸企业数量较多,改造成本巨大,造纸企业为追求利润最大化,节省成本,往往会采取高碳生产方式,而政府处理企业碳排放问题的部门单一,对于企业碳排放收集工作非常困难,可能存在监管乏力的问题。造纸企业碳排放最主要来源是化石燃料燃烧排放,煤炭能源使用占据化石燃料燃烧的大部分,而造纸企业煤炭几乎全部用于小型自备电厂和供热锅炉,能源利用效率低,生产设备以及技术较为落后,使得造纸企业碳排放量大(李永智等, 2017[4])。造纸企业作为社会重要的组成部分、与我国经济以及人民生活密切相关,应当积极响应国家号召,促进中国低碳经济快速发展。因此,在“双碳”目标的背景下,造纸企业要在保护环境的同时,实现可持续发展,必须要加快自身低碳转型的步伐。
2 文献回顾
目前,国内外许多学者对企业的低碳转型的策略进行研究。Lu等(2019)[5]通过介绍几家大型油气企业低碳转型实践策略,分析了低碳转型路径、机遇和挑战,得出大力发展天然气业务是油气企业向低碳转型过渡的第一步以及加大可再生能源投资的结论。Wu(2016)[6]通过层次分析法和模糊评价方法,从经济效益、环境效益和社会效益三个方面构建了矿山企业低碳转型效益评价指标体系。陆菊春等(2019)[7]从利益视角出发,构建了建筑企业、政府、消费者的低碳转型演化博弈模型,研究了模型的稳定策略以及影响因素,为促进建筑企业低碳转型提出建议对策。赵国涛等(2021)[8]在对“双碳”目标的充分解读基础上,分析了这一政策对火电企业的影响,从多个方面提出应对火电企业低碳转型的策略与方法。徐建中和吕希琛(2014)[9]构建了政府、制造企业和消费者三方演化博弈模型,研究各主体的演化路径与规律,分析制造企业低碳转型各策略稳定性。许莹等(2018)[10]在雾霾的背景下,构建政府监管部门与交通企业的演化博弈模型,得到政府监管力度、查处成功率以及第三方举报率会对交通企业的低碳转型策略的实施产生影响。张宏娟等(2016)[11]以传统制造业集群内的企业为主体,运用动态演化博弈理论,研究能够促进制造业集群内的企业低碳转型的策略建议。
另一方面,国内外也有学者对造纸产业的减少碳排放策略进行了研究。Man等(2020)[12]采用生命周期评估法对中国造纸产业温室气体排放进行评估,以提出减排目标,并找到实现中国造纸产业减排目标的途径。吕泽瑜等(2017)[13]分析了我国现阶段造纸企业碳排放的现状,来寻找有效的技术与策略来实现碳减排,并得出我国未来造纸企业排碳任务艰巨,造纸企业要想实现可持续发展,需要促使企业优化能源使用结构。王思文和任启芳(2019)[14]等在循环经济背景下,就环保部门与造纸企业之间建立排污博弈模型,通过三阶段的讨价还价博弈,对造纸企业排污、治污问题提出相应的建议与对策。
综上所述,已有的研究文献对不同条件下不同类型企业的低碳转型路径进行研究,国内外学者只针对造纸企业的碳排放、碳管理以及排污进行了研究,并没有涉及到造纸企业低碳转型路径的研究。然而,随着我国“双碳”目标的不断进行,以及造纸企业碳排放问题的存在,发展低碳经济,促进造纸企业低碳转型刻不容缓。因此,本文以造纸企业为研究对象,使用动态演化博弈模型探究其低碳转型的路径,通过建立政府部门与造纸企业的动态演化博弈模型,研究造纸企业低碳转型的稳定性策略以及影响因素,从而为造纸企业低碳转型提出建设性意见,具有研究内容的创新性与积极的现实意义。
3 演化博弈模型构建
3.1 基本假设
假设1:根据演化博弈理论基础,假设博弈的两个主体政府与造纸企业均是有限理性的,且都在追求自身利益最大化。
假设2:政府的行为策略为{监管、不监管},其采取“监管”策略的概率为x(0≤x≤1),采取“不监管”的策略为1-x。造纸企业的行为策略为{低碳生产、高碳生产},采取“低碳生产”的概率为y(0≤y≤1),采取“高碳生产”的概率为1-y。
假设3:政府会对造纸企业低碳生产进行监督,监管成本为b1,政府对造纸企业进行监管时,会对高碳生产企业处以一定的罚金n,给低碳生产企业给予补助m。政府作为公共管理部门,对社会承担着一定的责任,当造纸企业进行高碳生产时,需要对环境进行治理,治理成本为b2。
假设4:造纸企业进行低碳生产的基本收益为p,造纸企业低碳改造成本为c,同时低碳生产会给造纸企业带来额外收益g。造纸企业选择进行低碳生产,政府会获得一定收益r,主要包括环境改善以及上级政府对于碳排放量降低的奖励等。
基于以上的假设,可以构建造纸企业与政府的收益矩阵,如表1所示。

表1 政府与造纸企业的收益矩阵

3.2 博弈模型稳定性分析
将所得的均衡点代入雅可比矩阵J,结果如表2所示:

表2 系统局部均衡点的稳定性分析
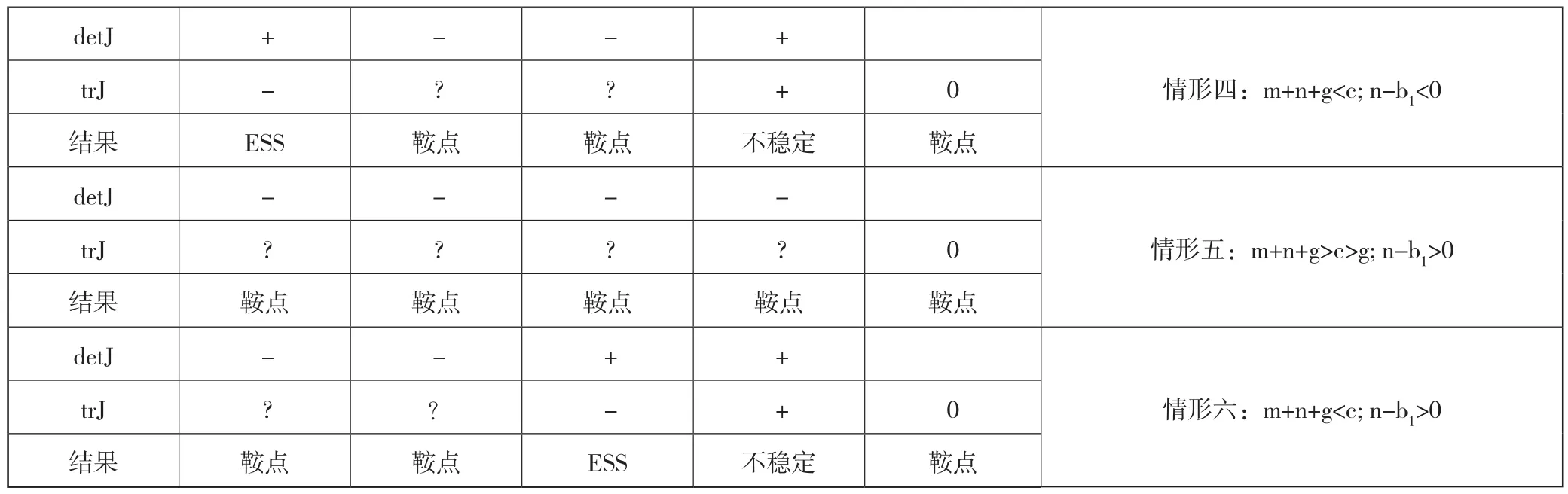
续表
4 政府与造纸企业演化博弈分析
4.1 路径分析
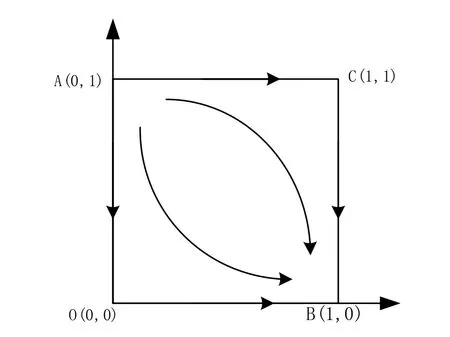
当g-c>0且n-b1<0(或者n-b1>0)时,系统演化结果都为(不监管,低碳生产)。在这两种情形下,造纸企业采取低碳生产策略所获得额外收益大于企业自身进行低碳改造成本,对于造纸企业来说,这即能够使企业获利,又符合政策的要求,让企业有利可图,因此将选择“低碳生产”策略。政府监管成本无论大于还是小于政府对高碳生产造纸企业的罚金,政府都会选择“不监管”的策略。这种状态出现在整个行业的后期,对政府来说,是非常乐意看到的,即使不监管企业也会进行低碳生产。这时,大多造纸企业都已经转型成功,造纸企业碳排放量较少,而对企业的低碳补贴是非常的大,无论政府监管成本如何,政府的整体支出远远大于收益。造纸企业与政府演化相位图如图1所示。

图1 情形一与情形二相位图
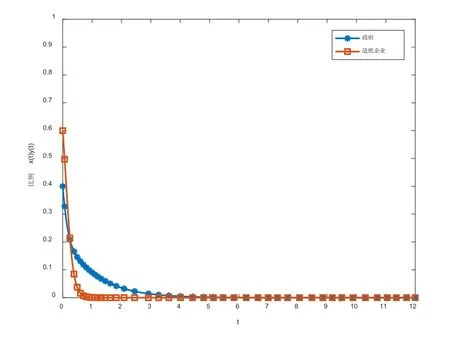
当n-b1<0且m+n+g>c>g(或者m+n+g 图2 情形三与情形四相位图 当m+n+g>c>g且n-b1>0时,系统最终演化结果没有稳定点,不存在演化稳定策略。博弈双方策略的选择是紧密依赖、相互影响的,一方策略的选择依赖于另一方策略的选择的预测,一个参数的变化或者其他因素考虑其中,都会使双方策略选择处于不确定的状态。该状态出现在造纸行业低碳转型的中后期,政府与造纸企业双方互相在考虑对方的策略,政府考虑已经实施了监管后,造纸企业是否要进一步对企业进行低碳改造,从而进行低碳生产。造纸企业则考虑政府的监管是否会一直持续下去,如果一直监管,而自身不实施低碳改造进行低碳生产,所受罚金会远远高于低碳改造成本,企业会出现入不敷出的现象。为了更明确博弈双方策略的选择倾向,由相位图图3可知: 图3 情形五相位图 如果初始点落在Ⅰ区域,系统将收敛于(1,0),政府与造纸企业将会选择(监管,高碳生产)策略。在该条件下,政府实施“监管”的概率较小,企业预测政府将会实施“不监管”策略,因而造纸企业选择“高碳生产”。而企业在该条件下实施“低碳生产”的概率较小,政府预测造纸企业大概率会实施“高碳生产”,因而政府会选择“监管”策略;如果初始点落在Ⅱ区域,系统收敛于(1,1),政府与造纸企业将会选择(监管,低碳生产)策略。在该条件下,政府实施“监管”策略的概率较大,企业预测到政府实施的策略,因而造纸企业会选择“低碳生产”策略,企业在该条件下实施“高碳生产”的概率会比实施“低碳生产”概率大,政府预测企业会实施“高碳生产”,因而会选择“监管”策略;同理可得,当初始点落在Ⅲ区域,系统收敛于(0,1),政府与造纸企业将会选择(不监管,低碳生产)策略。初始点落在Ⅳ区域,系统收敛于(0,0),政府与造纸企业会选择(不监管,高碳生产)策略。 当m+n+g 图4 情形六相位图 为了进一步分析政府在不同监管成本、处罚罚款与低碳补贴、企业低碳改造成本条件下,政府与造纸企业低碳转型的演化稳定策略,运用Matlab对政府与造纸企业五种情形下行为策略演化过程进行数值仿真分析。 (1)当g-c>0;n-b1<0时,对各参数进行取值m=4,n=3,g=3,c=2,b1=4,所得的动态演化趋势如图5所示。随着时间t的推移,政府选择监管策略的概率越来越小,造纸企业选择低碳生产的概率越来越大,演化系统最终呈现出稳定的结果:(不监管,低碳生产)。当政府对造纸企业的监管成本大于其对企业的高碳罚金时,政府最终趋向选择不监管。造纸企业为了自身长期发展从而趋向于进行低碳改造进行低碳生产。 图5 情形一动态演化趋势 (2)当g-c>0;n-b1>0时,对各参数进行赋值m=4,n=3,g=3,c=6,b1=1,所得到的动态演化趋势如图6所示,演化系统最终呈现出的稳定结果:(不监管,低碳生产)。当造纸企业低碳改造的额外收益大于低碳改造成本时,即使政府在不监管的情况下,造纸企业也会趋向于进行低碳生产。 图 6 情形二的动态演化趋势 (3)当m+n+g>c>g;n-b1<0时,对各参数进行赋值m=4,n=3,g=3,c=6,b1=4,所得到的动态演化趋势如图7所示;当m+n+g 图7 情形三动态演化趋势 图8 情形四动态演化趋势 (4)当m+n+g 图 9 情形六动态演化趋势 本文基于当前政策与现实热点,运用演化博弈的相关理论,建立政府与造纸企业的动态演化博弈模型,运用Matlab软件对政府与造纸企业在不同情形下演化路径进行数值仿真。研究结论如下:(1)政府与造纸企业低碳转型的演化过程与政府监管成本b1,造纸企业低碳改造成本c的取值密切相关,其他变量的取值不变的情况下,随着b1与c取值的不同,博弈双方呈现出不同的状态;(2)在条件g>c且n>b1(或n 基于本文的研究结论,提出如下建议:(1)完善政府的监管职能,优化与创新政府监管机制,降低政府监管成本。政府的监管是造纸企业低碳转型过程中重要的一环,政府监管成本高低,会影响政府对造纸企业监管策略的选择。降低监管成本必须依法行政,建立与强化对造纸企业低碳监管法规,使政府的一切监管决策与行为都具有基本规范与约束,从而各级行政机关各司其职,即保障造纸企业的合法权益,又使得政府各项监管成本大大降低。同时,政府需要通过一系列措施来降低监管成本,设置市民举报机制、引用第三方监督机构、设立碳排放监管委员会等。做好造纸企业低碳生产的巡查工作,推行网上监管政务:罚金缴纳与奖励发放、碳排放以及污染排放网上数据实时检测、国家以及地区政策法规的更新完善通知等。另外,制定监管政绩考核,政府对企业监管支出需要遵循成本-效益原则,将企业监管成本纳入政府官员政绩评价中去;(2)加强造纸企业科技创新,探索低碳技术新方式。造纸企业低碳改造成本高低会影响造纸企业低碳转型策略的选择,而企业降低低碳改造成本必须依靠自身科技创新。但一般的企业在这方面由于资金不足以及创新积极性不高而被淘汰,因此政府应该加大对造纸企业的补贴,提供足够的资金支持。科技人才是企业自主创新,不被社会淘汰的关键,更何况在“双碳”目标背景下,造纸行业竞争日益激烈。因此,造纸企业可以通过吸引海内外高层次人才,充分调动科研人员积极性与创造性,打造一支实力强、素质高、技术硬、制度合理的创新人才队伍,不断对造纸企业高碳排放设备以及污染处理设备进行低碳技术改造。同时,造纸企业可以与各大高校以及各研究机构合作,形成校企合作或研企合作的局面,为造纸企业低碳改造与转型提供创新方法与技术支撑;(3)构建新型碳排放补贴与惩罚机制。由于造纸企业低碳改造后期阶段,政府对造纸企业的补贴过于大,使得政府的收益远不及支出,而在低碳改造前期,对于造纸企业高碳生产惩罚力度不强,使得造纸企业前期对低碳改造没有采取任何措施。因此,在整个造纸企业低碳改造的过程中,政府对造纸企业的补贴与处罚需要及时改进与更替,一方面可以通过成立碳排放专业评估小组,积极探索整个地区碳排放的核算办法与标准,为政府对企业的补贴以及高碳处罚设立合理的标准;另一方面发挥市场在政府与造纸企业的动态演化博弈中的调节功能,以碳排放交易替代政府财政补贴,形成市场化激励与惩罚机制。





5 结论与建议
