政府补贴、研发投入与全要素生产率
——中国制造业企业的实证研究
2022-08-09任宇新张雪琳吴敬静贺正楚
任宇新 张雪琳 吴敬静 贺正楚
1 引 言
我国经济已步入高质量发展阶段,转变发展方式、优化经济结构、转换增长动力、提高全要素生产率成为新发展阶段的重点目标和主要任务。在制造业领域,中国虽然是制造业大国,但表现出“大而不强”的特点,长期居于全球价值链的中低端,从事低附加值、劳动密集型产业,中国制造业大国还面临创新能力要加强 和技术进步要加快的巨大竞争压力。因此,以创新能力、技术进步为主的发展模式下,提升制造业企业全要素生产率应成为实现经济高质量发展的题中之意。根据马克思理论,经济增长方式为内涵扩大再生产与外延扩大再生产。内涵扩大再生产通过科学管理与技术进步提高使用效益与生产要素质量;外延扩大再生产需要投入人力、财力和物力等生产要素,以实现经济增长与生产规模扩大。依据新古典经济学理论,外延扩大再生产有以下不足:一方面外延扩大再生产所需的投入要素在短时间内很难发生质的变化;另一方面依赖要素投入取得的经济增长会导致边际报酬递减。运用内涵扩大再生产的技术创新提高生产率,才能从根本上实现经济高质量发展。因此,技术创新是全要素生产率的本质,提高全要素生产率,是创新作为引领发展第一动力的体现(刘志彪,2018[1];袁晓玲等,2019[2])。
对企业而言,发展源动力的关键是技术创新,研发投入是技术创新的主要载体。一般来说,企业随着知识的积累和研发强度的加深,可逐步提升全要素生产率,促进经济增长。从已有研究来看,研发投入与全要素生产率之间的影响效应存在不同结论,这可能与研究对象、全要素生产率测算方法和实证方法的不同有关,所以运用制造业上市公司微观数据研究企业研发投入与全要素生产率的作用关系具有重要意义。近年来,我国企业研发经费中政府所占部分保持增长势头,这是由于企业研发投入具有外部性,技术产品容易模仿式创新,研发全部收益难以被企业所独享,企业创新积极性易受到挫伤,为矫正企业研发的外部性,政府对企业实施有效调节,通过补贴弥补企业账面应有的研发收益,实现企业账面的平整。但也有学者研究发现,政府补贴会挤出或替代企业自由研发投入(张杰等,2015[3]),政府补贴对企业研发的影响效应较小。在政府补贴逐渐增加环境下,政府补贴发挥的效应如何?政府制度的优越性是否有效发挥?这些问题有待深入研究。为此,本文拟在三个方面实现突破之后得到创新点:一是在研究视角方面,探索政府补贴、研发投入和全要素生产率三者的作用机制,解释三者作用关系,而现有研究只是单纯探讨政府补贴或研发投入对全要素生产率的作用方式,并未打破政府补贴、研发投入和全要素生产率三者的黑箱。二是在定量分析上,国内目前大多采用OP法和LP法估计企业全要素生产率,本文采用国际前沿ACF法(任曙明和吕镯,2014[4])。ACF法可消除OP法和LP法的内生性和不识别性情况,将劳动投入引入中间投入函数,提高结果准确性。三是在研究结论方面,以政府补贴和融资约束为门槛变量,股权集中度为调节变量,实证分析政府补贴、研发投入和生产率三者之间的作用机制,加深对政府补贴效果的认识,实行针对性和差异化的补贴额度,以提升补贴政策的成效。
2 理论基础与研究假设
2.1 政府补贴对研发投入的影响
政府补贴与研发投入存在双向关系。政府通过弥补企业账面亏损以增加盈利,同时弥补由于研发投入的外部性导致研发收益不被企业独享而降低的利润,增加企业研发投入的积极性。但当政府补贴规模过大时,企业可能产生套取补贴的寻租动机,减少企业创新性行为,对企业研发产生负向影响。因此,伴随政府对企业补贴的加大,政府对企业研发并非单纯的线性关系,具有门槛效应(朱金生和朱华,2021[5];李晓钟和徐怡,2019[6];张辉等,2016[7])。制造业上市企业研发项目资金需求较大,相比于其他投资,更易受融资约束的抑制作用(康志勇,2013[8];王海杰和安康,2021[9];刘文琦等,2018[10];张秀峰等,2019[11]),所以考虑在融资约束的背景下,将政府补贴对企业研发投入的影响分为三个阶段。第一阶段:在政府补贴强度较低情况下,政府补贴均促进高、低融资约束企业的研发活动,但低融资约束企业比高融资约束企业促进效果弱。主要体现以下三点:一是政府补贴可以缩短因研发外部性导致企业自身收益与社会收益的差距(吴超鹏和唐菂,2016[12]);二是高融资约束的企业可能存在具有广阔发展前景的研发项目,但由于风险性和信息不对称性使得企业的研发活动停滞不前,企业的创新研发得不到开展,如果此时政府增加补贴力度,能有效激发企业研发动力,并可继续开展受资金约束而停滞的项目,增加高融资约束企业的研发投入;三是政府直接补贴企业会向市场传递信号(Wu,2017[13]),这种信号有利于面临融资约束的企业从金融机构获得更多的融资,促进企业开展创新研发活动。造成这种结果的原因是:政府对企业实施补贴前,会从技术前沿性、研发可行性和可获得的经济效益等诸多因素对企业评估,政府相比金融机构可以掌握更多企业的研发部门信息。当政府对企业予以补贴时,金融机构从政府行为中获得信息,即该企业能以较低的创新研发风险获得较高经济收益(王刚刚等,2017[14]),增加金融机构与企业互信度,拓展企业融资渠道,促进企业创新研发。而低融资约束企业仅面临因研发外部性导致企业自身收益低于社会收益的问题,严格的知识产权保护可以解决技术产品的模仿式创新,初步缩短自身收益和社会收益的差距。因此,政府直接补贴对高融资约束企业促进作用更大,在这一阶段,企业面临融资约束越高,政府对企业研发活动的正向效应越大。第二阶段:伴随政府对企业补贴强度加大,跨越门槛值,随着政府补贴强度增加,政府补贴对融资约束处于高、低区间的企业研发投入的有利影响会不断增强。在此阶段,政府补贴未产生挤出效应(José Ángel Zúñiga‐Vicente,2014[15]),高、低融资约束企业研发资金并不充足,政府加大强度补贴,对高、低融资约束企业研发投入均产生促进效果,因此第二阶段高、低融资约束企业比第一阶段高、低融资约束企业促进效果更强。第三阶段:伴随政府补贴强度的继续加大,跨越下一门槛值,其对高、低融资约束组的促进作用会减弱。主要体现在以下两点:一是较高的政府补贴会使高、低融资约束企业资金充裕,当企业有充足资金流时,补贴资金对研发投入的促进作用会减弱;二是我国市场化改革以稳定经济战略、引导经济发展为目标,资源配置方面受地方政府主导,致使资源配置的管制和干预现象频繁出现。因此,政府加大补贴力度,会导致不同融资约束区间的企业为了获得充足的资金流,与地方政府构成寻租关系(董小红等,2022[16];应千伟和何思怡,2022[17]),并进一步保持寻租关系以获取有利资源,而不是通过自身创新研发提高企业竞争力。因此,提出假设:
H1:以融资约束为门限变量,在不同融资约束强度中,政府补贴对研发投入的影响效应不同。
H2:当政府补贴强度较低时,政府补贴对高、低融资企业起到促进作用,并且高融资企业促进作用大于低融资企业。
H3:当政府补贴强度较高时,政府补贴对高、低融资企业发挥的正向效应减弱,甚至可能没有影响。
2.2 研发投入对全要素生产率的影响
国内关于研发投入强度、研发补贴、创新要素投入与全要素生产率关系的研究较多。目前学术观点主要分为如下几类:一是正向关系论,认为研发投入对全要素生产率起到正向促进作用(王宛秋和邢悦,2017[18];刘晔和林陈聃,2021[19];王晓娆和李红阳,2017[20]);二是负向关系论,认为研发投入对全要素生产率起到负向抑制作用(李小平和李小克,2018[21])。根据内生增长理论,企业内生技术进步的唯一途径是提升全要素生产率,而制造业企业研发投入比较集中,是技术创新的主要载体。基于此,本文认为制造业企业研发投入能正向提升企业全要素生产率:一方面,企业开展研发活动学习技术、积累知识,这些技术和知识增加企业新产品研发经验和产品技术含量,提高员工创新能力;另一方面,研发投入的增加可引进更多新设备、新产能和新的生产管理方式,优化资源配置效率,先进生产要素在不同部门间流动,从而提升企业全要素生产率。因此,提出假设:
H4:研发投入对企业全要素生产率起到正向促进作用。
2.3 股权结构对研发投入和全要素生产率关系的调节效应
现有文献主要从两职合一(张广胜和孟茂源,2020[22])、政治关联(张广胜和孟茂源,2020[22])、外商投资(李晓钟和王倩倩,2014[23])、出口(谭朵朵和岳倩,2022[24])等角度对企业研发投入和全要素生产率的关系进行研究。企业全要素生产率的提升离不开公司治理,股权结构是公司治理的基础,所以研究股权结构对研发投入和全要素生产率二者关系的影响具有现实意义,本文采用股权集中度衡量股权结构。股权集中度与研发投入的关系,学术界有三种观点:一是正向促进作用,认为股权集中有利于研发投入(任海云,2010[25]);二是负向抑制作用,过高股权集中会抑制研发投入转化效率(沈毅和张清正,2020[26]);三是股权集中度具有门槛效应,只有当股权集中程度超过一定门槛时,才会对研发投入产生抑制或促进作用(王春丽和马路,2017[27]);四是倒U型关系或U型关系,股权分散致使企业内部管理效率降低,研发创新进程减缓,而股权过于集中又将导致大股东权力过大操控企业行为,因此股权集中度对研发投入的影响呈阶段性特征(冯根福和温军,2008[28];刘胜强和刘星,2010[29])。五是其他曲线关系,比如股权集中度与研发投入呈N型曲线关系(李经路,2017[30])。
我国制造业发展规模较大,但仍存在产业结构不平衡、部分领域缺乏核心技术等问题,加强制造业企业研发能力应是发展重点。若各个股东持股比例差距较小,企业股权分散,股东对企业管理权限保持平衡态势,会增大企业代理成本、增加企业信息不对称性,进而提高企业的决策风险,出现“搭便车”行为,不利于公司运营发展。若企业集中股权,可抑制“搭便车”行为,提高公司监控动机和能力,降低公司代理成本并解决信息不对称问题,为研发活动提供长久支持,深化企业研发创新行为,进而推动企业全要素生产率。因此,提出假设:
H5:股权集中度对研发投入和全要素生产率之间的关系起到显著正向调节作用。
框架研究模型如图1所示:

图1 理论模型与研究假设
3 数据说明与模型构建
选取2013-2020年我国A股上市制造业企业为研究样本,数据来源于Wind数据库、国泰安数据库、巨潮咨询网及上市公司年报。对所选样本作如下处理:剔除ST和*ST企业;剔除政府补贴、研发投入等主要变量的连续缺失值和异常的企业;剔除财务杠杆大于1的企业,这些企业已资不抵债,研究意义较低;为避免极端值影响,对所有指标1%缩尾处理。最终获取3968个观测个体,形成496家上市公司2013-2020年平衡面板数据。
3.1 政府补贴对研发投入的门槛效应
针对个体效应面板模型的研究(Hansen,1999[31]),探究政府补贴与研发投入的门限效应,分别选定政府补贴和融资约束为门限变量,根据所求门限值对回归模型进行划分,检验在不同门限区间内,政府补贴对研发投入的影响效应,首先考虑单一门限模型情况:

式(1)中,RD表示研发投入强度,是被解释变量;SUB表示政府补贴强度,是解释变量。α0是截距项,α1、α2、β是变量系数,SUB是门槛变量,γ是待估计的门限值,εit表示随机误差项,I(*)是示性函数,当括号内关系满足时,取值1,否则取0。Z为控制变量,用来表示影响研发和全要素生产率的因素,参考现有文献,选取如下指标(陈玲和杨文辉,2016[32];王曦和杨博旭,2022[33]):企业规模(SIZE)表示企业的抗风险能力、经济基础和创新动力,中、小型企业为了提升自身竞争力,对研发和创新有强烈需求,但其风险承担能力和经济基础薄弱,而大企业则相反;利润率(PR)表示企业产生的利润越高,用于研发投入的项目就越多;总资产收益率(ROA)可用来表示企业绩效对企业研发投入产生的影响;资本密度(CAP)可将企业归类为资本要素密集度类型或劳动要素密集度类型,不同类型企业对研发要求不同;财务杠杆(LEV)是反映企业财务状况的重要指标,资产负债率大于1 的企业已经资不抵债,企业难以有资金进行研发和创新。
在单一门槛的基础上,以融资约束为门槛变量,政府补贴为核心变量,考虑建立双重门限值的回归模型,双门槛设定模型如下:

式(2)中,FC表示融资约束,采用“利息支出/固定资产净额”衡量(孙灵燕和李荣林,2012[34];李翘楚和成力为,2019[35]),值越小,融资约束程度越大,企业获取资金难度越高。反之,值越大,融资约束程度越小。
运用模型进行双重验证:一是验证门槛是否存在,二是验证门槛是否真实。
假设一:α1≠α2,门槛效应存在
假设二:α1=α2,门槛效应不存在
在门槛效应存在的基础上,进一步确定门槛估计值是否等于其真实值,其假设分别为:

表1 变量设计
3.2 研发投入与全要素生产率基准回归模型
研发投入与全要素生产率之间的作用机制,构建模型1:

股权集中度在研发投入和全要素生产率之间的调节关系,构建模型2和模型3:

TFP表示全要素生产率,是被解释变量;RD表示研发投入强度,是解释变量;CR1表示股权集中度,是调节变量,反映企业治理结构,用第一大股东持股比例表示,比例越高管理者决策监督力度越大;参考现有文献(岳宇君和张磊雷,2020[36];王欢芳等,2020[37]),选取如下指标为控制变量:企业年龄(Age)表示企业生产经验,年龄越大,经验越足;GROWTH是公司经营状况,用营业收入增长率来表示,反映企业发展状况和成长阶段;CASH是资金储备率,用货币资金与总资产的比值来说明,表示企业实际可动用的资金,反映企业的投资状况是过度还是不足;其他控制变量说明见上文。此阶段变量设计如表2。

表2 变量设计
3.3 生产率的测量:ACF法
同时性偏误一直是测量全要素生产率的难题。国内大多采用OP法、LP法和OLS法来解决这个难题(鲁晓东和连玉君,2012[38]),极少应用更准确的ACF法进行测算。OP法(Olley 和Pakes,1996[39])是基于结构模型的半参数法,它将企业的投资水平作为全要素生产率的代理变量,从而消除同时性偏误,但公司投资与全要素生产率严格单调递增是OP法的前提,需保证企业投资水平不可以为0,而企业日常投资量常常为0,这就使投资不是完全影响全要素生产率的代理变量。针对这个问题,Levinsohn等通过提出LP法对OP法进行改进(Levinsohn和Petrin,2003[40]),将中间品投入指标作为代理变量,避免数据截断,LP法比OP法更精确。
OP和LP法都假设企业面对生产率冲击时能够对投入进行无成本的即时调整。而Ackerberg等(2006)[41]以及Ackerberg等(2007)[42]认为企业中间品投入指标受劳动、生产率和资本影响,这说明LP法和OP法在估计全要素生产率上会出现内生性问题。Ackerberg,Caves,Frazer通过放宽LP法和OP法的假设条件,提高结果的准确性。因此,本文应用Ackerberg,Caves,Frazer的方法(简称ACF法)估计全要素生产率,并使用LP法做稳健性检验。
假设企业i的中间投入指标是mit,在时间t内,中间投入受到生产率ωit、资本kit和劳动lit的影响,其函数表达式为:


运用GMM理论求得和,代入公式(10),可求得全要素生产率。用stata17编程实现上述过程。
4 实证分析
4.1 变量描述性统计
如表3所示,上市公司数据中生产率均值是3.815,最大值与最小值之间差值为2.18,标准差是0.253,表明我国制造业上市企业全要素生产率稳定性较弱,分化情况严重。
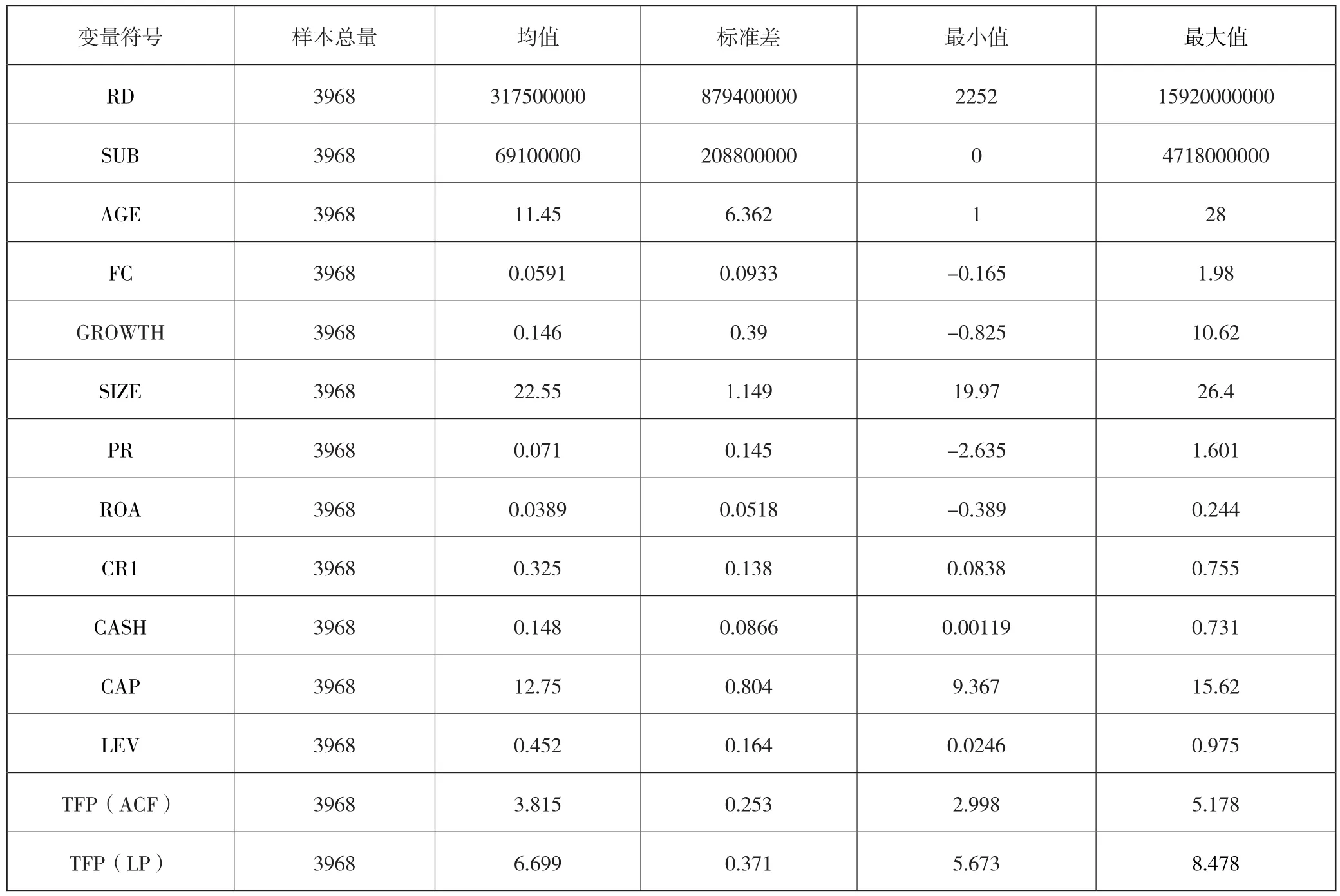
表3 主要变量的描述性统计
样本企业研发金额最大值与最小值金额相差悬殊,将样本数据按行业分类,发现高新技术行业研发投入金额远远高于其他行业。其他行业出现研发投入较低的原因有如下三点:一是公司规模较小,企业资金不足以提供高额研发收入;二是行业自身仅有较低的研发要求;三是企业管理层更重视经营方面。
样本企业整体政府补贴金额最大值为471800万元,政府对于不具备研发创新潜力的企业补贴为0,标准差达208800000,这表明制造业企业得到的政府补贴金额相差悬殊,将数据按行业分类,发现高新技术企业是各地方政府重点扶持的企业,在申请政府补贴上会相对容易;由于政府补贴需要根据企业实际情况发放金额,所以企业规模对申请政府补贴这方面也有很大影响。
样本企业整体股权集中度最大值0.755,最小值为0.0838,标准差为0.138,相差悬殊,说明各个公司的股权结构不尽相同,均值为0.325,说明样本企业之间股权相对集中。
4.2 相关性分析
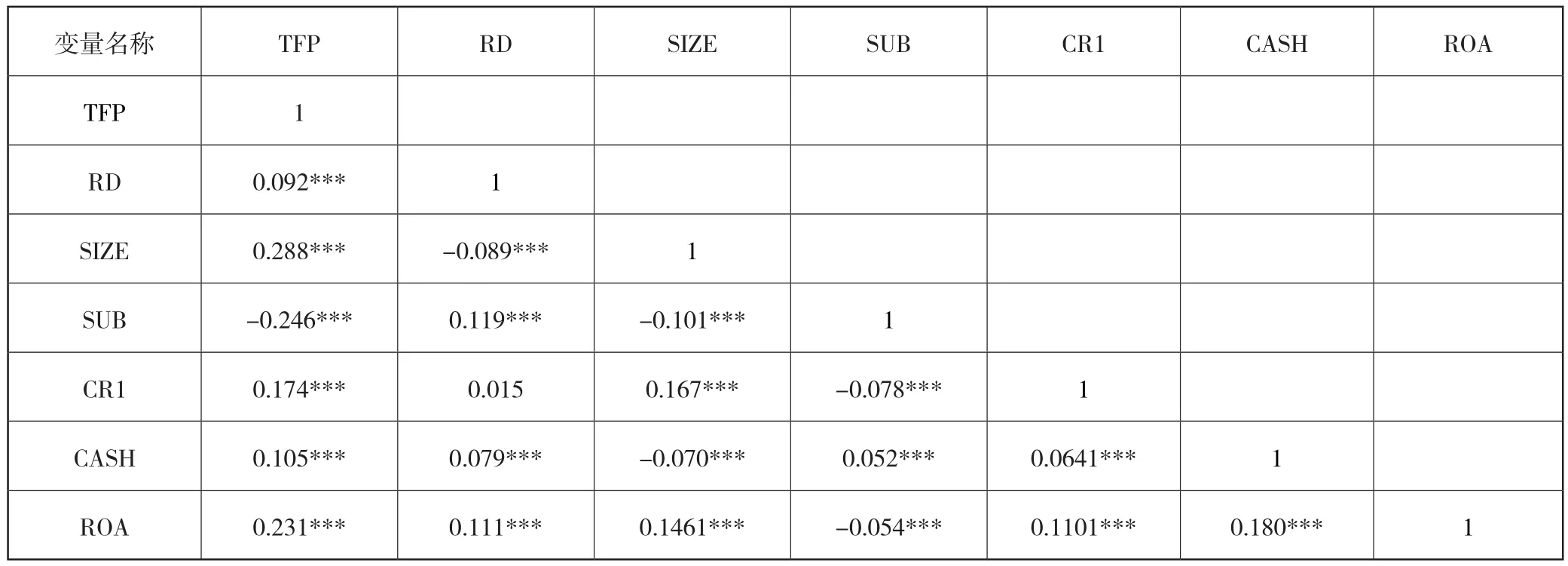
表4 主要变量的相关性分析
由检验结果可知:变量间的相关系数都不大,均小于0.3,7个变量中,企业规模(SIZE)与全要素生产率(TFP)相关系数最高,为0.288。 研发投入正向影响全要素生产率,回归系数为0.092,在1%水平上显著,初步验证假设4。股权集中度与全要素生产率是正向促进关系,回归系数为0.174,在1%水平上显著,说明企业股权越集中生产率越高,初步验证假设5。各个变量之间基本上显著相关,为实证分析打好基础。
4.3 回归分析
运用门槛回归模型实证检验政府补贴、融资约束对研发投入的影响是否会发生突变。
(1)以政府补贴作为门槛变量
当研发投入强度(RD)作为为被解释变量,对496家上市公司制造业企业政府补贴强度 SUB 不存在门槛值、存在一个门槛值以及存在两个门槛值分别进行估计,借鉴Hansen B.E的“自助法(bootstrap)”(Hansen B.E,1999[31]),运用State17.0统计软件,反复抽样300次得出F值和P值,对门槛存在性进行检验,如表5。

表5 检验结果
由表5可知,当政府补贴为门槛变量,得到以下结论:F统计量无论是在单一门限、双重门限还是三重门限模型中,只有单重门限在5%水平上显著,即P值小于0.05,因此模型中存在单一门限值,门限值为0.0002。表6为以政府补贴为门槛变量的回归结果,不同的政府补贴取值对研发投入的影响存在较大差异。当政府补贴强度较小时(SUB≤0.0002),对研发投入的影响系数高达45.577;当政府补贴强度较大时(SUB>0.0002),回归系数变为0.022,且以上两个系数均在5%水平上显著。由此可知:对于我国制造业上市企业,政府补贴对研发投入的有利影响会随着政府补贴强度的加大而减小,虽一直起到促进作用,但促进作用效果有所减弱。原因在于:第一阶段的政府补贴强度刚好可以弥补企业开展研发活动造成的私人收益与社会收益的差距,激发企业开展研发项目的积极性,但当政府补贴强度较大时,可能存在对企业研发活动知识外溢补偿过度的现象,致使比政府补贴强度较小时的促进效果差。

表6 门槛模型回归结果
(2)以融资约束为门槛变量
上述实证只能验证政府补贴对研发投入的影响,而制造业上市企业研发项目资金需求较大,相比于其他投资,更易受融资约束负面影响。本文继续研究政府补贴和融资约束对研发投入的影响效果。
当研发投入强度(RD)作为为被解释变量,政府补贴(SUB)为解释变量,对496家上市公司制造业企业融资约束(FC)不存在门槛值、存在一个门槛值以及存在两个门槛值分别进行实证分析,如表7。

表7 检验结果
由上表可知,以融资约束为门槛变量,模型中存在两个门槛值,均在5%水平上显著,假设1得到验证。门槛值估计结果如表8。

表8 门槛值估计结果
根据回归结果,得出两个门限估计值在95%置信区间的似然比估计图,如图2,门限估计值是似然比统计量LR趋近于0时对应的γ值,图2为2个门槛估计值0.0675和0.0078在 95%置信区间下的似然比函数图。LR统计量最低点为真实门槛值,虚线表示临界值为7.35,由于临界值7.35明显大于2个门槛值,认为上述门槛值真实有效。


图2 双门槛估计结果
表9为以融资约束为门槛变量的面板门槛回归结果,在不同的融资约束取值下,政府补贴对研发投入的影响存在较大差异。当融资约束很宽松时(FC≤0.0078),政府补贴对研发投入影响系数为0.0938;当融资约束较宽松(0.0078
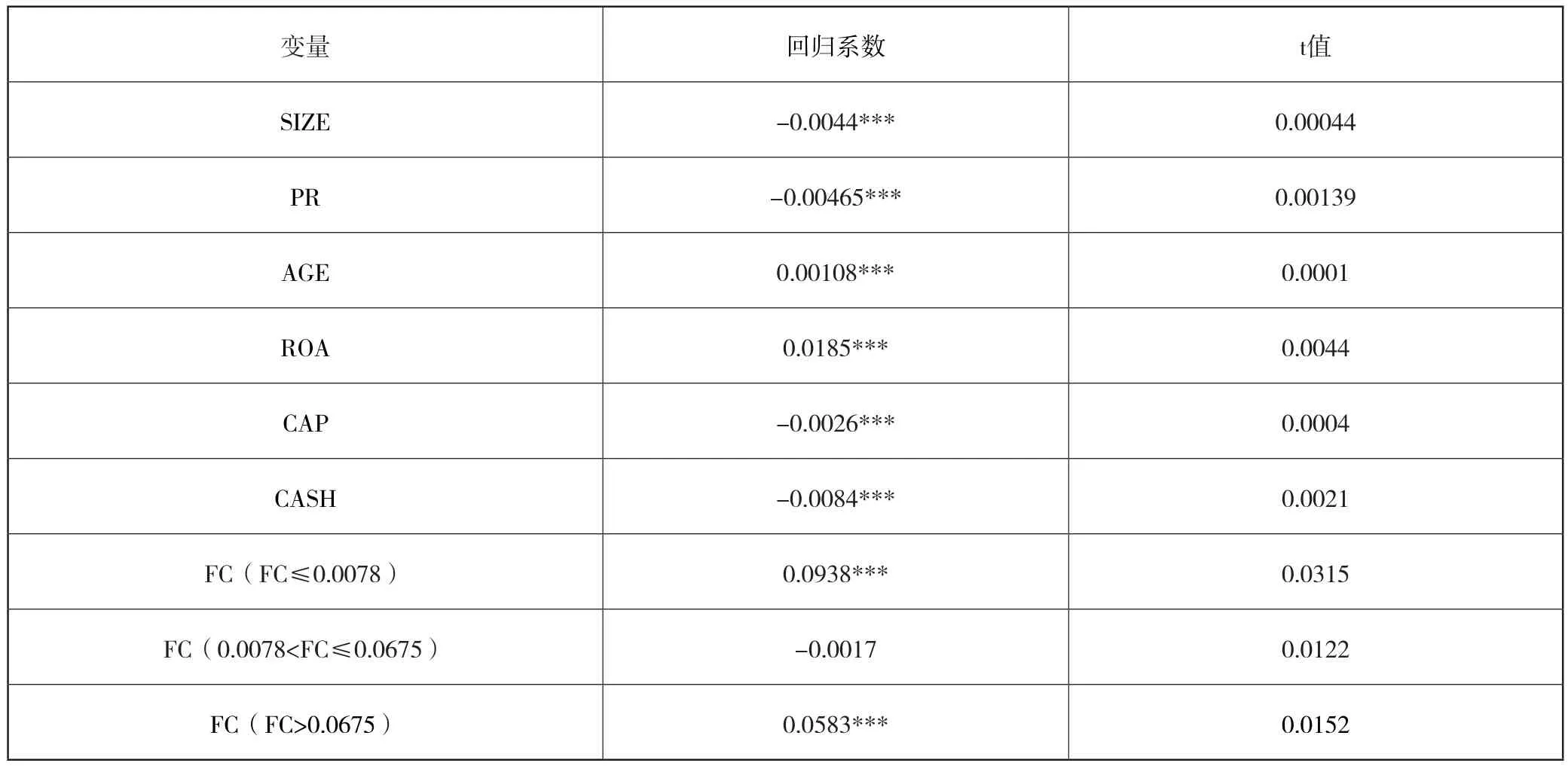
表9 门槛模型参数估计结果
(3)验证政府补贴在高、低融资约束企业中对研发投入的影响
当研发投入强度(RD)作为被解释变量,政府补贴(SUB)为解释变量,将样本公司以“利息支出/固定资产净额”的中位数为临界值分为两组:高、低融资约束组。对两组制造业企业融资约束(FC)不存在门槛值、存在一个门槛值以及存在两个门槛值分别进行估计,验证结果见表10。

表10 面板门槛效应验证结果
由表10可知,高、低融资约束企业以融资约束为门槛变量,模型中均存在两个门槛值,均在10%水平以上显著,门槛值估计结果如表11。

表11 门槛值估计结果
根据门槛回归结果,得出高、低融资企业的2个门槛估计值在95%置信区间下的似然比函数图,低融资约束企业的似然比函数图如图3,高融资约束企业似然比函数图如图4。由验证结果知,高、低融资约束企业的门槛值是真实有效的。

图3 低融资约束企业双门槛估计结果

图4 高融资约束企业双门槛估计结果
高、低融资约束企业面板门槛回归结果见表12。

表12 门槛模型参数估计结果
高融资约束企业回归结果。由表12可知,当FC≤0.0001,政府补贴对研发投入回归系数为0.424,在1%水平上显著;当0.0001
低融资约束企业回归结果。由表12知,当FC≤0.0818,政府补贴对研发投入回归系数为0.115,在1%水平上显著;当0.0818
将高、低融资约束企业结合来看,当政府补贴强度处于前两个阶段时,政府补贴对高、低融资企业的研发投入均起到促进作用,但政府补贴对低融资企业研发投入的促进作用小于对高融资企业研发投入的促进作用。这是因为:第一,面临高融资约束的企业可能存在具有开阔前景的研发项目,但由于风险性和信息不对称性使得企业的融资活动受到阻碍,如果政府此时给予的补贴增多,就可提升高融资约束企业的研发投入;第二,政府补贴企业会向市场传递信息,政府补贴的越多,越能代表企业有开展研发项目的潜力,间接向金融机构传递该企业未来可获得较高经济收益的信号,解决企业与金融机构之间的风险性和信息不对称性。因此当政府补贴较低时,企业面临融资约束越高,政府对企业创新研发的激励效果越大,假设2得到验证。
当政府补贴程度高时,政府补贴对高融资约束企业的研发投入起到促进作用,但促进作用明显减弱,表明此时单位政府补贴对研发投入激励效果不是最佳。而政府补贴对低融资约束企业的研发投入回归系数未通过显著性,可能因为低融资约束企业融资困难较低,政府的直接补贴易使企业资金充裕,补贴资金继续涌入不会对研发投入起作用,假设3得到验证。
综上所述,政府对企业采取补贴时应因地制宜。面临融资约束低的企业,当融资约束处于0.0818和0.0990之间时,政府补贴对研发投入的激励效果最佳;面临高融资约束的企业,当融资约束处于0.0001和0.0367之间时,政府补贴对研发投入的激励效果最佳。
4.4 股权结构调节效应
股权集中度在全要素生产率和研发投入之间调节效应的回归分析如表13,模型1为研发投入对企业全要素生产率(ACF)的回归结果,模型2、3用来验证研发投入与全要素生产率(ACF)的调节变量。模型4、5、6,运用LP法计算全要素生产率,是验证股权集中度调节变量的稳健性检验。
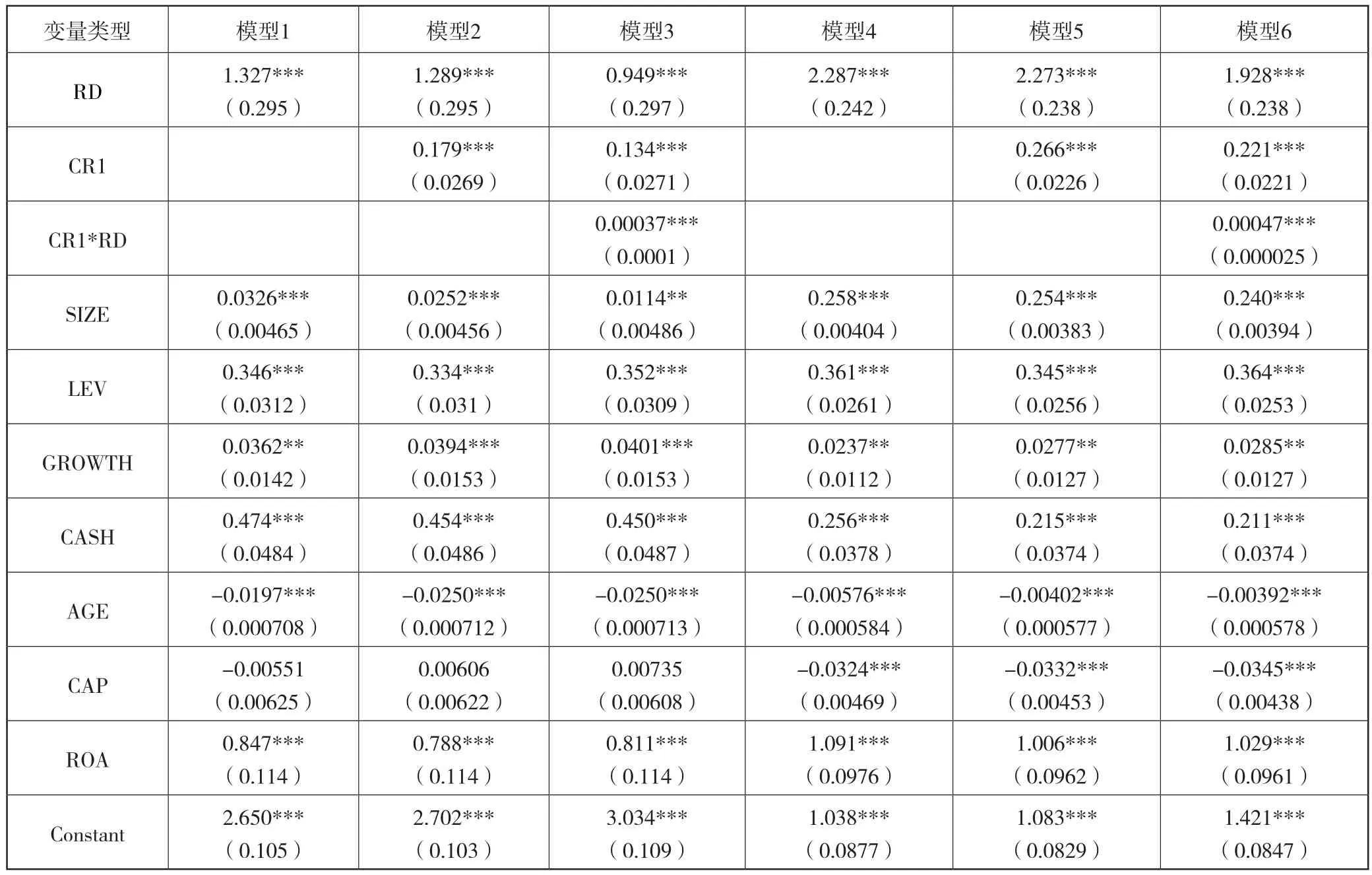
表13 研发投入、股权集中度与全要素生产率的实证分析
研发投入对企业全要素生产率影响回归分析。从回归结果来看,研发投入(RD)正向促进全要素生产率(TFP),系数为1.327,说明样本企业研发投入每增加1%,全要素生产率增加132.7%,在1%水平上显著,表明我国制造业上市公司的研发投入促进企业全要素生产率,验证假设4。
股权集中度调节效应实证结果。模型1为研发投入和全要素生产率的回归结果;模型2加入股权集中度变量,系数为0.179,在1%水平上显著;模型3加入股权集中度和研发投入的交互项CR1*RD,回归系数为0.00037,在1%水平上显著,说明股权集中度在企业全要素生产率与研发投入之间起正向调节作用,验证假设5。
5 结论与启示
如何提升全要素生产率,增强我国技术创新能力,是实施创新驱动发展战略的关键所在。全要素生产率是促进经济增长和提升技术进步的重要指标,全要素生产率的增长主要依靠企业科技进步和生产创新,所以企业应加大研发投入促进其科技进步和生产创新。而制造业企业资本密集度高,面临严重融资约束,所以企业研发活动的开展不仅需要企业自有资金还需要政府补贴的有效调节。本文与以往研究视角不同,以往研究主要专注政府补贴或研发投入对全要素生产率的影响,并未打破政府补贴、研发投入和全要素生产率三者的黑箱。而本文选取2013-2020年制造业上市公司为样本,以政府补贴和融资约束为门槛变量,股权集中度为调节变量,充分考虑OP法和LP法的内生性和不可识别性,运用ACF法准确测量全要素生产率,揭示政府补贴、研发投入与全要素生产率的作用机制,重点分析融资约束的双重门槛效应和股权集中度的调节效应。在现有研究以及理论探索的基础上提出5个研究假设,通过门槛回归和多元线性回归分析进行实证检验,5个假设全部接受。重要结论有五点:第一,政府补贴对企业研发投入具有门槛效应,政府补贴对企业研发投入的促进作用随政府补贴强度的增大而减小。第二,从融资视角看,当政府补贴规模较小时,政府补贴对高、低融资企业均起促进作用,但高融资约束企业促进作用大于低融资约束企业促进作用。第三,当政府补贴强度较高时,政府补贴对高融资约束企业促进作用减小,对低融资约束企业没有影响。第四,研发投入正向促进企业全要素生产率的提高,股权集中度正向调节研发投入和全要素生产率之间的关系。本文首次对政府补贴、研发投入和全要素生产率的关系进行实证研究,在一定程度上弥补有关全要素生产率的实证研究空白。从融资约束的视角,以制造业上市公司为样本研究政府补贴、融资约束和研发投入的非线性关系,研究结果不仅可为政府补贴与研发投入的后续深入研究提供方法指导和理论支撑,同时也对我国制造业企业提升全要素生产率的实践活动具有现实意义。
综上所述,我国制造业企业的政府补贴和全要素生产率具有以下启示:在政府层面,政府补贴倾向于制度层面的引导和激励,而其内涵又涉及到企业多层面,如企业面临的融资约束和知识溢出的外部性,这就需要政府对企业采取补贴时应因地制宜,对面临融资约束程度不同的企业,采取不同的政策,完善补贴分配的评估体系,从而减轻因补贴不当造成的不必要损失,比如“搭便车”、机会主义行为和逆向选择等;在企业层面,不能一味强调分权制衡,分权制衡会降低决策效率,易丧失良机,要重视股权集中度对研发投入和企业全要素生产率之间关系的促进作用,为企业全要素生产率的提升提供更多条件,形成企业独有市场竞争力。
