大数据下基于特征图的深度卷积神经网络
2022-08-09毛伊敏张瑞朋
毛伊敏,张瑞朋,高 波
1.江西理工大学 信息工程学院,江西 赣州 341000
2.中国地质调查局 西安地质调查中心,西安 710000
随着互联网技术的迅速发展以及大数据时代的到来[1],使得大数据相较于传统数据,具有了4V特性[2]——(Value)价值总量高、(Velocity)变化速度快、(Variety)多模态、(Volume)海量,4V特性导致传统分类算法和处理平台很难处理大数据,近年来并行化技术和特征选择型分类算法的发展为大数据处理提供了一个新视角。DCNN[3]是分类算法中的一类重要算法,具有强大的函数逼近能力、特征选择能力以及泛化能力,并被广泛应用于临床医学[4]、地理信息[5]、自动驾驶[6]、语义分割[7]、金融投资[8]、目标检测[9]等领域。因此,基于大数据的并行DCNN研究已经成为目前分类算法的研究热点。
近年来,虽然DCNN在大数据分类领域取得了许多重要成果,但是如何降低网络训练的计算代价仍然是一个重要问题。为了获得性能更加优秀的网络,研究人员不断加深网络的深度和参数数量,如AlexNet[10]、VGG[11]、ResNet[12]和Inception系列[13]等。其中,AlexNet有6 100万个参数,VGG-16参数为1.38亿个,它们分类一个图像分别需要7.2亿和150亿次浮点运算,海量运算带来的时间成本和硬件资源问题十分严峻,而这些问题产生的原因在于DCNN中含有冗余参数。参数剪枝是减少冗余参数的有效方法,它不仅易于平衡压缩速率和性能损失,还具有防止过拟合的潜力,因此受到了广泛关注。Frederick等人[14]提出了基于脑损伤优化的参数剪枝算法,通过计算参数代价函数的二阶导数,去除重要性较小的参数,然而该方法计算成本很高,因此在如今的大型网络上实施该算法是不可行的。因此,Lin等人[15]利用神经元重要性分数来修剪网络,从而减少反向传播误差对剪枝性能的影响,然而该算法剪枝效率较低。综上所述,如何设计合理且有效的冗余参数剪枝策略仍是DCNN界的热点问题。
虽然减少冗余参数能在一定程度上降低DCNN训练的计算代价,但参数的寻优效率对DCNN训练的影响也不容忽视,由于在大数据环境下卷积神经网络收敛速度较慢且易陷入局部最优,因此有学者提出使用群智能算法优化DCNN,提高DCNN寻优效率。Anaraki等人[16]提出了基于遗传算法的卷积神经网络训练方法,避免了BP(back propagation algorithm)算法易陷入局部最优的缺点,但该算法收敛较慢,不适用于大数据环境。因此,Banharnsakun等人[17]利用人工蜂群和有限记忆优化算法共同训练DCNN,该方法在一定程度上提高了DCNN的寻优效率,此外,Gilbert等人[18]通过将DCNN的内部参数空间划分为多个分区,并分别对这些分区进行优化,虽然该策略能显著提高DCNN分类性能,但鲁棒性不强,如果分区大小选择不当,甚至会导致分类性能降低。因此,如何提高寻优效率是当前DCNN训练的重要问题之一。
在大数据环境下影响并行DCNN算法训练效率的因素不只是寻优算法,并行模型的性能也至关重要。近年来研究人员提出了许多大数据处理方法可以有效提高算法效率,其中Google开发的MapReduce并行模型[19]由于其操作简单、自动容错、负载均衡、扩展性强等优点深受广大学者和企业的青睐。目前许多基于Map-Reduce计算模型的神经网络算法已成功应用到大数据的分析与处理领域中。张任其等人[20]提出了CNN-PSMR(parallel strategy of convolutional neural network based MapReduce)算法,该算法采用数据并行的策略,并结合标准与累积误差逆传播算法,提高了网络训练效率。此外,Basit等人[21]提出了DCNN的并行算法MR-DLHR(MapReduce-based deep learning with handwritten digit Recognition case study),提高了DCNN的分类精度,但训练效率仍有不足。因此,Zeng等人[22]提出了SRP-CNN(super-resolution parallel convolutional neural network)算法,该算法引入了反滤波层,并通过多对多连接和并行多态本地网络,进一步提高了DCNN的并行训练效率,但该算法易陷入局部最优解。为了提高DCNN的全局寻优能力,Banharnsakun等人[23]提出了DCNN-PABC(deep convolutional neural network based parallel artificial bee colony algorithm)算法,结合人工蜂群算法和并行化思想寻找最优参数,每个节点使用不同的随机种子来生成初始解,有助于提高搜索空间中解的多样性,加强了算法的全局寻优能力,然而该算法的并行策略没有考虑集群的负载均衡,资源利用率较低,导致并行效率低下。因此如何实现高效率并行训练DCNN仍是一个亟待解决的问题。
针对以上三个问题,本文的主要工作为:(1)设计了一种基于泰勒损失的特征图剪枝策略“FMPTL”,有效减少了冗余参数,降低了DCNN在大数据环境下的计算代价。(2)在获取局部训练结果阶段,提出了基于信息共享搜索策略“ISS”的萤火虫优化算法“IFAS”初始化DCNN参数,实现初始参数取值的优化,提高网络的收敛速度和全局寻优能力。(3)在获取全局训练结果阶段提出了基于并行计算熵的动态负载均衡策略“DLBPCE”,实现系统资源利用的最大化,从而保证并行系统的并行化性能。
1 算法及相关概念介绍
1.1 深度卷积神经网络
DCNN的基本框架如图1所示,它使用多层卷积、池化提取图像的高级语义特征,训练过程分为正向传播和反向传播两个阶段。

图1 DCNN结构示意图Fig.1 DCNN structure diagram
(1)正向传播阶段。对每层输入的特征图计算过程如下:

其中,*代表卷积操作,yl表示第l个卷积层的输出,x(l-1)为第l层的输入向量,bl为第l层的偏置项,I为输入特征图的集合,wr l为l层第r个卷积核的权值,f(x)代表激活函数。
(2)反向传播阶段。比较网络期望的输出和预测结果来调整权值,其目标函数为:

其中,L(p r)为损失函数,p r为反向传播的输入,λ(w)为正则化函数,w代表网络中的权值。
1.2 萤火虫优化算法
萤火虫优化算法(glowworm swarm optimization,GSO)[24-26]是一种模拟萤火虫信息交流过程的优化算法,其主要步骤如下:
(1)初始化荧光素亮度l0,萤火虫感知半径r0,荧光素挥发因子ρ,荧光素更新率γ,并更新荧光素亮度l i(t)。
(2)计算移动概率,选择感知范围内荧光素亮度比自己高的萤火虫作为邻域集,并根据公式(3)计算i移动向j的概率:

(3)迭代更新萤火虫位置:
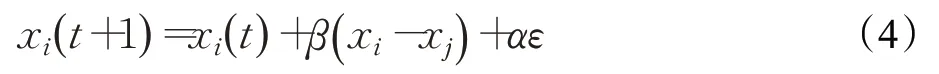
其中,通过萤火虫个体不断移动向感知半径内的较优个体,最终找到问题的最优解。
1.3 并行计算熵
定义1并行计算熵(parallel computing entropy)[27]。若一个并行系统有n个节点,第k个节点的负载为l k,其相对负载率为,则此并行系统的并行计算熵为:

2 MR-FPDCNN算法
2.1 算法思想
MR-FPDCNN算法主要包括三个阶段:模型压缩、局部训练结果的获取和全局训练结果的获取。(1)模型压缩阶段。提出“FMPTL”策略,使用泰勒公式计算特征图的泰勒损失,实现对冗余参数的剪枝,预训练网络,获得压缩后的模型。(2)获取局部训练结果阶段。首先结合MapReduce并行模型,使用Split函数将整个数据集分成大小相同的文件块,存储在每个节点上;接着使用Map函数并行训练每个节点上的网络,提出基于信息共享搜索策略“ISS”的萤火虫优化算法“IFAS”进行参数初始化,提高网络收敛速度和在任务节点上的全局寻优能力,获得局部训练结果。(3)在获取全局训练结果阶段。提出“DLBPCE”策略,提高集群效率,接着使用Reduce函数求出各个节点上DCNN的最终权值,获得全局训练结果。
2.2 模型压缩
目前DCNN模型趋向于深度化的特点使其参数数量呈几何倍数增长,这导致在大数据环境下DCNN对计算机硬件资源的需求急剧增加,不利于其在硬件资源较低的设备上运行。针对这一问题,提出“FMPTL”策略压缩DCNN模型,避免冗余参数过多,导致计算开销过大的问题。“FMPTL”策略如下:
首先,根据图1所示DCNN基本框架进行预训练,公式(2)中的损失函数L使用softmax交叉熵损失,表示N个样本的训练损失:

其中,s n表示第n个样本的softmax函数的输出,t n∈{1 ,2,…,C}表示分配给第n个样本的类标签。
其次,在交叉熵损失的基础上,将第n个样本的特征图x n∈RHW×1损失L使用泰勒公式:

二阶展开,提出线性损失函数“LLF”(linear loss function),以计算去除特征图后分类损失的变化程度。
定义2线性损失函数LLF。若x n表示第n个样本的特征图,δ=-x n,L(x n)表示交叉熵损失,梯度向量,则其线性损失函数“LLF”如下所示:

其中,Hessian矩阵在迭代过程中难以计算,故将其近似表示为H n≈∇n∇Tn。
证明设L为样本的训练损失,x表示特征图,H为Hessian矩阵,p m表示x对m类样本的softmax后验概率。则:

证毕。
接着,由公式(9)可知,当特征图x n的值为零时,δ+x n=0,因此,通过消除零特征图,可以利用公式(9)直接得到基于特征图的泰勒损失公式:

2.3 局部训练结果的获取
在模型压缩之后,使用MapReduce并行训练DCNN,其中,局部训练结果的获取包括Split阶段和Map阶段,在Split阶段,使用Hadoop默认的文件块策略,划分原始数据集成为大小相同的Block;在Map阶段,每个任务节点都存储一个完整的DCNN网络,并调用Map()函数,并行计算DCNN的权值改变量,更新权值,获得局部训练结果。由于DCNN使用反向传播策略更新权值,因此在大数据环境下参数寻优能力不佳,针对这一问题,提出基于信息共享搜索策略“ISS”的“IFAS”算法初始化权值,加快网络收敛速度和在节点内部寻找全局最优解的能力。其具体步骤如下:
首先,在FA算法的萤火虫群的搜索策略中,提出信息共享搜索策略“ISS”,在公式(4)中引入个体适应度和全体适应度的比值,使萤火虫根据公式(11)迭代更新位置时,能够跳出局部最优,提高算法的全局搜索能力,避免陷入局部最优解。信息共享搜索策略“ISS”定义如下:
定义3信息共享策略ISS。若x i(t)为第t次迭代时萤火虫i的位置,s为步长,xmax(t)为萤火虫i感知范围内荧光素值最高的个体,pi为萤火虫i从最优个体学习到的目标信息,则搜索策略“ISS”如下所示:
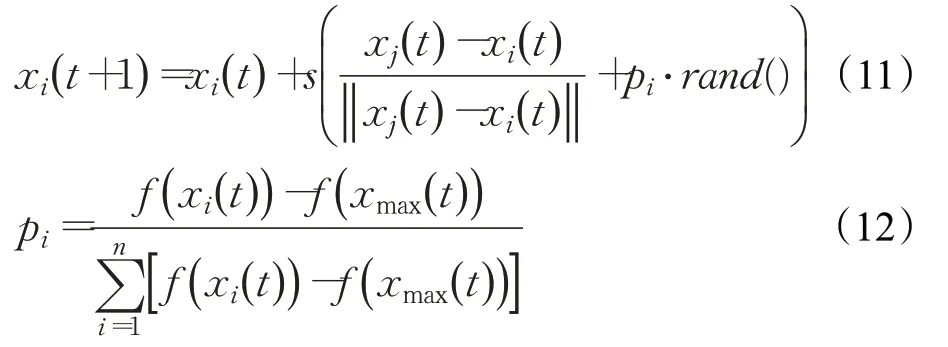
其中,rand()为服从正态分布的随机实数,f(x i(t))-f(xmax(t))为萤火虫i与全局最优个体的适应度之差,为全部萤火虫与最优个体的适应度差值总和。
证明因为f(x i(t))-f(xmax(t))为萤火虫i与全局最优个体的适应度之差,为全部萤火虫与最优个体的适应度偏离总和,若萤火虫i与最优个体适应度差值越大,其他萤火虫个体与最优个体适应度差值总和越小时,则萤火虫i陷入局部最优解,导致pi增大,从而加强对萤火虫i搜索方向的影响,使萤火虫i跳出局部最优,提高其全局搜索能力。证毕。
其次,使用“IFAS”算法初始化参数,并调用Map()函数接收<key=类标号,value=样本值>键值对。
最后,经过正向传播和反向传播计算出每个节点中深度卷积神经网络权值的局部改变量,并将其以<key=w,value=Δw>键值对的形式存入分布式文件系统(Hadoop distributed file system,HDFS)。
2.4 全局训练结果的获取
各个节点经过训练得到DCNN的局部权值,MapReduce将每个Map节点输出的键值对<key=w,value=Δw>传送给reduce()函数完成最终合并任务得到最终网络权值,其中w为权值,Δw表示权值改变量。由于大数据环境下任务量过大,并行系统难以快速地将负载平均分配给每个节点,导致集群响应时间较长,吞吐率较低,针对这一问题,提出“DLBPCE”策略,提高集群资源利用率。“DLBPCE”策略的描述如下:
(1)统计每个任务节点的计算量,将所有任务节点分成轻载、最优、超载三种状态。
(2)对于当前集群,提出动态负载阈值公式“DLTF”(dynamic load threshold function),以控制并行系统到负载均值的距离,从而使集群达到负载均衡。
定义4动态负载阈值公式DLTF。若任务节点的动态负载阈值c∈[csub,ctop],csub和ctop分别为节点动态负载阈值的下限和上限,为集群中所有任务节点负载的平均值,Lmax(t)和Lmin(t)分别为t时刻任务节点中最大和最小的负载量,则动态负载阈值公式“DLTF”为:


其中,η表示动态负载阈值到负载均值的距离。
证明因为和为节点动态负载阈值的上限与下限为动态负载阈值到负载均值的距离,所以,随着任务节点的最大和最小负载量差值减小,动态负载阈值的取值范围也减小,从而使节点负载更加接近负载均值,当集群的并行计算熵大于或等于阈值H b时,并行系统达到负载均衡。证毕。
(3)根据动态负载阈值将任务节点分为三组:
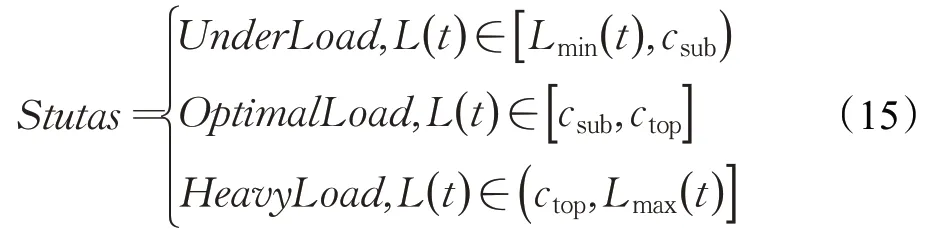
其中,当任务节点负载L(t)∈[Lmin(t),csub]时,该节点处于轻载状态;当任务节点负载L(t)∈[csub,ctop]时,该节点处于最优状态;当任务节点负载L(t)∈[ctop,Lmax(t)]时,该节点处于超载状态。将轻载节点按负载量从小到大排序,并将其放入队列Qlight中;将超载节点按负载量从大到小排序,并放入队列Qover中。
(4)从队列Qover中取出队首节点,将其未处理任务发送给管理节点,管理节点将该任务重新分配给Qlight中的队首节点,若Qover或Qlight的队首节点达到动态负载阈值c,将其出队;若Qlight的队首节点接受新任务后超载,则拒绝该任务,将任务返回给管理节点,并出队Qlight的队首节点,重复该过程,直至其中一个队列为空。
(5)根据公式(5)计算集群的并行计算熵,与预设阈值Hb进行比较,当计算得到的并行计算熵大于等于阈值Hb时,并行系统达到负载均衡,算法结束,调用Reduce()函数合并DCNN的局部权值,得到全局训练结果;反之,并行系统负载不均衡,迭代进行“DLBPCE”策略。
2.5 MR-FPDCNN算法步骤
MR-FPDCNN算法的具体实现步骤如下所示:
步骤1输入原始数据,并通将其划分成大小相同的文件块Block。
步骤2基于原始DCNN模型,调用“FMPTL”策略计算每个特征图的分类损失,并对其进行剪枝,获得压缩后的DCNN模型,将其存入每个任务节点。
步骤3根据“IFAS”算法初始化DCNN权值,并调用Map()函数,在每个节点上经过DCNN的正向和反向传播,生成局部训练结果,并将其存入HDFS。
步骤4根据“DLBPCE”策略控制并行系统的任务节点负载,并调用Reduce()函数合并权值,获得全局训练结果。
2.6 时间复杂度
MR-FPDCNN算法的时间复杂度主要由压缩网络、局部训练结果的获取、全局训练结果的获取这几个步骤构成。网络压缩阶段时间花销为特征图排序与特征图剪枝时间之和,假设预训练样本数为m,特征图剪枝数量为P;在初始化权值阶段,假设Map节点数为a,“IFAS”算法的每一次迭代都要做一次矩阵向量乘法和一些向量内积的计算;在网络并行化训练阶段,其时间复杂度主要取决于卷积神经网络内部的运算,假设网络包含D个卷积层,Cl表示第l个卷积层的卷积核个数,M为每个卷积核输出特征图的边长,K表示每个卷积核的边长;在全局训练结果的获取阶段主要是平衡节点间的负载和权值合并,假设Reduce节点数为r,权值总数为w,“DLBPCE”策略的迭代次数为e,因此MRFPDCNN算法时间复杂度为:TMR-FPDCNN=O(mlgm+
3 实验结果以及分析
3.1 实验环境
为了验证MR-FPDCNN算法训练DCNN的性能,本文设计了相关实验。实验硬件包含1个管理节点,7个任务节点,所有节点的CPU都为AMD Ryzen 9,内存为16 GB,拥有8个处理单元,GPU为NVIDIA RTX2080Ti 8 GB,通过1 Gb/s以太网相连。在软件方面,每个节点安装的操作系统为Ubuntu 20.04,MapReduce架构为Apache Hadoop 3.2.1,软件编程环境为java JDK 1.8.0。节点具体配置情况如表1所示。

表1 各节点的基本配置Table 1 Basic node configuration
3.2 实验数据
本文使用的实验数据为三个真实数据集,它们源于Google Data、Imagenet官网和Mnist,分别为SVHN、ISLVRC2012、Emnist_Digits。SVHN数据集是现实世界拍摄的彩色数字图像,像素为32×32,训练集中有73 200张图像,测试集中有26 000张图像,将其像素标准化至[0,1]的范围内;从ISLVRC2012数据集随机选取500个类别,其中训练图像612 327张,测试图像500 000张,将数据集中的图片像素标准化为224×224;Emnist_Digits数据集是手写字体的黑白图像,32×32像素,训练集240 000张图片,测试集40 000张图片。所有数据集的具体信息如表2所示。

表2 实验数据集Table 2 Experimental data set
3.3 评价指标
本文使用加速比(Speedup)作为指标来评价算法性能。算法的加速比是指通过并行化得到的性能提升,加速比越大,算法的并行化程度越好。其定义为:
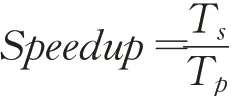
其中,T s表示算法串行执行的时间,T p表示算法并行执行的时间。
3.4 算法加速比的比较分析
为验证MR-FPDCNN算法的并行化性能,本文基于SVHN、Emnist_Digits、ISLVRC2012三个数据集进行实验,根据实验结果的加速比,分别与CNN-PSMR[20]、MR-DLHR[21]、SRP-CNN[22]和DCNN-PABC[23]的并行化性能进行比较分析。实验结果如图2所示。

图2 各算法在三个数据集上的加速比Fig.2 Speedup of each algorithm on three datasets
从图2可以看出,MR-FPDCNN算法在处理大数据集时并行性能较好。在小规模数据集中,如图2(a)所示,当节点数为2个时,MR-FPDCNN算法加速比约为1.6,分别比MR-DLHR和DCNN-PABC算法低0.2和0.1,比CNN-PSMR、SRP-CNN算法高0.4和0.2,但随着计算节点数的增加到6个,MR-FPDCNN算法的加速比超越了MR-DLHR和DCNN-PABC算法,分别比MR-DLHR和CNN-PSMR算法高2.1、1.6、3.3和4.0,这是由于节点数较少时,MR-FPDCNN算法在集群运行、任务调度、节点存储等环节产生了时间开销,而该时间开销在节点较少时,占算法总时间开销的比重较大,因此在MR-FPDCNN算法在这种情况下的加速比较低,而随着节点数的增加,MR-FPDCNN算法的“DLBPCE”策略有效地控制了节点之间的负载均衡,有效利用了集群的资源,因此MR-FPDCNN算法的加速比超越了MR-DLHR和DCNN-PABC算法;在较大的数据集中,CNN-PSMR算法、DCNN-PABC算法、SRP-CNN算法和MR-DLHR算法如图2(b)、(c)所示,4个对比算法的加速比最终趋于稳定,分别为2.7、3.9、6.1和6.8,而MR-FPDCNN算法的加速比随着节点数增加呈线性增长,当节点数为8个时加速比达到9.3,远高于MR-DLHR、DCNN-PABC、SRP-CNN和CNN-PSMR算法,这是由于MR-FPDCNN算法使用“DLBPCE”负载均衡策略,均匀地将分类结果分配到各个计算节点中,算法并行化计算分类结果和更新权值的优点被逐渐放大,使其算法在计算节点增加的同时,加速比呈线性增长,算法的并行化性能得到很大的提升。这也表明MR-FPDCNN算法适用于处理较大规模的数据集,并且随着计算节点的增长,并行化的效果更佳。
4 结语
为弥补传统DCNN算法在大数据环境下的难以训练的缺陷,本文提出了一种新的DCNN训练方法MR-FPDCNN。首先,随机选取部分数据进行预训练,并设计了基于泰勒损失的特征图剪枝策略“FMPTL”,通过比较特征图的泰勒损失实现冗余参数剪枝,从而降低算法计算代价;其次,使用MapReduce对DCNN进行并行训练,并在Map阶段的参数初始化过程中提出了基于信息共享策略“ISS”的萤火虫优化算法“IFAS”,加速了网络训练并提高了DCNN的全局寻优能力;最后,在Reduce阶段提出了基于并行计算熵的负载均衡策略“DLBPCE”,解决了集群资源利用率低的问题,提高了集群的并行化性能。为了验证MR-FPDCNN算法的并行化性能,本文在SVHN、Emnist_Digits、ISLVRC2012三个数据集上对MR-FPDCNN、MR-DLHR、DCNN-PABC、SRP-CNN和CNN-PSMR五种算法进行对比分析,实验结果表明,在大数据环境下MR-FPDCNN算法的加速比明显高于其他几种算法。
