相位转移熵在再认记忆脑网络中的应用研究
2022-08-09齐云鹏王苏弘陈芋圻
齐云鹏,王苏弘,陈芋圻,邹 凌
1.常州大学 计算机与人工智能学院 阿里云大数据学院,江苏 常州 213164
2.苏州大学附属第三医院 临床心理科,江苏 常州 213003
3.常州大学 微电子与控制工程学院,江苏 常州 213164
再认记忆是人类的一项基本认知功能,认知心理学界已使用多种方法对再认记忆进行研究,包括对单词、物体、图片等的再认[1-2]。已有的研究表明,部分病症会影响再认记忆,比较典型的有阿兹海默症、脑梗塞、颅脑损伤[3-4]等。但这些研究均使用ERP来分析再认记忆差异,并未从脑网络方面进行研究。此外,当前对再认记忆的研究大多局限于病症[3-4]这类对大脑有物理性损伤的人群,张毅力等人[2]研究了跨国文化背景对再认记忆的影响,但这一研究只使用了事件相关电位(event-related potential,ERP)和行为学数据,且受到到语言、三观、智力水平等多种因素影响,得到的结果比较宽泛。目前,正常人群因专业教育背景不同而获得不同的先验记忆(如:中国医学生与非医学生)是否会影响之后的再认记忆(简称:后认记忆),经检索尚未发现与之相关的文献。这是再认记忆领域目前的空缺,填补这一空缺将有助于更深入地了解再认记忆的机制,为再认记忆研究丰富理论依据。
脑网络理论已被广泛应用于研究脑功能。根据这一理论,大脑的复杂功能是脑网络中不同区域之间连接的结果。已有的研究表明,大脑的功能和结构网络可以表示为一个复杂的网络模型[5]。迄今为止已有一些研究通过计算各路脑电信号间的相关性,建立大脑功能性网络,再运用复杂网络的理论和方法,分析大脑的网络连接。Supriya等人[6]通过lucasa可见图算法建立了大脑连接网络,并引入了复杂网络统计特性检测不同边缘强度的癫痫脑电信号。Gao等人[7]根据不同节点的EEG信号之间的相对小波熵建立大脑复杂网络,提取了一系列的网络统计量来表征大脑网络的拓扑结构,进行基于脑电图的疲劳驾驶分类。
在记忆与脑网络结合这一领域,目前已经有研究用构建脑网络的方法对记忆相关领域进行探索,但这些研究仅将脑网络作为一种量化指标[8],用以评估提出方法的有效性,并未从脑网络的角度深入分析。这也是目前再认记忆研究的不足之处。大脑是一个复杂的系统,使用脑网络的方法对再认记忆进行分析有助于更深入、更详细地了解再认记忆。
大脑区域间的信息流动,本质上是信息从一个区域传播到另一个区域的过程,这一动态过程可以使用复杂网络的信息传播过程进行描述[9-11]。在基于EEG数据构建的复杂脑网络中,将电极作为网络节点,电极之间的连通性作为边,若边为加权有向边,则可以将其视为节点之间有向的、量化的信息传播。一个经典的有向连接度量是基于信息论的转移熵(transfer entropy,TE),TE是一种无模型连接度量,它显示交互的方向并包含线性和非线性耦合。Lobier等人[12]将TE在相位数据上扩展为相位转移熵(phase transfer entropy,PTE),它具有TE的优点以及对噪声和线性混合更强的鲁棒性,并且只需要较少的数据和计算时间就可以反映信号的耦合关系,基于此度量构建的网络将包含有关大脑区域相互作用的更全面的信息。目前该方法已被应用于脑磁图[13]和心电信号[14]的功能连接分析。但PTE在脑电领域的应用不多,Wang等人[15]使用PTE对癫痫病人的立体脑电图(stereo-electroencephalography,SEEG)数据进行分析,成功预测了颞叶癫痫的致痫区。Hasanzadeh等人[16]基于重度抑郁症患者和正常受试者的EEG数据,使用PTE构建脑网络,并结合图论指标评估网络特征的差异,之后又对两组受试者进行分类,得到92%的分类准确率,证明PTE是一种基于EEG数据构建脑网络的有效方法。
由于目前对不同先验记忆影响后认记忆这一方向的研究存在空缺,并且对再认记忆的研究大多是从ERP和行为学数据两方面进行分析,尚未从脑网络方面对再认记忆深入研究,又考虑到受试者都是正常人群,两者之间的脑网络差异可能不会很明显,使用无向连接无法体现出两者之间的差异,因此本文采用相位转移熵方法构建有向加权再认记忆脑功能网络,以医学生和非医学生为受试者,探究不同的先验记忆对后认记忆的影响,并结合复杂网络的理论和方法,按照“复杂网络特征-关键网络节点-主要脑区”的思路,从复杂网络特征、网络枢纽、有向差分连通图(directed differential connectivity graph,dDCG)三个方面深入分析再认记忆在大脑网络特征上的差异。本文丰富了再认记忆领域的研究,为再认记忆的研究提供一种新的思路,也为再认记忆的脑网络研究提供支持。
1 数据采集与预处理
1.1 受试者信息
在苏州大学医学院募集被试,采用单双数法随机选取中国医学生36名(男性19名,女性17名),年龄21~22岁,平均年龄(21.90±0.73)岁;在苏州大学募集被试,采用单双数法随机选取中国非医学生37名(男性19名,女性18名),年龄21~23岁,平均年龄(21.72±1.42)岁,两组受试者之间年龄差异无统计学意义(P>0.05)。所有受试者均为五年制临床医学专业四年级,右利手,视力或矫正视力正常,无精神及神经系统疾病,无药物滥用,研究已通过苏州大学附属第三医院伦理委员会批准,实验前获得受试者本人书面知情同意。
1.2 实验范式
从医学图片库和非医学图片库中各随机抽取图片120张。采用国际通用的再认记忆模式,分为两个结构相同的组块,每个组块包括医学、非医学图片各60张,两个组块无重复图片,中间休息2 min。组块结构:(1)学习阶段。黑屏白背景刺激图片位于液晶屏中央,大小为8 cm×8 cm,共呈现60张图片,医学图片和非医学图片各30张,每张图片显示2 000 ms,间隔1 000 ms;要求被试者记忆呈现图片。(2)再认阶段(区分旧图及新图过程)。学习阶段出现过的图片(学习过的)称为旧图,未出现(未学习过)的图片为新图。每张图片显示2 000 ms,间隔1 500~2 000 ms,共伪随机呈现120张图片,新图和旧图各60张,要求被试者判别看到的图片是新图还是旧图。学习阶段与再认阶段间隔1 min。
1.3 数据预处理
所有数据均使用美国EGI脑电图系统采集,电极的位置依照国际10-20标准,采样率为500 Hz。使用EEGLAB工具箱对所采集的脑电数据进行预处理,得到去除大部分噪声后的脑电数据,步骤包括:(1)滤波:范围为0.1~45 Hz。(2)伪迹检测(astifact detection)。采用主成分分析(PCA)法,去除眨眼和眼动伪迹;(3)坏导替换(bad channel replacement)。(4)参考点转换(montage operations)。采用平均参考;(5)分段(segment)。分段范围为-200~1 000 ms。(6)基线校正(remove baseline)。范围为-200~0 ms。
2 实验方法
2.1 相位转移熵构建脑网络
构建大脑网络的第一步是选择节点和计算连接强度(即边)。在本研究中,每个电极被认为是一个节点,共128个节点。引入PTE这一连通性度量,用于确定图的边缘。PTE是应用于信号相位时间序列的转移熵。转移熵表示一个过程过去的信息量,可用于在目标过程过去的背景下预测另一个过程的未来。计算PTE的步骤如下:
步骤1获取EEG信号的相位数据。信号的瞬时相位可以从该信号的分析形式中获得。对于信号X(t),为了获得瞬时相位时间序列θ(t),将解析信号定义为:

其中,A(t)是信号的瞬时幅度,S(t)通过对X(t)进行复滤波(如Morlet小波变换或Hilbert变换)获得。本文使用Hilbert变换。之前的研究结果表明,如果信号是窄频带,则可以适当地定义信号的瞬时相位,因此将带通滤波设置为delta(1~3 Hz)、theta(4~7 Hz)、alpha1(8~10 Hz)、alpha2(10~12 Hz)、beta1(13~16 Hz)、beta2(16~20 Hz)、beta3(20~25 Hz)和beta4(25~30 Hz)8个子频带[14],从每个子频带的128通道EEG数据中提取瞬时相位。
步骤2计算边际熵和联合熵项。熵的定义为:

其中,t′=t-δ,δ表示分析时滞,θy(t′)、θx(t′)表示瞬时相位在过去时间点t′时的状态。H(θ)表示香农熵。计算方程式(2)~(5)中的概率,需要估计有限时间序列背后的过程的状态空间。
本文使用相空间分箱和实验折叠相结合的方法,对于每个概率密度函数,通过对所有实验中单个、成对或三元组相位数据点的出现进行适当分箱,构建了一个基于直方图的概率函数。定义每个箱的宽度其中h j表示相位时间序列θ(j)的箱宽度(j=y(t),y(t′)或x(t′)),N是样本数,σj是方向变量的标准偏差,由Fisher定义。因此,对于θy(t)、θy(t′)和θx(t′),箱的数量为:k(j)=2π/h(j)。最后,通过将每个箱中的数据点数除以数据点总数来计算每个箱的概率值。
步骤3计算PTE。信号的PTE定义为:

将步骤2中得到的熵根据公式(6)进行计算,即可得到两个节点之间的PTE。对每对节点之间的PTE进行计算,共需计算128×127次。
步骤4确定连接方向。定义X到Y之间的定向连接为dPTE:

若d PTE x->y>0,则连接方向为X到Y,反之则方向为Y到X。最终得到8 128条有向边。
2.2 复杂网络特征
在网络构建之后,使用复杂网络特征以评估网络的特性。基于复杂网络理论的大脑连接网络图中具有很多有价值的网络特征,提取这些复杂网络特征参数可以有效反映大脑网络的状态。本文所计算的复杂网络特征如表1所示。网络特征由大脑连接工具箱(brain connectivity toolbox)计算。

表1 应用图论指标的简要描述Table 1 Brief description of applied graph theory metrics
为了评估医学生与非医学生的再认记忆脑功能网络的差异,对8个研究频段和两种刺激(旧医学图片和旧非医学图片)进行了医学生与非医学生组之间的统计分析,对每个复杂网络特征进行独立样本T检验进行比较。影响每项测量的因素是两组(MS和OS)和128个EEG电极(节点),本文的研究重点是组差异。
2.3 分析网络枢纽
在网络中,若一个节点的度数比网络的平均度数高出一个标准差以上,则这个节点可以视为网络枢纽。网络枢纽在网络中的信息传递中起着重要作用。根据计算出的节点度和节点强度,使用MATLAB绘制网络枢纽图,并过滤掉节点度和节点强度过小的冗余节点,对比分析网络枢纽之间的差异。
2.4 构建有向差分连通图
分形结构是现实网络中普遍存在的特征,脑网络也具备这一特性[17-19],每个脑区可以看作脑网络的一个大节点,脑区内部构成子网络,结构与整体脑网络相似,多个子网络互相连接、影响就构成了整体的脑网络。每个子网络负责处理不同的任务。这些子网络的状态(如网络密度、子网络间信息交互等)变化导致大脑分形结构的改变,从而影响脑网络的功能。这一步可使用dDCG进行分析。
dDCG由两组之间有显著性差异的连接构成,使用dDCG来表示医学生与非医学生之间边明显不同的网络;在每个频带中构建一组dDCG,对于频带中的每个对象,使用PTE矩阵作为链接值,用独立样本T检验筛选出具有显著性差异的连接,根据筛选结果使用dPTE矩阵构建dDCG,并使用brainstorm工具箱绘制dDCG。
3 结果
3.1 复杂网络特征统计结果
为了评估医学生与非医学生的脑网络差异,对医学生(MS)与非医学生(OS)组的复杂网络特征进行统计测试。表2、表3显示了所有频带中MS和OS组受试者的复杂网络特征的平均值,包括出度(OutDeg)、入度(InDeg)、出入度之比(OD/ID)、出强度(OutStr)、入强度(InStr)、局部效率(LE)、全局效率(GE)和介数中心性(BC),图片刺激包括旧医学图片(mo)和旧非医学图片(oo)。粗体数字代表具有显著性差异(P<0.05)。
从表2、表3可以看出,在节点出入度和BC方面,医学生和非医学生不存在差异。在mo组的theta和beta2频段中,MS组的出入度之比要小于OS组,而在oo组的delta和beta1频段中,MS组的出入度之比大于OS组。对于节点出强度,在delta、theta和alpha频段的mo组中MS组的出强度大于OS组,在beta频段中则相反,而在oo组中,delta、alpha2和beta1频段的MS组的出强度要大于OS组,在beta2、beta3、beta4频段中则相反。对于入强度,mo组在delta和theta频段中MS组的入强度要大于OS组,在beta2、beta3和beta4频段则相反,而在oo组中,beta4频段MS组的入强度小于OS组。对于局部效率,mo组的delta、theta、alpha、beta1频段中MS组的LE大于OS组,在beta2、beta3频段则相反,oo组的alpha2、beta1、beta2频段中MS组的LE大于OS组,在delta、theta、beta4频段中则相反。关于全局效率,mo组的delta、theta频段中MS组的GE大于OS组,beta2、beta3、beta4频段中则相反,而oo组中,仅在beta4频段中MS组的GE小于OS组。
表2 旧医学图片(mo)组医学生和非医学生所有频段的平均网络度量(±s)Table 2 Average network measurement of all frequency for medical and ordinary students in old medical pictures group(mo)(±s)
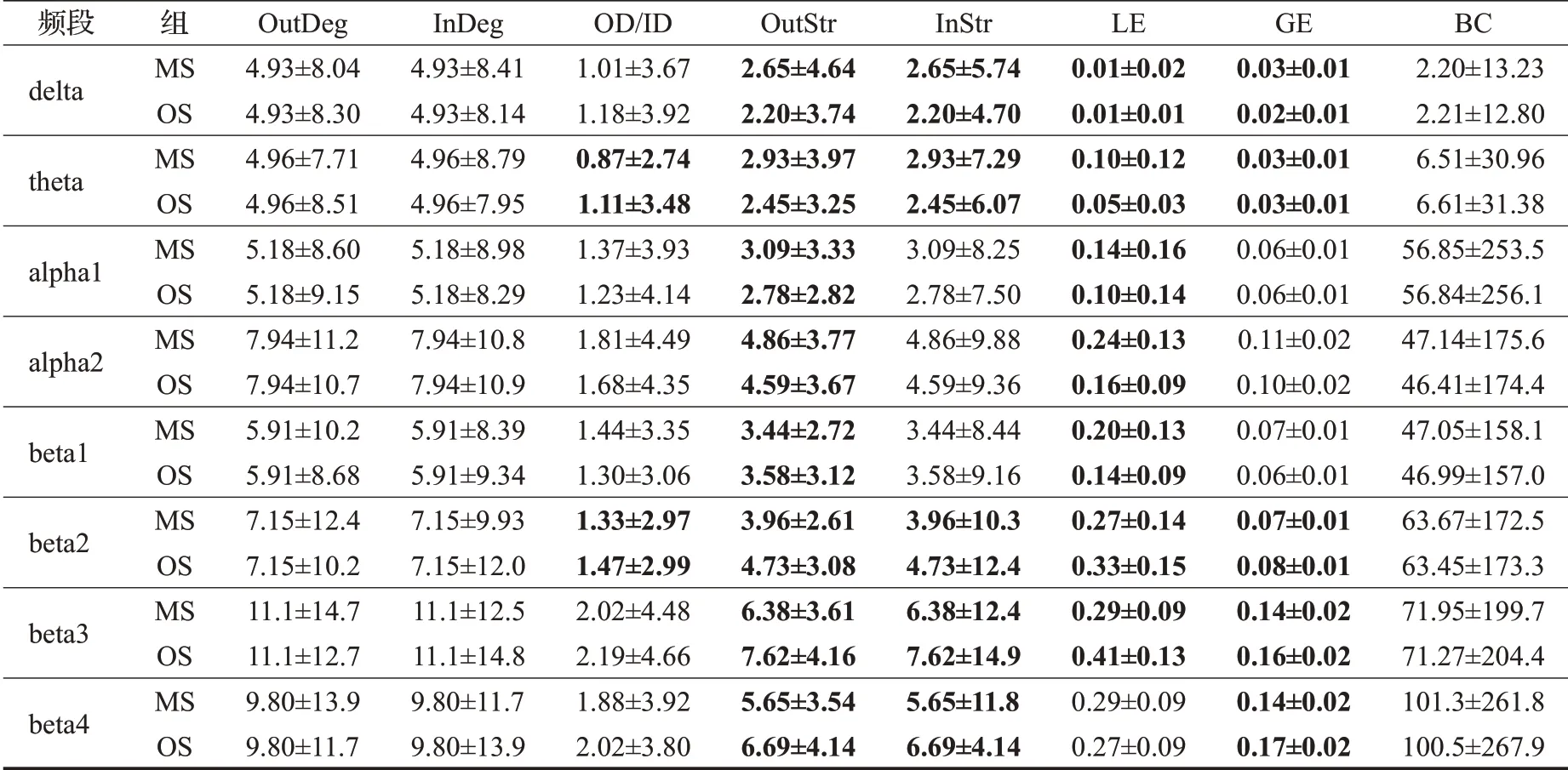
表2 旧医学图片(mo)组医学生和非医学生所有频段的平均网络度量(±s)Table 2 Average network measurement of all frequency for medical and ordinary students in old medical pictures group(mo)(±s)
表3 旧非医学图片组(oo)医学生和非医学生所有频段的平均网络度量(±s)Table 3 Average network measures of all frequency bands for medical and ordinary students in old ordinary pictures group(oo)(±s)
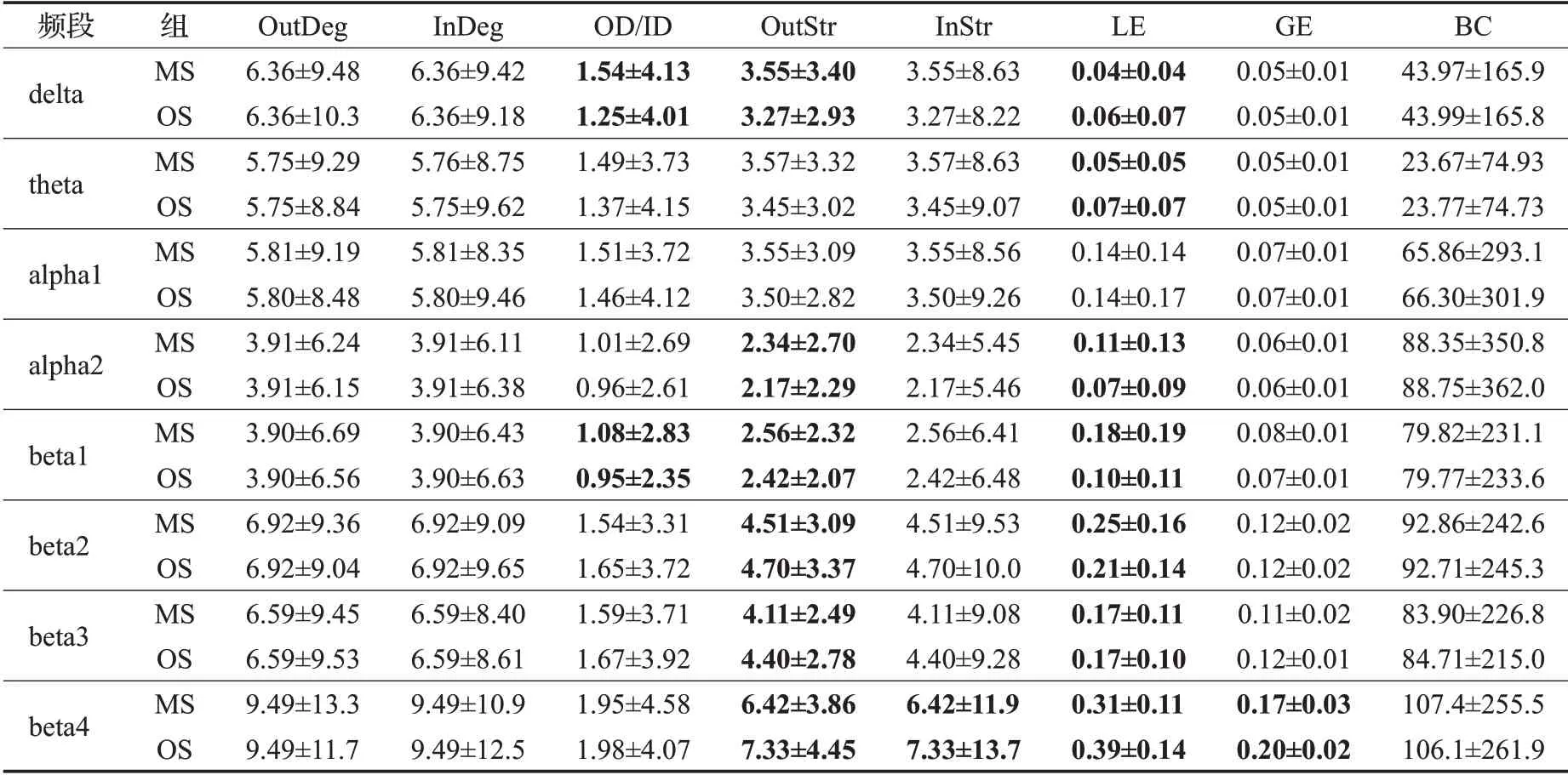
表3 旧非医学图片组(oo)医学生和非医学生所有频段的平均网络度量(±s)Table 3 Average network measures of all frequency bands for medical and ordinary students in old ordinary pictures group(oo)(±s)
综合上述结果可以发现,对于所有具有显著性差异的指标,在beta3(20~25 Hz)和beta4(25~30 Hz)频段中MS组的指标数值均小于OS组。
3.2 网络枢纽对比分析
为了研究图片再认期间医学生与非医学生脑功能网络枢纽的差异,对两组之间的节点度数(节点的出度和入度之和)和节点强度(节点的入强度和出强度之和)进行对比,分析网络连接权重的差异。在提取这些指标时,先对两组数据进行独立样本T检验,仅选择两组之间具有显著性差异的网络连接。图1和图2分别描绘了所有频带中电极的平均节点度和平均节点强度,电极体积代表节点度,电极颜色代表节点强度。同时构建了统计量t:
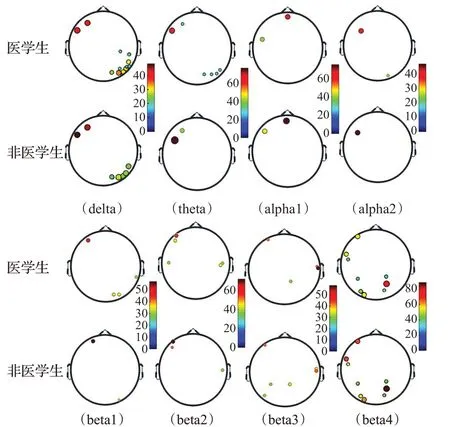
图1 对旧非医学图片进行再认时各个频段的网络枢纽图Fig.1 Network hub diagram of each frequency during recognition of old ordinary images

图2 对旧医学图片进行再认时各个频段的网络枢纽图Fig.2 Network hub diagram of each frequency during recognition of old medical images

其中,deg为度或节点强度,max代表最大值,min代表最小值。由于网络枢纽的度数比网络的平均度数高出一个标准差以上,因此可以过滤掉一些节点度和节点强度过小的电极,让网络枢纽的结果更加简洁清晰。从t=0%开始,以10%为步长设置阈值并绘图,根据每个频段的实际结果,选择不同的阈值(30%~50%)。这样的阈值过滤后不仅会保留网络枢纽,也会保留下一些节点度和节点强度较大但非网络枢纽的节点,会尽可能地保留一些有用的信息,有助于之后的分析。
对图片的再认涉及到视觉、图片识别、判断、短期记忆等,与这些功能相关的大脑区域为枕叶、颞叶和额叶,而再认记忆的“新/旧效应”会出现在顶叶及额叶中部,因此脑功能网络的枢纽应当会位于枕叶、颞叶、顶叶和额叶这四个区域中。
图1显示了医学生和非医学生对旧非医学图片进行再认时各个频段的平均节点度(以电极体积表示)和节点强度(以电极颜色表示)。如图1所示,医学生和非医学生在对旧医学图片进行再认时,脑功能网络的枢纽主要位于枕叶(beta4)、额叶(delta、alpha1、alpha2、beta1、beta2)、左侧颞叶(delta、theta)和右侧颞叶(beta3)。两组的节点度没有明显差异。除beta3频段外,医学生在所有频段中的节点强度(P<0.05)均低于非医学生。
图2显示了医学生和非医学生对旧医学图片进行再认时各个频段的平均节点度(以电极体积表示)和节点强度(以电极颜色表示)。如图2所示,医学生和非医学生在对旧医学图片进行再认时,脑功能网络的枢纽主要位于枕叶(delta、theta、alpha2)、额叶(alpha1、alpha2、beta1、beta2、beta4)和左侧颞叶(beta3)。两组的节点度没有明显差异。在所有频段中,医学生在额叶区域的节点强度(P<0.05)均低于非医学生,而在顶叶和枕叶的节点强度(P<0.05)要高于非医学生。
比较图1和图2的结果,两组受试者的网络枢纽位置相同,医学生在额叶部位的网络枢纽强度均小于非医学生。从再认旧非医学图片到再认旧医学图片的过程中,网络枢纽在delta、theta、alpha1、alpha2、beta3和beta4频段中发生了变化。在delta和theta频段中,网络枢纽从左侧颞叶转移到枕叶。在alpha1频段中,顶叶部位新出现一个网络中枢。在alpha2频段中,在枕叶区域也出现一个网络中枢。在beta3频段中,网络枢纽从右侧颞叶转移至左侧颞叶。在beta4频段中,网络枢纽从枕叶转移至额叶。这表明在对旧非医学图片进行再认时,大脑的主要活跃区域为额叶,在对旧医学图片进行再认时,顶叶、枕叶和颞叶活跃程度提高。
3.3 构建有向差分连通图
选择具有显著性差异的连接,并绘制dDCG。由于具有显著性差异的连接数量较多,且brainstorm绘制的连通图中颜色只代表方向不代表连接强度,因此需要过滤掉一些弱连接,使两者之间的主要差异更加突出。设定阈值区间为0~50%max(N),以10%max(N)为步长逐步过滤,综合所有频段的结果,最终得到30%max(N)为最佳阈值,且delta和theta频段的结果最清晰。以delta频段为例,图3和图4分别为对旧医学图片和旧非医学图片进行再认时,各阈值下的dDCG。

图3 对旧医学图片再认时delta频段各阈值下的dDCGFig.3 dDCG at each threshold of delta frequency during recognition of old medical images
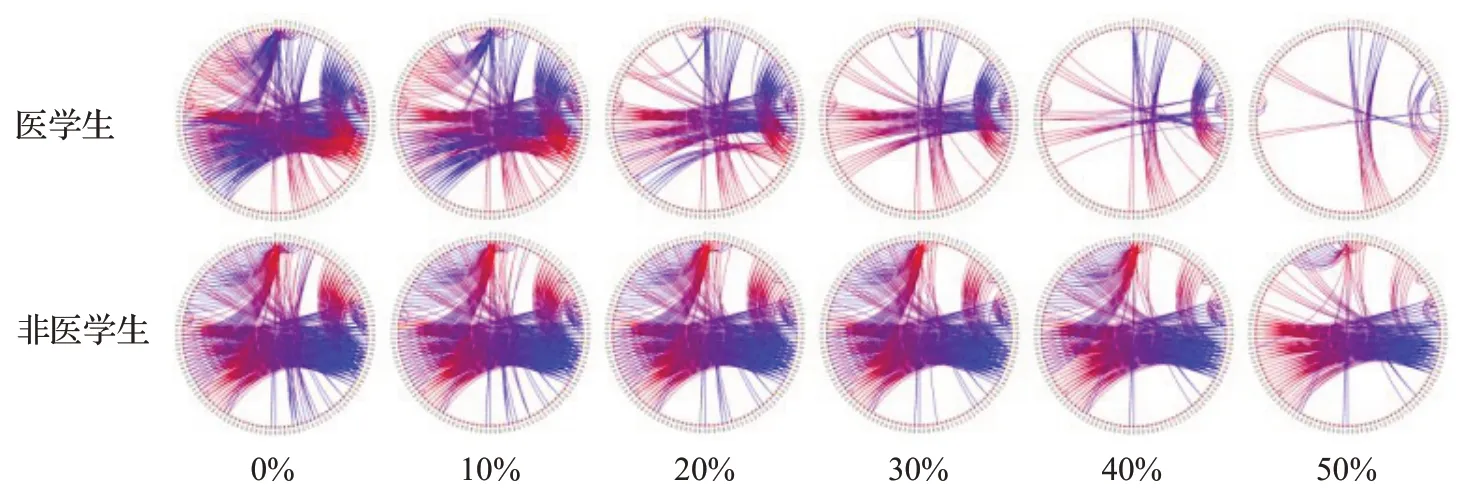
图4 对旧非医学图片再认时delta频段各阈值下的dDCGFig.4 dDCG at each threshold of delta frequency during recognition of old ordinary images
图5和图6分别为医学生和非医学生对旧医学图片和旧非医学图片进行再认时各个频段的dDCG,网络连接方向为由蓝到红。从图5和图6中可以看出,在delta和theta这两个频段中,在对医学图片进行再认时,医学生的脑网络存在从左侧颞叶流向右侧枕叶的信息流,而非医学生则相反;在对非医学图片进行再认时,在delta频段中,医学生有一条从右侧颞叶指向右侧枕叶的信息流,而非医学生则相反。这表明在执行再认任务时,医学生与非医学生激活相同的脑区,但侧重的脑区不同,脑区间的信息交互也不同。
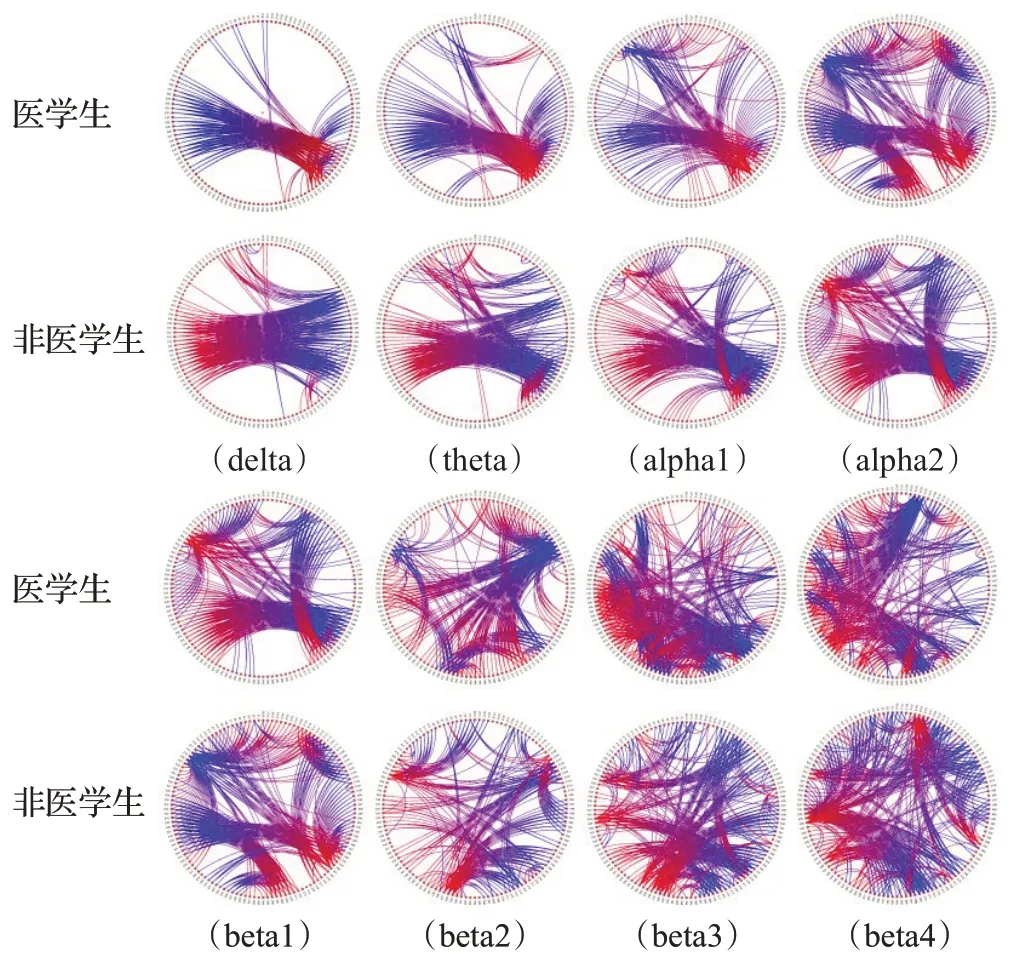
图5 对旧医学图片进行再认时各个频段的dDCGFig.5 dDCG of each during recognition of old medicalimages
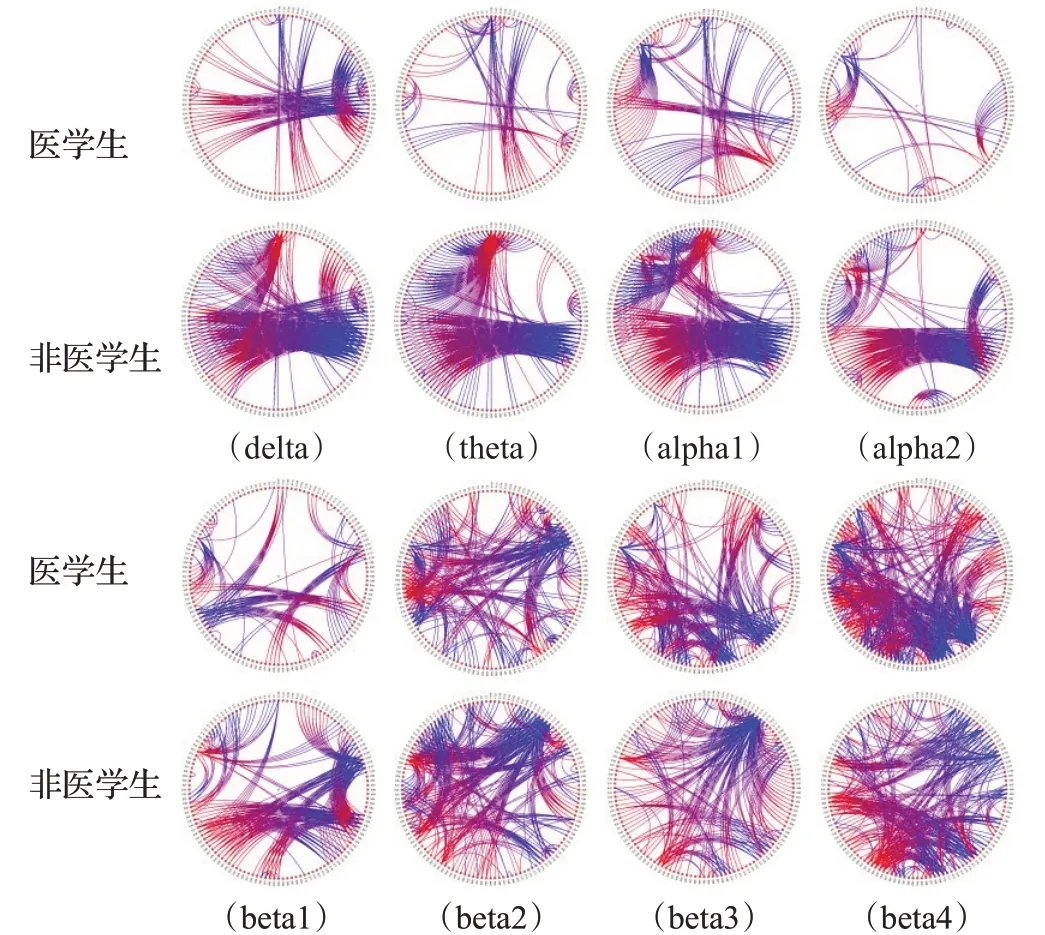
图6 对旧非医学图片进行再认时各个频段的dDCGFig.6 dDCG of each frequency during recognition of old ordinary images
4 讨论
对复杂网络特征的统计结果显示,仅在beta3和beta4频段中MS组与OS组之间的差异具有一致性。在这两个频段下,MS组的平均出强度、入强度、局部效率和全局效率均小于OS组,并且在mo条件下差异更大,表明在进行图片再认任务时,医学生的复杂脑网络节点间的连通性、大脑局部区域内及大脑整体的网络信息传播能力均低于非医学生。而在接受医学图片刺激时,这一差异会进一步放大。
对节点度数的分析表明,医学生和非医学生在对图片进行再认时,网络枢纽的位置相同,两组之间的节点度数不存在显著差异,而节点强度存在差异。并且在对旧医学图片进行再认时,更多的网络枢纽出现在枕叶、顶叶和颞叶区域。
最后,分析了医学生和非医学生的dDCG。dDCG中电极之间的加权有向连接可视为信息流,即复杂脑网络中的有向量化信息传播。结果显示,在对旧医学图片进行再认时,医学生大脑的信息主要从左颞叶传播至右枕叶,而非医学生大脑的信息主要从右颞叶、右枕叶传播至左枕叶、左颞叶,信息传播与接收的区域分布具有对称性,这一特征目前尚未找到相关文献佐证。存在这一差异的原因可能是医学生在过去学习过医学图片,进行再认时要额外进行识别医学图片是否为再认任务中的图片这一步骤,为实现这一功能,脑网络的分形结构发生改变。此外在实验过程中发现,医学生与非医学生在进行再认任务时的信息流主要位于额叶、枕叶、颞叶等数个脑区,与其余脑区间的连接多为弱连接(虚假连接),而这些连接对于试验结果无正面影响。后续可以尝试使用构建相关脑功能区域子网络的方法,探索图片再认任务具有不同先验记忆的脑功能连接差异。
5 总结
本文使用PTE方法构建基于EEG信号的有向脑连接网络,探索不同先验记忆对后认记忆的影响,并以复杂网络特征、网络枢纽以及有向差分连通图三种形式体现了医学生与非医学生之间再认记忆的差异。实验结果说明,PTE是一种计算EEG数据有向脑功能连接的有效方法,该方法可以显示出脑区之间的信息传播,更好地体现出一些不明显的差异,此外也证明了从脑网络角度对再认记忆进行研究的可行性,为该领域的研究提供了一定的理论支持。
