基于蒙特卡洛方法的覆冰导线舞动跳闸概率计算

2022-08-09马增泰罗萍萍孙天杰林济铿

电力科学与技术学报 2022年3期

马增泰，罗萍萍，孙天杰，林济铿，刘辉

(1.上海电力大学电气工程学院，上海 200090；2.同济大学电子与信息工程学院，上海 201804；3.国网安徽省电力有限公司，安徽合肥 230022)

架空导线的舞动是导线覆冰后，在横向风的作用下形成的低频率、大振幅的自激振动，其对电力系统的安全运行构成严重的威胁[1-4]。安徽、浙江、河南等省份在多次遭受冰冻天气时，均出现了覆冰导线舞动导致的大范围线路跳闸等恶性事件[5]。由于架空输电线路的舞动受气象条件影响较大，如何科学合理地根据气象信息来计算架空线路的覆冰舞动跳闸概率，并对跳闸概率大的线路采取预防措施，对于提升电网应对灾害天气的能力，具有非常积极的理论和实际工程意义。

目前对覆冰架空导线舞动的研究主要集中在2个方面：舞动机理与模型的研究和基于线性化思想的舞动跳闸概率研究。舞动机理与模型的研究包括垂直方向舞动机理[6]、扭转方向舞动机理[7]等。覆冰导线的舞动模型主要有单自由度舞动模型、双自由度舞动模型及三自由度舞动模型[8]，并采用包括增量谐波法[9]、矩阵摄动法[10]、有限单元法[11]、牛顿法[12]等方法推导覆冰导线的舞动运动方程。文献[12]使用牛顿法建立了单自由度舞动模型，并使用慢变参数法获得舞动幅值的解析解，然而覆冰导线舞动是大几何非线性运动，慢变参数法只适用于弱非线性运动方程；文献[13]采用有限元的思想，使用索单元来建立覆冰导线的舞动模型，并使用振型叠加法求解该模型，得到了导线舞动的幅值；文献[14]利用D’Alembert原理建立了覆冰导线的单自由度与双自由度舞动模型，算例验证了方法的正确性；文献[15]使用Hamilton原理建立覆冰导线的三自由度舞动模型，并实现了对舞动形态的数值模拟，然而三自由度舞动模型不能得到舞动幅值的解析解。

基于线性化思想的舞动跳闸概率研究，其基本思想是先计算出覆冰导线舞动的幅值，然后与相间距离比较，进而得到以导线舞动幅值为自变量的线性化的跳闸概率。文献[16]提出了一种基于支持向量机(support vector machine,SVM)和自适应增强(adaptive boosting,AdaBoost)分类器的覆冰架空线路舞动跳闸预警方法，通过挖掘易舞动区域的气象数据来构建基于SVM分类器的易舞气象预报模型，从而得到舞动幅值的预测结果以及相应的跳闸概率；文献[17]使用拉力传感器及覆冰导线实时水平荷载估算出导线舞动幅值，然后与导线相间距离比较得到舞动跳闸概率；文献[18]基于现场舞动观测点的温度和湿度的信息对舞动幅值进行实时预测；文献[19]基于拉力与角度传感器所得到的覆冰导线张力与风攻角，推出覆冰导线舞动的幅值，并得到跳闸概率。基于线性化思想的舞动跳闸概率研究不足之处在于仅以舞动幅值与导线相间距离来计算跳闸概率，未考虑两相导线的非同步舞动。

本文提出基于蒙特卡洛方法的导线舞动跳闸概率计算方法。由风速与冻雨量等气象信息，计算导线覆冰厚度并建立风速的Weibull分布函数，然后根据牛顿定律建立覆冰导线单自由度舞动模型；使用Fluent软件对不同冰厚的半椭圆型覆冰导线进行气动力仿真，得到气动系数与覆冰厚度的关系式，进而采用里茨—伽辽金方法求解舞动模型，获得以风速为自变量的舞动幅值解析表达式，并由风速的分布函数获得舞动幅值的概率分布函数；为了解决舞动跳闸数据收集过程的繁琐且效率低下的问题，本文通过分析三相导线发生非同步舞动时的相位关系，得到某一舞动幅值下线路固有的跳闸概率计算模型；最后，使用蒙特卡洛方法模拟覆冰导线舞动跳闸的过程，获得覆冰导线舞动越限跳闸概率的统计值。

1 舞动跳闸故障的概率模型

1.1 舞动幅值的概率模型的建立

导线的舞动是在覆冰的基础上发生的，本文以极端天气下冻雨时间里的风速与冻雨量信息计算导线的覆冰厚度[20]，覆冰厚度为

rice=

(1)

式(1)中的rice为圆形覆冰冰厚，而实际导线的覆冰常是不规则的半椭圆型或新月型。本文结合实际情况[21]，将冰厚为rice的圆形覆冰截面等效为参数为rH、ry的半椭圆形覆冰截面，其中rH为横向增长冰厚，ry为竖向增长冰厚，如图1所示。假设2种覆冰形状的覆冰截面面积相等和半椭圆形覆与冰横竖向覆冰增长成比例，则rH、ry以及rice的关系为

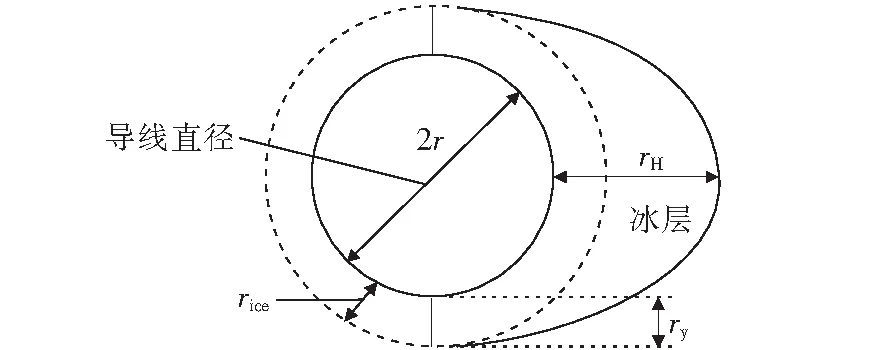
图1 覆冰导线截面Figure 1 Section of iced wire

(2)

式中r为裸导线导线半径。对于新月形覆冰，可将导线ry方向的冰厚与rH方向的冰厚取相等值ra，令ra=2rice。

研究覆冰导线舞动的幅值与稳定性的问题时，常用到单自由度舞动模型，即导线垂直舞动模型。采用多项式拟合覆冰截面的气动系数后，单档覆冰导线的单自由度舞动运动方程[12]可以表示为

(3)

式中m为覆冰导线质量，m=πr2ρL+0.5πρice(rHry-r2)；ζ为阻尼比；ω为覆冰导线体系自振频率；k为覆冰导线体系的刚度；ρair为空气密度；D为覆冰导线直径；y为覆冰导线在垂直方向的位移；c1、c2均为气动参数。

由于覆冰导线舞动是小应变、大位移的强几何非线性运动，本文使用里茨—伽辽金法求解式(3)。设覆冰导线舞动在垂直方向的位移响应为

y=ccos(ωt+φ)=acos(ωt)+bsin(ωt)

(4)

(5)

同时，对式(4)变分得：

δy=cos(ωt)δa+sin(ωt)δb

(6)

根据δa与δb的任意性，结合式(5)、(6)，在一个周期内积分，整理可得覆冰导线舞动幅值为

(7)

由于覆冰导线覆冰厚度不同，其气动系数也不同。本文使用Fluent仿真软件对覆盖不同冰厚的导线进行气动力仿真，获取气动系数三次多项式表达式，然后对该多项式的系数与冰厚rH建立函数关系式，从而得到式(7)中参数c1、c2的表达式，即

(8)

将式(8)改写为

(9)

式中k1、k2为关于式(7)的系数。

由式(9)可知，在获取导线覆冰厚度及相关线路参数后，覆冰导线舞动的幅值主要取决风速。由于气象观测点与输电线路地理位置、地形地貌以及海拔高度均不相同，故观测站风速需要经过修正，即

(10)

式中α为导线所处位置地面粗糙度因子，取值在0.1～0.5。

根据文献[22]可知，Weibull分布能够较好地描述风速的分布，假设风速序列(v1,v2,…,vn)服从Weibull分布，其概率分布函数为

(11)

式中σ为尺度参数；ξ为形状参数；v为风速。通过极大似然估计法等方法来确定式(11)中的参数σ、ξ，构造对数似然函数为

L(ξ,σ)=

(12)

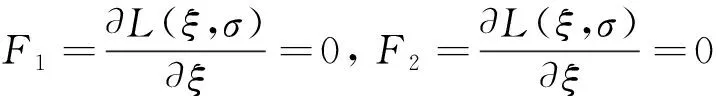
(13)

式(12)、(13)较为复杂，采用牛顿—拉夫逊迭代法求解其中参数，由式(13)可得：

(14)

其中，雅可比元素为

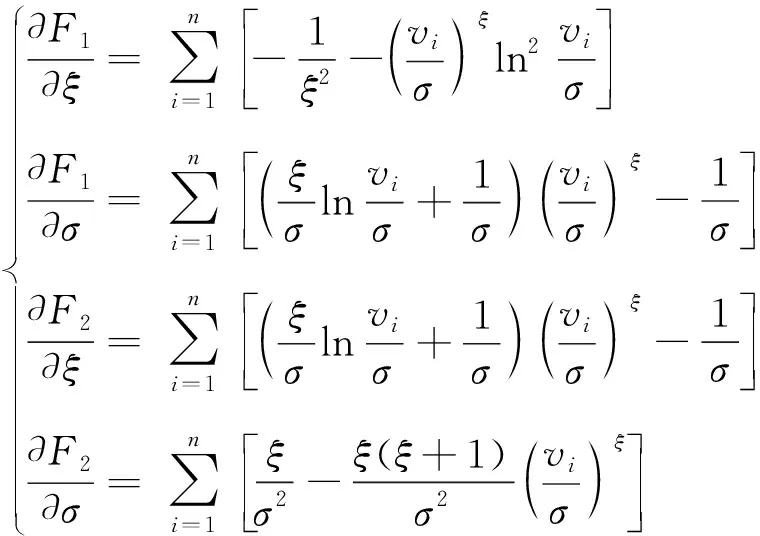
(15)

为求解式(14)，选取合适的初值，经过反复迭代直到满足max(Δσ，Δξ)<ε后，获得Weibull分布的尺度参数σ与形状参数ξ。获取两参数σ与ξ后，可以建立风速的Weibull概率分布。由式(9)可知，舞动的幅值与风速有关，经过式(9)、(11)及概率论知识可将风速的概率分布变换为舞动幅值c的概率分布，其表示为

(16)

由式(16)可知，设舞动幅值超过安全间距的概率为

Po=1-F(cse)

(17)

式中cse为覆冰导线舞动至相间最小安全间距的幅值，垂直方向上cse=Lx-Lxmin；Po为当前风速及覆冰条件下线路舞动幅值超过cse的概率。

1.2 覆冰导线非同步舞动单一幅值固有跳闸概率模型的建立

覆冰导线在某一综合条件下的舞动幅值超过相间电气安全限度时，存在发生相间闪络跳闸故障的可能。由于目前缺少导线相间非同步舞动的跳闸模型，本文以垂直布线的三相导线为例，建立导线非同步舞动的某一幅值的固有跳闸概率模型，如图2所示。

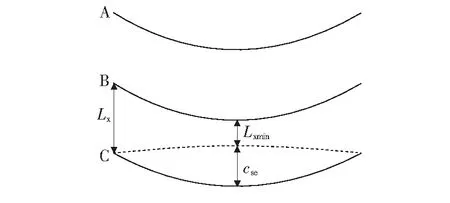
图2 导线垂直布线Figure 2 Schematic diagram of vertical arrangement of wires

假设覆冰导线的A相与C相发生舞动，将舞动时的两相导线中点位置分别为

(18)

式中ω为yA导线舞动时的角速度；φ为以C相导线为参照，A相导线舞动的相位；Lx为导线静态时的垂直相间距离。其中φ为随机值，体现了A相导线相对C相发生舞动的随机性。

当φ为0时，A相与C相导线同向舞动，由于两相导线始终保持安全间距Lx，因而不会发生跳闸事故[23]；当φ为π时，A相与C相导线反向运动，如果舞动幅值超过一定限度，两相导线将因电气间距过小或碰线而导致闪络跳闸。

基于以上分析，当导线舞动幅值越限后，A相导线在相位φ=π左右舞动时存在相间闪络跳闸区域，如图3所示。

由图3可知，如果两相导线舞动的幅值超过安全间距且其值为c，当A相导线舞动的相位φ=φx+π在区间[φ1+π,φ2+π]内时，A、C两相导线将发生相间跳闸，此时φx满足：

图3 导线跳闸Figure 3 Schematic diagram of line trip

csin(ωt+φx+π)+Lx-csin(ωt)≤Lxmin

(19)

取ωt=π/2，并将式(19)取等号可得边界跳闸相位，其表示为

(20)

由于相位为φ1+π与φ2+π的舞动波形关于ωt=π/2对称，所以在舞动幅值c超过安全间距的条件下，发生跳闸的相位区间的大小为|2φ1|。因此，舞动幅值为c时的固有跳闸概率为

(21)

2 舞动跳闸故障过程的蒙特卡洛模拟

覆冰导线舞动的闪络跳闸故障的模拟可以认为是有多个可能性的抽样[24]，其中包括确定导线舞动幅值是否越限、舞动的越限幅值及是否跳闸。以舞动的幅值是否越限为例，将舞动幅值超过安全间距的概率Po置于[0,1]区间内，并产生一个在[0,1]区间均匀分布的随机数R，R的位置表明舞动幅值是否越限，如图4所示；风速抽样与舞动是否跳闸抽样分别如图5、6所示。

图4 舞动幅值是否越限Figure 4 Galloping amplitude over limit or not

图5中，vmax为通过气象观测获取的最大风速，vo为导线刚好舞动至相间电气安全间距时的幅值co为所对应的风速，由式(9)可得：

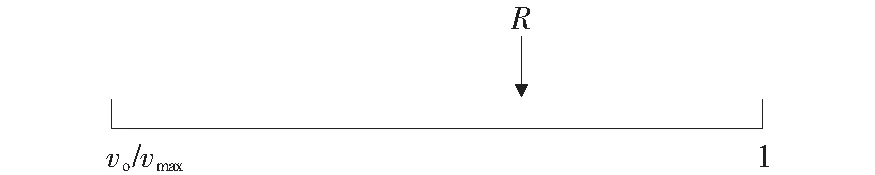
图5 风速抽样Figure 5 Sampling wind speed

(22)

使用蒙特卡洛方法可以计算一条线路第i档导线的舞动幅值越限跳闸概率Pi的统计值，根据该方法，第j次模拟过程如图7所示。

图6 舞动是否跳闸抽样Figure 6 Galloping trip or not

图7 蒙特卡洛方法计算舞动跳闸概率Figure 7 Flow chart of the calculation of the galloping tripping probability using Monte Carlo method

如果设置模拟次数为N，则每次模拟都会产生一个值为0或1的Tj。由于大数法则保证在模拟次数足够多即获得的样本足够多之后，蒙特卡洛法获取的估计值将收敛于真值，则第i档覆冰导线舞动越限跳闸概率的统计值为

(23)

对于整条输电线路，其整体舞动跳闸概率由各档导线舞动跳闸概率逻辑串联进行计算，即

(24)

式中ws为第s条线路档数。

3 求解步骤

依据线路所跨区域的大小划分气象分区，收集各分区的风速及风向、冻雨量、温度、相对湿度等信息后，基于蒙特卡洛方法的覆冰输电线路的舞动跳闸概率计算步骤如下：

1)计算各气象分区覆冰厚度，利用Fluent软件获取各冰厚条件下的气动参数；

2)利用最大似然方法估计式(16)中风速Weibull分布的参数σ与ξ；

3)依据覆冰导线舞动条件[21]，如表1所示，判断当前线路第i档导线是否发生舞动；

表1 导线起舞判断因素Table 1 Conductor galloping judgment factors

4)如果发生舞动，则转向步骤4，否则Pi=0，i=i+1，返回步骤3；

5)获取线路各档导线参数，由式(16)、(17)计算舞动幅值越限概率Po；

6)设置蒙特卡洛模拟次数为N，获取每次模拟所得的Tj并进模拟，由式(23)计算当前线路的第i档舞动跳闸概率Pi；

7)判断当前线路档数i是否小于ws，如果是，则i=i+1，返回步骤3，否则转到步骤8；

8)由式(24)计算当前整条输电线路的舞动跳闸概率PL。

本文方法计算流程如图8所示。

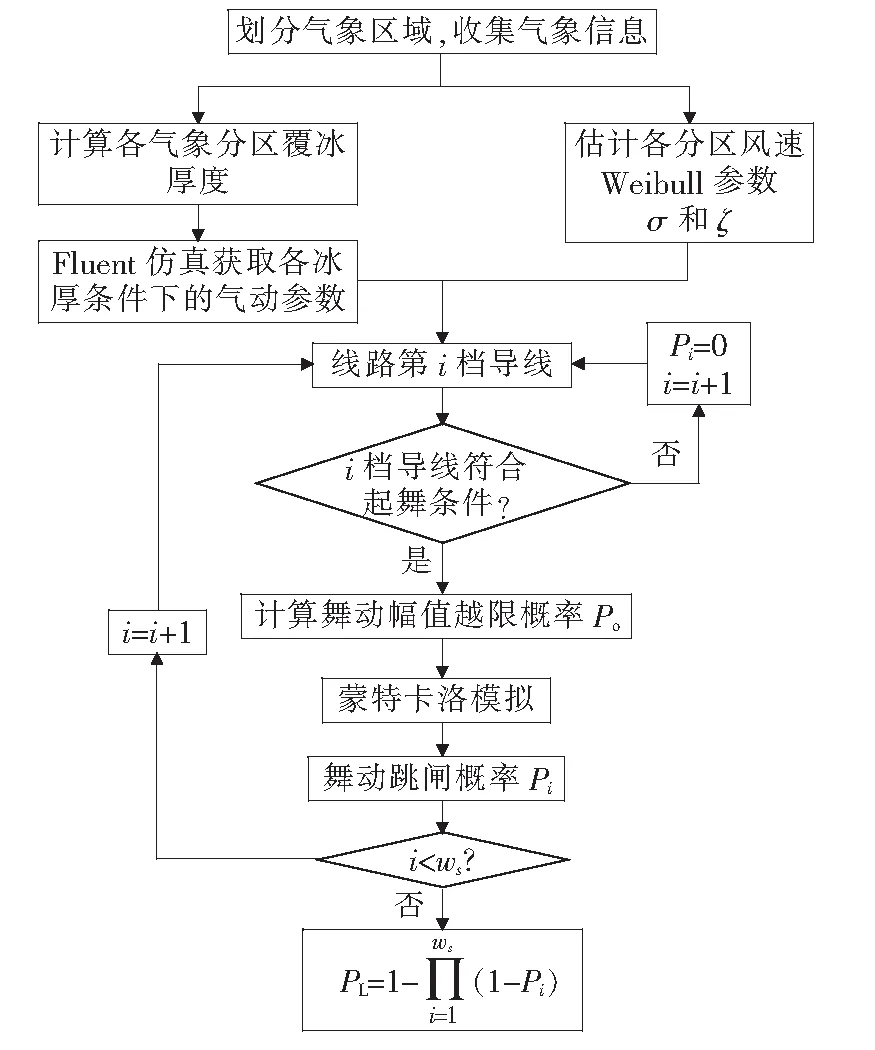
图8 计算舞动跳闸概率流程Figure 8 Flow chart of the calculation of the galloping tripping probability

4 算例分析

本文使用Fluent软件对2～25 mm冰厚的半椭圆形型覆冰导线进行气动系数模拟。Fluent软件通常用来模拟可压缩或不可压缩气体的流动，由于Fluent已经集合在ANSYS软件中，所以本文直接使用ANSYS软件中的Geometry模块建立半椭圆形覆冰导线截面模型，并使用ICEM CFD模块对覆冰导线截面进行网格划分，如图9所示。

图9 覆冰导线截面网格Figure 9 Gridding of iced wire cross section

设置图9中的右边界为气体速度入口的边界条件，左边界为气体流出的边界条件。完成导线覆冰截面的网格划分后，将网格文件导入Fluent模块中，使用适用于圆柱体绕流的K-ω湍流模型，并在导线的垂直方向上设置升力监测器以获取当前覆冰厚度与风攻角的截面升力系数。

通过旋转覆冰导线截面可改变迎面风攻角，本文对导线在不同覆冰厚度时的风攻角取值范围均设定为[-60°,+60°]，且以10°为增量。在完成全部覆冰厚度及风攻角的升力系数的测定后，先建立的各覆冰厚度时的风攻角与升力系数的函数关系式，部分覆冰厚度的气动系数曲线如图10所示。

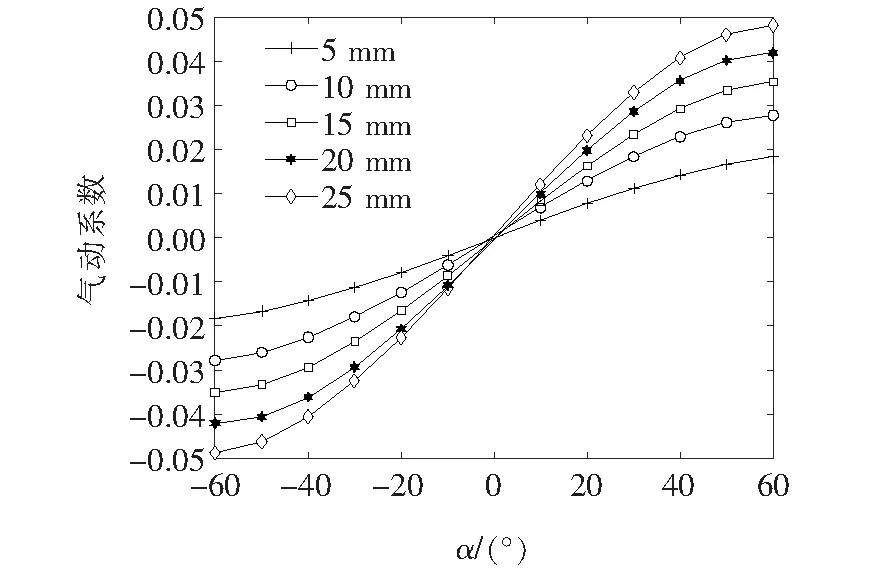
图10 不同覆冰厚度下的气动系数曲线Figure 10 Aerodynamic coefficient curves under different icing thicknesses

然后，使用三次多项式曲线拟合方法建立气动参数c1与气动参数c2关于rH的表达式，即

(25)

式(25)可代入到式(7)中以代替气动参数。

本文对2019年2月遭受冰冻天气影响的安徽宣城地区的500 kV输电线路覆冰舞动短路跳闸概率进行了计算。由于输电线路所跨区域较大，将线路所经区域划分为4个气象分区，分别获取各分区的风速、冻雨量、温度以及湿度等信息并对风速的Weibull分布进行拟合，分布函数如图11所示。

图11 风速的Weibull概率分布函数Figure 11 Weibull probability distribution function of wind speed

2月10日到12日，冻雨持续时间6 h，结合各分区气象信息判定输电线路发生舞动。根据本文方法，获取各档导线的参数及其气象分区下的Weibull分布函数，然后使用蒙卡罗方法由式(23)计算得各线路及各档舞动跳闸概率，其中山沥线单档导线舞动跳闸率如表2所示。

表2 山沥线单档导线舞动跳闸率Table 2 Single-speed wire galloping trip rate of Shanli line

对于不同线路，在各气象分区下，经式(23)计算得到各档线路Pi，由式(24)计算得到整条线路舞动越限跳闸概率PL。各条线路的舞动越限跳闸率与实际跳闸记录的对比如表3所示。

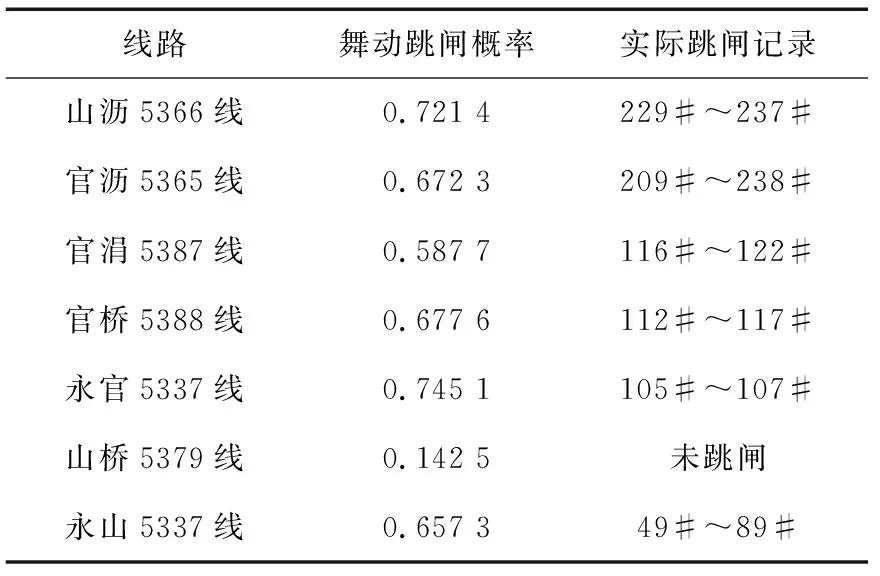
表3 线路舞动跳闸率Table 3 Line galloping trip rate

由表3可知，线路舞动跳闸率超过0.6的一些线路均发生舞动跳闸事件。计算获得的山桥线舞动跳闸概率值较小，实际中也没有发生舞动跳闸事件，分析认为山桥线处于覆冰区域边缘，且部分档导线与风向较为一致，从而破坏了起舞条件。由此可知由本文方法所获得覆冰导线舞动跳闸概率与实际故障存在关联性。从表3还可以看到舞动跳闸事件多集中发生在连续档上，考虑到连续档导线线路参数及覆冰、风速状况等较为一致，由此可知导线的舞动及其相应的跳闸事件往往集中发生在易舞动的同一气象条件下(包括风速、降雨、温度等)。