基于环境激励的连续钢箱梁桥模态测试与分析*

郭学庆，陈刚，吕松刚，王翠

(1.邵阳县公路建设养护中心，湖南 邵阳 422100；2.长沙理工大学 土木工程学院，湖南 长沙 410114)

在桥梁抗震、抗风、安全监测等领域中，结构模态参数是非常重要的参数之一，其中桥梁自振频率及主振型是进行结构动力分析和抗震设计的重要参数，也是判别桥梁在使用阶段是否存在损伤的基本依据。建筑物、汽车、机器等的实际振动模态各不相同，且每个模态都有特定的固有频率、阻尼比和模态振型，导致研究各类振动特性较复杂。通过测定结构的频率响应函数(FRF)来识别模态参数的传统频域法，由于参数难以确定，且激振信号难以实施和测定，测定桥梁结构的振动特性有一定难度。环境激励法不仅可解决传统模态参数识别方法的难题，且操作简便，基于环境激励的桥梁模态试验技术已成为工程界的研究热点。很多学者利用该技术对桥梁进行了动力特性分析，如霍立飞等在环境激励下对苏拉马都大桥主桥进行模态测试，并与理论结果对比，分析了该桥的动力特性；蒙军等基于环境激励的模态测试过程，分析了桥梁墩高变化对结构自振特性的影响；徐朔等结合有限元分析模型，对超大跨度双跨钢桁梁悬索桥的基本动力特性进行了仿真分析和结构振动试验测试。该文以某连续钢箱梁桥为例，采用基于环境激励的模态测试分析方法计算结构的模态参数，评估结构在设计荷载作用下的动力性能，并与 MIDAS/Civil有限元软件计算结果进行对比。

1 工程概况

某连续钢箱梁桥由左、右两幅组成，每幅共分为五联。左幅桥跨径布置为2×25 m(第1联)+21.5 m+21.5 m+20 m(第2联)+2×25 m(第3联)+2×25 m(第4联)+2×25 m+22 m(第5联)，桥长289.00 m；右幅桥跨径布置为3×21 m(第1联)+2×25 m(第2联)+2×25 m(第3联)+2×25 m(第4联)+3×25 m(第5联)，桥长289.65 m。左幅桥宽度17 m，横断面组成为1.5 m人行道及栏杆+4.0 m非机动车道+3×3.5 m机动车道+0.5 m安全距离+0.5 m栏杆；右幅桥宽度为15 m，横断面组成为0.5 m栏杆+0.5 m路缘带+2×3.5 m机动车道+3.75 m机非混行道+0.5 m路缘带+0.5 m安全距离+2.25 m人行道和栏杆。左、右幅桥箱梁宽度分别为17.0 m、15.0 m，钢箱梁均采用单箱四室结构形式，箱室宽度分别为3.0 m、2.5 m。

主梁截面中心处梁高1.5 m，悬臂长2.5 m，箱梁顶板、底板及腹板的钢板厚16 mm。顶板加劲肋采用8 mm厚U肋，间距60 cm；底板加劲肋采用T肋，间距40 cm。箱梁每隔2～3 m设置一道横隔板，横隔板厚20 mm。每幅桥横向设置双排墩，左、右幅桥墩中心间距分别为7.0 m、6.0 m，桥墩台基础分别采用直径为2.0 m、1.5 m的钻孔灌注桩。桥台及分联处分别设8 cm伸缩缝。荷载等级为城市-A级，人群3.5 kN/m2。结构设计安全等级为一级。

2 基于环境激励的桥梁模态测试原理

2.1 环境激励模态分析

环境激励模态分析不使用专门的激励设备，而是在自然环境荷载作用下测试桥梁结构的响应，仅利用系统的输出响应识别桥梁模态参数，特别适用于测量结构整体自振特性。结构在环境激励(如自然风、地脉动、人体行走等)作用下会产生微幅振动,而且外部的环境激励包含的频率相当丰富，可直接假设为各模态历经信号，满足模态测试试验的假设条件。

2.2 模态参数的计算原理

模态参数识别就是采用实测数据通过某种误差准则极小的优化算法确定结构系统中的模态参数，包括模态固有频率、振型、阻尼比等。

试验过程中，利用信号分析仪和振型传感器等获取桥梁结构各测量部位的环境振动响应，因为桥梁结构的跨径一般较大，加上测试仪器和加速度传感器的通道有限，试验时需假定某一点作为参考点，通常选择测试结构前二阶振型中振幅较大的点作为参考点(避免节线位置)，然后固定传感器位置。试验中通过移动各测量部位传感器位置获得全桥的振动响应，对试验所得各测点环境振动数据通过滤波除去高、低频干扰信号成分，将处理后数据进行功率谱和互功率谱分析，得到各测点信号的功率谱密度函数及各测点与基准点信号之间的相干函数和相位差函数。通过功率谱密度函数和相干函数获得各模态的自振频率，通过功率谱密度函数和相位差函数获得各模态的振型，将功率谱进行细化处理，利用半功率点带宽法获得桥梁的阻尼比。

3 试验方案

3.1 试验设计

3.1.1 测点布置

分别选取左幅桥第3联(2×25 m)和右幅桥第3联(2×25 m)进行模态参数试验，测试桥跨为二跨连续梁桥，测试目标是获得该桥前二阶模态的自振频率、振型和阻尼比。在左、右幅桥第3联每6.25 m取一个节段作为测试点，建立结构几何模型，共设置18个测点，每个横截面2个测点，其中1#～9#测点位于左、右幅桥的外侧，10#～18#测点位于左、右幅桥的内侧。

几何模型的方向设定如下：桥梁纵向为x方向，横向为y方向，垂直方向为z方向。桥梁纵向振动可忽略，垂直方向为主要测试方向。因此，每个测点测试一个方向即z方向。左、右幅桥第3联模态参数测试测点布设及测试方向见图1。

图1 结构测点布设及测试方向

3.1.2 参考点选取

测试过程需要的测点较多，而测量仪器的通道数有限。为此，选取参考点，分批次进行测试。为获得有效性较高的振型，测点数要足够多，同时控制参考点位置不动，参考点的选取避开影响模态振型的节点及桥墩等振动极其微弱的不动点。每批次测量中在参考点位置进行数据采集，并将采集的数据与参考点进行相关性计算。左、右幅桥第3联模态测试试验的参考点都位于2#测点。

3.2 试验检验

3.2.1 信号检验

信号的有效性是确保试验结果准确性的关键，通过数据有效性检验来保证信号的有效性。检验各时段每个通道信号的幅值是否相近及特性是否相似，从而判断每个采集通道是否异常，获取的信号是否有效。图2、图3分别为左幅桥6#测点和右幅桥4#测点的时间历程，曲线中包含明显的振动信号，说明干扰较小。

图2 左幅桥6#测点的时间历程

图3 右幅桥4#测点的时间历程

3.2.2 频谱分析

频谱分析是信号检验的第二步，利用频谱可准确分析信号中是否包含干扰，尤其是在系统供电不稳的情况下，50 Hz的干扰信号经常会使信号中的无效信号远远大于有效信号，导致试验失败。图4、图5分别为左幅桥6#测点和右幅桥4#测点的频谱曲线。由图4、图5可知：50 Hz干扰信号的幅值远小于有效信号，说明实测信号较好。

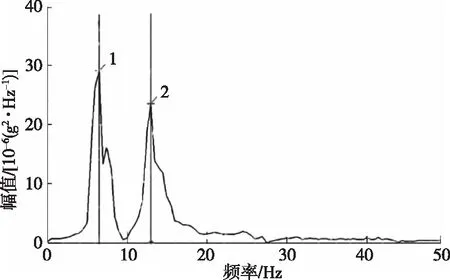
图4 左幅桥6#测点的频谱曲线

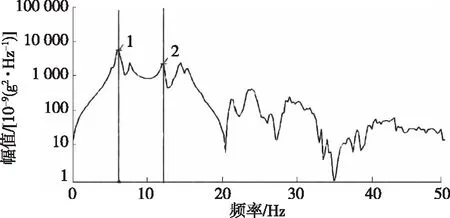
图5 右幅桥4#测点的频谱曲线

4 模态测试结果与理论计算结果比较

对测试信号进行频谱分析及模态分析，得到该桥在弯矩作用下前二阶自振频率、振型、阻尼比等模态参数。采用MIDAS/Civil有限元软件进行计算，得到该桥的理论模态参数。通过理论计算值与模态参数实测值对比，判断桥梁结构的整体刚度。

4.1 左幅桥测试结果对比分析

完成各组试验数据采集后，利用各响应测点与参考点间的互功率谱函数提取结构的模态参数，试验测试识别结果见表1。

表1 左幅桥第3联的模态参数测试识别结果

由表1可知：左幅桥第3联的1阶、2阶自振频率实测值分别为6.50 Hz、13.00 Hz。通过理论计算，得1阶、2阶自振频率理论计算值分别为5.88 Hz、8.30 Hz，均小于各阶自振频率实测值，说明该桥结构具有良好的整体刚度。1阶、2阶振型的阻尼比实测值分别为1.17%和2.52%，该桥结构具备一定的能量耗散性能。

左幅桥第3联的实测和理论1阶、2阶振型分别见图6、图7。由图6、图7可知：左幅桥第3联的理论1阶、2阶振型与实测1阶、2阶振型基本吻合。

图6 左幅桥第3联实测与理论1阶振型对比

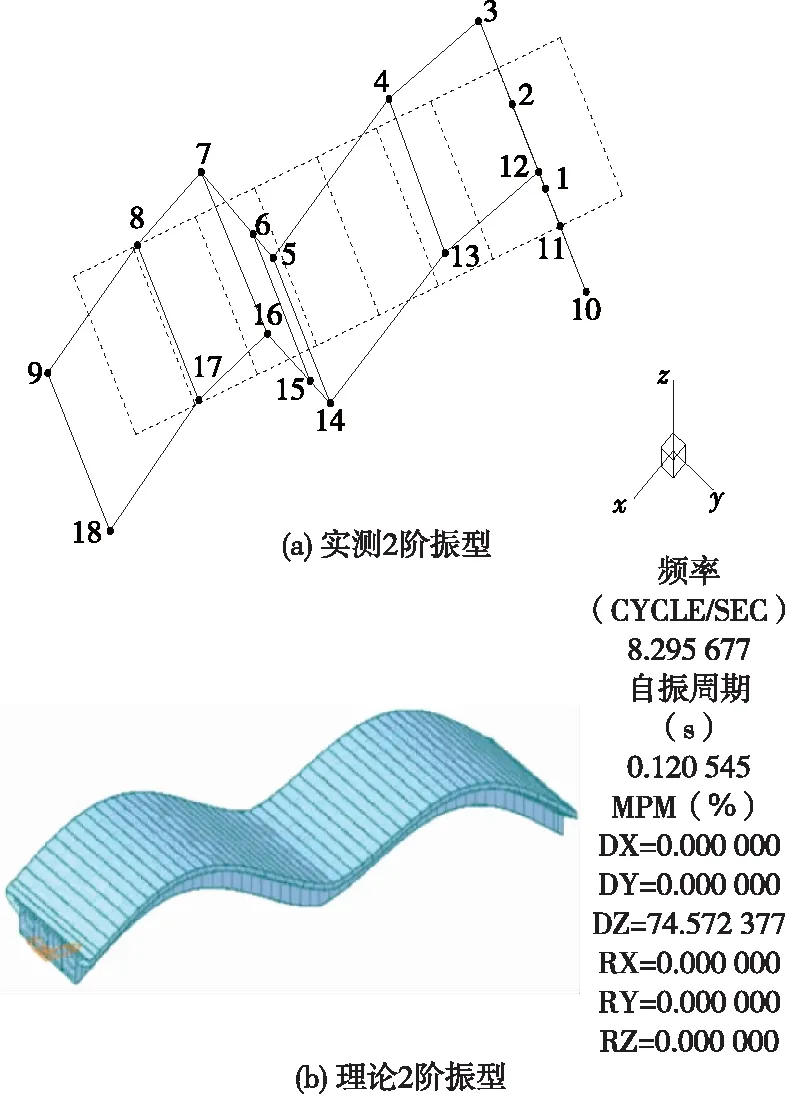
图7 左幅桥第3联实测与理论2阶振型对比

4.2 右幅桥测试结果对比分析

右幅桥试验测试识别结果见表2。

表2 右幅桥第3联模态参数测试识别结果

由表2可知：右幅桥第3联的1阶、2阶自振频率实测值分别为6.25 Hz、12.25 Hz。通过理论计算，得1阶、2阶自振频率理论计算值分别为5.84 Hz、8.25 Hz，理论计算值均小于各阶自振频率实测值，说明该桥结构具有良好的整体刚度。1阶、2阶振型的阻尼比实测值分别为2.33%、1.68%，该桥结构具备一定的能量耗散性能。

右幅桥第3联实测与理论1阶、2阶振型见图8、图9。由图8、图9可知：右幅桥第3联的理论1阶、2阶振型与实测1阶、2阶振型基本吻合。

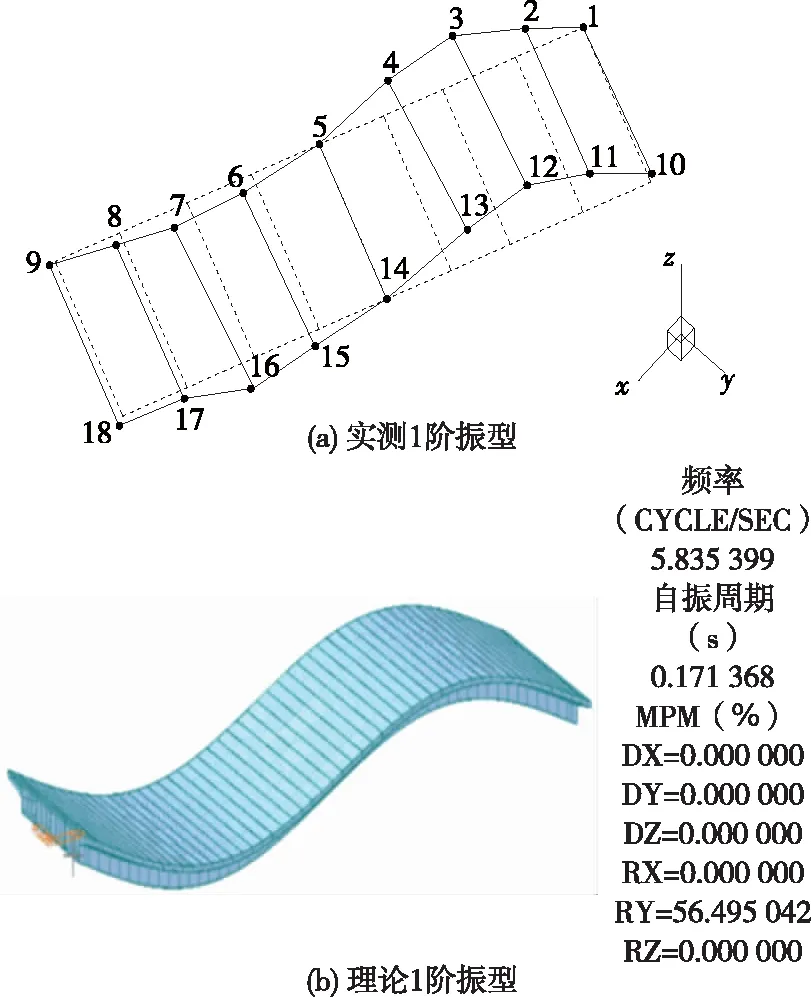
图8 右幅桥第3联实测与理论1阶振型对比

图9 右幅桥第3联实测与理论2阶振型对比

5 结论

(1) 该桥左幅桥第3联的1阶、2阶自振频率实测值分别为6.50 Hz、13.00 Hz，理论计算值分别为5.88 Hz、8.30 Hz；右幅桥第3联的1阶、2阶自振频率实测值分别为为6.25 Hz、12.25 Hz，理论计算值分别为5.84 Hz、8.25 Hz。左、右幅桥的自振频率实测值均大于理论计算值，桥梁结构的整体刚度较好。

(2) 该桥左幅桥第3联的1阶、2阶振型的阻尼比实测值分别为1.17%和2.52%，右幅桥第3联的1阶、2阶振型的阻尼比实测值分别为2.33%和1.68%，桥梁结构具备一定的能量耗散性能。

(3) 模态参数实测值与理论计算值基本吻合，采用环境激励法识别连续钢箱梁桥的固有模态参数可行。