基于监测数据的斜拉桥钢箱梁疲劳性能分析*

崔珊珊，熊文，连俊峰，赵鑫莹，宋晓东

(1.安徽省交通控股集团有限公司，安徽 合肥 230088；2.东南大学 交通学院，江苏 南京 211189)

采用结构健康监测技术可获得实时的桥梁结构响应，进而对在役桥梁结构的服役状态进行评估，对突发事件或结构异常情况发出预警。宋晓东等基于安庆长江公路大桥的拉索加速度时程，实现了拉索基准频率和索力的自动化识别，进而剔除活载效应和季节温度效应来获得恒载索力特征值。肖鑫以一座钢桁梁桥健康监测数据为基础，建立基于随机车辆荷载模型的桥梁承载力可靠性评估方法，分析了温度效应对结构承载力可靠指标的影响。夏烨等依托河北某分离式立交桥，采用小波分析从原始应变中分离出由交通荷载引起的静态响应，对比分析了不同评估周期的统计特性差异。陶兴旺等考虑桥面不平度的影响，将BP神经网络法与斜拉桥监测系统相结合对重车速度、车重进行了识别。陈一飞等基于北方冰冻海域的大跨度钢箱梁斜拉桥温度监测数据，结合国内外相关规范，提出了基于极值分析的截面内温差基准值计算方法。李嘉维等比较了环境振动测试和健康监测系统动力测试结果，通过基准有限元模型计算结果与设计计算结果的比较评估了桥梁的安全性能。

钢桥在服役过程中始终承受环境及车辆引起的变幅荷载作用，钢构件产生疲劳损伤，且随着服役期的增长损伤逐渐累积。钢桥的疲劳寿命评估一直是工程界和学术界的研究热点。黄炎等结合有限元分析和实桥疲劳试验获取扩大切口和设计切口的应力响应及面内面外应力分量，基于AASHTO LRFD规范对两类切口开展了疲劳寿命评价。韩艳等以某大跨钢桁悬索桥为背景，针对主桁梁应力关键点进行动态应变监测，基于Palmgren-Miner线性累积损伤准则及欧洲Eurocode 3规范的疲劳强度S-N曲线建立了关键构件的疲劳损伤极限状态方程。邓扬等以润扬大桥为工程背景，研究了应力循环的快速提取及应变数据中随机干扰成分的剔除方法，提出了钢箱梁焊缝的疲劳寿命预测值。陈志为基于健康监测数据提出了大跨多荷载悬索桥的疲劳可靠度分析框架。叶肖伟等提出了一种考虑钢材锈蚀的桥梁结构改进疲劳可靠度评估模型，并基于青马大桥健康监测数据对其典型焊接节点的概率疲劳寿命进行了评估。该文以某双塔双索面斜拉桥为研究背景，基于健康监测数据，通过经验模态分解(EMD)分离温度效应，采用多元线性回归验证EMD的有效性，进而得到主梁应力谱，并根据欧洲Eurocode 3规范计算疲劳寿命，对结构疲劳性能进行评估。

1 工程背景

安庆长江公路大桥为双塔双索面五跨连续钢箱梁斜拉桥，边跨设置3个桥墩，跨径布置为50 m+215 m+510 m+215 m+50 m=1 040 m(见图1)。主梁采用正交异性板结构的钢箱梁。采用电阻式应变传感器测量主梁应力，测点由北到南分别位于NO7、NA6、NO1、NJ8、跨中箱梁、SJ8、SO1、SA6、SO7的上下游顶板和U肋(N/S表示北塔/南塔，A/J表示边跨/主跨有拉索梁段，O表示无拉索梁段，离索塔越近的梁段编号越大)。梁段编号见图2，测点布置见表1。

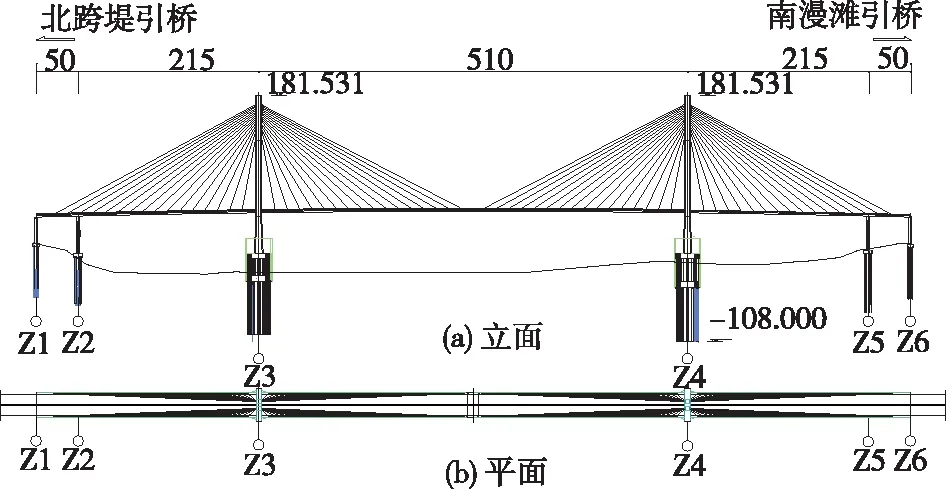
图1 安庆长江公路大桥的总体布置(单位：m)

图2 安庆长江公路大桥北塔梁段编号

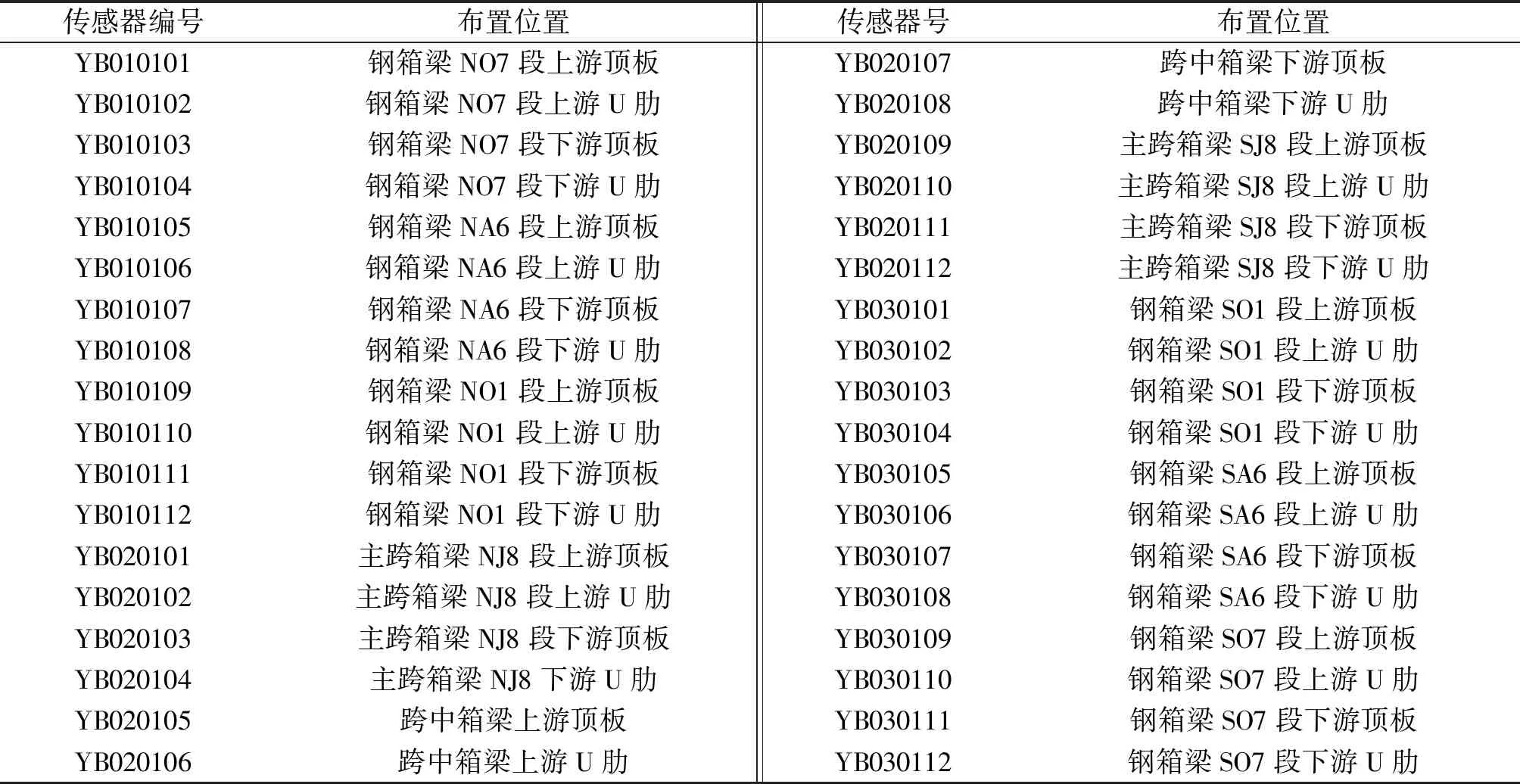
表1 应变传感器分布

2 监测数据分析

2.1 应力时程数据预处理

大跨度斜拉桥的长期监测中可能出现数据异常、缺失等情况，为得到能反映结构真实状况的有效信息，对原始数据进行异常值处理、缺失值填补等预处理。同时为方便后续应力疲劳分析，对预处理后的数据进行快慢变成分分离。图3为YB010101传感器2018年5—10月的监测数据，其中存在数据异常和缺失情况。

图3 YB010101传感器2018年5—10月监测数据

采用拉因达准则(3σ准则)检验监测数据中的异常值，对检测到的异常值通过线性插值法予以替换。对于一定长度目标数据空白的小段缺失，根据上一时间段未缺失或已填补完整的监测数据采用Hermite插值法进行填补；对于大段缺失，认为其不能有效反映结构真实信息，予以舍弃。按上述方法处理后的数据后见图4。

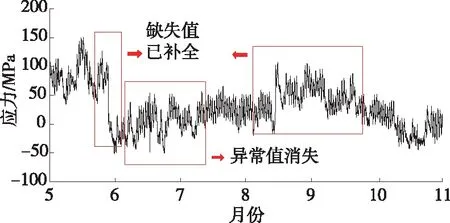
图4 处理后的数据

2.2 快慢变成分分离

桥梁结构运营过程中受到温度、风等环境荷载和车辆荷载的耦合作用，其监测数据包含快慢变成分，快变成分主要由车辆荷载和噪声引起，慢变成分主要由温度荷载引起。主梁的应力状态评估以疲劳寿命作为评估指标，而疲劳寿命的计算与应力幅密切相关，温度荷载较车辆荷载变化缓慢，应力幅大小主要受车辆荷载影响。因此，需分离出快变成分供疲劳分析。以YB010101传感器2016年6—10月预处理后的监测数据为例，对目标信号进行经验模态分解，得到10阶模态函数及残差(见图5)。

图5 EMD分解结果

为确定快慢变成分各自的本征模态函数构成，综合频幅谱的主频和本征模态函数的能量突变阶数分析阶数阈值，计算各阶模态函数的能量，结果见图6。从图6可看出：能量在第6阶附近发生突变：第1～4阶的能量持续增长，第4～6阶的能量变化平稳，第6阶又开始增长。根据能量的突变阶数，初步确定快慢变成分的阶数阈值为4～6阶。

图6 各阶本征模态函数的能量

采用快速傅里叶变换计算温度时程及各阶模态函数的频谱图，结果见图7、图8。从图7、图8可看出：温度时程的主频与第3～5阶本征模态函数的主频相同，为13.89 μHz，从第6阶开始本征模态函数的主频均小于温度时程。由于慢变成分主要由温度荷载引起，当模态函数的主频小于温度时程主频时，认为该阶模态函数属于慢变成分。

图7 温度频谱

图8 各阶本征模态函数的傅里叶频谱

综上，确定阶数阈值为5，预处理后监测数据的快变成分xq(t)和慢变成分xs(t)可按式(1)计算，计算结果见图9。

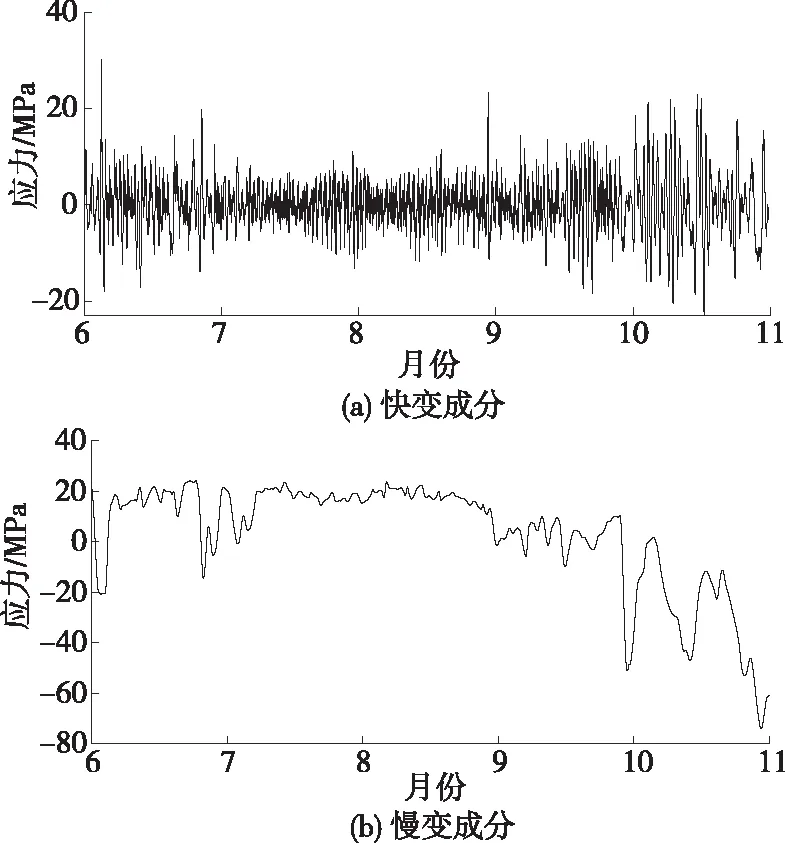
图9 YB010101传感器2016年6—10月监测数据中的快慢变成分

(1)

3 应力温度效应提取及验证

为判定分离出的快变成分的准确性，校验EMD方法的可靠性，采用多元线性回归法分离活载和温度效应，并对两种方法的分离结果进行互校。

3.1 温度效应提取

由温度变化引起的结构应力在桥梁健康监测系统采集的应力时程中占相当大比例，且这部分应力与温度具有很好的线性关系。考虑到两者的线性关系，在提取应力温度效应时将温度作为自变量，通过回归函数表达式计算温度引起的应力，同时考虑温度滞后作用的影响。函数表达式为：

Y(t)=β0+β1T1(t-nk1)+β2T2(t-

nk2)+μ(t)

(2)

式中：Y(t)为t时刻温度引起的应力；β0、β1、β2为多元线性回归参数；nk1、nk2分别为应力相对于T1、T2的滞后时长；T1为结构温度；T2为结构的日平均温度；μ(t)为随机误差。

回归参数通过最小二乘法确定，使β0、β1、β2满足下式：

(3)

当Q(βi)取最小值时，要求其对βi的偏导数为零，即：

(4)

将式(3)代入式(4)，得到如下矩阵方程：

(TTT)β=TTY

(5)

(6)

对式(5)进行求解，得到多元线性回归参数：

(7)

确定回归参数β后，对已建立的模型进行拟合度R2计算，拟合度越趋近于1，表明回归模型对目标数据的还原度越高，模型越完善。拟合度计算公式如下：

(8)

对原始数据进行预处理，处理后的应力和温度数据见图10。为确定应力相对于温度的滞后时间，将应力数据前(后)移若干长度，计算移动后的应力时程与温度的互相关系数，得到图11所示互相关系数-时间图。互相关函数图的峰值点横坐标为-3，表明由温度引起的应力相对于温度变化滞后3个数据点。由于温度的采样频率为1/300 Hz，即相邻数据点间隔5 min，应力温度效应的滞后时长为15 min。在多元线性模型的建立过程中将上述滞后时长代入式(2)，得到如下函数表达式：

图10 预处理后的应力和温度数据

图11 结构温度与应力的互相关系数-时间

Y(t)=β0+β1T1(t-3)+β2T2(t-0)+μ(t)

(9)

按式(3)～(7)计算β0、β1、β2，得到2016年6月每天的拟合参数(见表2)。

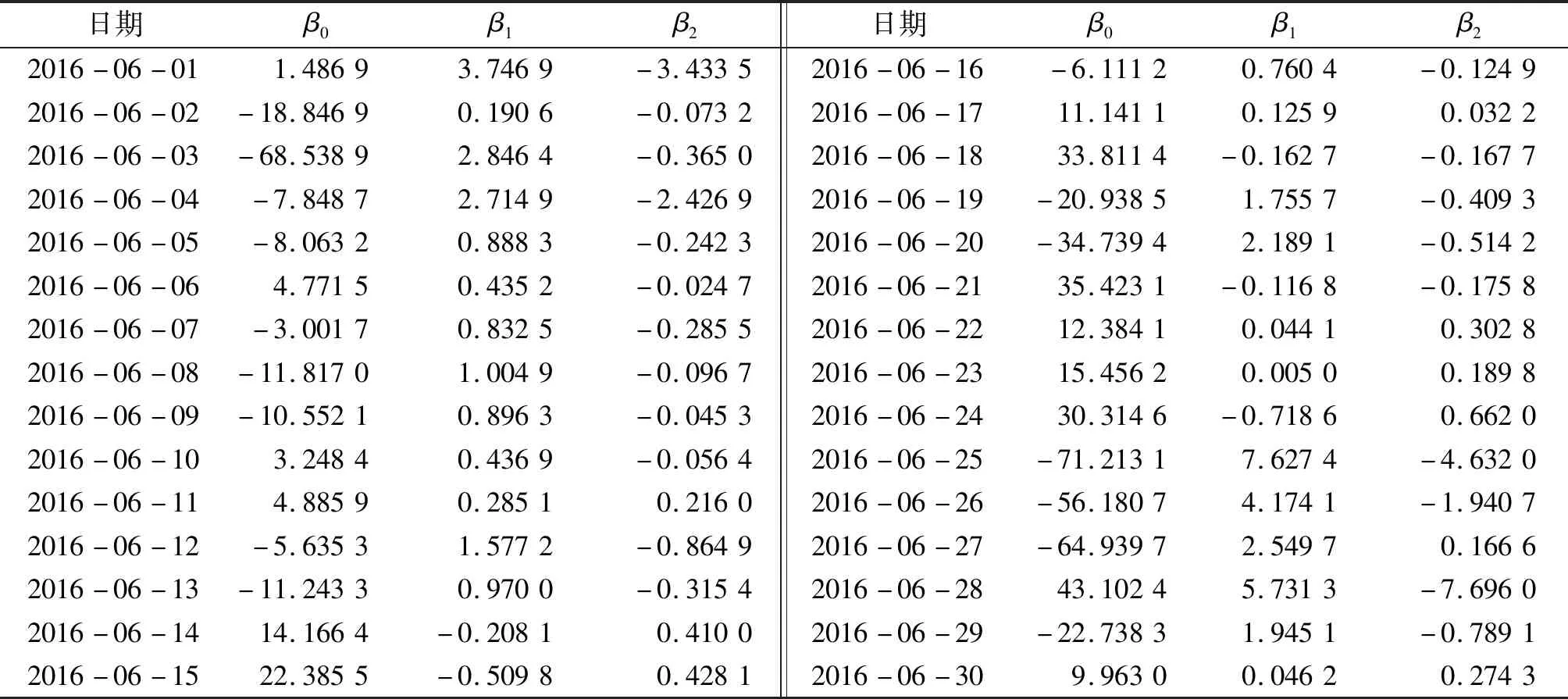
表2 多元线性回归模型参数

将表2中的β0、β1、β2代入式(9)计算每天的应力估计值，得到图12所示应力数据拟合值。按式(8)计算，得到2016年6—10月的应力拟合值与实测值的拟合度分别为0.996 1、0.908 5、0.904 8、0.914 6、0.712 2，均接近于1，拟合结果有效。

图12 实际值及拟合值对比

3.2 多元线性回归与EMD比较

考虑到活载效应的波动性较强，选择慢变成分拟合度作为互校指标进行检验。若二者拟合度大于0.8，则认为EMD分离的快慢变成分结果准确，否则重新计算阶数阈值并重构快慢变成分，直至拟合度大于0.8。通过多元线性回归法提取的应力温度效应与经验模态分解得到的慢变成分见图13，二者的变化趋势及波动范围基本一致。按式(8)计算，两种方法提取的慢变成分拟合度分别为0.871 5、0.949 3、0.800 2、0.968 8、0.803 1，均大于0.8，EMD法分离应力数据有效。

图13 线性回归法和EMD法提取的温度效应

4 应力数据疲劳分析及评估

4.1 应力疲劳分析

可根据雨流计数法求得的应力谱，按相关疲劳规范计算结构的疲劳损伤及寿命，评估大跨度桥梁结构主梁应力状态。根据欧洲Eurocode 3规范进行安庆长江公路大桥主梁应力状态评估分析。该规范定义了S-N曲线，不同疲劳细节类型ΔσC所对应的疲劳强度曲线不同。从理论上讲，小于截止极限ΔσL的应力幅不会引起细节的疲劳损伤，故截止极限被认为是疲劳作用的应力门槛。但在实际钢结构桥梁中，考虑到焊接微裂纹或钢材内部微小缺陷的存在，在高应力幅作用下“疲劳门槛”的概念不再适用。为使评估结果能更好地反映结构真实状态，将小于ΔσL的应力幅一并计入疲劳损伤计算中。

根据Palmgren-Miner线性损伤累积理论，细节承受变幅应力循环产生的总疲劳损伤为：

(10)

式中：S为细节承受的应力幅ΔσR；ni和nj分别对应ΔσR>ΔσD、ΔσR≤ΔσD时的循环次数；KC、KD为应力幅位于等幅疲劳极限。

结构的预期使用寿命为疲劳损伤的倒数，即：

(11)

4.2 应力评估

按照欧洲Eurocode 3规范的相关规定，取YB010102传感器2016年6—10月监测数据计算安庆大桥的疲劳损伤及寿命，评估其应力状态。目标数据及快变成分见图14。通过MATLAB对应力快变成分进行雨流计数，得到日应力谱。考虑到日应力谱的波动较大，为使评估结果更稳定，在计算疲劳损伤前对日应力谱进行标准化处理，得到标准日应力谱(见图15)。标准日应力谱的循环次数为当天及之前一段时间的日应力谱中对应应力幅的循环次数平均值。以每月5—18日共14 d的标准日应力谱为代表值，对各月的疲劳损伤进行计算，根据规范公式计算应力幅对应的疲劳损伤，结果见图16。按式(10)计算应力循环产生的总疲劳损伤，然后按式(11)将累计疲劳损伤转换为结构的疲劳寿命，结果见表3。

表3 桥梁结构的疲劳寿命

图14 YB010102传感器2016年6—10月监测数据

图15 2016年6—10月的标准日应力谱

图16 2016年6—10月的疲劳损伤

以计算所得疲劳寿命作为评估指标对各测点每月的应力状态进行评估，采用无量纲模型计算应力评价值。定义疲劳寿命不小于设计使用年限T0为满分状态、等于零为零分状态，两者之间按线性关系插值。单测点评价值计算公式如下：

(12)

在斜拉桥主梁应力评估中，通常认为各应力测点的初始权重相同。事实上，不同测点的应力变化对桥梁整体结构的影响程度不同。因此，在主梁应力综合评价中采用变权理论对各测点权重进行修正，计算公式如下：

(13)

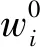
综上，主梁应力综合评价值为：

(14)

根据应力单测点或综合评价值，按表4所示评价标准判断是否需对桥梁采取相应措施。

表4 斜拉桥主梁应力评价标准

按式(14)计算各月主梁应力综合评价值，结果见表5。由表5可知：主梁应力在2016年6—10月的评分均为100，在2018年5—10月的评分均在95分以上，主梁应力状态良好。

表5 主梁应力综合评价值

5 结论

(1) 数据预处理能有效剔除监测数据中的异常值，填补缺失值，减少毛刺，提高健康监测数据用于桥梁评估的有效性。

(2) 利用经验模态分解将应力数据分解为10个本征模态函数，结合频谱的主频和本征模态函数的能量突变阶数可有效剥离数据中的温度效应。多元线性回归法与经验模态分解法互校可验证经验模态分解法处理应变数据的可靠性。

(3) 定义疲劳寿命不小于设计使用年限为满分状态、等于零为零分状态，两者之间线性插值，快速计算单测点评价值，再根据变权理论得到主梁应力的综合评价值，可实现主梁应力状态单点评估与整体评估。