灾害情况下基于改进蚁群算法的救援车辆路径优化

2022-08-09邓子杰曾传华柴李申航宇

公路与汽运 2022年4期

邓子杰，曾传华，柴李，申航宇

(西华大学汽车与交通学院，四川成都 610065)

近年来，地震、雪灾、洪灾、泥石流等自然灾害频频发生，除造成房屋倒塌、道路及设施损坏外，还引发大规模地质灾害，对社会带来不可估量的伤害。自然灾害发生后，最重要的任务是救援，然而灾后情况复杂，给救援带来很大阻挠。减少救援时间是灾后救援至关重要的一环，救援车辆路径优化又是救援时间能否加快的关键。如何利用最新的路况信息规划到达救灾目的地的最佳行驶路径，并在救援途中根据道路情况动态调整路径，提高救灾工作效率，是救援工作实施的一大核心。

蚁群算法是根据蚂蚁觅食规律提出的一种智能算法，能解决Dijkstra算法和A*算法不能解决的大规模多项式复杂程度的非确定性问题。Hsiao Y.T.等在蚁群算法的基础上提出一种全局寻优算法，在一定程度上解决了蚁群算法在多优化问题上的局部收敛问题；Kammoun H.M.等设计了一种基于蚁群算法和多智能体系结构的车辆自适应导航系统；范炯对传统蚁群算法的信息素浓度范围和更新方式进行改进，在一定程度上提高了算法的搜索性能；王晓东等基于传统蚁群算法，通过节约矩阵和信息素挥发时间曲线来引导蚂蚁搜索，一定程度上解决了传统蚁群算法存在的局部收敛问题；裴晓芳等提出一种基于模糊函数评价的蚁群算法解决路径规划问题，在一定程度上提高了迭代初期的收敛速度。以上研究主要针对常规状态下车辆路径优化，对灾害情况下车辆路径优化还需进一步研究。该文考虑灾害情况下时间紧迫性和道路动态变化等因素，建立灾后车辆路径优化模型，采用改进蚁群算法优化救援车辆路径。

1 灾后救援的车辆路径优化模型

传统蚁群算法适用于数据较小的道路地图，在道路地图过大时，道路数据的建立需要很大的内存和时间，在路径寻优时也需要更多时间达到迭代收敛，且在较宽道路上迭代出的路径呈曲折状，不符合车辆通行的实际情况。为此，在传统蚁群算法的基础上，结合运筹学中图论，使蚂蚁在进行道路寻优时从原先的路径长度、路径遗留信息素浓度转变为道路节点之间的距离长度、由路径信息素浓度演变而来的道路节点重要程度分布，以便建立灾害情况下车辆通行的相关约束条件。

灾害发生时，时间为路径选择的最优级，考虑到道路宽度对车速的影响，最优路径不一定为最短路径。因此，在传统蚁群算法模型的基础上增加图论约束，约束模型如下：

(1)

(2)

式中：MinT为目标函数，即总时间最短；Sij为节点i到节点j的路径Lij的长度；Vc(t)为t时刻车辆的行驶速度；Scmax为车辆的最大行驶里程；Vc为车辆行驶速度；Vcmax为车辆行驶最大速度；Wij为根据道路像素确定的道路宽度，取为{4,6,8,10} m；Wij(t)为t时刻车辆所在道路宽度；μ为车速控制因子。

(3)

(4)

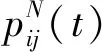
路径Lij上信息素浓度更新规则如下：

τij(t+1)=(1-ρ)·τij(t)+Δτij(t),ρ∈(0,1)

(5)

(6)

式中：ρ为信息素挥发因子，其取值范围为(0,1)；Δτij(t)为全部蚂蚁完成一次遍历后，搜索路径(i,j)上残留的信息素总和，即第N只蚂蚁在转移过程中留在路径Lij上的信息素浓度，初始时刻设置τij(0)=c，Δτij(0)=0。

改进蚁群算法将每条道路上的信息素浓度储存到蚁群算法节点中，得到Message信息素浓度矩阵Mj。Mj(t)为t时刻Message信息素矩阵中节点j的信息素浓度，反映选择道路节点的重要程度，计算公式如下：

Mj(t)=τij(t)

(7)

M1(t)=c

(8)

式中：M1(t)=c为起点的信息素浓度。

(9)

式中：Q为信息素强度，为完成一次路径搜寻后残留下的信息素总和；LN为当前仿真试验的蚂蚁完成一次搜寻后选取的所有路径长度。

2 基于图论的改进蚁群算法

算法流程如下：

(1) 截取GIS地图中部分道路作为救援车辆路径研究的道路基础模型(见图1)。设置节点时，因地图上存在一些道路缺口，补齐上方两处和下方两处位于主干道的节点，以方便后续车辆路径仿真实现。

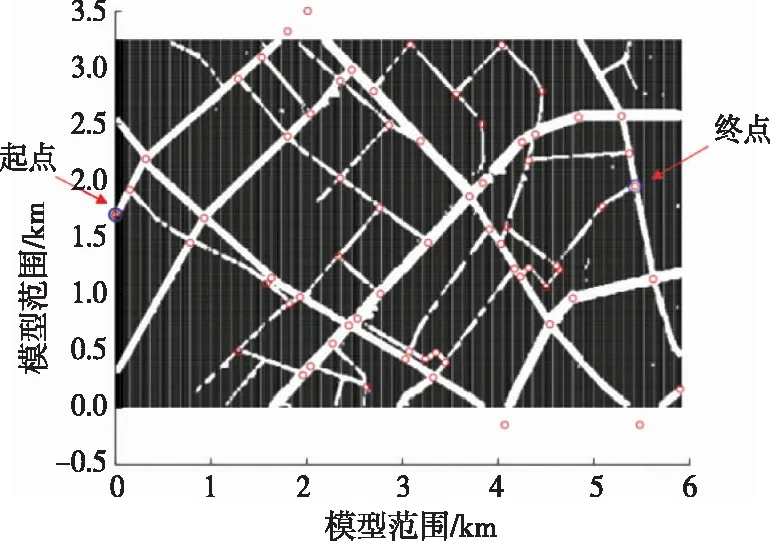
图1 道路节点示意图

(2) 在图1左侧设置起点，右侧设置终点。

(3) 设置迭代次数K、蚂蚁数量N，利用蚁群算法让蚂蚁从起点出发。

(4) 在已有节点通行数据Lij下进行迭代寻优，蚂蚁每次从节点i到节点i+1时对行进路程和时间进行记录并存储到Data文件中。

(5) 在通过节点i时在节点处将信息素浓度信息转换为节点重要程度，并储存到信息素矩阵Message中，当下一只蚂蚁位于i时，蚂蚁便可根据其可通行的所有节点的信息素浓度情况选择下一个节点。

(6) 每只蚂蚁同一次路径搜寻不得两次经过同一个节点，当无路可走或到达目标点时，寻找终止。

(7) 每次迭代选择多只蚂蚁的路径寻优结果，从中选择最优路径，同时更新信息素矩阵，当迭代趋于收敛或达到迭代次数时，结束迭代，输出最优路径(见图2)。

图2 改进蚁群算法的计算流程

3 仿真实现

对地图中道路交叉口进行节点标记，并存储到节点关系矩阵中。为便于后续仿真试验，补齐上下共4个处于主干道的节点。仿真试验中共计68个节点(见图3)，起点位于左侧，终点位于右侧。同时设置3个无人机探测障碍点。仿真区域为6 km×3.5 km。

图3 限制受灾不予通行道路后道路节点示意图

道路宽度及通行关系情况根据道路像素组成大小储存在Width矩阵中，迭代次数K=200 次，仿真试验蚂蚁个数N=500个；信息素起始浓度τij(0)=1；Mj(t)=1；信息素挥发因子ρ=0.3；信息启发和期望启发因子α、β分别取1和7；Q=1；Vcmax=120 km/h；Scmax=500 km；Wij={4,6,8,10} m；μ=15。设置4种情况进行仿真，并与传统蚁群算法进行对比，验证所建模型的有效性。

情况1：限制受灾不予通行道路、限制车辆通行最快速度和行驶里程(一般情况)。该情况下车辆路径规划见图4，迭代情况及路径长度见图5。从图4、图5可看出：车辆会较高概率选择路径相对短的小路；迭代200次后趋于收敛，最终路径长度为7.098 km。

图4 一般情况下车辆路径规划图

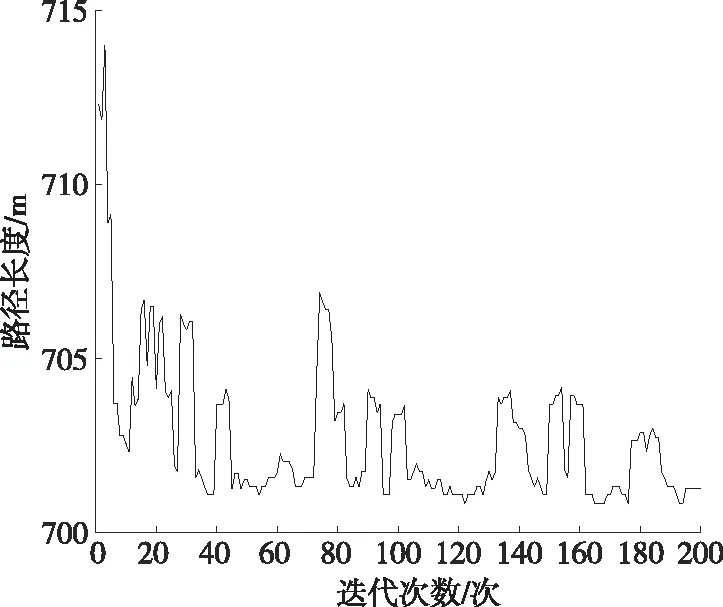
图5 一般情况下迭代情况与路径长度

道路宽度影响救援车辆的通行速度、通行安全性等，拟定路网中道路有4 m、6 m、8 m、10 m 4种宽度。情况2：设定道路宽度为4 m的路径为不安全通行道路，不予通行，通行条件为Wij≥6 m。限制道路通行情况下车辆路径规划见图6，迭代情况及路径长度见图7。从图6、图7可看出：车辆选择道路时会避开小路而优先选择副干道和主干道；200次迭代后已收敛，最终路径长度为7.204 km，车辆行驶时间为0.161 3 h。

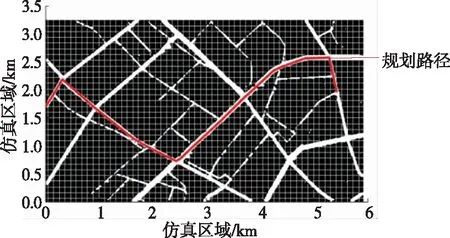
图6 限制道路通行情况下车辆路径规划图

图7 限制道路通行情况下迭代情况与路径长度

情况3：限制通行速度。前两种情况的目标函数是路程最短，而时间是灾害发生后救援救灾中的重要因素。根据道路宽度与车速的关系，道路越宽，车速越快。限制通行速度情况下车辆路径规划见图8，迭代情况及路径长度见图9。从图8、图9可看出：限制速度情况下车辆会根据车速选择耗时更短的道路；200次迭代后已经收敛，最终路径长度为7.375 km，车辆行驶时间为0.121 1 h。

图8 限制通行速度情况下车辆路径规划图

图9 限制通行速度情况下迭代情况与路径长度

情况4：限制所有约束条件(综合情况)。综合情况下车辆路径规划见图10，迭代情况及路径长度见图11。从图10、图11可看出：综合情况下车辆路径规划与限制速度时最佳优化路线相同；200次迭代后已收敛，在限制因素增加的情况下，路线的起始长度与最终路径长度相差不大，最终路径长度为7.375 km，车辆行驶时间为0.121 1 h。

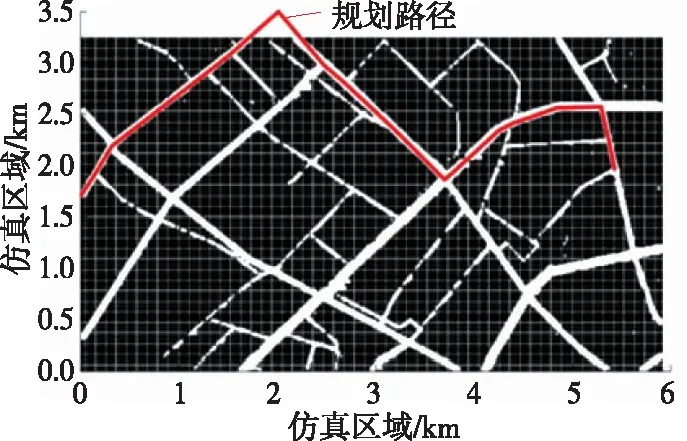
图10 综合情况下车辆路径规划图

图11 综合情况下迭代情况与路径长度

传统蚁群算法下路径规划见图12，迭代情况及路径长度见图13。从图12、图13可看出：采用传统蚁群算法进行路径规划，车辆行驶路径存在多次转折，这是因为在格栅地图中，白色道路并不一定是由单个格栅为道路宽度来组成，而可能是由2个及以上格栅为道路宽度来组成；迭代200次时趋于收敛，但并未完全收敛，由于道路中存在的折线路段较多，且路径不是最优，规划的最终路径长度为8.393 km。

图12 传统蚁群算法路径规划图

图13 传统蚁群算法迭代情况及路径长度

根据相关文献和存在障碍物的较小地图下仿真试验结果，增加迭代次数可能会在一定程度上改善转折情况，但不会完全消除。而采用基于图论的改进蚁群算法可避免这种现象的发生。由于道路提取时存在误差，在很多道路中存在断点，这种存在断点的道路在路径寻优时不满足通行条件，故采用传统算法仿真时会形成错误规划。采用改进蚁群算法可规避这种情况。2种算法的仿真结果对比见表1。

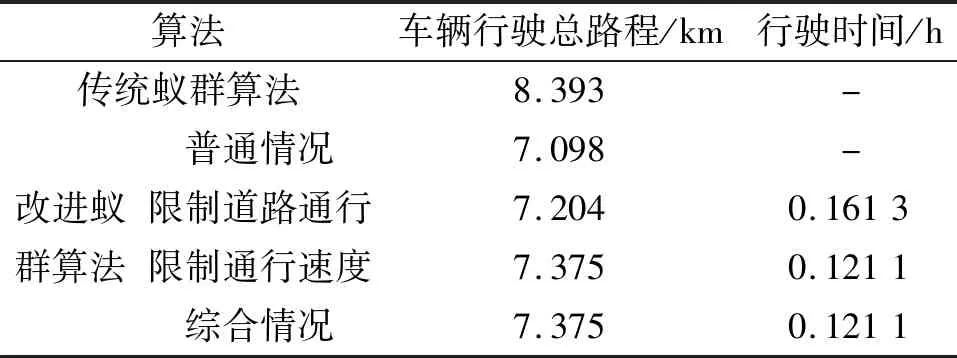
表1 不同算法仿真结果对比

从表1可看出：传统蚁群算法下车辆行驶路径最长；采用改进蚁群算法，在限制道路通行情况下，因车辆不再选择道路最窄的路段，车辆行驶总路程比普通情况有所增加；在限制道路通行速度和综合情况(限制所有约束条件)下，车辆行驶总路程相对于其他两种情况有所增加，但在目标函数时间最短的限制下，所选择道路的状况较好，在牺牲路径长度的情况下可缩短行驶时间，从而保障灾害情况下救援救灾车辆的时效性和安全性，保证救援车辆能更安全、迅速地到达救援目的地。

当车辆在救援途中识别到当前道路存在障碍点(见图14)无法满足通行条件时，通过无人机巡回飞行等方法获取备选道路信息，基于改进蚁群算法，重新规划后续车辆行驶路径。车辆根据障碍点信息重新规划的路径见图15，迭代情况及路径长度见图16。避开障碍点后规划的行驶路径长度为8.594 km，行驶时间为0.144 1 h。