基于分支有功功率的低压有源配电网拓扑辨识方法

张 巍，徐 进，刘家鹏

（上海理工大学机械工程学院,上海市 200093）

0 引言

为进一步提高智能电网服务质量,台区精益化管理成为低压配电网建设的重要任务之一［1-2］。拓扑辨识作为低压配电网智能化建设的基础与前提,其分支节点层次关系与用户区段信息的准确性将直接影响分级线损、停电管理等深化应用的实施［3］。同时,可再生能源,尤其是分布式光伏在台区的渗透率逐渐增加,也为拓扑辨识带来了新的挑战［4］。

随着配电物联网工程的推进,配电终端与分支箱监测单元的部署为提升低压配电网感知能力提供了大量的信号监测信息与量测数据［3,5-6］。学者们基于信号注入法和数据分析方法,围绕分支层次关系与用户区段信息的拓扑辨识开展了大量研究。其中,注入信号法可以通过分析设备对注入电力线的电压或电流特征信号的响应,实现连接关系的辨识。文献［5］采用工频畸变技术广播识别信号,通过脉冲电压信号轮询分析配电变压器智能终端、分支单元、用户电表的层级关系。文献［6］通过对脉冲式工频小功率信号的检测,确定网络节点自上而下的拓扑关系。该类方法的识别率虽然相对较高,但终端设备和智能电表均需要具备载波通信功能,对信号处理有较高要求,且易受强磁场等噪声源的干扰［7-8］。

数据分析方法基于数据处理技术,依据量测数据间的关联关系挖掘拓扑模型,具有灵活性高、投入小的特点［4］。传统意义上,现有研究主要依靠电压或电量的时序相关性［8-11］辨识相序或线路,同时,也有学者对分支节点与用户节点的位置逻辑进行了有益探索。文献［12］通过计算分支单元和智能电表的相关性辨识出各类设备的从属关系。文献［13］首先利用电压幅值对低压拓扑分层,然后分析了邻层节点间电量矩阵的主成分识别相序关系。当相邻层之间的线路区段有用户接入时,限制了节点电量的有效匹配,不利于重构多层次拓扑。此外,低压有源配电网潮流双向多变,当高比例分布式能源接入系统后,会抬升节点电压［14］,无法保证电压幅值按梯度依次降低的假设成立。可见,上述数据分析方法大多利用多类型数据实现拓扑还原,但针对树形拓扑网络,仅利用有功功率辨识分支层次关系和用户区段信息在国内外文献中还鲜有涉及。

因此,本文提出一种基于分支有功功率的低压有源配电网拓扑辨识方法。首先,基于时频变换与特征提取分析分支节点功率序列的耦合相关性,辨识分支节点的层次结构。在此基础上,以线路区段的形式划分低压配电网,基于线性变换与回归分析方法,分析区段与用户节点功率的逻辑加和关系,实现用户所属区段的定位。然后,通过邻接矩阵表征分支节点与用户节点的连接关系。最后,通过算例验证所提方法的有效性。

1 低压有源配电网的拓扑辨识

1.1 低压有源配电网结构

典型的低压有源配电网拓扑如图1 所示,可以抽象为一个以台区配电变压器（简称配变）终端为根节点的辐射状树形网络。除低压母线之外的线路可以划分为主干线和接户线。主干线以三相四线铺设,通过设置分线箱引出三相四线分支［15］,分支监测单元（简称分支单元）用于采集分支线路处的有功功率。以分支单元的拓扑关系为基础,将相邻上下分支单元之间的各相线路、末端分支的各相线路定义为线路区段。接户线则通过三相四线制或单相双线制从线路区段中引出,并为三相用户或单相用户提供电能。其中,多数用户连接在末端分支的各相线路上,部分用户连接于相邻分支单元间的主干线路［11］。随着小容量光伏电源不断接入用户侧,可再生能源的渗透率不断提高,根据用户是否安装光伏发电系统将低压配电网中的用户划分为光伏用户和非光伏用户。在对低压网络节点建模分析时,将台区配变终端与分支单元建模为树形拓扑的分支节点,用户处智能电表为用户节点。

图1 低压有源配电网的拓扑Fig.1 Topology of low-voltage active distribution network

1.2 拓扑辨识问题描述

低压配电网拓扑复杂,主干线上存在大量分支,底层智能电表部署位置繁多,分支节点间的层次逻辑关系、准确的用户拓扑档案等重要信息难以获取［6］,导致拓扑辨识过程中存在诸多难题。

1）辨识分支节点的层次关系。因线路分布错综复杂,分支节点上下与并行信息不明确,基于分支单元的特征信号进行辨识［5-6］,信号处理要求较高。当光伏接入比例较高时,反向潮流显著,节点电压可能会越限,在同一电压等级下,依靠电压幅值划分层次关系［13］,可能会导致层次关系的误判。

2）实现用户的区段定位。区段定位多出现在配电网的馈线自动化中,以作为配电网故障隔离与恢复的前提。类似地,本文将上下游分支节点之间、末端分支的各相线路描述为线路区段,辨识用户连接区段的过程表述为用户的区段定位。与放射式结构相比,树干式低压配电网多是由分支节点按层堆叠而成的辐射式网络结构。此外,用户接入的层次位置没有规律,仅通过“低压线路-相序-户表”关系,难以获取用户的区段信息。

1.3 总体思路分析

针对上述问题,所提低压有源配电网拓扑辨识方法的核心思想为:基于分支节点的有功功率,通过分析功率序列的耦合相关性,获取分支节点的层次关系；参照层次关系得到区段功率,基于区段与用户节点功率之间的逻辑加和关系,识别用户所属的区段,进而实现拓扑结构的辨识。

为了提取关键的节点连接信息,依据图论知识描述低压有源配电网拓扑结构,其拓扑图可以表示为一个无权无向图G=(V,E)。 其中,V={1,2,…,nall}为网络的节点集,nall为节点个数；E={exy}为网络的边集合,exy为节点x和y之间的连线。将图G的邻接矩阵表示为A,若节点x和y不存在连接关系,则元素Axy=0；若节点x和y存在连接关系,则元素Axy=1。当节点x更接近根节点时,节点x和y分别为父节点和子节点。 设D={1,2,…,N}为分析时段的时间断面集合,N为量测数据的采样点数。因此,算法旨在基于V的有功功率数据,通过求解邻接矩阵A进行网络拓扑结构的辨识。为直观地表示网络节点在不同时刻的量测值,对功率数据集进行矩阵化,即

式中:PC为用户节点的功率矩阵；nc为用户节点个数；PC,cj为j时刻用户节点c的功率测量值。

需要说明的是,由于三相用户可视为3 个单相用户,以光伏用户的净功率、非光伏用户的负荷功率作为用户节点功率。当光伏电量无法就地消纳而上网时,光伏用户的净功率为负。

利用节点有功功率数据辨识拓扑的具体步骤如下:首先,通过分支节点有功功率矩阵PB的时频变换进行特征提取,基于突显的特征采用相关性分析辨识分支节点的父节点,逐步更新分支节点邻接矩阵AB,得到分支节点层次关系结果,以表征分支节点的上下关系、并行关系、相序关系。进一步,利用邻层上下游分支单元各相节点的有功功率差值、末端分支各相节点的有功功率,生成线路区段的有功功率矩阵PL。然后,在考虑数据误差的同时,对用户节点的有功功率矩阵PC与PL进行线性变换,利用回归分析实现用户区段的定位,并构建用户节点关联矩阵AC,以体现用户的区段信息。最后,对AB与AC进行映射,建立拓扑邻接矩阵A,上述辨识原理如图2 所示。

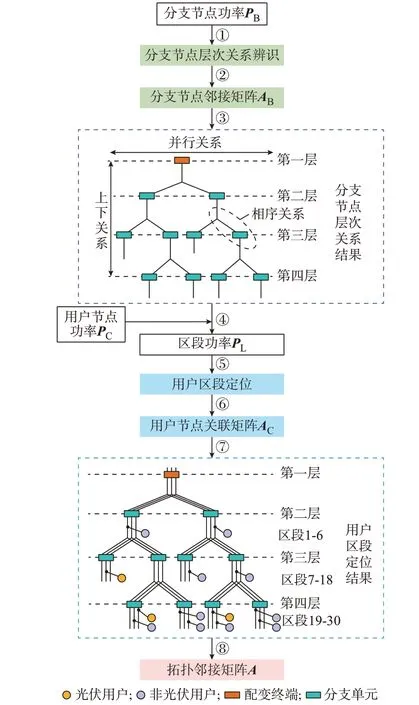
图2 利用功率数据辨识拓扑的原理Fig.2 Principles of topology identification using power data

2 基于时频变换的分支节点层次关系辨识

上下分支节点通过台区主干线相连,功率序列间存在一定的耦合相关性。由于部分用户连接于相邻分支节点间的线路,以上、下分支节点分别为父、子节点进行相关性分析时,需要保留真正父子节点的序列特征并放大非父子节点的相对差异。因此,本章首先对功率序列进行频域滤波,获取蕴含细节波动特征的高频分量,然后提取分量中的时序变化特征并构成特征矢量［16-17］。通过相关系数衡量特征矢量的相关性,判断所分析分支节点的父节点,逐步构建分支节点层次关系。

2.1 分支节点邻接矩阵的初始化

考虑到分布式能源出力的间歇性,在不存在反向潮流的时间断面集合Y⊂D内,沿线流经的有功功率逐渐递减,即流经上游分支节点的功率大于下游分支节点的功率。据此特性初步筛选出各分支节点可能的父节点,通过初始化分支节点邻接矩阵AB的元素,缩减后续节点相关性分析的范围。值得注意的是,Y仅用于判断潮流方向,后续分析仍利用采样时段D内的N列数据。对于含分布式光伏电源的台区,可将Y设定为夜晚时段。根据功率矩阵PB,对各个分支节点在Y时段的三相有功功率累加,并按照累加数值从大到小的次序对其排序得到数组{Sb}(b=1,2,…,nb),即S1≥S2≥…≥Snb,其中,Sb为分支节点b的功率累加值。由此可见,分支节点1 即为根节点。基于{Sb}对所有分支节点遍历并进行数值比较后,可以形成初始的AB,即

式中:Sx和Sy分别为分支节点x和分支节点y的功率 累 加 值；AB,xy为 矩 阵AB第x行 第y列 的 元 素,若AB,xy=1,则节点y可能是节点x的父节点。

2.2 功率序列的频域滤波

此时,由于分支节点之间的相序关系未知,通过读取分支节点在时刻j(j=1,2,…,N)的三相功率并将其求和,将任意分支节点的功率量测值合并为单行序列,即PB⇒PBS,其中,PBS为合并后的分支节点功率矩阵。从频域审视上述矩阵的行向量并进行频谱分析,将节点的能耗行为解析为低频稳定分量和高频随机分量。其中,低频稳定分量为分支节点的共有特性；高频随机分量因能耗特性而异,其蕴含了分支节点独特的能量特征［16-17］。为突出不同分支节点功率序列之间的差异性,使用基于频域分析法获取高频随机分量［18］。首先,利用快速傅里叶变换（fast Fourier transform,FFT）将功率序列由时域变换至频域；其次,参照文献［16］处理离散负荷序列的方法,依次设置采样频率fs与截止频率fcut,通过将频率低于fcut的幅度设置为零的方式实现低频分量与高频分量的分离；然后,提取频率响应中的高频随机分量；最后,经频域滤波后,再利用逆快速傅里叶变换（inverse fast Fourier transform,IFFT）将高频随机分量由频域转换至时域,表达式为:

式中:PH,bj为分支节点b在j时刻的高频功率值。

2.3 时序数据的特征提取

对于台区拓扑相连的两个上下节点而言,当下级节点的功率值增加或减少的程度较大时,上级节点的功率值也可能增加或减少。特征提取就是提取下级节点较其他节点功率变化更明显的特征点。

通过计算任意两个时刻之间节点的功率变化,使适合提取的特征突显出来。利用基本统计方法,提取高频功率序列蕴含的显著性变化特征与极值点特征。对公式（7）中PH的任意两列作差,构造列数为Ncha=N(N-1)/2 的功率变化矩阵P͂H。从所用数据的角度来看,关注的是功率值的变化,并非功率值本身。此时,矩阵的列数有所增加,即

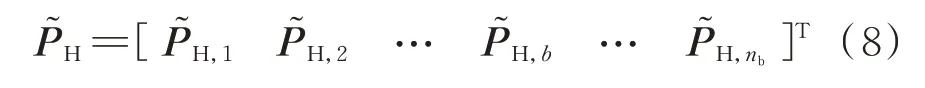
式中:P͂H,b为节点b功率变化的向量。

显著性变化是指在相同的时间间隔,所分析节点的功率变化明显高于其余待识别分支节点的变化总和［16］。为说明流程,以节点p(p=2,3,…,nb-1)作为子节点为例进行分析,将公式（9）作为提取准则获得节点p的特征矢量,矢量元素的计算式为:

式中:Mext{∙}为求极大值或极小值的运算；P͂H,pr为节点p在第r(r=2,3,…,Ncha-1)次功率变化的数值。

2.4 特征矢量的相关性分析

对于分支节点p而言,与其直接相连的上游分支节点的特征矢量相关性大于不直接相连的分支节点的特征矢量相关性。采用皮尔逊相关系数ρ作为特征矢量P̂H,p与P̂H,q的相似性评估量［2］,如下所示:

此外,为了能够通过辨识分支节点p的兄弟节点的方式,获取节点的并行关系,将式（8）中子节点p的 行 向 量P͂H,p从P͂H,qpar中 剔 除,以 提 高 后 续 过 程 中其兄弟节点与父节点qpar的相关性,即

重复式（8）—式（15）,依据初始的AB,按照遍历的方向逐行辨识,直至识别出所有分支节点的父节点,并由最终的AB获得分支节点的上下与并行关系。

2.5 分支节点相序关系的辨识

需要指出的是,在第2.2 节中,对任意时刻分支节点的三相功率进行累加,辨识了分支节点的上下与并行关系,但此时没有任何的相序关系。对于相邻的上下分支节点而言,同相节点之间的功率相关性远大于异相节点之间的功率相关性。因此,根据已建立的层次关系,以分支节点及其兄弟节点的各相节点作为子节点,其邻层上游分支节点的各相节点作为父节点集合。借助上述父子节点辨识方法分析子节点与各个父节点的相关性,确定节点间的相序关系。将识别的相序信息融合在邻接矩阵中,得到最终的分支节点邻接矩阵AB。为说明分支节点上下与并行、相序关系的辨识流程,以5 分支节点网络为例进行可视化展示,具体如附录A 图A1（a）所示。

3 基于回归分析的用户区段定位

依据融合相序信息的分支节点层次关系,可以直接得知低压网络中的ntb条线路区段。另外,对于辐射状的低压有源配电网而言,供电线路路径唯一,且每个用户仅属于一条线路区段。因此,基于能量守恒定律,在任意量测时段,任意一条线路区段的功率均等于该区段下所有用户节点的功率总和加上该时段的有功损耗与误差,即在逻辑上,线路区段与用户存在功率加和的关系,这种约束特性能够准确地反映两者的归属联系。针对此约束特性,结合回归分析理论,通过求解区段与用户节点间的回归矩阵,可以实现用户的区段定位。

3.1 线路区段功率的计算

根据分支相节点的功率矩阵PB,相邻层次间的线路区段功率可由上下游分支节点各相节点功率逐次相减得到；末端分支区段的功率可由PB直接获取。因部分区段未接入用户,为滤除线损的干扰并高效地发现区段是否存在用户,通过设定阈值对线路区段进行筛选,确定被用户所连接的nl线路区段,并以此生成区段功率矩阵PL,即

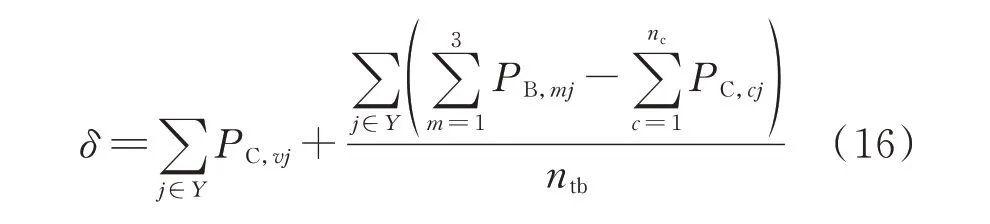
式中:δ为功率阈值,若某一线路区段在Y时段内的功率累加值不小于该阈值,则说明该线路区段有用户接入；v为在Y时段内消耗总功率最小的用户编号；PC,vj为j时刻用户v的功率测量值。

3.2 用户区段定位模型的建立

为简化分析,将线路区段等效为父节点,其节点数量为nl,功率矩阵为PL；将用户节点等效为子节点,其节点数量为nc,功率矩阵为PC；父子节点总数记为nlc=nl+nc。随后,本文借鉴文献［13］的研究思路,将用户的区段定位描述为深度为2 的父子节点层次模型辨识。其基本思想是基于约束特性,在考虑数据误差的同时,对父子节点的功率矩阵进行线性变换得到约束矩阵；在此基础上,通过求解的回归矩阵,直观地展现父子节点的连接关系。

3.3 数据误差的处理

由于有功损耗、计量设备不可避免地存在误差,直接依靠约束关系辨识难以进行。一般而言,父子节点的功率差值取决于导线损耗、测量误差。

导线损耗通常由节点的负荷特性及线路参数决定,由于缺乏较为完整的线路参数信息,无法直接通过潮流计算得到。因此,本文采用父子节点的功率值对导线损耗进行分摊与估算。令PLF为父节点功率矩阵PL减去导线损耗后的功率矩阵,其中,父节点l(l=1,2,…,nl)在j时刻的功率修正值PLF,lj为:

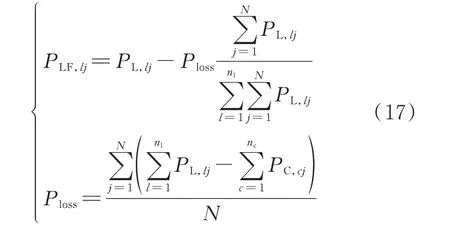
式中:PL,lj为j时刻父节点l的功率测量值；Ploss为采样时段D内导线损耗的平均值。

修正线路区段的功率值后,将父子节点的量测功率矩阵表示为PM=[PLF,PC]T。

测量误差主要由仪表更新率、计量误差、延时偏差这3 个部分组成［20］。仪表更新率是指电压或电流互感器的采样周期,一般设置为0.2 s［21］；计量误差取决于电能表的精度,可以利用节点量测的均值建模［22］；延时偏差是指计量设备仪表不同步引起的误差,参照文献［13］的研究实现误差建模。在计及仪表更新率的同时,采用ξ近似代替父子节点的测量误差矩阵。因各个电能表的测量误差相互独立,节点i(i=1,2,…,nlc)的行向量ξi近似服从均值为0、方差为σ2i的正态分布。σ2i的表达式为:

式中:Σ为nlc行nlc列的对角阵,对角元素Σii=σ2i；L为nlc行nlc列的下三角矩阵；PLE和PCE分别为嵌入误差的父节点功率矩阵和子节点功率矩阵。

3.4 用户区段定位模型的求解

3.2 节中区段定位模型的求解建立在数据内在约束的基础上,其数学本质是数据匹配。据此,首先对功率矩阵进行维度归约,即引入线性变换中的奇异值分解（singular value decomposition,SVD）对矩阵PME进行降维。然后,对相关的特征向量进行反变换,求解蕴含匹配信息的约束矩阵J,具体为:

式中:JL和JC分别为矩阵PLE和PCE的约束矩阵；Z͂为回归矩阵。

由于对导线损耗、测量误差进行了近似求解,对Z͂的元素进行四舍五入计算,可以求得最终的回归矩阵Z。具体来说,若元素Zlc=0,表明子节点c不属于父节点l；若Zlc=1,表明子节点c属于父节点l,即用户节点c在线路区段l上获取电能。可见,矩阵Z确定了用户与线路区段的归属关系,等效为点与边的联系。下一步,纳入在3.1 节中被筛除的线路区段,并根据用户与区段的归属关系,形成用户节点关联矩阵AC,表达式为:

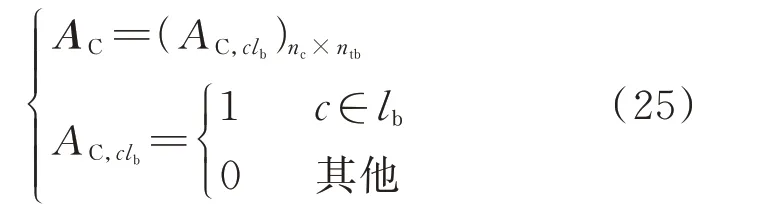
式中:lb(lb=1,2,…,ntb)为全部区段的编号；当用户节点c接入线路区段lb时,AC,clb=1,否则为0。

为直观地说明用户区段定位流程,继续以5 分支节点网络为例进行可视化展示。由分支节点的层次关系判定该网络的线路区段数量为15,通过上述方法获取用户节点关联矩阵,有效地实现了20 个用户的区段定位,如附录A 图A1（b）所示。

在用户节点关联矩阵AC基础上,以区段的上游节点作为用户节点的邻接节点,结合最终的分支节点邻接矩阵AB,并通过矩阵映射的方式,建立图G的拓扑邻接矩阵A。需要说明的是,映射是指基于固定且唯一的边关系,对邻接或关联矩阵的表达形式进行变换,从而实现矩阵的融合。综上,获取邻接矩阵A的整体流程如附录A 图A2 所示。此外,在放射式结构中,多条分支馈线以三相四线制的形式引出。根据配变终端与分支馈线各相、分支馈线各相与用户电表的功率逻辑加和关系,分别计算它们的回归矩阵,从而实现配变终端-线路-户表关系的辨识。

4 算例分析

4.1 算例数据描述

为验证所提方法的有效性,本文以附录A 图A3所示的台区拓扑作为研究对象。借鉴文献［20,23］所用方法,利用配电网仿真平台OpenDSS 搭建低压有源配电网时序稳态仿真模型。在三相四线制潮流计算中,采用中国某市某低压配电网的用户负荷数据,将变压器低压侧设置为平衡节点,在考虑光伏出力的同时计算分支节点的有功功率,并与用户功率共同构成测试数据集。其中,用户负荷为60 min 采样间隔的有功功率,功率因数在0.92～0.98 之间随机分布。预设U10、U27、U30、U33、U48、U80 为配置双向智能电能表的光伏用户,其发电系统采用恒功率控制方式［24］,装机容量在5～15 kW,结合典型气象年的气象数据输出上述6 个光伏发电系统的出力序列。为评估方法的性能,考虑多重因素实现样本数据集的创建。

1）能量渗透率。根据可再生能源渗透比例［25］,将低、中、高比例下的光伏渗透率分别设置为8%、15%、35%。通过控制光伏发电系统的投切模拟不同的能量渗透率,具体如附录A 表A1 所示。不同渗透率下的配变净负荷曲线如附录A 图A4 所示。

2）数据样本。在工程应用中,一般数据量越大,对分布式系统存储与通信传输的要求就越高［20］。因此,本文以7、15 d 的样本数据为例进行测试。

3）测量误差。常用有功电能表的精度α可分为0.2、0.5、1.0、2.0 这4 个 等 级［26］,即 计 量 误 差 分 别在±0.2%、±0.5%、±1.0%、±2.0%以内。为考虑计量同步性误差,通过功率值的偏移模拟0～10 s 的延时偏差［20］。考虑延时偏差的同时,添加相应的高斯噪声代替潮流的实测数据。针对每种均值为零、方差固定的噪声,利用蒙特卡洛方法生成误差分布场景,通过求解所有场景相关系数或准确率的平均值,评估该误差下方法的性能。

4.2 拓扑辨识结果

为进一步测试本文所提方法,本节将测量误差设置为0.5%,分别展示3 种能量渗透率下,7、15 d（即采样点数N分别为168、360）数据样本的分支节点层次关系和用户区段定位的辨识结果。

1）分支节点层次关系辨识结果

拓扑辨识过程中,首要的目标是基于45 个分支相节点的功率矩阵PB得到分支节点的上下、并行、相序关系,具体流程如下。首先,将18:00 至凌晨05:00 的采样时段中对应的时间断面集合设置为Y,根据PB计算时段Y内各个分支节点的三相总功率；通过得到附录B 图B1（a）所示的初始化的分支节点邻接矩阵AB1,初步判断节点可能的上下关系。然后,对分支节点在采样时段D内的功率序列进行时频变换与特征提取,基于提取的显著性变化及极值点特征形成特征矢量并进行相关性分析,依次辨识分支节点的父节点；通过得到附录B 图B1（b）所示的分支节点邻接矩阵AB2,表示分支节点的上下与并行关系。最后,结合上下与并行关系,以配变智能终端的相序为参考,将上述辨识算法再次用于邻层分支节点的相序辨识；通过融合相邻节点间的相序信息得到附录B 图B1（c）所示的邻接矩阵AB,从而反映分支节点具体的层次关系。

为展现辨识过程中分支节点特征矢量间的相关性,图3 给出了测量误差为0.5%、500 种误差分布场景、能源渗透率为8%时,两类数据样本下各个分支节点与其真正父节点的相关系数、真正父节点与其次可能父节点的相关系数差值。

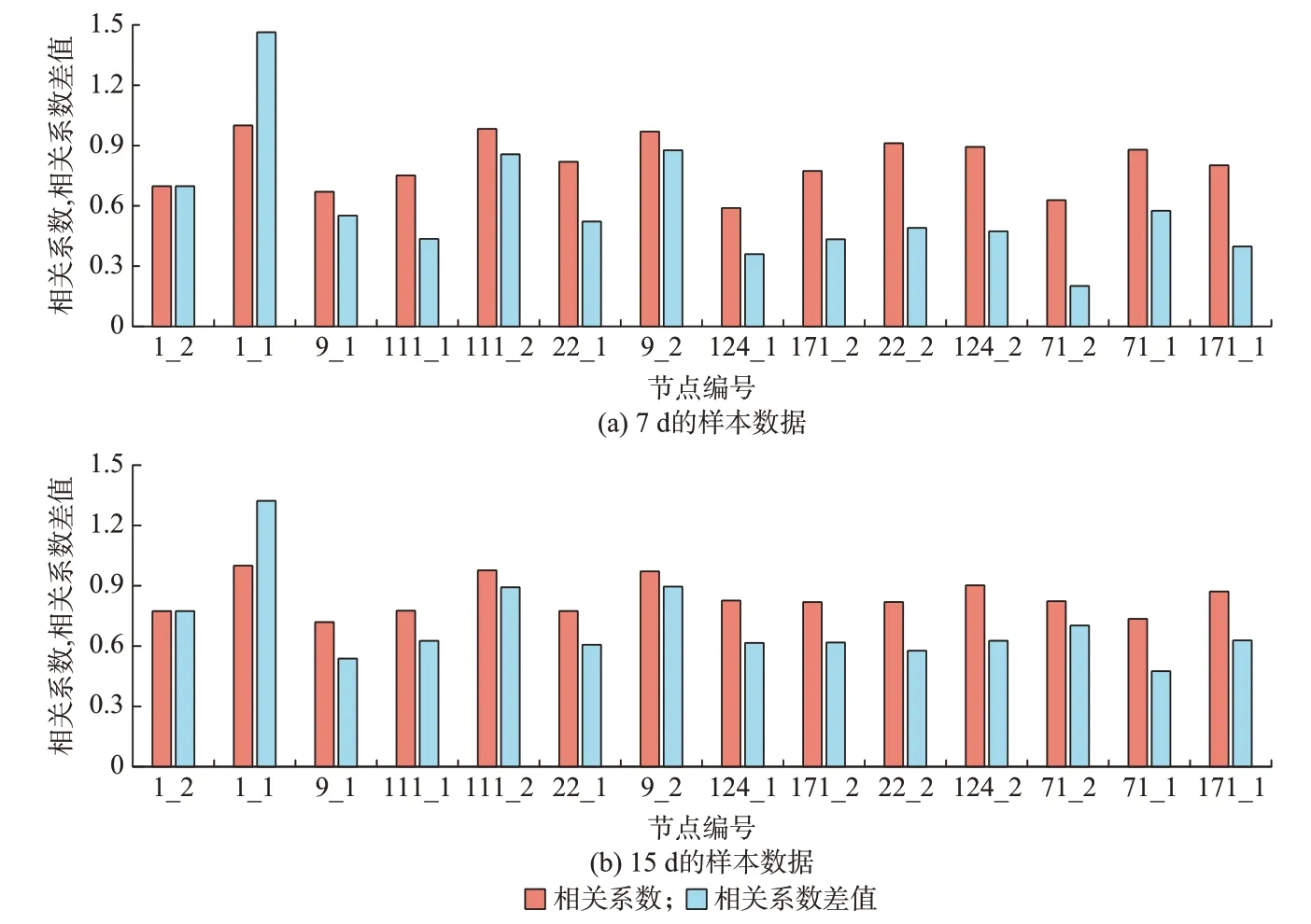
图3 两类样本相关性分析的结果Fig.3 Correlation analysis results of two samples

由图3 可知,真正父子节点的特征矢量相关程度均表现为强相关或极强相关［2］,且样本的数据长度越大,相关性普遍越高。即使相关系数较小时,真正父节点与其次可能的父节点之间相关系数差值仍大于0.2,区分效果显著,不会导致分支节点上下与并行关系的误判。

具体地,针对图3（a）中相关系数较小的分支单元9_1（即节点9 的第1 个分支节点,以下形式类同）,由初始的AB1判断其可能的父节点包括节点1、1_2、1_1。利用节点功率相关性的辨识流程如下。首先,对上述4 个节点的功率曲线进行频域滤波,获取高频功率曲线。然后,通过提取节点9_1 较其他所有待识别节点（即节点111_1 至节点171_1）变化更显著的特征点,构建节点9_1 的特征矢量,特征提取的过程如附录B 图B2（a）所示。最后,对节点的特征矢量进行相关性分析。经计算,节点9_1 与真正的父节点1_1、其次可能的父节点1_2、节点1 的相关系数分别为0.67、0.12、-0.07,节点的特征矢量如附录B 图B2（b）所示。此外,节点1_1 与9_1 功率序列的相减,保证了9_1 的兄弟节点9_2 与1_1 的强相关性,其相关系数为0.97,说明辨识上下与并行关系效果明显。

另外,因对分支节点任意时刻的三相功率进行了累加,遮蔽了节点间的相序信息。下一步,借助辨识父子节点的方法分析邻层节点的相序关系,附录A 图A5 给出了下游分支相节点与上游相节点之间的相关系数,其中横坐标中的42 个相节点分别对应于图3 中14 个分支单元的相节点,蓝色的点代表所分析相节点与其真实父节点之间的相关系数,其余两个颜色的点表示与其他两个异相节点的相关系数。从细节来看,尽管节点1_1 和9_1 间存在3 个分散用户,但相序间的相关系数均大于0.75,且均远大于与其他两相的相关系数,说明所提方法能够有效地辨识邻层分支节点的相序关系。

最终的邻接矩阵AB刻画了网络分支的上下、并行、相序关系,通过将其与系统网络拓扑比对分析,验证了所提方法辨识分支节点层次关系的有效性。15%、35%两种能量渗透率下的计算结果如附录A图A6 和图A7 所示。对比上述结果和前述分析可知,无论是在低比例还是中或高比例渗透的情况下,所提方法均能够通过初始化减轻冗余信息的干扰,并借助功率序列的耦合相关性准确地辨识出分支节点的层次关系,并且数据长度越大,辨识效果越显著。

2）用户区段定位结果

在某种误差场景中,由分支节点的层次关系判定线路区段总数为45。同时,鉴于在时段Y中消耗总功率最小的用户为U71,在此基础上利用式（16）计算功率阈值δ并筛除无用户连接的7 条线路区段,即区段1a、1b、1c、1_1a 至9a、1_2b 至111b、1_2c至111c、111_1a 至124a,之后建立其他38 条线路区段的功率矩阵PL。汇集86 个用户的有功功率时间序列,构建用户节点的功率矩阵PC。将上述两个功率矩阵用于用户的区段定位,流程如下。首先,分别将线路区段和用户节点作为父节点和子节点,建立父子节点层次辨识模型并进行误差处理,近似计算导线损耗后,将0.5%的测量误差内嵌在父子节点的量测功率矩阵PM中,以获得量测功率矩阵PME。然后,采用SVD 对误差处理后的矩阵PME进行降维,并对124 个奇异值中最小的38 个奇异值对应的特征向量进行反变换,从而求解约束矩阵J。接着,对约束矩阵进行回归分析,通过求解回归矩阵Z,实现用户所属区段的定位。最后,根据矩阵Z的结果,考虑被筛除的7 条线路区段,构建用户节点关联矩阵AC,以反映用户节点邻接的分支相节点,回归与关联矩阵如附录B 图B3 所示。例如,在矩阵AC中,U3 和1_1c 对应的元素为1,说明相节点1_1c 为用户U3 的邻接节点,即U3 连接在节点1_1 与节点9 之间的c 相线路上。

在AC的基础上,结合分支节点的邻接矩阵AB并通过矩阵映射,求取拓扑的邻接矩阵A,如附录B图B4 所示。为直观展现节点的拓扑关系,附录B 图B5 给出了分支单元与用户电能表的可视化结果。对求解的拓扑邻接矩阵A与真实的拓扑邻接矩阵对比,验证了所提方法的有效性。下一步,通过计算拓扑邻接矩阵中正确识别的节点数与节点总数的比值,反映拓扑辨识的准确率。

4.3 对比分析

在已有拓扑辨识方法中,对分支节点层次关系的辨识多采用载波形式的特征信号［5-6］,难以实现与数据分析方法的对比。由于误差为2.5%时,所提方法仍可准确地辨识分支节点的层次关系,为进一步体现方法优越性,假设分支节点的层次关系已知,比较不同方法对用户区段定位的性能。为此,将本文方法与传统电压相关性方法［9］以及文献［27］所用的负荷变化相关性方法进行比较。其中,电压相关性是基于电压曲线相似性确定用户所邻接的分支节点,通过比较电压梯度识别用户的区段位置；负荷变化相关性通过分析线路区段与用户负荷变化的相关性,辨识用户的区段信息,结果如表1 所示。

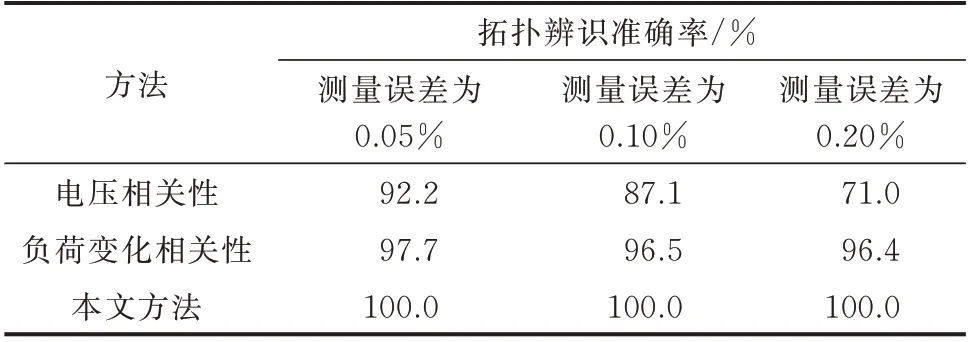
表1 不同方法的辨识准确率Table 1 Identification accuracy of different methods

由于电压幅值的误差精度通常不超过0.5%,表1 给出了7 d 样本,渗透率为8%,测量误差为0.05%、0.10%、0.20%,误差分布场景数量为100 的比较结果。可以看出,电压相关性的准确率随误差的增加而降低,当误差较低时,由于可再生能源的并网,容易导致用户区段信息的误判,造成拓扑辨识准确率不高的问题；负荷变化相关性对误差具有较高的误差容忍度,但受限于数据长度,其辨识率总体为97%；本文方法对误差噪声具有更好的鲁棒性且能适用于低压有源配电网,在该算例中,对用户区段定位的准确率均达到100%,说明在有限的量测数据下,本文所提方法在拓扑辨识方面具有一定的优势。

4.4 误差影响分析

针对8%、15%、35%这3 种渗透比例的能量渗透率,分别对7、15 d 的数据样本联合测试并进行误差分析。在考虑仪表更新率、延时偏差的同时,将分支与用户节点处有功电能表的计量误差预设至最大误差的两倍,即4.0%（3σ=0.04）,对每种误差均设置100 次误差分布场景,结果如表2 所示。表中,0.2、0.5、1.0、2.0、2.5、3.0、3.5、4.0 分别表示电能表的计量误差分别为0.2%、0.5%、1.0%、2.0%、2.5%、3.0%、3.5%、4.0%。

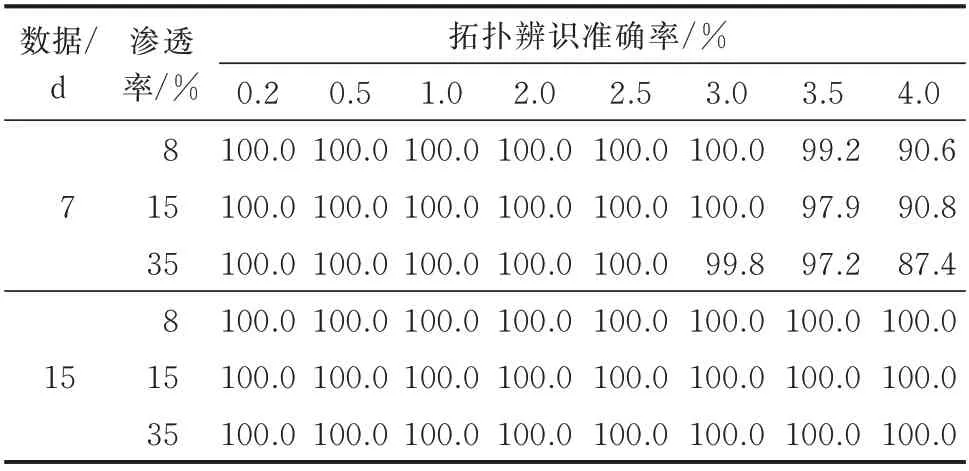
表2 不同情况下的拓扑辨识准确率比较Table 2 Comparison of topology identification accuracy in different cases

可见,在引入2.5%以内测量误差的情况下,对2 类样本的辨识准确率均达到了100%；当误差大于2.5%时,7 d 样本的辨识率相对低一些,结果随着误差的增加而下降。此外,随着能量渗透率的增加,同一误差下的辨识率略有下降,但不会大幅度降低辨识结果的准确性,表明基于功率数据能更好地对低压有源配电网的拓扑进行辨识。随着数据长度的增加,针对一定的延时偏差和4%范围内的计量误差,方法在精度方面的优势更为明显。这说明高比例可再生能源并网时,所提方法能够准确地辨识分支节点的层次关系、实现用户的区段定位,且对测量误差具有较高的容忍度。文献［26］规定有功电能表的测量误差在2%以内,因此,在该技术规范内本文方法将能够利用有限的数据集识别物理拓扑。这是因为上述方法的数学本质是借助数据分析算法,分析功率序列的耦合相关与逻辑加和关系。当存在功率倒送时,并不会改变节点功率间固有的关系,对于不同比例的可再生能源渗透率具有适用性。

5 结语

面向新型配电物联网架构,为辨识配电终端与分支单元的层次关系以及获取用户的区段信息,提出了一种基于分支有功功率的低压有源配电网拓扑辨识方法,得出如下结论:

1）通过求解图的邻接矩阵分析节点间的连接关系,可以简化拓扑辨识问题的求解。

2）通过挖掘上下游分支节点功率序列的耦合相关性,准确获取分支节点的上下与并行、相序关系。在此基础上,依据线路区段与用户之间的逻辑加和关系,有效实现用户所属区段的定位。

3）基于分支节点层次关系与用户区段定位结果,利用矩阵的联合映射准确构造出了低压有源配电网的拓扑邻接矩阵。当高比例可再生能源并网时,所提方法仍然能够在一定测量误差范围内,利用有限的数据集准确辨识拓扑,具有一定的普适性。

本文所提辨识方法仍存在一定的局限性和改进空间:一方面,未综合考虑其他灵活性资源、不确定延时与功率值的短时突变的影响。另一方面,区段定位算法是建立在无“零电量”用户的假设下进行的,“零电量”用户在一定程度上会影响辨识的准确率。下一步,在考虑风电、储能、电动汽车等因素的同时,融合其他有限的量测数据实现“零电量”用户的关联,并结合实测数据对所提方法做进一步的改进和完善,以提高该算法的工程应用水平。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。