基于机器学习的煤系致密砂岩气储层分类研究<br/>——以鄂尔多斯盆地DJ区块为例

基于机器学习的煤系致密砂岩气储层分类研究
——以鄂尔多斯盆地DJ区块为例

2022-08-09要惠芳赵明坤

煤炭科学技术 2022年6期

要惠芳 ,赵明坤，陈强

(1.太原理工大学矿业工程学院，山西太原 030024；2.煤与煤系气地质山西省重点实验室，山西太原 030006；3.河南省煤炭地质勘察研究总院，河南郑州 450052)

0 引言

致密砂岩气资源量约占到全球非常规资源量的70%，是重要的接替能源[1]; 鄂尔多斯盆地作为我国主要的深部致密砂岩气产区，其上古生界石炭、二叠系储层是典型的以低、特低孔隙度和渗透率为特征的准连续型气藏，物性非均质性较强[2-4]。流动单元，又称岩石物理流动单元[5]、水动流动单元[6-7],是受沉积、成岩作用等因素控制的、以非均质性为特征的不同类型储集单元，而在相同类型单元内部岩石物理性质相似，流体渗流特征相似[8]，可近似为均质性的或可预测的[5,9]。因此，流动单元的合理分类是决定是否可以将低孔低渗储层物性的非均质问题简化为均质问题的关键。流动单元的划分主要有成因特征分类法及微观孔隙结构统计分析法2类。前者全部或部分考虑了沉积相、岩石相、成岩和构造作用等地质控制因素，具体表征参数包括矿物组分和粒度、成熟度及分选性等岩石学特征[10]，压实、胶结、溶蚀、破裂等成岩作用特征[6]，高分辨率层序及成因砂体组合、沉积微相及界面，隔层、夹层、沉积构造等沉积学特征[11]，断层及其封堵性等构造学特征[12]，划分方法有层对比及相叠加[10]、层次分析[13]、灰色关联[14]等。但该类方法对地质认识依赖大，效率低，可实现性较差。而微观孔隙结构法主要利用孔隙度、渗透率、孔喉半径等测试数据，通过流动层段指数(FZI)和孔喉半径R35等表征参数，基于测井数据采用多元线性回归[15]、聚类分析[16]、神经网络[17-19]、支持向量机等算法[20-21]等，划分不同类型的流动单元，进而在同类单元内，利用孔隙度与渗透率的良好相关性，建立相应的渗透率解释模型[22]。由于后者可以将厘米-米尺度的宏观测井参数与微米尺度的孔喉等微观结构、分类算法等多方面因素有机地结合起来，而且可将取心井成果推广至未取心井，预测性强，更有利于低孔渗气藏的高效分类和评价。因此，流动单元统计分类方法是目前应用最广泛的储层分类方法[23]，也是准确评价低孔渗储层物性参数，提高预测精度的重要途径。但是以往流动单元统计分类研究还存在一些不足，如数据集的规模较小，分类算法及模型单一等。各区块在长期勘探开发中积累了海量的数据，包括数值型(孔渗测试数据、压汞、测井等)和类别型或名称型数据(岩心观察、薄片、X射线衍射和扫描电镜等反映的岩石相和成岩相特征)等。近年来，基于数据驱动的机器学习技术发展迅速[24]，为充分利用上述数据，实现流动单元成因及微观孔隙结构特征的综合分类，加深对致密砂岩储层的认识，提供了一个极具潜力的工具。基于此，研究将利用鄂尔多斯DJ区块1 880块岩心柱塞孔渗分析及33组压汞分析资料，基于概率累积分布函数曲线变化特征及孔-渗相关性，优选流动单元分类方案；在此基础上，结合734组宏观岩石相等类别型及数值型测井数据，尝试建立无监督、有监督2类机器学习模型，并通过K均值聚类、决策树、朴素贝叶斯、随机森林、梯度提升树、支持向量机、深度学习7种分类模型的性能评估，探讨致密砂岩流动单元机器分类学习的可行性。

1 DJ区块致密砂岩储层特征

研究区位于鄂尔多斯盆地东部晋西挠褶带中南段(图1)，整体为一倾向NW的单斜构造,地层走向及主要构造轴向均呈NNE向；构造变形较弱，仅东部有古驿-窑渠背斜、薛关-峪口断层带等；主要储集层段位于含煤系地层内，为一套稳定地台构造背景上的浅海陆棚—三角洲-河流、湖泊充填沉积,包括本溪组，太原组、山西组和下石盒子组，埋深为1 500～2 500 m；发育有多套煤及煤线，且富含有机质的暗色泥岩，泥灰岩等优质烃源岩；上石盒子组发育一套稳定的厚度约100 m的湖相泥岩，盖层条件较好。本区块虽然从早白垩世以来持续抬升剥蚀，仍然保留了可观的致密气资源,呈现准连续分布、源外成藏、近源聚集的特征[3]；区内砂岩经历了压实压溶、不稳定组分溶蚀以及碳酸盐、硅质和黏土矿物胶结等多种成岩作用，现处于晚成岩阶段B期[26]。多类型、多期次、不同强度的成岩作用及其叠加对本区砂岩孔隙、裂隙的形成、保存以及破坏产生了极为复杂的影响。

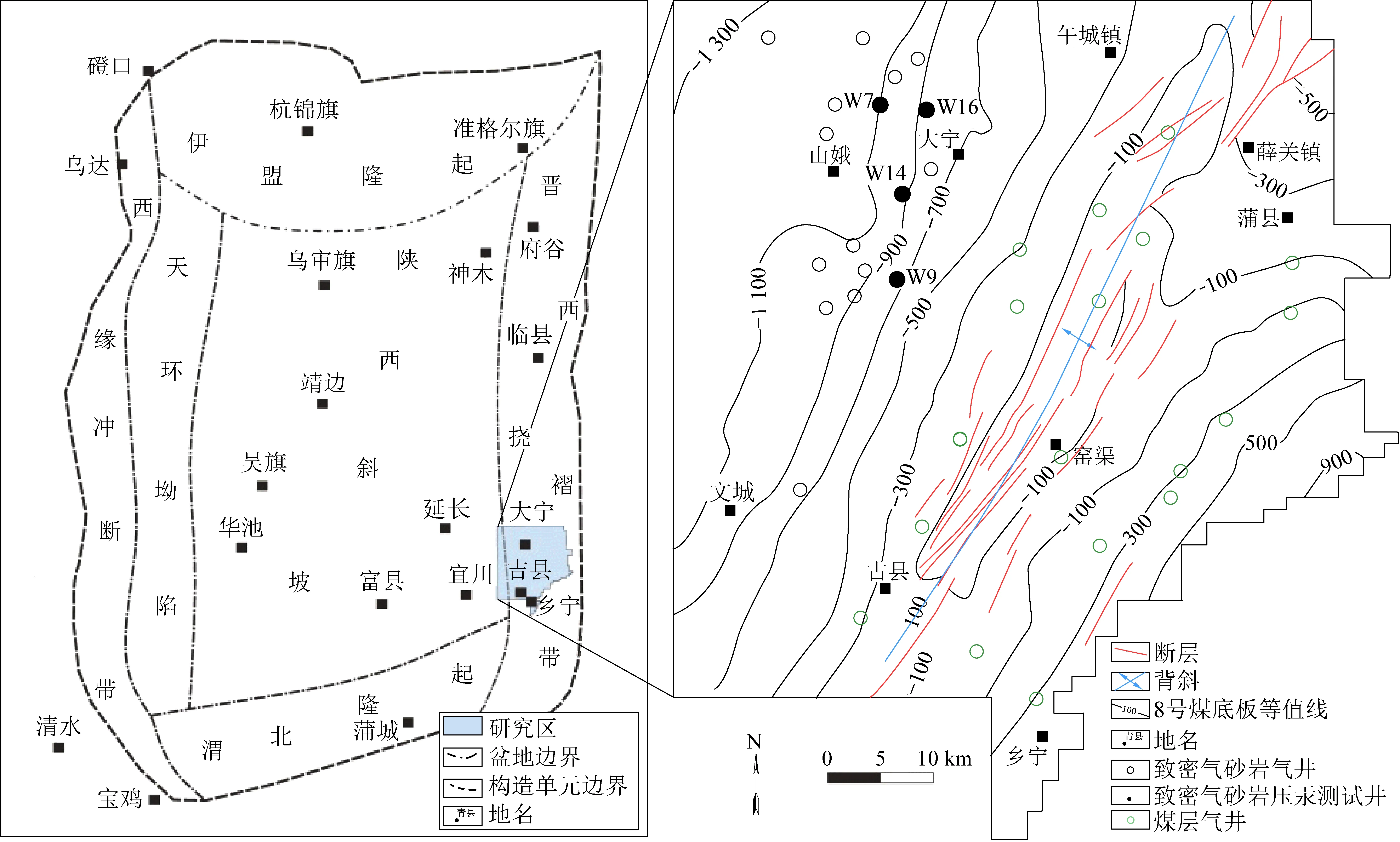
图1 研究区位置及构造纲要图Fig.1 Location and structure outline map of DJ Block

1.1 致密砂岩储层岩石相特征

已有研究表明[25]，DJ区块砂岩碎屑成分以石英或岩屑为主，长石含量低，通常不超过4%；岩屑组分主要为沉积岩,次为变质岩和火成岩。填隙物质量分数为6%～37%，杂基(以泥质为主)含量一般低于胶结物；在结构特征方面，粒径以中粒居多，粗粒及细粒也有一定的分布；磨圆度以次圆-次棱角状为主，分选好-差；成分成熟度、磨圆度及分选性呈现随地层由老至新逐渐变差的趋势。

根据碎屑组分和粒度，本区砂岩可分8种岩石相类型(图2)。其中，图2a为DJ4-6井山2段粗粒石英砂岩，孔隙较发育，钙质胶结为主，石英次生加大明显；岩屑含燧石、硅质岩、酸性火山岩；图2b为DJ5-8-15井山2段中粒石英砂岩，孔隙发育一般，硅质胶结。岩屑以燧石、硅质岩为主，含少量碳酸盐岩；图2c为DJ4-6井山1段粗粒岩屑石英砂岩，孔隙欠发育，硅质-泥质胶结为主，石英次生加大边明显。主要岩屑为变质岩、泥板岩及少量白云母，碳酸盐岩；图2d为DJ6-5井盒8段中粒岩屑石英砂岩，孔隙发育，粒间与粒内溶蚀孔隙为主，含长石及碳酸盐岩等刚性易溶岩屑；图2e为DJ7井盒8段粗粒岩屑砂岩，孔隙较发育，泥质胶结为主，局部石英有次生加大；岩屑为变质石英岩、碳酸盐岩、燧石、酸性火山岩。图2f为DJ7井盒8段中粒岩屑砂岩，泥质胶结，孔隙较发育；岩屑包括泥板岩、燧石、变质石英岩，碳酸盐岩、酸性火山岩；图2g为DJ5-8井盒8段细粒岩屑石英砂岩，孔隙较发育，硅质胶结为主；岩屑以硅质岩、燧石、酸性火山岩、碳酸盐岩为主；图2h为DJ6-8井盒8段细粒岩屑砂岩，孔隙欠发育，有较弱的粒间与粒内溶蚀孔隙，泥质胶结，溶蚀作用较弱；岩屑主要有泥板岩、片岩、白云母等软岩。

图2 DJ区块典型岩石相的铸体薄片Fig.2 Thin sections photomicrographs of typical lithofacies in DJ Block

1.2 微观孔、渗特征

根据岩心观察、薄片和X射线衍射、扫描电镜结果，本区砂岩孔隙类型主要为原生残余粒间孔及泥质杂基微孔、溶蚀粒间孔和粒内孔、铸模孔、晶间孔和微裂隙等次生孔隙；岩心孔渗资料统计分析表明，区内砂岩孔隙度为0.60%～19.88%，中值5.85%，渗透率(0.000 4～244)×10-3μm2，中值0.131×10-3μm2；DJ区块虽然以特低孔渗储层为主，但部分层段发育有大孔喉及微裂缝，渗透率有所改善。

DJ7等关键井的33个岩心柱塞压汞数据表明，储集岩中值压力为1.0～5.5 MPa，平均值4.4 MPa，喉道系数5.272～12.180，中值为9.35；喉道分选系数1.414～5.109，中值2.56；结构系数0.122～108.100，中值0.28；偏度0.028～2.530，平均值1.51；平均孔喉半径为0.076～11.115 μm，中值0.28 μm；R35孔喉半径为0.016～10.036 μm,中值为0.2 μm，具有显著的小孔径、窄喉道的孔隙结构特征。根据上述特征可划分3种类型(图3a)，第I类峰值孔径为8.0～11.9 μm，第Ⅱ类0.12～1.26 μm，第III类0.012～0.032 μm；相对应的35%进汞饱和度毛管压力约为0.9 MPa(图3b)，20 MPa(图3c)和80 MPa(图3d)。

图3 典型孔径特征分布及其压汞曲线Fig.3 Distribution characteristics chart of three typical throat size and mercury injection capillary pressure curves

整体来看，主要受宏观岩石相、沉积相、成岩相等多种地质因素的控制，本区砂岩储集层的孔渗特征非均质性极强。

2 流动单元分类

2.1 流动单元划分方法及标准

AMAEFULE等[7]提出了采用孔隙度和渗透率实现流动单元分类的FZI法，FZI值计算方法如式(1)—式(3)所示：

(1)

(2)

FZI=RQI/φz

(3)

式中:RQI为储层品质指数，μm;FZI为流动层段指数；k为渗透率,10-3μm2;φe为有效孔隙度，%;φz为标准化孔隙度，%。

此外，PITTMAN等[26]认为压汞曲线上进汞饱和度达35%时的孔隙半径R35能够反映流体流动状态,因此可用其来划分流动单元；利用孔隙度和渗透率计算孔喉半径R35值的方法见式(4)[27],即

lgR35=0.523lgφ-0.565lgk-0.255

(4)

式中:φ为孔隙度，%。

为更好地反映研究区实际孔渗特征，将33组R35与孔隙度、渗透率实测值作了二元非线性回归，回归方程见式(5)，R2可达0.96。

lgR35=0.650 3lgk-1.019 2lgφ+0.105 2

(5)

因此，利用式(3)和式(5)对研究区1 880组岩心数据分别计算了FZI和R35，在此基础上，进一步计算了lg FZI和R35的概率累积分布函数(Cumulative density Function)(图4)。

按照文献[16]中的方法，基于lg FZI和R35概率累积分布函数曲线的斜率变化特征，划分了3类流动单元，如图4和表1所示。

表1 DJ区块储层流动单元分类Table 1 Classification scheme of reservoir flow units

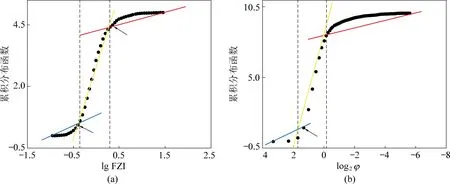
图4 Lg FZI及R35指数概率累积分布函数散点图Fig.4 Cumulative density function plots to obtain optimal number of lg FZI and R35 flow units

图4中黑色箭头所指的位置即累积密度分布函数曲线斜率的突变点。无论是lg FZI还是R35法，除第Ⅱ类单元外，其他2类单元内部还可见小的斜率变化，仍可细分；但由于在所有样本中，第Ⅱ类单元中的样本占比(>50%)远大于其他2类(<16%)，如果再将Ⅰ类和Ⅲ类细分，其样本数量会更少。此外，在后续机器学习前还需做数据清洗工作，数据集之中的样本数还将进一步减少。因此，本次对Ⅰ，Ⅲ类单元划分标准做了部分粗化处理。

2.2 流动单元分类方案优选

根据表2中流动单元划分标准，将3类单元中的所有样本投影到φ-lgk坐标系，如图5和图6所示。渗透率的孔隙度一元回归模型见表2。通过对比可以发现：① 各类流动单元内孔隙度与渗透率的相关性显著提升，仅有一个单元的R2小于0.5，其余为0.68～0.81(表2)。说明FZI和R35两种流动单元分类法均能反映微观孔隙结构的变化，且同一流动单元内的样本具有相近的孔喉特征；② 在同一单元内，随着孔隙体积比的增加，渗透率呈幂指数增大；③ 相同孔隙体积条件下，FZI和R35值越大，孔喉半径和渗透率越大，具有I类>II类>III类单元的变化规律；④ FZI和R35两种分类方案的主要差别在于第I类单元，R35划分结果中孔渗相关度仅为0.47，相对于FZI的0.81明显变差。因此，本次流动单元分类最终采用了基于流动层段指数FZI的划分方案。

图5 lg FZI值划分的流动单元孔、渗分布特征Fig.5 Three flow units identified by lg FZI indicator in relation to porosity and permeability

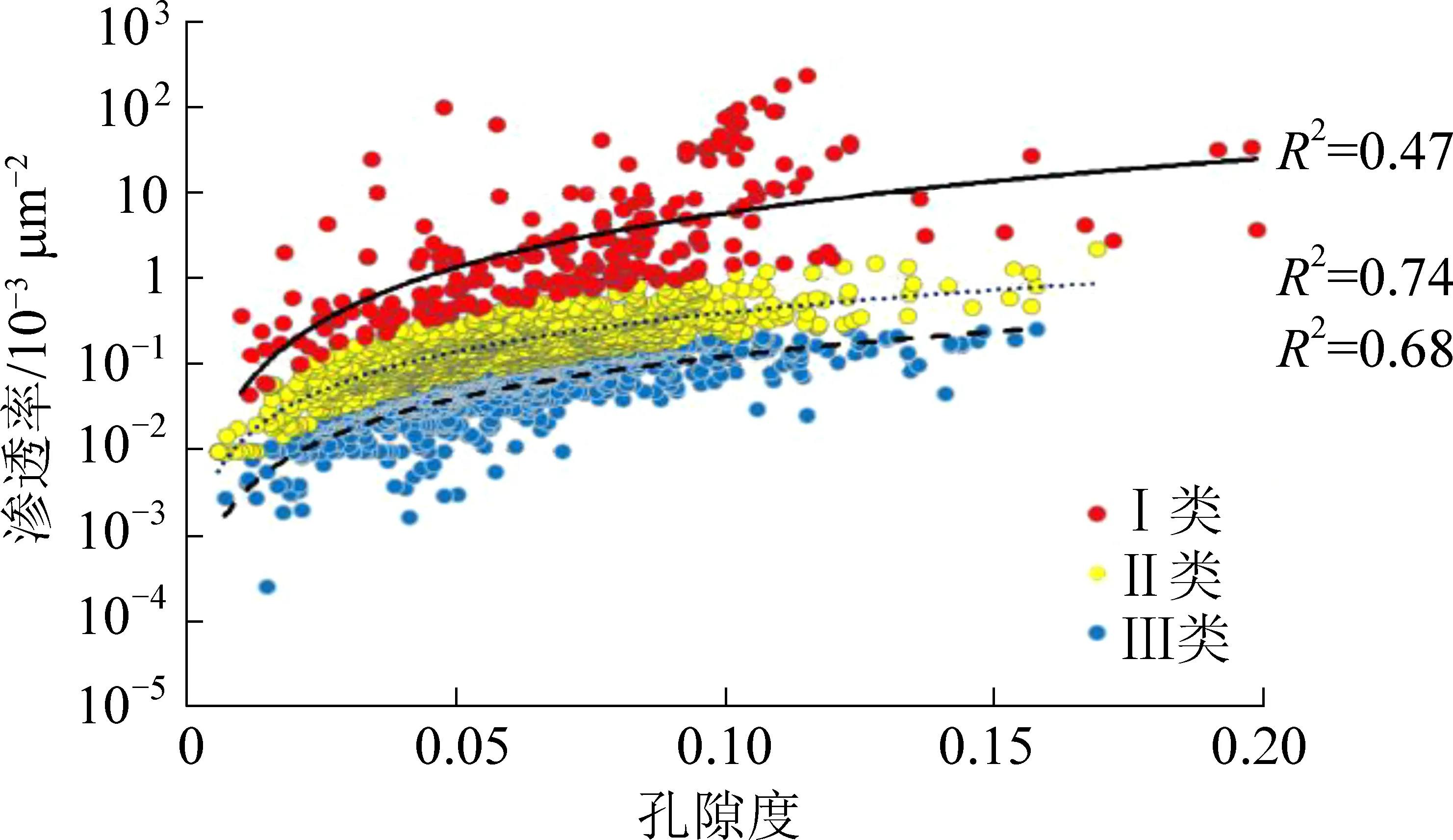
图6 R35值划分的3类流动单元的孔、渗分布特征Fig.6 Three flow units identified by R35 indicator in relation to porosity and permeability

表2 DJ区块3类流动单元渗透率解释模型Table 2 Permeability interpretation models of 3 flow units in DJ Block

综上，合理的流动单元划分方案可以改善微观孔隙结构的均质性问题，提高孔隙度和渗透率的相关度。这样，当砂岩样所属流体单元判别正确时，渗透率的预测精度将会大幅提高。

3 机器学习分类建模及效果

鉴于大多数井不取心，仅有测井和录井资料。因此，如何以测井、录井数据为媒介，将岩心测试成果统计分析确定的流动单元的分类成果，推广至未取心井，实现流动单元的高精度分类，是本次流动单元分类机器学习重点解决的问题。

3.1 机器学习数据集及数据处理

3.1.1初始数据集

共收集到46井1 880组的岩心孔隙度、渗透率测试数据以及少量的岩心观察、薄片、岩电测试分析等资料；但相对应且有完整测、录井信息的样本较少，最终可用于机器学习的仅有24井808个样本。

3.1.2数据属性

测井选取了井径(CAL)、补偿中子(CNL)、自然伽玛(GR)、自然电位(SP)、声波时差(AC)、补偿密度(DEN)、视电阻率(Ra，8 inch感应电阻率)、岩性密度(PE)、测井孔隙度(POR)等9种参数属性；此外，通过计算样点埋深以上岩石的垂向静压力构建了表征应力差异的垂向应力属性；利用各层段沉积的地质年代(时间)构建了年代属性，具体属性值有盒7，盒8，山1，山2，太原，本溪共6个；利用录井资料构建了岩石相属性，具体属性值有粗粒石英砂岩、中粒石英砂岩、粗粒岩屑石英砂岩、中粒岩屑石英砂岩、粗粒岩屑砂岩、中粒岩屑砂岩、细粒岩屑砂岩等7个。以上12个属性中，岩石相、年代属性为类别型数据，其他均为数值型。

3.1.3分类标签

按照表1中FZI指数的分类标准，将lg FZI的2个特征值-0.35和0.2作为门槛，定义了3类流动单元，并对所有样本设定了相应的分类标签，作为输出变量，用于有监督学习的训练和测试。

3.1.4数据集处理

通过深度校正、环境校正和标准化等预处理，使测井数据在区内具有统一的刻度，并使系统误差减至最小。对电阻率做了对数处理，使其数据分布呈正态化；自然电位进行了泥岩基线校正；以井径增大率小于50%为门槛对数据进行了筛选，筛选后总样本数减少至24井734组。此外，针对部分异常值和噪音做了零均方差(Z-score)标准化处理；针对不同属性值数据范围差异大的问题，基于不同算法要求在学习过程中做了线性或非线性归一化处理。

3.2 分类算法

机器学习模式可分为2类：无监督与有监督学习。研究的重心是测试有监督学习算法，以期对测井、岩石相等数据(输入)和流动单元类型(输出)之间的关系进行泛化和评估，最终实现分类模型优选。因此，只采用K均值聚类算法进行了无监督学习试验，而测试的有监督学习算法共5种，包括朴素贝叶斯、决策树、支持向量机、深度学习和集成学习算法(随机森林、梯度提升树)。6种机器学习算法原理简述如下：①K均值聚类(K-means Clustering，KC)，是一种无监督学习方法，需要给定簇的个数，找出各簇的质心，将与各质心距离相近的数据点聚集成簇，实现分类；② 朴素贝叶斯(Naive Bayesian，NB)，是一种统计学方法，通过对相互独立的多个输入变量，应用贝叶斯理论计算各个类别的概率，选取最大概率对应的类别作为分类结果；③ 决策树(Decision Trees，DT)，是一种信息论方法，通过信息熵构建纯的子集，对目标变量影响最显著的将在树的根或近根层次；④ 支持向量机(Support Vector Machine，SVM)，采用数学最优化理论，通过构建多维的超平面形成多个界面进行分类；⑤ 深度学习(Deep Learning，DL)，通过模拟神经元的工作方式，建立具多隐层结构且有反馈的网络来连接输入和输出，从而实现分类；⑥ 集成学习，一种“元学习”方法，通常由多个不同的独立模型，利用集体智慧如投票的方式，综合成一个最优的模型。该类算法非常适合噪声数据、离群点存在的数据集，本次测试的随机森林(Random Forest，RF)和梯度提升树(Gradient Tree Boosting)均为以决策树为基础模型的集成学习类算法。

本次机器学习分类的所有算法均在Rapidminer Studio数据挖掘平台上实现。

3.3 训练及测试数据集

通过以上方式处理后的数据集中共包含734组样本(24井)，其中I类样本111个，Ⅱ类496个，Ⅲ类127个；各分类样本数失衡，为提高后续建模的可信度，须作均化处理[24]。为保证有相同的数据分布特征，按二次分层抽样(Stratified Sampling)方式对II类数据进行了1/3比例抽稀，并分别与I类和III类样本合并，形成3个数据子集分别进行建模。每个子集内3类样本数量一致，均为111-165-127，总样本数量为503。每个子集均按50%～90%的比例抽样训练，剩余样本作为测试集进行验证和评估；最终的模型性能指标以3个子集的等权重之和计算，再进行评估。

针对不同的算法特性，本次机器学习的训练和测试选择了不同的属性集合：K均值聚类、深度学习、支持向量机等全部采用纯数值型数据，具体包括CNL、GR、SP、AC、DEN、Ra、PE、垂向应力等8种；朴素贝叶斯、决策树、随机森林和梯度提升树采用数值型和类别型的混合型数据；包括年代、岩石相、POR、CNL、GR、SP、Ra、垂向应力等8种。

3.4 建模参数优选

每种算法均需要与特定数据集与方法本身匹配的建模参数，如决策树的树个数、支持向量机的学习速率等。上述参数如用人工进行优选，效率低，客观性难以保证。为此，采用参数区间及其步长设定-训练-建模-测试-性能评估的交互验证方法，其优点在于，每一组参数的改变均可由计算机自动实现训练、建模和测试，并获得其所建模型的分类精度、召回率和平衡分数f1值等。由于f1能综合反映分类精度和召回率的变化[24]，相对更全面，因此，可以通过f1箱形图的变化特征对各算法的建模参数及其组合进行分析和优选，以保证各算法均能实现最佳分类。

不同算法对于建模参数的敏感度不同，f1离散度越高就越敏感[28]。图7为6种有监督学习算法的不同建模参数组合f1得分值箱形图，在图7中，朴素贝叶斯f1分布最为集中，深度学习和支持向量机f1离散度最高，以决策树为基础的3种算法介于两者之间，说明深度学习和支持向量机2种算法对建模参数要求是最高的；此外，二者虽然最高和最低得分基本相同，但f1的中位数差异较大，深度学习为78.8%，而支持向量机仅73.5%，说明后者只有少数参数组合有较好的分类表现，算法对参数依赖性强，稳定性较差。

图7 不同算法建模参数组合的验证f1得分箱形图Fig.7 Boxplots of f1-score obtained from cross validation performed over different parameter sets of each algorithm

通过上述方法，可以得到每种算法的最优参数组合。以梯度提升树模型为例，其最优参数为：树个数：100；可再生性：真实；本地随机种子数：1992；最大深度： 10；学习率：0.02；分布形式：多模态。

3.5 模型性能评估及模型优选

3.5.1有监督与无监督学习模型

图8为无监督学习K均值聚类方法与其他5种有监督学习的最终分类效果对比图，与图5相同，红色样点代表Ⅰ类流动单元砂岩，黄色为Ⅱ类，蓝色为Ⅲ类。可见，有或无监督学习这2类机器学习模型的样点分布特征大相径庭， 5种有监督学习算法的样点分布与图5相近，而K均值聚类模型结果与FZI分类基本不相关。这一现象说明同样基于数据驱动，以消极学习为特征的K均值聚类只有在数据本身与分类目标期望契合的特定情况下，才可能实现理想分类；而以深度学习为代表的积极学习算法，在类标签的约束下，对隐含规则或关系的泛化能力更强，知识挖掘能力更高。因此，如若应用无监督的机器学习算法对流动单元进行分类，训练测试数据集的构建至关重要；而有监督的、积极的学习方法不需要对数据集进行针对性处理，学习门槛低，效率更高。

图8 不同机器学习算法分类结果对比Fig.8 Classification results of different machine learning algorithms

3.5.2有监督学习模型优选

该类模型的整体表现较好，f1最高值均超过了72%(图7)，可以对流动单元进行有效分类。另外，从中值分布特征来看，朴素贝叶斯最低仅为71%；深度学习、梯度提升树和随机森林2类集成学习算法的表现较好，中值分别为78.8%、79.0%和77.8%，接近80%，而朴素贝叶斯、决策树和支持向量机较低，为70%～74%。

综合f1分布特征(图7)和分类效果(图8)，本次机器学习最终确定的最优模型有2个：一个是基于数值型数据集的深度学习模型，另一个是面向数值和类别型混合数据的梯度提升树模型，其f1平均得分值分别为82.63%和85.56%，其性能指标详见表3。

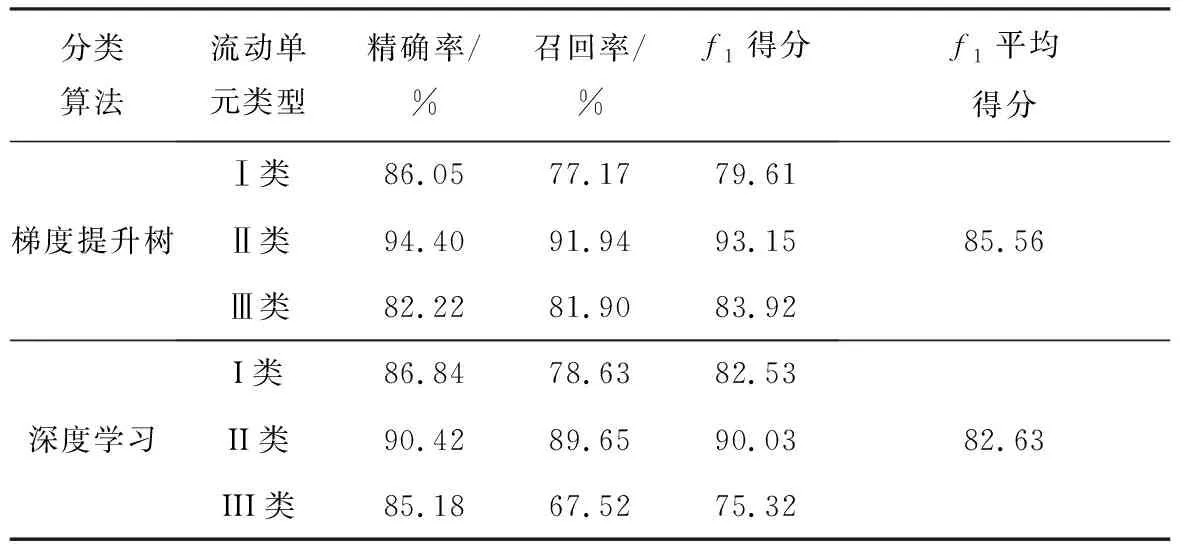
表3 梯度提升树和深度学习分类模型性能对比Table 3 Classification matrices obtained with prediction over training set using GTB and DL algorithms

可见，在DJ区块，采用不同的数据类型和与之匹配的机器学习算法，可以构建出准确度和可靠性相近的不同机器学习模型。因此，能够实现流动单元高效合理分类的机器学习模型并不是唯一的。

对于工程应用来说，可以基于井径、补偿中子、自然伽玛、自然电位、声波时差、补偿密度、视电阻率、岩性密度等表征岩性、物性和流体性质的测井参数，通过构建以深度学习为代表的数值型机器学习

模型，实现流体单元的准确分类，进而提高渗透率的测井解释精度。虽然这一类模型难以解读其地质含义，但是方法健壮性好，分类预测精度高，既能处理高度非线性问题，又有极强的反馈能力[28]，是高效完成现场准确预测任务的最佳选择。

但对于流体单元的成因特征等基础地质研究来说，由于其采用的地质语言均为类别型，如不同类型砂岩的形成年代、岩石相、沉积微相、成岩相等，很难转换为数值型数据加以量化表征，深度学习、支持向量机等数值类机器学习算法无法处理。能够对上述信息进行处理的只有朴素贝叶斯、决策树和以其为基础的梯度提升树、随机森林等集成学习模型，而且模型结果兼具可解读性[29]。虽然本次研究仅考虑了岩石相和年代特征，但是DJ区块梯度提升树学习模型研究初步表明(图9)：排在前13位的建模影响因子中(影响因子总和为81.8%)，测井孔隙度等6种数值型属性贡献率之和为45.1%，粗粒石英砂岩等7种岩石相类别属性为36.7%，说明二者影响力相当，岩石相同样对最终模型的构建有显著影响。同时也可以看到，岩石相的属性变化对本区砂岩储层渗流特性的影响程度明显高于年代属性(未进入前13位)，控制作用更明显。如果能进一步考虑成岩相、沉积微相等其他类似岩石相的地质信息，建立更完善的数据集，利用已有的FZI流体单元分类结果，完成训练、建模和测试，就能通过解读最优模型泛化产生的具体分类指标，挖掘其关联关系和分类规则，归纳分析不同相及其耦合对流体单元分类的影响程度，从而形成关于研究区砂岩渗流特性成因的地质控制要素及其耦合关系的新认识。