特厚煤层回采巷道塑性区形态特征及演化规律研究
2022-08-09孙光中
镐 振,孙光中
(1.河南工程学院 资源与安全工程学院,河南 郑州 451191;2.河南理工大学 深井瓦斯抽采与围岩控制技术国家地方联合工程实验室,河南 焦作 454003;3.河南工程学院 矿山安全与绿色开采研究院,河南 郑州 451191)
0 引 言
随着我国矿井开采深度和强度的不断增加,由复杂应力条件下造成的巷道围岩破坏愈加严重,由此造成的巷道大变形、冒顶、冲击破坏等灾害事故频发,严重威胁着矿井的安全高效生产,特别是近几年,在河南义马、甘肃华亭、陕西彬长等矿区,已有十多个特厚煤层(煤层厚度8~50 m)回采巷道频繁发生严重冲击破坏和支护困难的问题[1-2]。大量现场实践和理论研究均表明,巷道围岩变形破坏的实质是巷道围岩塑性区的形成和扩展,巷道围岩的破坏模式和程度取决于塑性区的形态特征和尺寸大小。因此,研究巷道围岩变形破坏也就可以转化为研究巷道围岩塑性区的形态特征及演化规律[3]。
国内外学者对巷道围岩塑性区的研究开始于20世纪30年代。KASTNER等[4]研究了双向等压条件下圆形巷道塑性区形态,于学馥[5-7]认为巷道塑性破坏区是椭圆形的,并提出了“轴变论”的观点。董方庭等[8]提出了巷道围岩松动圈支护理论,认为围岩松动圈是围岩应力超过围岩强度时所产生的破坏区。随着煤炭开采深度的不断增加,有学者研究发现深部岩体会产生破坏区域和未破坏区域交替出现的现象,将其称为围岩分区裂化现象[9-10]。
20世纪80年代,马念杰[11]、侯朝炯[12]采用数值模拟方法分析非等压条件下巷道围岩塑性区特征,发现巷道围岩塑性区存在“*”形分布特征,并初步探讨了该塑性区形态出现的条件。赵志强[3]重新推导了非等压条件下圆形巷道围岩的塑性区边界方程,将计算得出的非均匀塑性区称为蝶形塑性区,并深入研究了塑性区的形态特征和分布规律。近年来,马念杰团队[13-15]经过不断的研究,将“蝶形塑性区理论”应用于巷道支护设计、瓦斯抽采钻孔布置等方面。
千秋矿位于河南义马煤田中部,并且频繁发生巷道冲击破坏,仅21141工作面回采期间就有24次冲击破坏事件发生在运输巷,占千秋矿统计事件总数的58.5%[16]。掌握厚煤层回采巷道塑性区形态特征及演化规律,可以为煤岩动力灾害防控、巷道支护设计等提供理论依据。基于此,笔者以千秋矿21141工作面运输巷为背景,研究特厚煤层回采巷道塑性区的形态特征及演化规律,为该条件下的巷道围岩破坏机理研究奠定基础。
1 工程概况
义马煤田是我国典型的冲击灾害多发区域,其典型特征是煤层上覆岩层为厚度几十至数百米的砾岩,成分以石英岩、石英砂岩为主。千秋矿主采二煤,平均厚度25.2 m,煤层平均倾角12°。二煤上方岩层依次为泥岩、砾岩、粉砂岩、细砂岩互层(厚度约205 m)以及砾岩(厚度约407 m)。
千秋矿21141工作面运输巷发生冲击破坏事故的次数最多。该工作面平均埋深为684 m,倾向长度和走向长度分别为130 m和1 484.7 m,直接底为泥岩(厚度6.2 m),基本底为细砂岩。21141工作面运输巷实际掘进时留有厚度约为2 m的底煤,为半圆拱形巷道,断面尺寸宽×高为6 317 mm×3 800 mm,采用锚网索喷+36U型钢马蹄形全封闭可缩性支架支护。采用放顶煤采煤法,自然垮落法管理顶板。
2 巷道围岩塑性区形成力学机制及其形态特征
2.1 巷道围岩塑性区形成力学机制
煤层开采会引起顶板垮落并造成围岩应力的重新分布,从而导致回采巷道围岩区域应力环境产生变化,使得巷道围岩最大主应力方向发生偏转,有时最大主应力与竖直方向会产生夹角,而位于采空区周边的回采巷道在上覆岩层传递的倾斜方向作用力影响下(图1),回采巷道围岩出现非均匀破坏[16-17]。
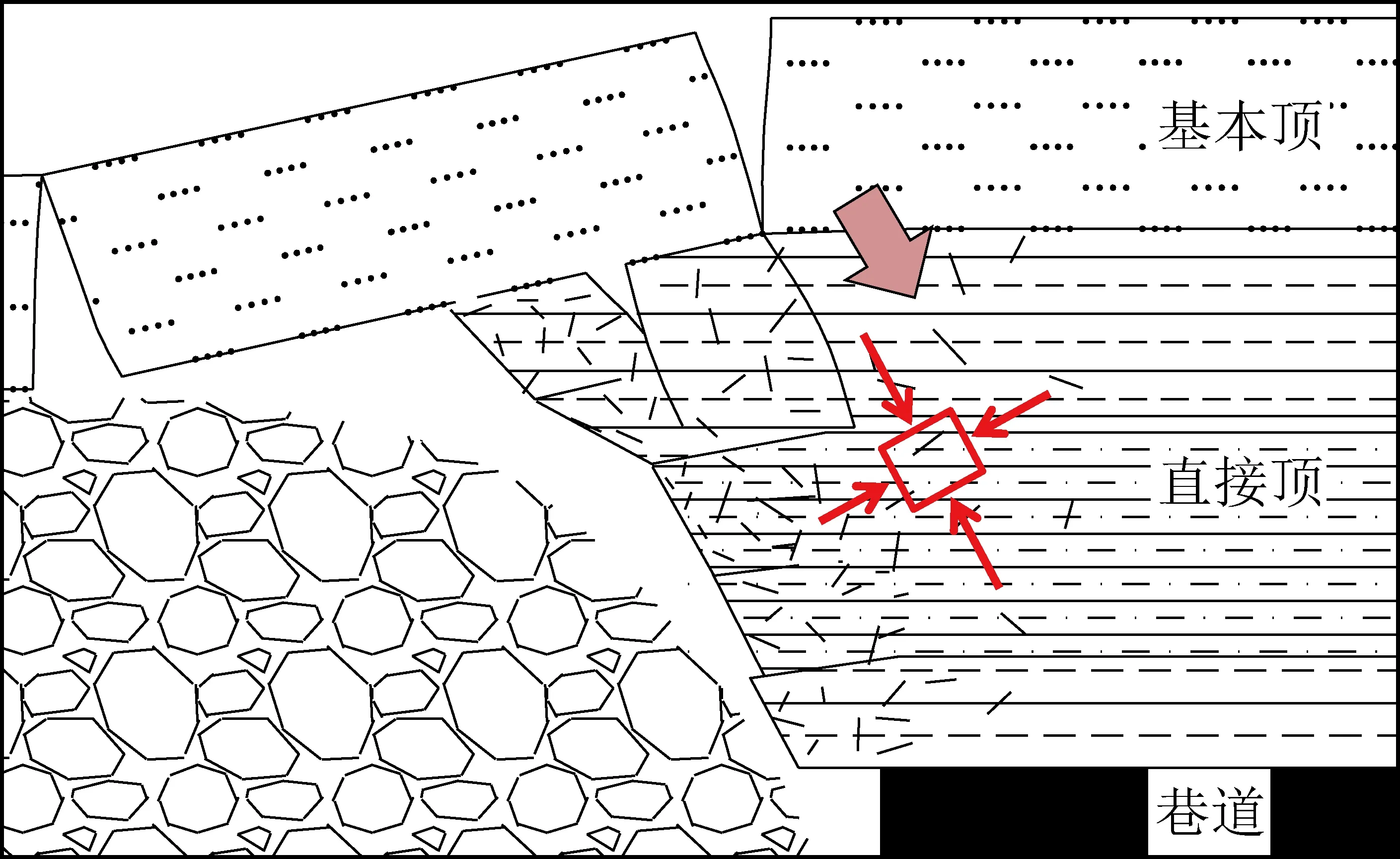
图1 回采巷道围岩应力环境Fig.1 Stress environment of mining roadway surrounding rock
处于非均质且各向异性岩体中的回采巷道,从巷道掘进到其服务的工作面回采结束,依次会受到掘进扰动、本工作面采动影响,有时还会受到邻近工作面开采形成的叠加应力场的作用。
为了分析特厚煤层回采巷道围岩塑性区的形态特征,在巷道所处区域取5倍巷道半径作为分离体,建立非等压应力场中圆形巷道围岩力学模型(图2)。分离体的边界条件为:内部几何边界为半径为a的圆形,P1与P3分别为作用在模型边界竖直方向和水平方向上的载荷。由于与原岩应力相比巷道支护力很小,所以内部应力边界忽略不计。

图2 非等压应力场中圆形巷道力学模型Fig.2 Mechanical model of circular roadway in inhomogeneous stress field
非等压应力场条件下圆形巷道围岩塑性区的边界方程[3,7]为:
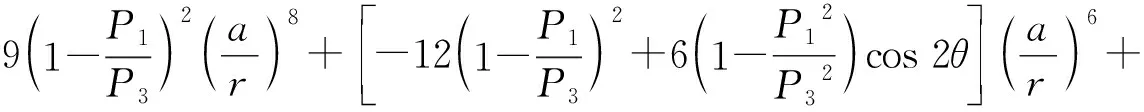
(1)
式中:C、φ分别为煤体的黏聚力与内摩擦角;r、θ分别为极坐标。
可以得出,巷道围岩的力学性质(C、φ)及其所处的应力环境(双向载荷比值P1/P3)决定了回采巷道塑性区边界范围。因此,在围岩力学性质一定的条件下,巷道围岩塑性区的形态特征及范围取决于巷道双向载荷比值P1/P3的大小。
2.2 巷道围岩塑性区形态特征
当围岩的力学性质相同时,在不同应力条件下,巷道围岩塑性区会呈现出不同的形态特征。在均质条件下,采用理论计算和数值模拟得出的圆形巷道围岩塑性区形态特征如图2所示。由图2可得,在相同双向载荷比值条件下,采用上述2种方法得出的圆形巷道围岩塑性区形态特征基本一致。当双向载荷比值P1/P3=1时,巷道围岩塑性区边界呈规则的圆形,如图3a所示。双向载荷比值P1/P3增加到1.5时,塑性区边界呈椭圆形,并且长轴和P3方向一致,如图3b所示。当双向载荷比值P1/P3达到2.5时,塑性区边界轮廓呈蝶形,塑性区最大尺寸在P1和P3夹角的平分线附近,如图3c所示。
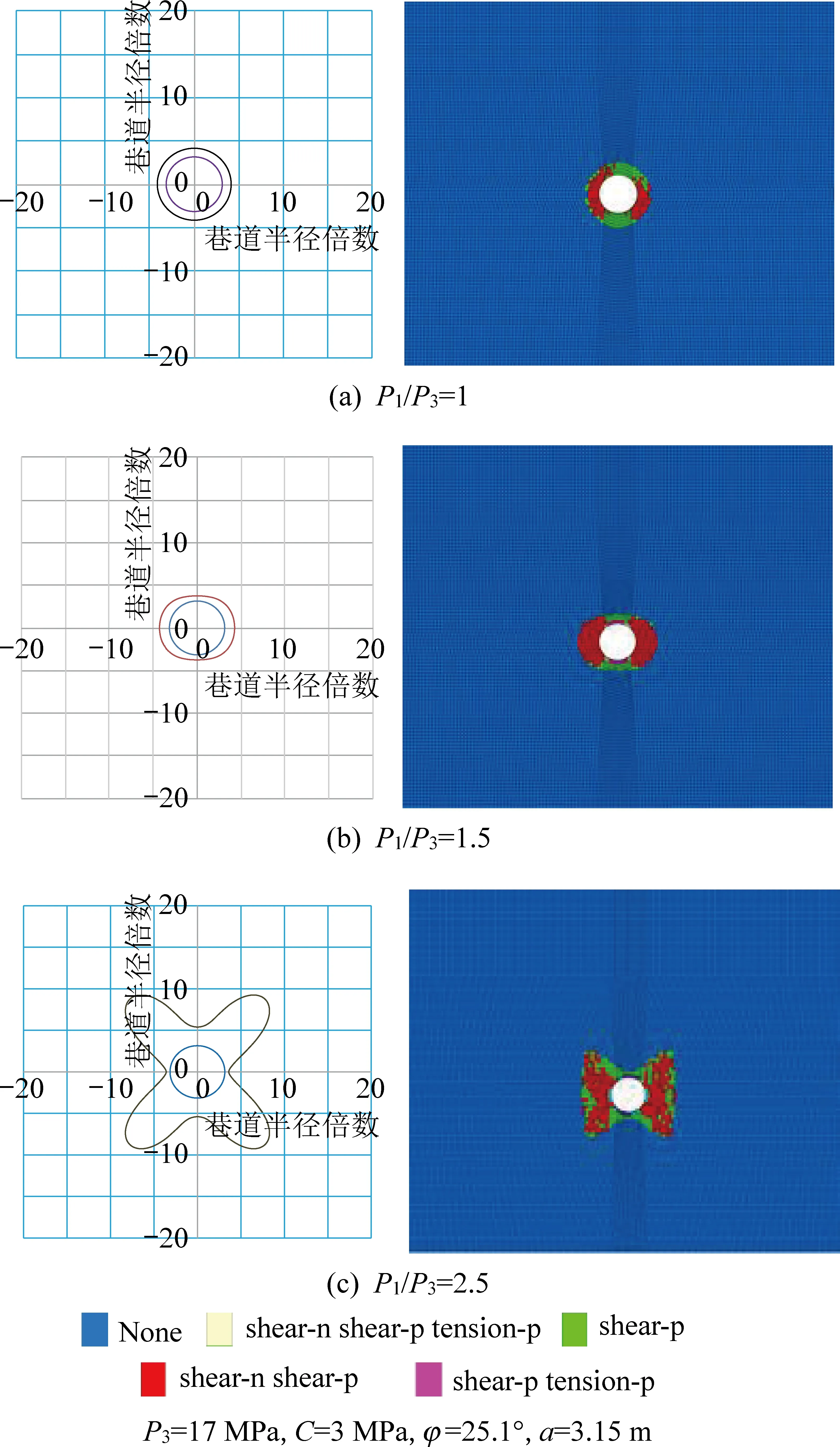
图3 不同双向载荷比值下均质圆形巷道围岩塑性 区理论计算和数值模拟形态特征Fig.3 Morphological feature of plastic zone of homogeneous circular roadway under different load ratios by theoretical calculation and numerical simulation
已有研究表明[3],蝶形塑性区对巷道围岩最大边界载荷的变化具有方向性。当巷道围岩最大边界载荷的方向发生变化时,塑性区蝶叶位置会随之偏转,如图4所示(图中红色为塑性区)。

图4 蝶形塑性区的方向性Fig.4 Directivity of butterfly shape plastic zone
3 特厚煤层回采巷道塑性区演化规律
3.1 模型的建立
结合千秋矿21141工作面煤层顶底板条件,建立大尺寸数值计算模型(图5),长×宽×高为1 000 m×1 550 m×950 m。模型中煤层倾角为12°,沿x轴和y轴正方向分别为工作面的倾向和推进方向。根据地应力测量结果,千秋矿最大水平主应力、最小水平主应力和垂直主应力分别为19.5、10.0、17.9 MPa[18];模型边界条件为:四周均固定水平方向位移,底面固定垂直和水平方向位移,上部为自由面,模型仅受重力作用。数值计算基于Mohr-Coulomb破坏准则。模拟煤层开采过程实行分步开挖,工作面开挖顺序依次为21101工作面、21121工作面、21181工作面、21201工作面和21141工作面(图6),岩石物理力学参数见表1。现场调研发现,在工作面推进400 m时,巷道冲击破坏事故较为严重,因此,在进行数值计算时,21141工作面开挖长度为400 m。

图5 数值计算模型Fig.5 Numerical calculation model

图6 工作面开挖顺序示意Fig.6 Numerical simulation on working face mining sequence
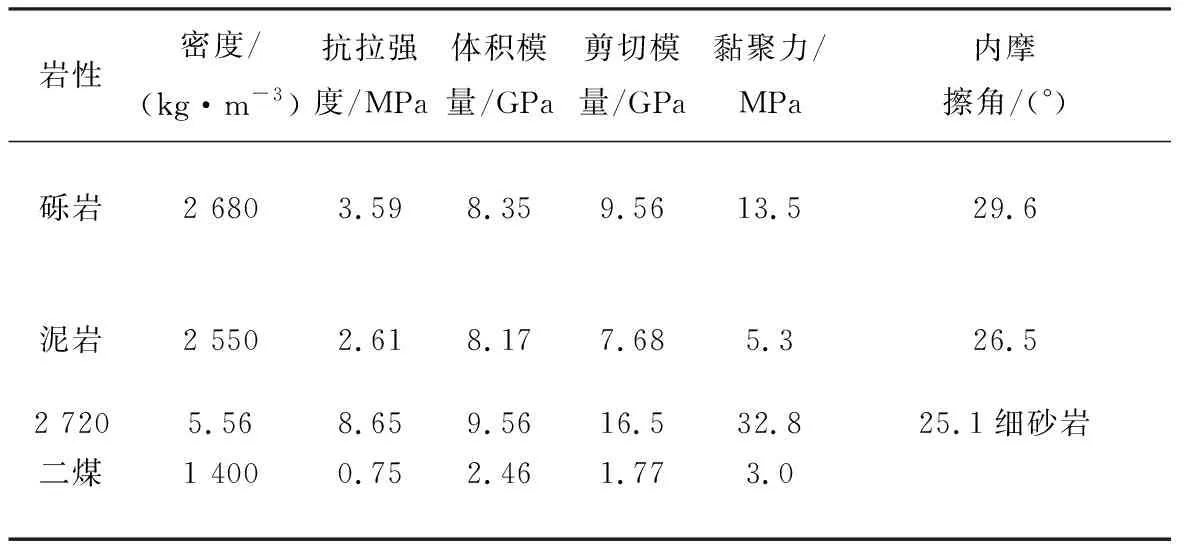
表1 各岩层物理力学参数Table 1 Physical and mechanical parameters of rock strata
由于义马煤田煤层顶板广泛分布着砾岩,该岩层厚度大、完整性好且抗变形能力强,煤层开采后不易破断垮落,从而导致大面积悬顶。这不仅造成采空区周边煤体出现应力集中,而且还使得采空区顶板容易积聚弹性能。已有研究表明,千秋矿煤层顶板砾岩厚度约为600 m,工作面开采后地表沉降量均较小,平均值分别为1.54 m和0.34[19]。因此,在进行数值模拟时,没有考虑工作面开挖后采空区垮落岩体力学特性对采动应力场的影响。
3.2 特厚煤层采动应力场特征
煤层的采出必然造成煤壁前方产生应力集中,即形成支承压力。相较于分层开采,特厚煤层采用放顶煤开采对采场围岩的扰动影响范围更大,超前支承压力峰值位置前移,且应力集中系数较高,可达2.0~3.5[20-21],如图7所示。

σ1、σ2、σ3—最大、中间、最小主应力;γ—覆岩容重;H—埋深图7 放顶煤开采工作面前方煤体应力分布Fig.7 Stress distribution of coal body in front of top-coal caving working face
大量理论研究和工程实践表明,采动应力集中是巷道大变形、冲击破坏、煤与瓦斯突出等灾害的主要诱发因素之一[22-23],并且塑性区形态和巷道所处的应力环境密切相关,因此为获得特厚煤层回采巷道塑性区演化规律,有必要掌握特厚煤层开采引起的采动应力场特征。
21141工作面开挖后,沿运输巷轴向提取工作面前方100 m范围内的最大主应力、最小主应力以及最大主应力与x轴的夹角,如图8所示。
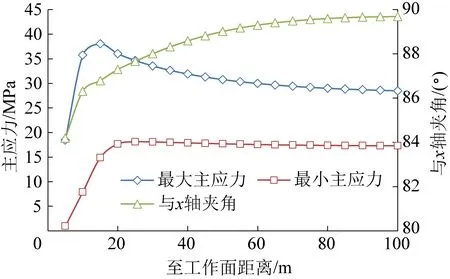
图8 工作面前方主应力、最大主应力与x轴夹角Fig.8 Principal stress and angle between maximum principal stress and x-axis
根据图8可以看出,工作面前方最大主应力和最小主应力的变化趋势差异较大。随着到工作面距离的增加,最大主应力呈现先急剧增大然后逐渐减小的趋势,并且最大主应力曲线斜率越来越小,最大主应力在距离工作面15 m处达到峰值,为38.03 MPa,而该位置的最小主应力为14.87 MPa,最大主应力是其2.56倍。由于煤层顶板厚度大且抗变形能力强,采空区顶板悬而不沉,造成工作面前方最大主应力明显大于原岩应力。同时,随着到工作面距离的增大,最大主应力方向与x轴夹角也逐渐增大,但是增速逐渐放缓,在距离工作面5 m处夹角为84.12°,距离工作面100 m处增大至89.69°。
3.3 特厚煤层回采巷道塑性区演化规律
为了分析特厚煤层回采巷道塑性区演化规律,根据千秋矿21141工作面运输巷工程地质条件,采用FLAC3D数值模拟软件建立拱形巷道塑性区数值计算模型,尺寸为80 m×80 m×1 m(图9),模型四周均为固定边界,竖直方向和水平方向分别施加边界载荷P1、P3,P1和P3可根据图8确定,模型中煤层倾角为12°。岩石物理力学参数见表1。
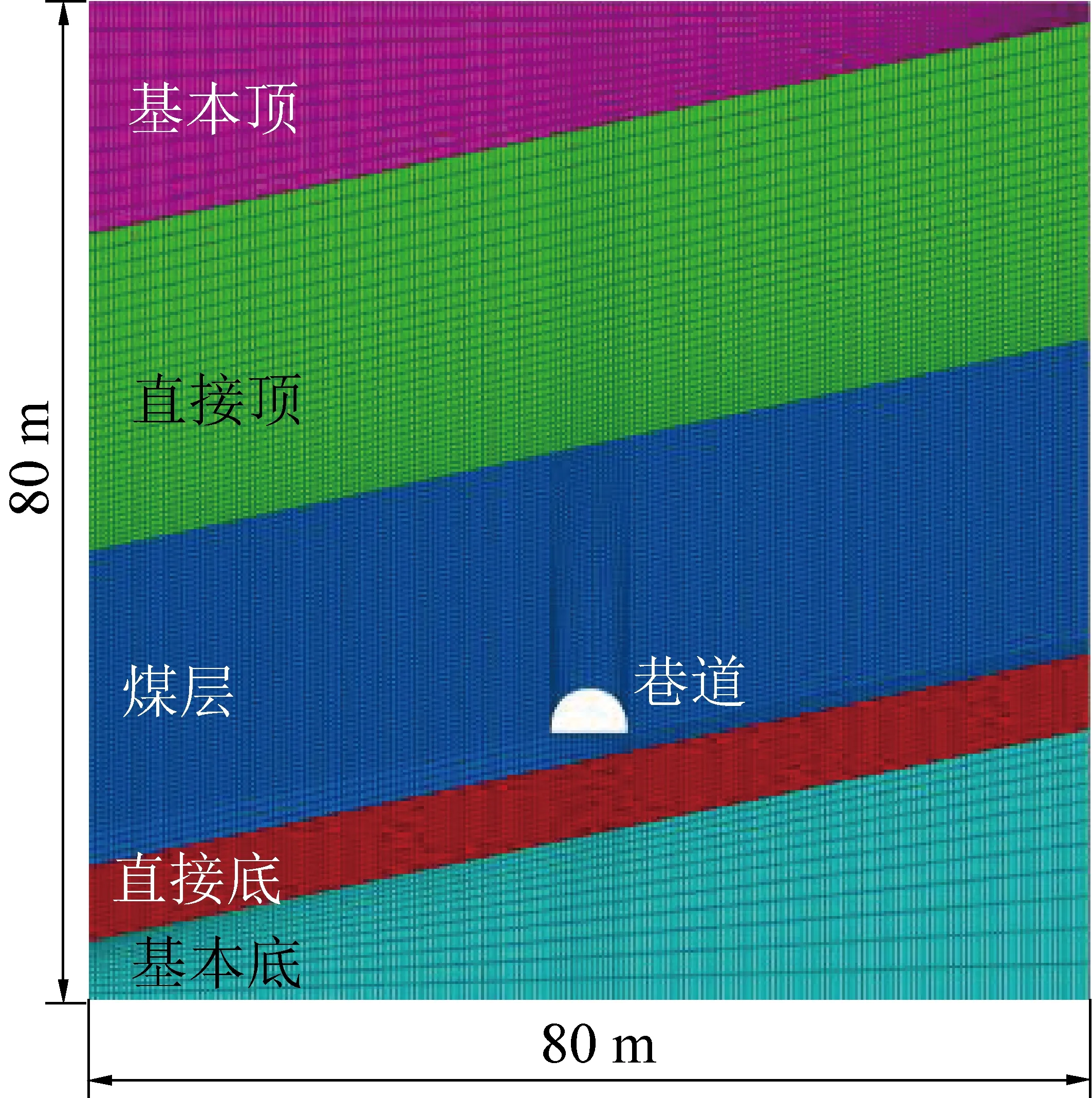
图9 拱形巷道数值计算模型Fig.9 Numerical calculation model of arch roadway
根据工作面前方主应力场分布规律,当21141工作面推进距离分别为400、450、465、485 m时,分别计算同一位置的塑性区特征,据此可以得出回采巷道围岩塑性区的演化规律(图10)。
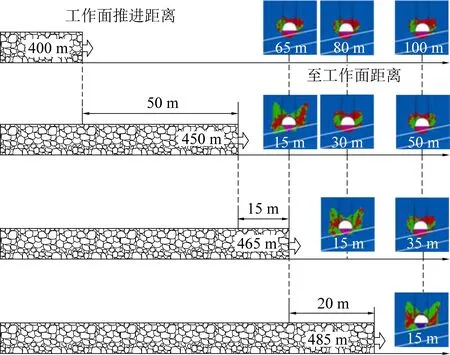
图10 回采巷道塑性区演化规律Fig.10 Evolution law of mining roadway plastic zone
由图10可得,随着工作面的推进,处于同一位置的巷道围岩塑性区形态特征不断发生变化,其两肩角持续向深部扩展,塑性区由不规则形态逐渐演化为蝶形。当工作面推进400 m时,距离工作面100 m处的巷道塑性区呈对称分布且形态不规则。随着工作面的继续推进,即工作面到该位置的距离不断减小,巷道两肩角的塑性区开始向围岩深部扩展,而顶板和底板塑性区深度变化却不明显,该位置的塑性区形态在工作面推进465 m演化为蝶形。当工作面推进485 m,即该位置到工作面的距离是15 m时,双向载荷比值P1/P3为2.56,塑性区蝶叶尺寸进一步增大,在肩角处向深部扩展,并且蝶叶方向发生了偏转。
工作面推进400 m时,距离工作面80 m处的巷道塑性区的形态和距离为100 m处一样,也呈对称分布且不规则。当工作面推进450 m,即该位置到工作面的距离为30 m时,巷道两肩角处的塑性区深度明显增大,而顶底板塑性区范围变化较小,塑性区形态呈蝶形;当工作面推进465 m,即该位置距离工作面15 m时,塑性区蝶叶尺寸进一步增大,并且发生了偏转。这表明工作面的回采使得回采巷道区域应力场(主应力的大小、方向)发生了改变,回采巷道塑性区的形态特征、最大尺寸及其方向等也随之变化。
4 结 论
1)塑性区形态特征与双向载荷比值有关。当围岩的力学性质相同时,巷道围岩塑性区的形态特征与应力条件密切相关。当双向载荷比值不大时,塑性区形态呈圆形或椭圆形,双向载荷比值达到某一值时,塑性区形态呈蝶形。
2)在采动应力影响下,回采巷道区域主应力场的大小和方向将发生改变。最大主应力沿回采巷道轴向呈先急剧增大后逐渐减小的趋势,并且在距离工作面15 m处达到峰值。随着到工作面距离的增大,最大主应力与x轴夹角逐渐增大并接近于竖直方向,最小主应力则在距离工作面约25 m处达到最大后缓慢减小。
3)工作面前方回采巷道塑性区的形态特征与区域主应力场的大小和方向密切相关。随着工作面的推进,同一位置到工作面的距离逐渐减小,特厚煤层回采巷道塑性区形态由不规则逐渐演化成蝶形,并且塑性区蝶叶位置会随着最大主应力方向的变化而发生偏转。研究成果可为特厚煤层开采方案设计、回采巷道支护参数确定等提供理论依据。
