芪黄通秘软胶囊吸湿动力学研究

乔子桐，付慧敏，张纯刚*，郭勇，程岚*（.辽宁中医药大学药学院，辽宁 大连 660；.神威药业集团有限公司，石家庄 05430）

芪黄通秘处方由黄芪、制何首乌、当归、肉苁蓉、黑芝麻、核桃仁等11 味中药材组成[1]，具有益气养血、润肠通便的功效[2]，因其含有大量挥发性成分而被制成软胶囊制剂，是《中国药典》2020年版一部新收录的成方制剂。

与其他中药固体制剂相比，软胶囊虽具有较高的生物利用度，但其在运输和储存过程中会发生崩解迟缓、渗漏和老化等现象，影响药品的质量与疗效。这些现象的发生均与软胶囊的含水量有关。一般说来，药品含水量的大小，除与制剂过程有关外，还与药物自身的吸湿性和其运输储存时的相对湿度（relative humidity，RH）有关。因此，研究软胶囊的吸湿过程对解决软胶囊的崩解迟缓、渗漏和老化等问题、提高软胶囊的质量与疗效具有重要的指导意义和应用价值。平衡含水率和药物吸收水分的质量变化率是研究药物吸湿特性和安全储存的重要参数，吸湿等温线和吸湿动力学曲线对于分析药物吸湿过程，指导药物的干燥、包装和储存也有一定的意义[3]。目前，已有研究者对中药饮片[4]、中药提取物[5]等的吸湿等温线和吸湿动力学曲线进行了考察，但没有对软胶囊制剂的吸湿过程进行较全面的研究。本试验通过研究芪黄通秘软胶囊在不同相对湿度环境下的吸湿情况，绘制吸湿等温线及吸湿动力学曲线，并用不同的数学模型对其进行拟合，获得最佳拟合方程，分析吸湿过程，以期为深入研究软胶囊的吸湿行为和探索高效的防潮策略提供理论指导。

1 材料

FA1004 万分之一电子天平（天津市天马衡基仪器有限公司）；WGL-230B 电热鼓风干燥箱（天津市泰斯特仪器有限公司）；玻璃干燥器（河北省蔚县玻璃器皿厂）；35 型培养皿（潍坊盛翔实验设备有限公司）；GM1361 分体式温湿度计（深圳市聚茂源科技有限公司）。MgCl2，K2CO3，NaBr，NaCl，KNO3均为分析纯（西陇科学股份有限公司）；纯净水（杭州娃哈哈集团有限公司）；芪黄通秘软胶囊（神威药业集团有限公司，规格：0.5 g/粒，批号：20112651）。

2 方法

2.1 芪黄通秘软胶囊吸湿等温线的测定

根据软胶囊实际生产中的储存和运输条件，在30℃条件下配制的6 种过饱和盐溶液（MgCl2，K2CO3，NaBr，NaCl，KNO3）和纯净水控制相对湿度。将盛有6 个过饱和盐溶液的干燥器于30℃下放置48 h，使其内部相对湿度保持恒定，利用分体式温湿度计测得不饱和盐的实际相对湿度与水分活度（Aw），见表1。精密称取芪黄通秘软胶囊，去包装后放入已恒重的培养皿中，记录数据。置于不同湿度条件下的干燥器中进行吸湿试验。300 h 后精密称定质量。计算此时芪黄通秘软胶囊的平衡含水率（EMC，见式1）。平行操作3 份。

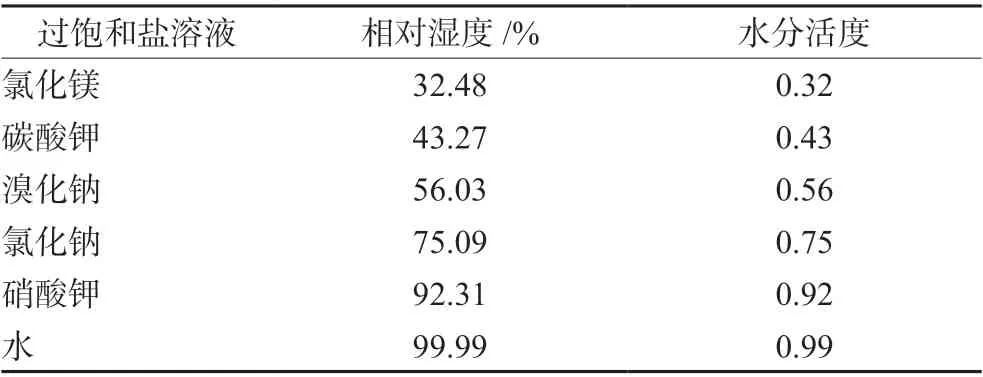
表1 30℃下不同溶液相对湿度表Tab 1 Relative hygrometer for different solutions at 30℃

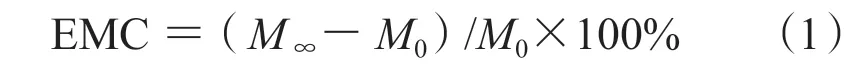
式中：M0和M∞分别代表初始样品质量（g）和平衡时样品的质量（g）。

2.2 芪黄通秘软胶囊吸湿等温线数学模型的建立

根据BET、GAB、Peleg、Smith、Halsey、Oswin 和Henderson 7 个数学模型[6]（见表2），采用OriginPro 2019b 软件对芪黄通秘软胶囊吸湿等温线进行非线性拟合。以决定系数（R2）和均根误差（RMSE）为指标，选择描述芪黄通秘软胶囊吸湿等温线的最佳拟合模型。

表2 吸湿等温线模型Tab 2 Models for hygroscopic isotherms

2.3 芪黄通秘软胶囊吸湿动力学曲线的测定

将盛有NaBr、NaCl、KNO33 种过饱和盐的干燥器于30℃放置48 h，使其内部相对湿度保持恒定。在3 个相对湿度条件下随机抽取3 份芪黄通秘软胶囊，去包装后分别于0、1、1.5、2、3、4、6、8、10、12、16、20、24、32、36、48 h 取出样品，并在30 s 内使用万分之一电子天平称定质量，48 h 后延长至每隔12 h 称定质量。水分吸收通过质量变化率来确定（式2）。

式中：M0和Mt分别代表初始样品质量（g）和t时刻样品的质量（g）。

当两次称定质量变化不超过±0.01%时，考虑样品达到了吸湿平衡。

2.4 芪黄通秘软胶囊吸湿动力学数学模型的选择

利用文献报道的6 种吸湿动力学模型[7]（见表3），描述芪黄通秘软胶囊在30 ℃相对湿度分别为56.03%、75.09%、92.31%下的吸湿动力学过程，采用OriginPro 2019b 软件对芪黄通秘软胶囊吸湿动力学曲线进行非线性拟合。以决定系数（R2）和均根误差（RMSE）为指标，确定芪黄通秘软胶囊吸湿动力学曲线的最优拟合模型。

表3 吸湿动力学模型Tab 3 Models for moisture adsorption kinetics

3 结果与分析

3.1 芪黄通秘软胶囊吸湿等温线

以水分活度为横坐标，EMC 为纵坐标，绘制芪黄通秘软胶囊的吸湿等温线，见图1。如图所示，样品的EMC 随水分活度的增加而增加。水分活度于0.4 左右EMC 平衡，后于0.6 处EMC 急剧增加。这一增长趋势可能与芪黄通秘软胶囊囊壳中的明胶有关。明胶中含有大量的蛋白质，对水有较大的吸附能力，出现毛细管凝结作用而产生样品平衡水分含量急剧增加的现象[8]。因此，考虑芪黄通秘软胶囊吸湿等温线模型可能是一个多层吸附模型。

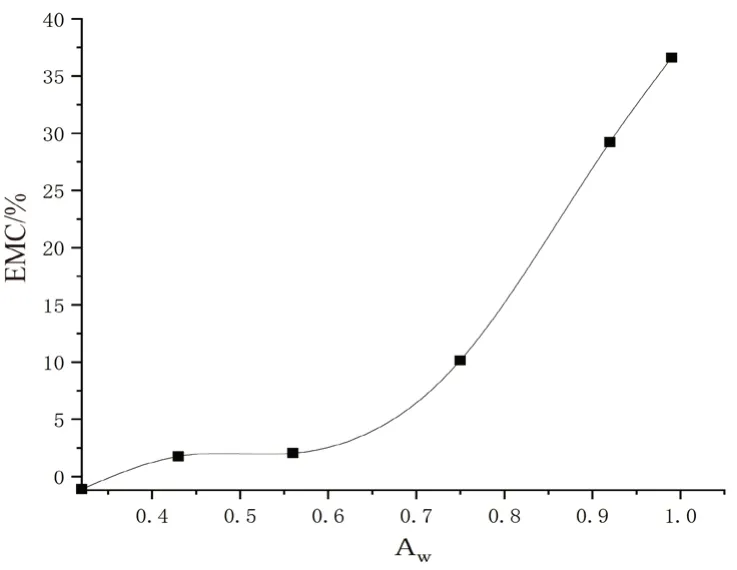
图1 芪黄通秘软胶囊吸湿等温线Fig 1 Hygroscopic isotherm of Qihuang Tongmi soft capsules

3.2 芪黄通秘软胶囊吸湿等温线数学模型的拟合与分析

如表4 所示，在GAB 模型中由于0 ＜k＜1，c＞2，可以判定芪黄通秘软胶囊吸湿等温线属于Ⅱ型等温线[9]。且其吸湿等温线图（见图1）也与国际理论和应用化学联合会（IUPAC）规定的Ⅱ型等温线图形相似。证明芪黄通秘软胶囊具有非晶态和多孔结构，同时具有单层吸附和多层吸附的位点[10]，其吸附模型为多层吸附模型。符合此类吸附模型的样品即使当其自身达到平衡后，环境相对湿度继续增加，其吸湿量仍会持续增加，吸附层数将趋于无穷大[11]。因此，根据软胶囊实际生产中的储存和运输条件，芪黄通秘软胶囊应控制环境温度30℃，相对湿度不超过60%。

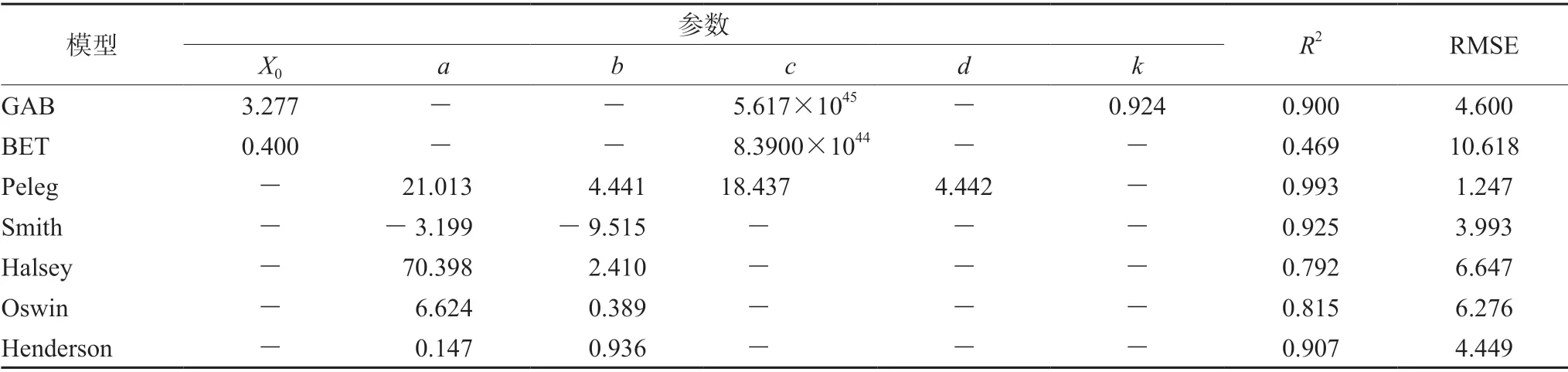
表4 吸湿等温线模型参数Tab 4 Model parameters of hygroscpic isotherms

近年来，吸附等温线也常被应用于材料表面微观结构的分析。表2 的7 个模型中，只有GAB模型和BET模型可用于估计粉末等固体物质的单分子层容量和比表面积[12]。但在大多数研究工作中，Peleg模型被认为是一种与GAB 模型相似甚至更好的用于描述水蒸气吸附的模型[13]。本文也证实Peleg 模型与其他6 种模型相比，能够更好地描述芪黄通秘软胶囊在30℃，水分活度0.32～0.99条件下的吸附行为（R2更接近于1，RMSE更接近于0）。其表达式为：EMC＝21.013Aw4.441＋18.437Aw4.442。

3.3 芪黄通秘软胶囊吸湿动力学曲线

以时间t为横坐标，质量变化率平均值为纵坐标绘制出吸湿动力学曲线，见图2。结果表明，随着湿度增高，芪黄通秘软胶囊的达平时间逐渐增长，质量变化率逐渐增大。其在达平前均会出现质量变化率轻微下降的现象（但两次称定质量不超过±0.01%）。这可能与水分子之间的氢键和吸湿物质中的极性位点的结合程度有关。低温下，水分子与吸湿物质的极性位点紧密结合[14]。但水分子的吸附是一种放热反应，当温度升高使这些位点的水结合能力降低[15]，水分子将从吸湿物质毛细管系统表面分解，分子的动能增加，使得水分子与吸湿物质毛细管系统表面极性位点之间的相互吸引变得困难。因此，水分子之间的氢键和吸湿物质中的极性位点的结合程度降低，造成样品水分含量的减少而至其平衡后的质量变化率有轻微下降。

图2 芪黄通秘软胶囊动力学曲线Fig 2 Moisture dynamics curves of Qihuang Tongmi soft capsule

3.4 芪黄通秘软胶囊吸湿动力学曲线模型的拟合

芪黄通秘软胶囊对水的吸附速率随着处理时间的增加逐渐降低。吸湿动力学曲线模型的拟合结果表明，在相对湿度分别为56.03%、75.09%、92.31%下双指数模型拟合效果均为最佳，模型参数如表5 所示。这可能是由于相对于其他几种数学吸附模型来说，双指数模型考虑了影响水分子扩散的复杂因素，尤其反映了水分子真实运动的受限程度，这也表明芪黄通秘软胶囊吸湿行为可能同时存在两种机制[16]，即扩散机制和双位吸附机制，相关数据有待进一步说明。

表5 吸湿动力学模型参数Tab 5 Model parameters of moisture dynamics curves

因此，为了防止水分子的扩散，降低芪黄通秘软胶囊吸湿速率，可在其运输和储存过程中加装除湿机以降低环境湿度，采用瓶装、纯铝材料包装也可有效地减少水分的渗入，在包装中适当使用干燥剂也可降低水分对药物的影响。

4 结论

芪黄通秘软胶囊的等温吸附线属于Ⅱ型等温线，样品的EMC 随水分活度的增加而增加。经比较发现Peleg 模型能更好地解释芪黄通秘软胶囊在30℃下的吸附行为，其表达式为：EMC ＝21.013Aw4.441＋18.437Aw4.442。研究芪黄通秘软胶囊水分吸湿等温线可以确定其安全储存的含水率。通过芪黄通秘软胶囊的吸湿动力学曲线可知，随着湿度增高，芪黄通秘软胶囊的达平时间逐渐增长，质量变化率逐渐增大。与其他模型相比，双指数模型能更好地解释芪黄通秘软胶囊在30℃下的吸附动力学行为。相对湿度为56.03%时，其数学表达式为y＝2.166－1.135e－0.075t－1.128e－0.075t；相对湿度为75.09%时，其数学表达式为y＝10.668－4.907e－0.09t－5.882e－0.021t；相对湿度为92.31%时，其数学表达式为y＝30.985－8.748e－0.0134t－22.342e－0.009t。