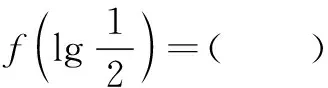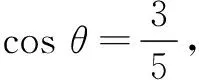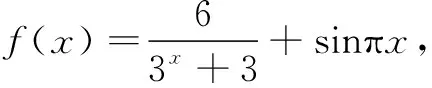高一数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1.已知集合A={x|x2-2x-8<0},B={x|x>0},则A∩B=( )

(A) {x|x>2}

(B) {x|0

(C) {x|0

(D) {x|2

3.已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )

(A)x2cosx(B)x+x3

(C) |x|sinx(D)x2+cosx

(A) 1 (B) 2 (C) 3 (D) 4

(A)a

(C)a

(A) 2 019 (B) 2 021

(C) 2 020 (D) 2 022

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,有选错的得0分)

9.下列各组函数中,表示同一函数的是( )

(A)f(t)=t2,g(x)=x2

10.已知定义在R上的偶函数f(x)在(-∞,0)单调递增,则下列结论正确的是( )

(A)f(x)在(0,+∞)上单调递减

(B)f(x)最多有两个零点

(C)f(log0.53)>f(log25)

11.下列说法正确的是( )

(A) “ac2>bc2”是“a>b”的充分不必要条件

(B) “xy>0”是“x+y>0”的必要不充分条件

(C) “对任意一个无理数x,x2也是无理数”是真命题

(D) 命题“∃x∈R,x2+1=0”的否定是“∀x∈R,x2+1≠0”

12.已知a>0,b>0,a+b=2,下列说法中正确的是( )

(C) lga+lgb≤0 (D)a2+b2≤2

三、填空题(本大题共4小题,每小题5分,计20分)

14.函数f(x)=ax+logax在[1,2]的最大值和最小值之差为|a2-a|+1,则a=______.

15.已知函数f(x)满足f(x)=f(2-x),当x≥1时,f(x)=2-x2.若不等式f(2x-a)>-2的解集是集合{x|1

四、解答题(本大题共6小题,计70分.解答时应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知集合A={x|a

(1)当a=2时,求A∪(RB);

(2)若A⊆RB,求a的取值范围.

18.(本小题满分12分)已知函数f(x)=4x-2·2x+1+a,其中x∈[0,3].

(1)若f(x)的最小值为1,求a的值;

(2)若存在x∈[0,3],使f(x)≥33成立,求a的取值范围.

(1)求该噪声声波曲线的解析式f(x)以及降噪芯片生成的降噪声波曲线的解析式g(x);

20.(本小题满分12分) 已知二次函数f(x)满足f(1)=-9,且不等式f(x)+3x<0的解集为(-1,4).

(1)求f(x)的解析式;

(2)若函数f(x)在x∈[0,t]时的值域为[-13,-4],求t的取值范围.

21.(本小题满分12分)已知函数f(x)=log2(x2-ax+a+3).

(1)若f(x)定义域为R,求a的取值范围;

(2)若f(x)≥1对x∈[2,3]恒成立,求a的取值范围.

(1)求证:函数f(x)为奇函数;

(2)若当x∈(0,1)时,f(x)<0,求证:f(x)在(-1,1)单调递减;

参考答案

一、单项选择题

1. C;2. D;3. C;4. A;5. C;

6. A;7. B;8. B.

二、多项选择题

9. ABD;10. ACD;11. AD;12. BC.

三、填空题

15.2≤a≤4;16.0

四、解答题

17.(1)由题意得A={x|2

(2)A⊆RB.

当a≤0时,A=∅,符合题意.

18.(1)因为x∈[0,3],f(x)=(2x)2-4·2x+a=(2x-2)2+a-4,所以当2x=2,即x=1时,函数f(x)取得最小值,即f(x)min=f(1)=a-4=1,解得a=5.

(2)令t=2x∈[1,8],则f(x)=t2-4t+a,由f(x)≥33,可得a≥-t2+4t+33.

令g(t)=-t2+4t+33,则g(t)在[1,2)单调增,在(2,8]单调减.又g(1)=36,g(8)=1,所以g(t)min=g(8)=1.

综上,可得a≥1.

20.(1)因为f(x)为二次函数,所以f(x)+3x<0为一元二次不等式,可设f(x)+3x=a(x+1)(x-4),得f(x)=ax2-3(a+1)x-4a.

由f(1)=-9,得-6a-3=-9,解得a=1.所以f(x)=x2-6x-4.

(2)因为f(x)=x2-6x-4=(x-3)2-13,所以当x=3时,f(x)取最小值-13.

又由f(x)=-4,得x=0或x=6.结合f(x)的对称性,可知3∈[0,t],且t≤6,所以3≤t≤6.

所以t的取值范围为[3,6].

21.(1)由题意得x2-ax+a+3>0恒成立,所以Δ=a2-4(a+3)<0,解得-2