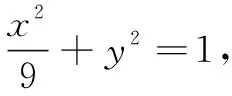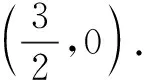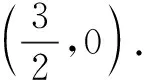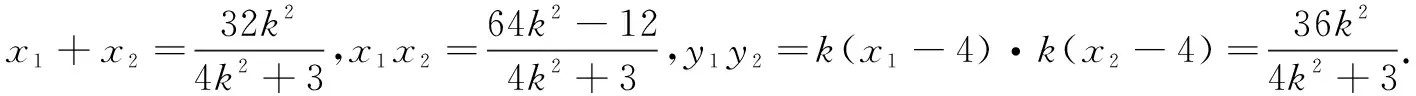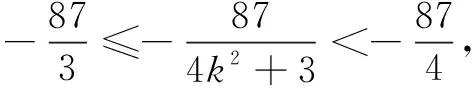巧用梅涅劳斯定理求解直线过定点问题

陈沙沙 胡廷佳 屈大海

(贵州省遵义市第五十四中学,563102)

圆锥曲线问题是高中数学的重要内容,解题时容易陷入计算复杂的瓶颈.如何避免用解析几何常规方法求解的复杂计算? 经研究,笔者惊奇地发现圆锥曲线过定点的问题可用梅涅劳斯定理来解决,并且可以完美避开复杂的计算.现整理成文,供大家分享.

一、背景知识

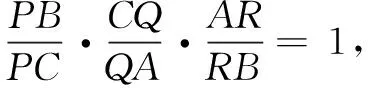
证明如图2,设P,Q,R三点中有P,R两点在∆ABC的边上,另一点Q在AC边的延长线上.

评注梅涅劳斯定理和及其逆定理有非常广泛的应用,它们是证明平面上三点共线的有力工具.

二、应用举例

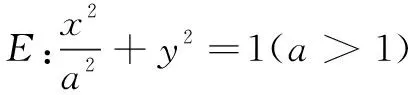
(1)求E的方程;

(2)证明:直线CD过定点.

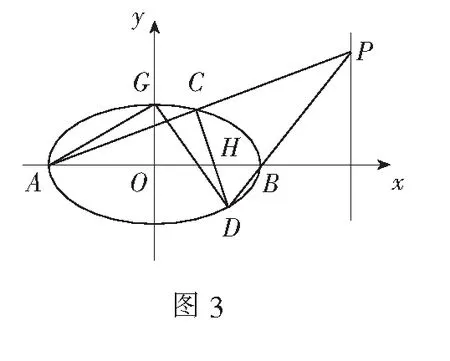
当t≠0时,设直线CD的方程为x=my+n(-3

解法2设点P(6,t),C(x1,y1),D(x2,y2),直线CD与x轴交于点H(x0,0),显然-3

(1)求椭圆C的方程;

(2)设椭圆C的左、右顶点分别为A,B,点P是直线x=1上的动点,直线PA与椭圆交于另一个点M,直线PB与椭圆交于另一个点N,求证:直线MN经过一定点.

因为AB=4,GA=GB+AB,所以3GB=GB+4,得GB=2.故直线MN过定点G(4,0).

(1)求椭圆C的方程;

(3)若点B关于x轴的对称点是E,证明:直线AE与x轴相交于定点.

(3)如图5,设直线BE,AE与x轴的交点分别为R,Q.由B,E关于x轴对称,得RE=RB.设点E(x2,-y2),Q(x,0),R(x2,0).

所以直线AE与x轴相交于定点Q(1,0).