发展数学思维 提升解题能力——以“多元变量最值与范围问题”教学为例

赵 亮 李令军

(江苏省扬州大学附属中学，225002)

一、引言

《普通高中数学课程标准(2017)版》指出，高中数学课程应注意提高学生的数学思维能力,这是数学教育的基本目标之一[1]. 在最新高考评价体系中,作为学科素养指导体系,强调了“知识整合”,根据应对问题情境的需要合理地组织、调动各方面相关知识和能力;强调“创新思维”,组织相关知识与能力，注重发散性,提出新视角、新方法[2]. 众所周知,解题是学生提高数学思维能力的重要途径之一.在数学解题教学中,我们首先要帮助学生知道如何解题,做到心中有“路”;其次，还要注重提高学生发散性思维和创新性思维,引导学生进行有效的反思总结、内化方法.本文以多元变量最值与范围问题的解题教学为例,探讨如何培养学生的数学思维和解决问题能力,以期抛砖引玉.

二、发展思维，提升能力

1.真题教学,启迪思维

例1(2020年全国高考题)在∆ABC中,已知sin2A-sin2B-sin2C=sinBsinC.

(1)求A;

(2)若BC=3,求∆ABC周长的最大值.

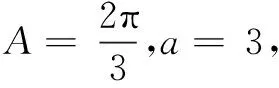
思考1边化角,用消元法化二元为一元,利用函数研究最值.

思考2由b2+c2+bc=9联想x2+y2=R2模型,用三角换元化二元为一元,利用函数研究最值.

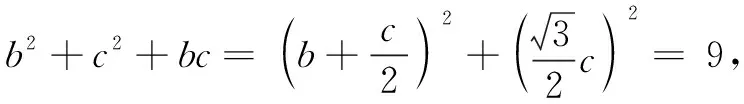
思考3由b2+c2+bc=9联想基本不等式模型,利用和、积形式转化构建不等关系求解.

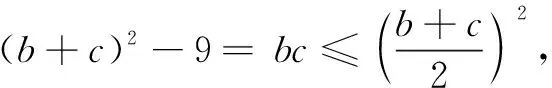
思考4记b+c=t,换元转化为方程组有解问题.

思考5数形结合,记b+c=t,转化为轨迹有交点问题.

解法5令b+c=t,则问题可看作动点P(b,c)在曲线b2+c2+bc=9 上移动,且直线b+c=t与曲线b2+c2+bc=9 有交点.如图1,当直线与曲线相切时t取得最值.

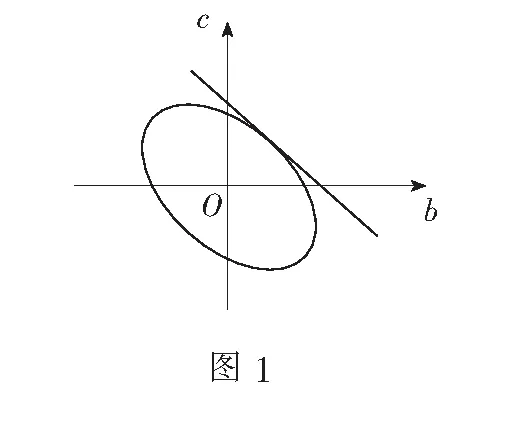
综合解法1-4我们可以看到,转换问题视角,即分别从函数、方程、不等式等方面将最值问题实现有效转化,再利用各自的思路即可实现问题的求解;而解法5则是通过数形结合将问题转化为轨迹交点问题,使目标对象在相切时取最值.解题的总体策略如图2所示.

在不同的解题路线下,函数、方程、不等式、解析几何知识的融会贯通是问题获解的认知基础.作为思路寻求及问题得解,我们再看浙江省的一道高考题.

2.尝试应用,内化方法

例2(2014年浙江高考题)若a+b+c=0,a2+b2+c2=1,则a的最大值是______.

应用1函数视角

应用2不等式视角

应用3方程视角

应用4解析几何视角

应用5转化思想

三、优选方法,形成经验

多元变量的最值与范围问题一直是高考命题的热点,解决这类问题一般需要较强的分析能力、较多的思想方法、较高的变形技巧.但是通过以上的解题研究,我们可以让学生皆能做到心中有“路”,并且 “路”上有章可循.下面数例为上述例题的变式问题,通过进一步寻找解决问题的途径,归纳共性,即可优选方法、形成经验.

变式2(2018年江苏高考题)已知x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.(参考答案:4)

G·波利亚有一句脍炙人口的名言:“掌握数学就是意味着善于解题”,顾名思义,学好数学就需要解题,并在解题的过程中学到知识、积累经验、凝练方法,逐步的形成一套规范的、系统的、科学的解题活动.当然,这一过程需要时间和经验(量)的保证,更离不开研究方法和思维方式(质)的飞跃.要实现如此飞跃,需要在教学中注意以下几点:

(1)培养发散思维,多渠道寻找问题求解之路,不断变换问题,开拓新路.教学中要引导学生多角度去思考问题,以寻求多种想法、观点或答案,如此拓展为多角度思维空间,实施过程中要注意流畅性、变通性.从问题到函数模型、方程模型、不等式模型,流畅性是关键,而问题的转换则是变通性.

(2)注重深度挖掘,用相关联知识表征反映问题的本质.高中数学教学追求发展学生的核心素养,这就必须引导学生进行深度学习. 教学中注意引导学生通过多种表征方式的探究,尽可能丰富问题的关联知识,在强化关联的同时注意学习的沉浸性.