赏析运用“函数积k性质”命制的导数试题

陈凌燕

(福建省厦门市海沧中学，361022)

一、 引言

函数是数学的一条重要主线,其概念和性质贯穿整个函数内容的学习,更是高考考查的重点内容.在高考试题中,一般将函数的单调性、零点等性质与导数交汇,综合考查学生逻辑推理、数学抽象等核心素养,体现试题的基础性、综合性、创新性.笔者在一些导数试题中抽象出函数的一类性质,类比函数的奇偶性定义,提出函数的积k性质.

二、函数的积k对称性

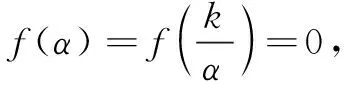
若f(x)是积k反称函数,同理可证有类似的性质.

由积k对称函数、积k反称函数的定义,不难证明如下性质(具体过程略).

性质3若f(x)是积k反称函数,则|f(x)|,(f(x))2是积k对称函数.

由性质4,通过适当的运算组合可以构造结构优美的函数.

三、函数的积k性质的应用

积k对称或反称函数虽并不少见,但由于不是教材中所提及的类似函数的奇偶性、单调性、周期性等函数的基本性质,学生做题时,并不容易反应到需要研究函数的这类性质.因此,以此类函数为载体命题,具有考查能力要求高、难度大、区分度强的特点,素养导向十分明显,很有研究价值.

1.利用函数的积k性质判断零点个数

(1)讨论f(x)的单调性,并证明f(x)有且仅有2个零点;

(2)略.

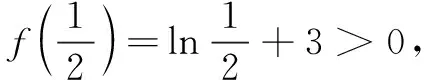
综上,f(x)有且仅有两个零点.

变式(2019年全国高考题)已知函数f(x)=(x-1)lnx-x-1证明:

(1)f(x)存在唯一的极值点;

(2)f(x)=0有且仅有2个实根,且它们互为倒数.

例2已知函数f(x)=(x2+1)lnx-m(x2-1),则下列结论正确的是( )

(A)当m=0时,曲线y=f(x)在点(1,f(1))处的切线方程为y=2x

(B)当m≤1时,f(x)在定义域内单调增

(C)当m>1时,f(x)既存在极大值又存在极小值

(D)当m>1时,f(x)恰有3个零点x1,x2,x3,且x1x2x3=1

简析本题是多选题,考查利用导数研究函数的切线、单调性、极值、零点等基本性质.对选项D,常规解法较为繁琐,而利用反称函数及其性质可快捷求解.

2.利用积k函数的零点性质研究参数的取值范围

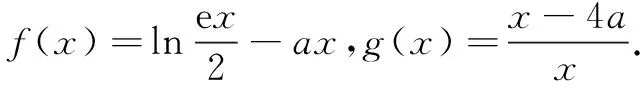
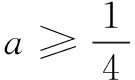
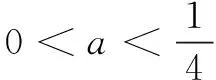
3.研究积k函数的零点性质

(1)讨论f(x)的单调性;

当a>2时,x2+2x-2ax+1=0有2个不等实根α,β(α<β),且αβ=1,易知f(x)在(0,α)单调增,在(α,β)单调减,在(β,+∞)单调增.

四、结束语

研究函数的积k对称性,对于解决一些特殊的导数压轴试题具有很好的化繁为简作用,同时也给教师命制导数类试题提供了很好的构造函数、设置创新性问题的一条途径.

归纳抽象一些常见函数中的性质,对于教师提升自身素养,以及指导学生进行解题反思,提升学生探究创新能力等都具有相当重要的意义.