颗粒饲料破损离散元仿真参数标定
2022-08-08牛智有孔宪锐沈柏胜李洪成
牛智有 孔宪锐 沈柏胜 李洪成 耿 婕 刘 静
(1.华中农业大学工学院, 武汉 430070; 2.农业农村部长江中下游农业装备重点实验室, 武汉 430070)
0 引言
随着我国水产养殖规模不断增加,投饲需求相应增加,其中,气力输送因其结构简单、输送距离可控等优点而被广泛应用,基于气送式的投饲装置也应运而生[1-3]。目前,对气送式投饲装置的研究主要围绕定时定量精准投饲、集成化控制、水体信息的感知和远程投饲等功能开展[3-6],有关饲料在输送过程中破损现象的研究还相对较少。然而,在气力输送过程中饲料破损问题十分显著,大量的破损颗粒被投到养殖水体中,造成饲料浪费严重、水体环境恶化、养殖效率低等诸多问题[7]。因此,为了降低饲料在气送过程中破损率,进行饲料破损机理的研究十分必要。
早期关于饲料破损问题的研究大都基于传统试验方法[8-9]。近年来,离散元技术和CFD-DEM(计算流体力学-离散单元法)耦合技术得到广泛应用[10-13],为分析颗粒饲料受力、碰撞和破损等问题,探明饲料破损机理提供一种新的方法。由于颗粒饲料种类及其几何结构的多样化,为了确保仿真模型所用参数的准确性,需要对模拟所用参数进行标定。
学者们对农业物料的参数标定进行了大量研究[14-19]。目前,物料的参数主要存在两种标定方法,一种是整体标定方法,另一种是直接测量方法[20]。整体标定法是通过现场或实验室测量材料整体特性,按照实际条件进行数值模拟,通过不断调整DEM参数来获得相同的整体响应;直接测量法则是通过直接测定粒子或接触水平的属性值作为标定参数[21]。文献[22]基于试验测量,完成了颗粒饲料的密度、弹性模量、接触参数等的测定,但未进行饲料间碰撞恢复系数的测定;文献[23]确定了两种饲料颗粒的数值模拟模型及一些仿真参数,但未对获取的参数进行标定;文献[24]基于注入截面法,设计了一种新型休止角测量装置,且通过休止角试验与仿真测量结果对比,完成了滑动摩擦因数、碰撞恢复系数、滚动摩擦因数的标定,但未对饲料的破碎物理参数进行标定;文献[25]基于仿真与试验结合,完成了饲料油菜茎秆基本接触参数和破碎参数的标定,但未对破碎模型的接触参数进行验证。
为了探究饲料的破损机理,形成一套合理、完善的颗粒饲料破损评价方案,本文针对混养成鱼颗粒饲料进行试验及仿真参数标定。基于EDEM软件,首先采用Hertz-Mindlin模型建立颗粒饲料多球模型,通过休止角试验和碰撞恢复系数标定试验,结合试验优化设计手段,进行颗粒饲料基本接触参数的标定;其次采用Hertz-Mindlin粘结模型建立颗粒饲料粘结模型,通过单轴压缩物理试验和仿真试验,结合试验优化设计手段,进行粘结参数的标定。最后,验证粘结模型接触参数的准确性。
1 材料与方法
1.1 试验样品
所用样品取自饲料生产企业混养成鱼颗粒饲料。分别采用排沙法和干燥法测定5组平行样品的密度和含水率,取平均值,测得颗粒饲料密度为1 086.15 kg/m3、含水率为10.78%;随机选取100个样品,采用数显式游标卡尺(精度0.01 mm)测量颗粒直径和长度,经统计计算,获得颗粒平均直径为2.67 mm、平均长度为8.89 mm。
1.2 参数测定方法
1.2.1力学特性参数
为获取颗粒饲料弹性模量和泊松比,利用TMS-Pro型质构仪(FTC公司,美国)对颗粒饲料进行单轴压缩试验和破碎试验,试验过程中压头速度均设置为10 mm/min。在进行试验前,对试验样品进行预制,采用360目细砂纸对其进行打磨,使两端磨平,长度维持在样品测量平均值8.89 mm左右。通过单轴压缩试验前后颗粒饲料高度和直径的变化,计算得到其弹性模量和泊松比平均值分别为245.94 MPa和0.387;通过单颗粒压缩破碎试验,获得平均破碎力为36.22 N。
1.2.2休止角测定
本文采用漏斗法测量颗粒饲料休止角(Angle of repose, AoR)[26]。由于气送式饲喂多采用塑料软管作为输送管道,所以采用软塑料(软PVC)紧贴漏斗内壁,以考察颗粒与软PVC间的接触特性。选取颗粒饲料平均质量为124.04 g,获取5次休止角试验的颗粒堆积图像。对原始图像进行灰度化、二值化、轮廓提取、直线拟合及角度识别等处理,获得颗粒饲料休止角,如图1所示。通过统计计算,试验样品休止角的平均值为28.18°。此外,对5组试验的落料时间进行记录,落料时间平均值为1.26 s。

图1 休止角图像处理Fig.1 Image processing of AoR
1.2.3碰撞恢复系数标定试验
为了充分考虑颗粒初始下落状态的随机性以及颗粒在运动过程中的自旋的影响,本研究搭建一套碰撞恢复系数测量装置[27],分别进行颗粒-颗粒间和颗粒-软PVC间碰撞恢复系数的标定,如图2所示。随机选取200颗颗粒饲料进行碰撞恢复系数标定试验。操作过程如下,将接收盘划分为6个尺寸完全相同的栅格,在释放管上方进行自由落料,每次落料量为1颗,直至200颗饲料落料完全,统计每个栅格中存在的颗粒饲料的数量,计算平均栅格数I,通过平均栅格数间接标定碰撞恢复系数,公式为

图2 碰撞恢复系数标定试验装置Fig.2 Coefficient of restitution calibration test setup
(1)
式中Ntotal——总颗粒数量
n——总栅格数量
Ni——第i个栅格中的颗粒数量
通过统计,各个栅格饲料颗粒数如表1所示。
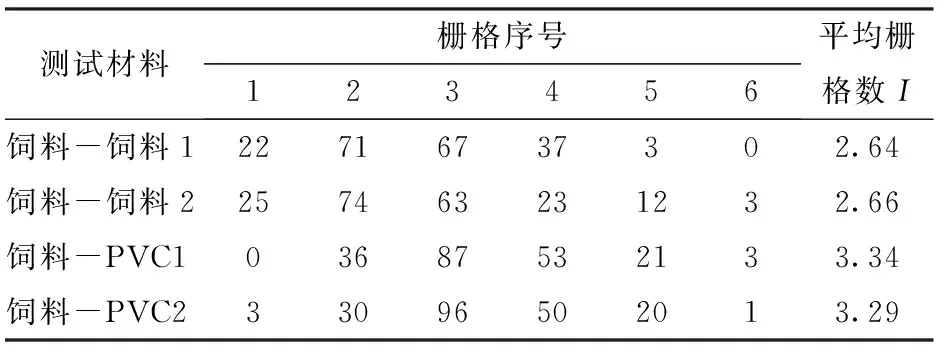
表1 各栅格颗粒数及平均栅格数Tab.1 Particle numbers in each bin and average bin number
1.3 仿真模型建立
1.3.1颗粒饲料休止角仿真模型
本研究采取多球模型建立颗粒饲料离散元模型[23-24,28],综合考虑形状拟合和颗粒数量两个因
素,采用15个直径为2.67 mm的球体相互拼接,形成如图3所示的颗粒模型。基于EDEM软件中通用材料(Generic EDEM material model, GEMM)数据库以及预仿真试验,确定了颗粒饲料和软PVC仿真参数的取值范围,如表2所示。

图3 颗粒饲料多球模型Fig.3 Multisphere model of pellet feed

表2 颗粒饲料休止角仿真模型参数Tab.2 Parameters of AoR simulation model for pellet feed
为了保证颗粒粒度的随机分布,在EDEM软件中选择颗粒尺寸分布为正态分布,其标准差为0.05。为了限制最大最小粒度,Cap低值设置为0.96,高值设置为1.05。在EDEM中建立圆锥体作为颗粒工厂,采用静态生成方法,生成颗粒质量为124.04 g,待颗粒完全静止后,给定抽板运动设置,颗粒开始下落。仿真模型如图4所示。

图4 颗粒饲料休止角仿真模型Fig.4 Simulation model of AoR for pellet feed
1.3.2碰撞恢复系数测量装置仿真模型
将实际模型中的释放管简化为圆形颗粒工厂,冲击板分别由饲料和软PVC组成,按照实际厚度绘制。栅格采用硬PVC材料参数进行设置,石英砂按照其材料参数进行设置。所得仿真模型如图5所示。
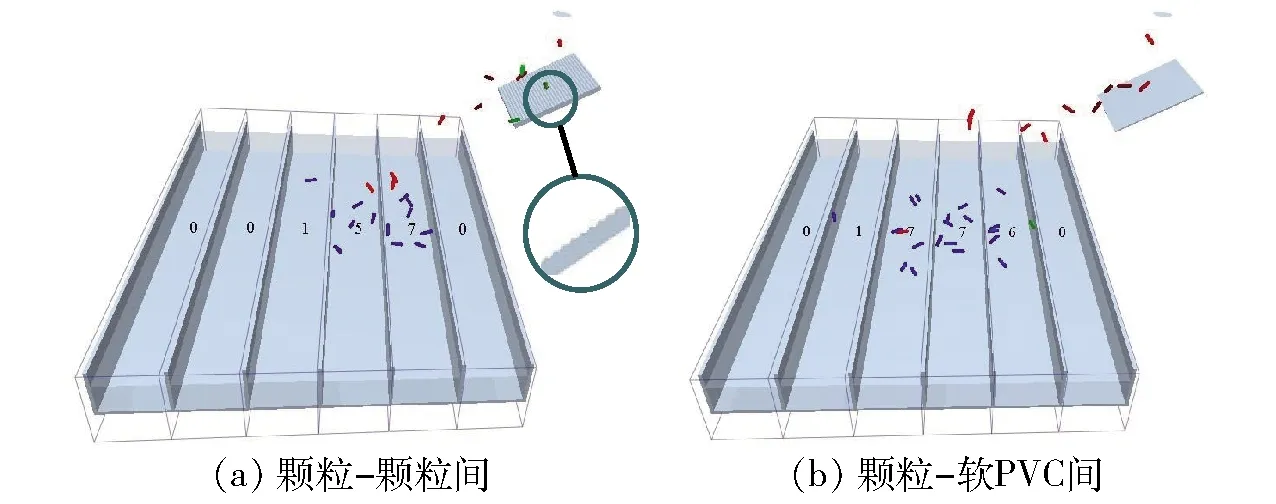
图5 碰撞恢复系数标定试验仿真模型Fig.5 Simulation models for coefficient of restitution calibration test
1.3.3颗粒饲料破损仿真模型
在EDEM中,基于Hertz-Mindlin粘结接触理论,用微粒粘结生成如图6所示的粘结模型,替代原有的多球模型。具体流程如下,建立半径为0.20 mm的微粒模型和直径为2.67 mm、长度为8.89 mm、关于原点中心对称的圆柱颗粒模型,使用小颗粒对圆柱体进行填充;然后,建立压头和支撑板模型,设定压头运动速度为10 mm/min,颗粒最大压缩距离为3 mm。
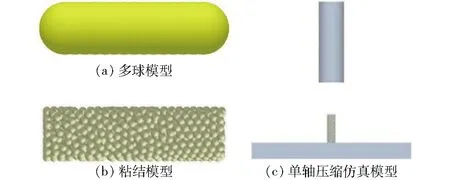
图6 颗粒饲料单轴压缩破坏仿真模型Fig.6 Simulation model of feed breakage under uniaxial compression
微粒基本接触参数采用已有参数,通过径向压缩和轴向压缩预仿真试验获得的粘结参数取值范围如表3所示。为了保证粘结模型的质量等于实际饲料质量,采用密度放大法[30],将微粒的密度由1 086.15 kg/m3放大至2 045.74 kg/m3,其余参数保持不变,以保证粘结模型的质量与实际饲料质量相等。

表3 颗粒饲料粘结参数Tab.3 Bonding parameters of pellet feed
1.4 参数标定试验设计
1.4.1休止角试验参数标定
首先,通过Design-Expert软件进行二水平因子试验设计筛选出对休止角影响显著的参数,选择表2中参数A~F的上下限作为高低水平展开仿真试验,试验共16次;其次,对影响显著的参数进行爬坡试验设计,开展一系列休止角仿真试验,以确定最优值的取值范围。其中,影响不显著的参数取中间水平,显著因素按照给定步长逐步增加;最后,基于上述试验结果,根据BBD(Box-Behnken design)设计原理,取显著因素的高、中、低3个水平开展休止角仿真试验。非显著性参数取值同最陡爬坡试验[25]。
1.4.2碰撞恢复系数标定
使用Design-Expert进行单因素试验设计,在表2给定的碰撞恢复系数的取值范围中选择一系列参数水平进行仿真试验。以实测平均栅格数为目标,利用Numerical模块进行参数预测,并将预测参数进行仿真验证。
1.4.3滚动摩擦因数标定
使用Design-Expert进行单因素试验设计,在表2给定的颗粒饲料-软PVC滚动摩擦因数的取值范围中选择一系列参数水平进行仿真试验。以实测落料时间为目标,利用Numerical模块进行参数预测,并将预测参数进行仿真验证。
1.4.4粘结参数标定
首先进行预仿真试验,将x1、x2设定为1×109N/m3,其余两参数不断变化,得出临界应力影响不显著,如表4所示,故将其设定为中间值455 MPa和305 MPa。

表4 单轴压缩破碎预仿真试验Tab.4 Pre-simulation test of uniaxial compression breakage
为保证标定参数的可靠性,避免参数值超过取值范围,根据CCD(Central composite design)原理进行响应曲面试验设计,以标定的接触参数和待标定的粘结参数建立模型,开展颗粒饲料单轴压缩破碎仿真试验,粘结参数编码如表5所示。
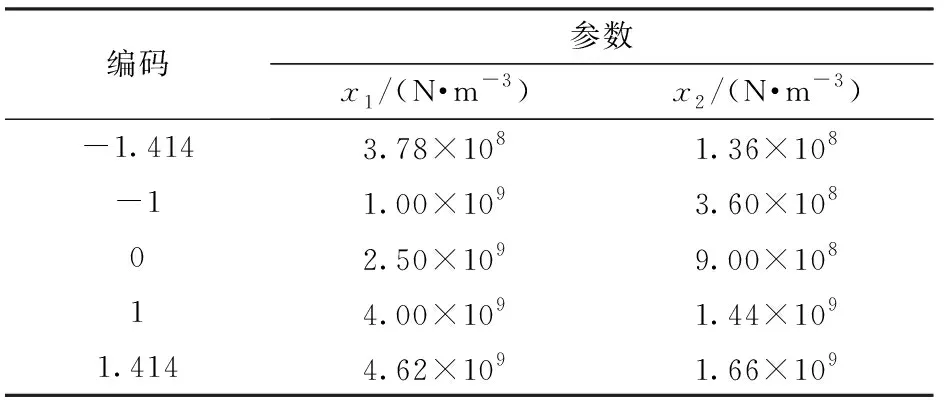
表5 粘结模型参数编码Tab.5 Coding of bonding parameters
2 结果与分析
2.1 休止角参数标定试验
2.1.1休止角影响参数筛选
将影响休止角的基本接触参数A~F作为试验因素,进行二水平因子试验设计,试验水平设置与仿真结果如表6所示。
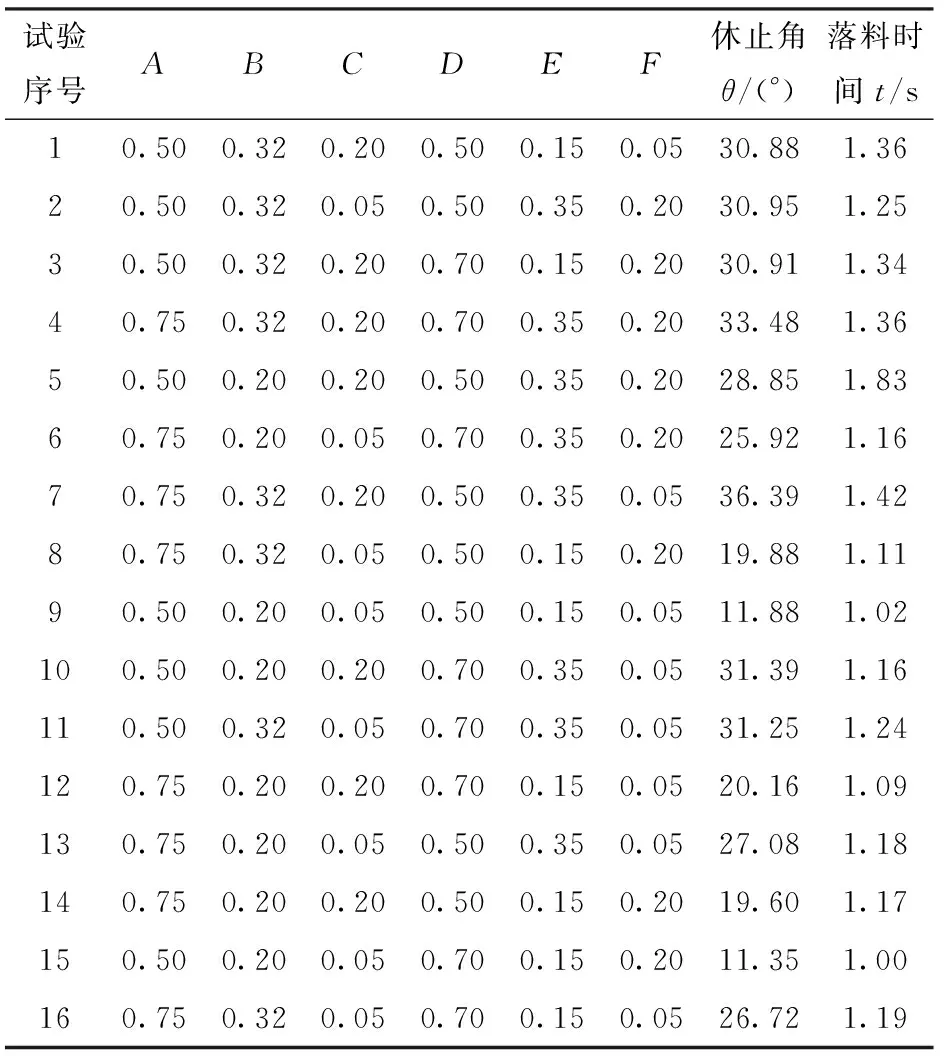
表6 休止角二水平因子试验设计与结果Tab.6 Two-level factorial design and results of angle of repose
采用方差分析方法对各个参数显著性进行检验,结果如表7所示。
由表7可知,根据影响率进行显著性排序,在颗粒饲料休止角试验中,B、C、E对休止角有显著影响,其余参数影响极小。因此,选取B、C、E作为后续试验的优化参数。无显著影响参数A、D、F取中间值,即A取0.625,D取0.60,F取0.125。
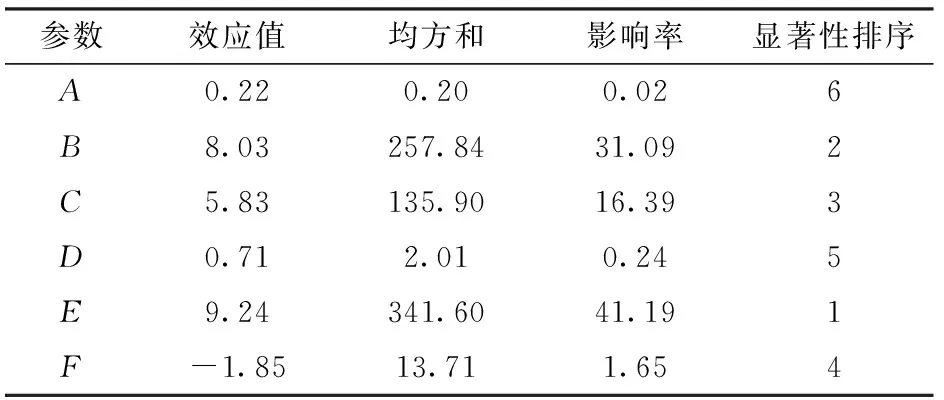
表7 休止角试验参数显著性分析Tab.7 Analysis of parameter significance in angle of repose test
2.1.2最陡爬坡试验
由上述二水平因子试验可知,B、C、E对休止角的效应为正值,即休止角随参数的增大而增大,故进行最陡爬坡试验设计,以各仿真试验所得休止角与实际休止角的相对误差为参照,进一步确定最优参数取值区间,试验设计与结果如表8所示。
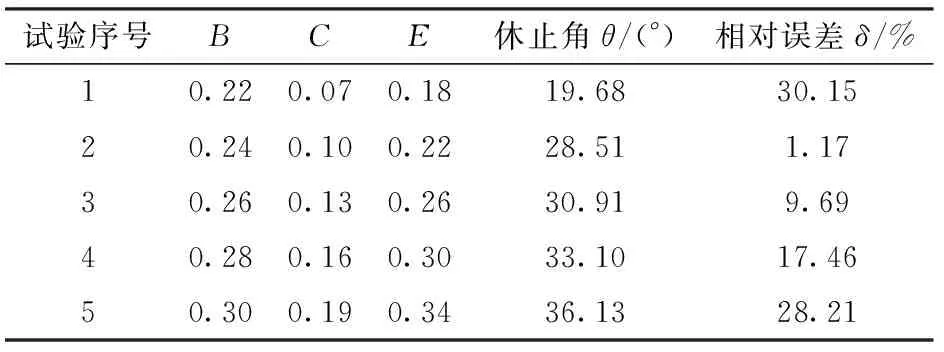
表8 休止角最陡爬坡试验设计与结果Tab.8 Experimental results in the steepest ascent test of angle of repose
随着B、C、E的逐渐增大,休止角仿真值也逐渐增大,与休止角实际值的相对误差呈先减小后增大的趋势。其中,第2组试验相对误差最小,故以第2组试验为后续试验的中心点,第1组和第3组试验分别为低水平和高水平进行后续响应面试验设计。
2.1.3响应面试验
根据最陡爬坡试验所得参数取值范围,结合BBD原理,利用Design-Expert软件进行三因素三水平响应面试验设计,中心水平设置5组重复,总共进行17组颗粒饲料休止角仿真试验。试验因素、因素水平及试验结果如表9所示。
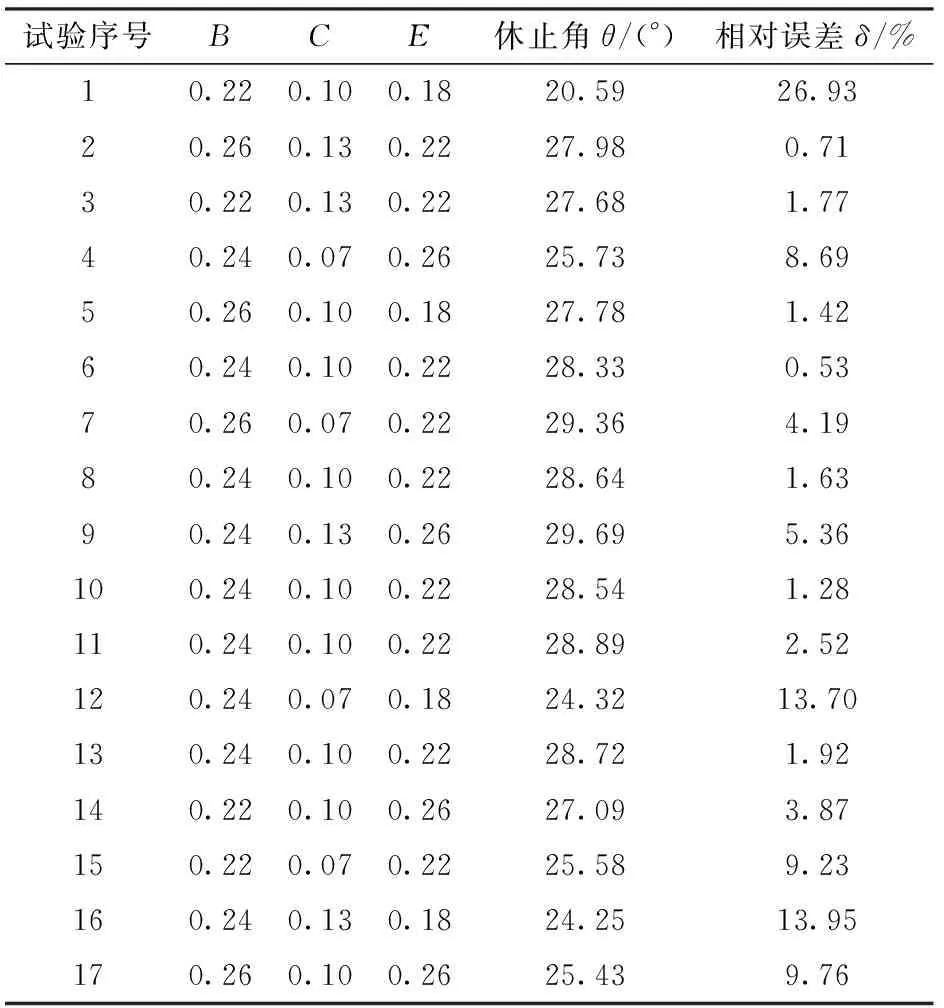
表9 休止角响应面试验设计与结果Tab.9 Design and results of response surface test of angle of repose
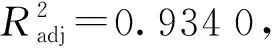
θ=28.62+1.2B+0.58C+1.38E-0.87BC-
2.21BE+1.01CE-0.87B2-0.1C2-2.53E2
(2)
求解二次回归方程(式(2)),使目标值为实际测量休止角,即28.18°,得B、C、E分别为0.23、0.12、0.22。为验证最优参数组合的可行性与准确性,采用上述参数进行仿真试验,5次重复试验测得颗粒饲料平均休止角分别为27.64°、27.86°、28.40°、28.39°、28.13°,平均值为28.08°,与实际测量休止角28.18°相对误差为0.35%,模拟结果与试验结果接近,表明试验所得颗粒饲料基本接触参数可用于模拟实际情况。
2.2 碰撞恢复系数标定试验
由预仿真试验可知,参数A取值范围为0.50~0.75,参数D取值范围为0.55~0.70,故分别取A为0.50、0.55、0.60、0.65、0.70、0.75进行饲料间碰撞恢复系数标定,分别取D为0.55、0.60、0.65、0.70进行饲料-软PVC间碰撞恢复系数标定,其余参数保持恒定,即饲料间静摩擦因数0.23、饲料间滚动摩擦因数0.12、饲料-软PVC间静摩擦因数0.22、饲料-软PVC间滚动摩擦因数0.125。仿真试验结果如表10所示。
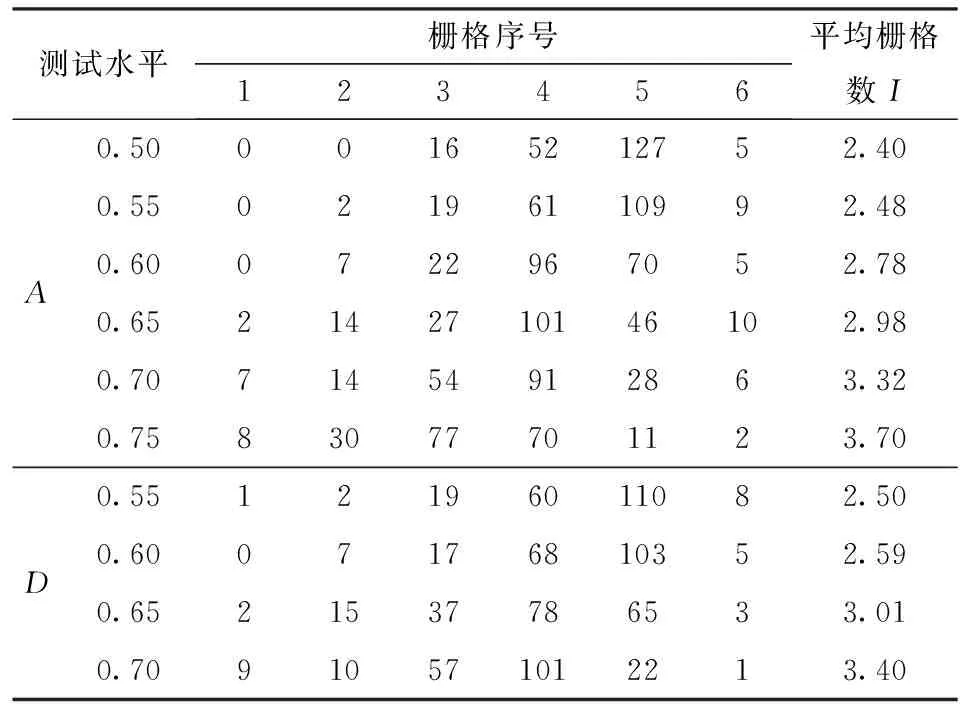
表10 碰撞恢复系数仿真试验结果Tab.10 Simulation test results of coefficient of restitution
分别以平均栅格数2.65、3.31为目标值,采用Design-Expert软件进行回归分析,得出A、D取值分别为0.58、0.69。分别以A=0.58、D=0.69进行试验验证,求得平均栅格数分别为2.62、3.29。将仿真结果与物理试验测量结果进行比较,如图7所示。
由图7a可知,参数A标定试验的仿真值与试验值的趋势基本吻合。但仿真中栅格2的颗粒数量略小于试验中栅格2的颗粒数量,仿真中栅格3的颗
粒数量略大于试验中栅格3的颗粒数量。这可能是因为在实际试验中,由颗粒粘结而形成的碰撞板上存在一定的粘结缝隙,故经释放管下落的颗粒与缝隙进行碰撞会导致颗粒碰撞后的动能降低,从而落在栅格2中的颗粒数量相对增加,而仿真中粘结缝隙少于实际试验,故落在栅格3中的颗粒会相应增加。由图7b可知,参数D标定试验的仿真值与试验值的趋势基本一致。但仿真中栅格3、4的颗粒数量与试验中栅格3、4的颗粒数量存在一定的差异,这可能是因为大多数颗粒最终下落位置靠近栅格3和4间的隔板处,当颗粒在接收盘中与隔板碰撞时会产生反弹现象,使得颗粒的运动趋势产生变化,从而影响颗粒最终的停留位置。
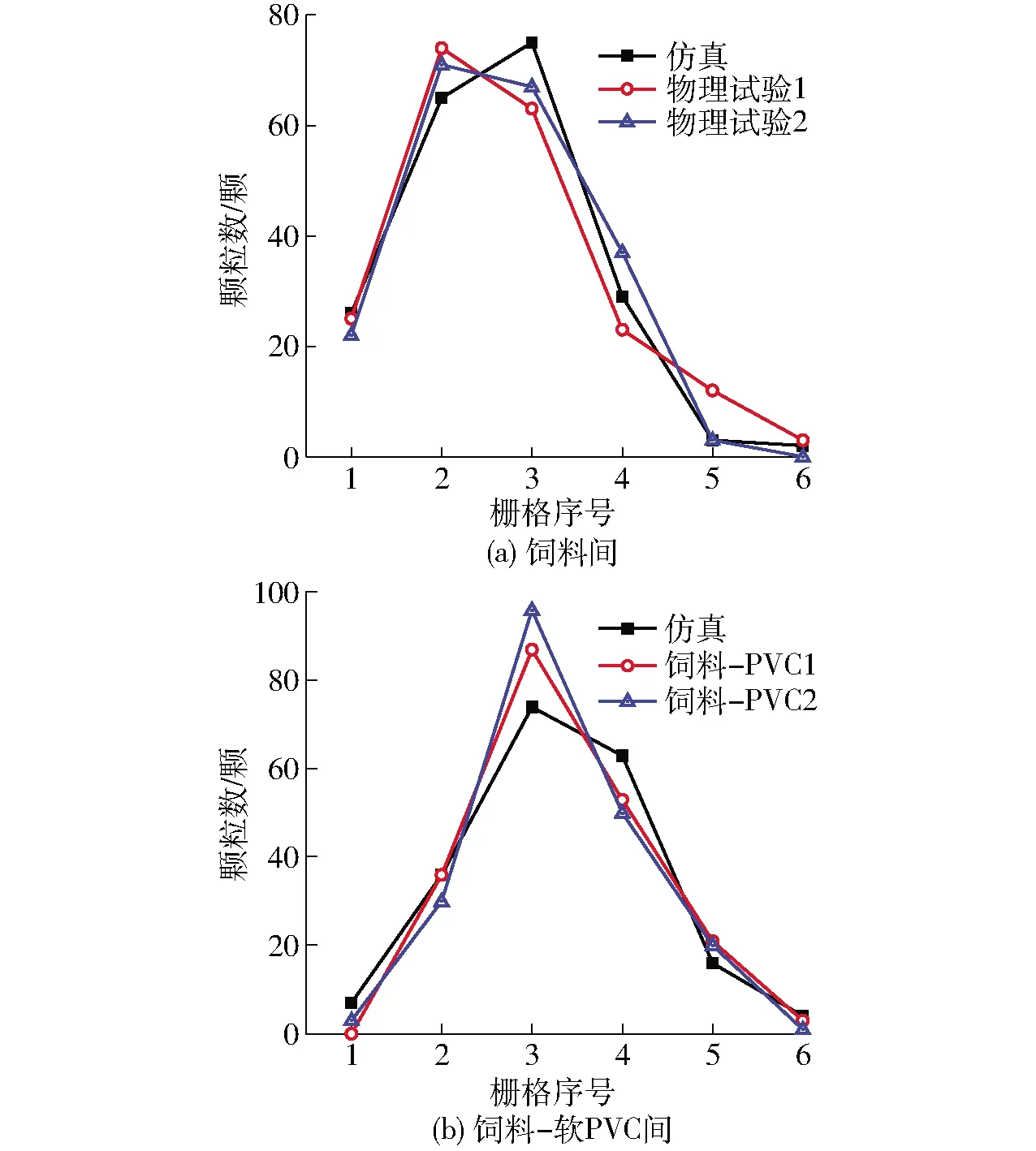
图7 碰撞恢复系数标定结果Fig.7 Calibration results of coefficient of restitution
虽然仿真与试验中各栅格颗粒数量存在一定的差异,但是整体趋势以及平均栅格数基本相同,故认为标定的颗粒饲料间碰撞恢复系数、颗粒饲料-软PVC间碰撞恢复系数可靠。
2.3 滚动摩擦因数标定试验
由上文可知,颗粒饲料标定参数A为0.58、B为0.23、C为0.12、D为0.69、E为0.22。为了保证标定参数的准确性,有必要确定F取0.125的合理性。根据表6分析可知,F对休止角试验中的落料时间有显著影响,故可以通过实际落料时间标定参数F。由休止角物理试验可知,颗粒饲料的平均落料时间为1.26 s。
根据前文所得参数F取值范围0.05~0.20,设置水平0.06、0.08、0.10、0.12、0.14、0.16、0.18、0.20进行休止角仿真试验,所得落料时间如表11所示。由表11可知,当F=0.18时。落料时间为1.23 s,与实际落料时间相对误差为2.81%,故确定0.18为颗粒与PVC材料间的滚动摩擦因数。

表11 滚动摩擦因数标定试验设计与结果Tab.11 Experimental design and results of calibration for coefficient of rolling friction
综上所述,可以获得标定后颗粒饲料间、颗粒饲料与PVC材料间的接触参数A~F依次为0.58、0.23、0.12、0.69、0.22、0.18。
2.4 粘结参数标定试验
为确定合适的粘结参数组合,根据中心组合设计原理,结合表5中参数取值范围进行响应面试验设计。根据参数取值范围,进行颗粒饲料压缩破坏仿真试验,中心水平设置5组重复,总共进行13组仿真试验。试验设计与仿真结果如表12(表中X1、X2为x1、x2的编码值)所示。

表12 粘结参数响应面试验设计与结果Tab.12 Response surface test design and results of bonding parameters
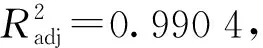
f=40.12+11.12X1+11.22X2+1.60X1X2-
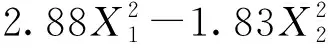
(3)
求解二次回归方程(式(3)),使目标值为实际测量破碎力,即36.22 N,结合法向刚度与切向刚度关系[31],得x1、x2分别为2.25×109、8.05×108N/m3。为验证最优参数组合的可行性与准确性,采用1.3.3节中已建立的仿真模型和颗粒模型进行单轴压缩破碎仿真试验,具体步骤如下:初始状态时,压头底部距颗粒模型顶部10 mm;在EDEM软件中对压头进行线性运动设置,为减少仿真时间,在接触颗粒模型之前,压缩速度设置为60 mm/min,在接触颗粒模型之后,压缩速度设置为10 mm/min;对压头的运动时间进行设置,使得压头总位移为13 mm;通过后处理界面,获取压头上力的最大值即为颗粒饲料的破碎力。5次重复试验获得颗粒饲料破碎力分别为36.50、37.10、36.70、37.00、36.40 N,平均值为36.74 N,与实际测量破碎力36.22 N相对误差为1.43%,模拟结果与试验结果接近,表明标定参数有效。
2.5 颗粒饲料破损模型验证
为了探究多球模型标定参数应用于粘结模型的可行性,分别使用多球模型和粘结模型开展如图8所示的单颗粒自由落料试验、斜面滑动试验和斜面滚动试验,通过对比多球模型和粘结模型的运动状态以表征各接触参数的差异。

图8 两种颗粒模型对比验证Fig.8 Comparison and validation of two particle model
针对自由落料试验,通过颗粒与底板第1次碰撞后的最大势能与初始势能之比以表征碰撞恢复系数;针对斜面滑动试验和滚动试验,设置斜面从水平位置以恒定角速度开始转动,通过记录饲料开始滑动和滚动的时间以表征静摩擦因数和滚动摩擦因数,所得结果如表13、14所示。
由表13可得,两种模型表征参数A的结果分别为0.91、0.94,相对误差为3.20%;表征参数D的结果分别为0.91、0.92,相对误差为1.10%。
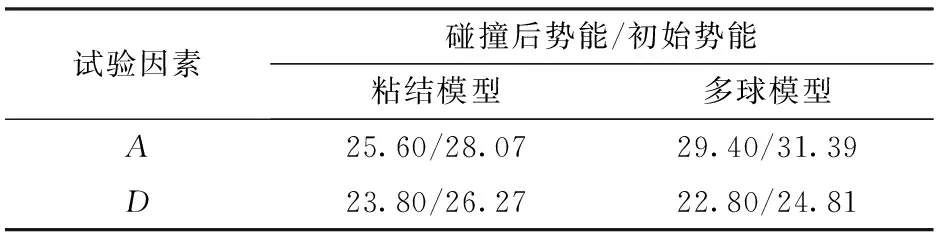
表13 不同颗粒模型自由落料试验结果Tab.13 Experimental results of free fall with different particle models μJ
由表14可得,两种模型表征参数B的结果分别为1.14、1.15 s,相对误差为0.87%;表征参数E的结果分别为1.12、1.14 s,相对误差为1.70%;表征参数C的结果分别为1.15、1.17 s,相对误差为1.71%;表征参数F的结果分别为1.11、1.12 s,相对误差为0.89%。
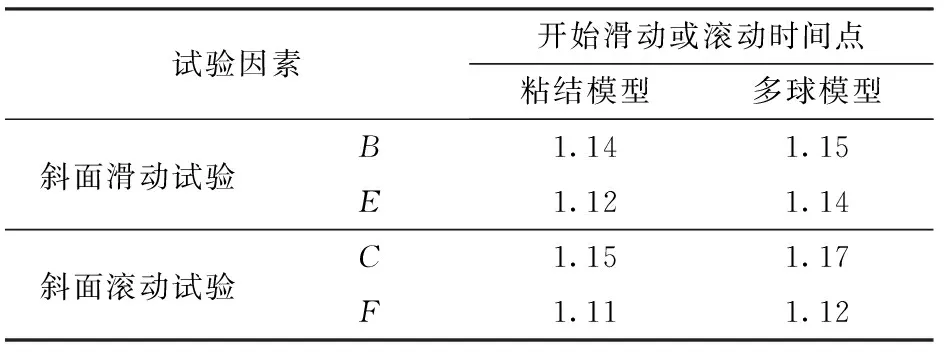
表14 不同颗粒模型斜面滑动和滚动试验结果Tab.14 Experimental results of inclined sliding and rolling of different particle models s
由试验结果对比可得,粘结模型与多球模型的运动状态基本一致,故将多球模型的接触参数运用在粘结模型上是合理的。
3 结论
(1)通过试验测定,获得试验样品颗粒饲料平均直径为2.67 mm、平均长度为8.89 mm,密度为 1 086.15 kg/m3,弹性模量、泊松比平均值分别为245.94 MPa、0.387;基于休止角试验并结合图像处理方法获得颗粒饲料休止角平均值为28.18°,通过单轴压缩破碎试验获得颗粒饲料破碎力平均值为36.22 N。
(2)通过休止角仿真试验,采取二水平因子试验、最陡爬坡试验和响应面试验等方法,标定对休止角影响显著的参数,即饲料间静摩擦因数0.23、饲料间滚动摩擦因数0.12、饲料-软PVC间静摩擦因数0.22,利用所得参数进行休止角仿真试验,仿真结果与实测值相对误差0.35%;通过碰撞恢复系数标定试验,完成饲料间碰撞恢复系数和饲料-软PVC间碰撞恢复系数的标定,分别为0.58、0.69;基于休止角仿真试验的落料时间与实际试验中的落料时间对比,完成了饲料-软PVC间滚动摩擦因数的标定,即0.18。
(3)为了考虑饲料破损问题,建立了颗粒饲料粘结模型,根据CCD原理,建立了粘结参数与破碎力之间的回归模型,由方差分析可知,单位面积法向接触刚度和单位面积切向接触刚度及其平方项、交互项对破碎力影响显著。以实测破碎力36.22 N为目标值进行参数寻优,获得单位面积法向刚度、单位面积切向刚度、临界法向应力和临界切向应力分别为2.25×109N/m3、8.05×108N/m3、455 MPa和305 MPa,利用所得参数进行单轴压缩仿真试验,所得结果与实际值相对误差为1.43%。
(4)通过仿真模拟单颗粒自由落料、斜面滑动和斜面滚动试验,对比粘结模型和多球模型的运动状态,结果表明,接触参数相同的粘结模型和多球模型运动状态基本一致,故可认为将多球模型接触参数运用至粘结模型是合理的。
